基于锥形刀具的螺旋锥齿轮齿顶倒棱加工仿真研究

卞博，洪荣晶

南京工业大学 机械与动力工程学院，江苏 南京 211800

0 引言

螺旋锥齿轮因承载力高、传动平稳，被广泛应用于飞机、车辆、工程机械等传动系统中[1-2].螺旋锥齿轮在切削加工过程中，齿面和齿顶常常会有毛刺、飞边等“棱”出现，在剧烈工况下，会产生噪声、冲击及齿面快速疲劳破坏等现象[3-5]，因此对齿顶倒棱技术的研究非常重要.

发达工业国家在齿轮倒棱技术上有较为成熟的经验，SAMPUTENSILI公司生产的SM2TA挤棱机以挤棱工艺加工热前未淬硬齿轮的齿廓棱线部分；日本山阳研制的五轴双曲面齿轮倒棱机，自动化程度较高且易操作[6]；K.M.Ribbeck等[7]在刀盘上安装多把刀具，通过刀盘与工件旋转完成螺旋锥齿轮的倒棱加工.国内部分学者对倒棱问题也进行了研究，徐彦伟等[8]提出了采用锥形砂轮实现弧齿锥齿轮大轮齿顶倒棱；李佳等[9]提出了旋分倒棱技术，该方法需要1个平移和3个旋转运动联动；魏巍等[10]提出的盘形刀具的弧齿锥齿轮齿顶倒棱加工方法，可同时加工两边倒棱，但形状误差较大，达0.5 mm.刘景成[11]提出采用盘状铣刀的弧齿锥齿轮单边倒棱加工方法，加工精度可达0.07 mm，但该方法仅适用于大轮.上述研究大多以双边倒棱为基础，着重提高倒棱效率，对于倒棱精度的重视不够.鉴于此，本文拟以小轮为对象，提出基于锥形刀具的螺旋锥齿轮齿顶倒棱加工方法，即通过建立齿顶棱线方程，设置倒棱参数，对锥形刀具轨迹进行求解计算，从而实现倒棱大小的灵活控制，同时提高倒棱精度.

1 齿顶棱线方程的建立

1.1 锥形刀具倒棱加工原理

螺旋锥齿轮形体复杂，但根据成型原理，可将螺旋锥齿轮看作是由一个个齿形截面(见图1)衔接构成的，所有截面均垂直于齿向曲线，因为齿顶棱线依据齿向线生成，所以这些截面近似垂直于齿顶棱线.

锥形刀具倒棱加工，实质上是指刀具切削侧刃沿齿顶做切削运动的加工.锥形刀具在进行倒棱加工时，刀具走向与齿顶棱线密切相关，其轨迹求解流程为：根据垂直于齿顶棱线的齿形截面对倒棱参数进行计算，得出刀具倒棱加工轨迹.因计算的需要，应首先对齿顶棱线方程[12]进行求解.

1.2 齿顶棱线方程的推导

本文以一对螺旋锥齿轮副的小轮为例来研究倒棱加工.由文献[13]可知，其齿顶棱线方程为

图1 齿形截面Fig.1 Tooth section

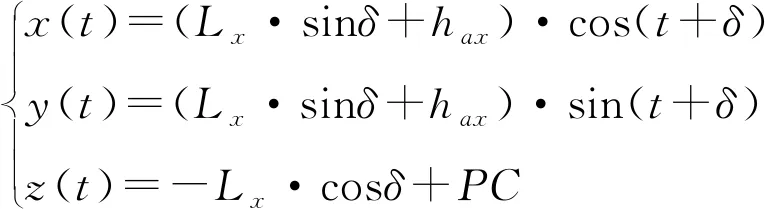
①

其中，Lx为齿线上任一点锥距，hax为棱线任一点齿顶高，δ为节锥角，t为齿线任一点转角，PC为节锥顶点与顶锥顶点的距离.

1.3 齿顶棱线方程的验证

取一对螺旋锥齿轮副的小轮参数并创建模型，进行齿顶棱线和后续倒棱的计算和验证.螺旋锥齿轮参数分别为：齿数15，大端模数6，外锥距95.29 mm，节锥角28.18°，压力角20°，螺旋角39.87°，齿顶高4.2 mm，齿根高5.4 mm.在UG中根据基本参数构建的螺旋锥齿轮三维模型如图2所示.

提取三维模型中一条齿顶棱线的30个点(即图2所示模型上的棱线点集)，在Matlab中与式①齿顶线方程进行比对，齿顶棱线方程验证结果如图3所示.由图3可以看出，齿顶棱线方程与三维模型中棱线提取的数据点基本重合，说明螺旋锥齿轮齿顶棱线参数方程与理论模型误差不大，可以作为后续刀具轨迹计算的依据.

2 刀具轨迹求解

2.1 局部坐标系原点与各轴矢量计算

将齿轮轴心线与坐标轴重合，使得给定主坐标系位于螺旋锥齿轮上顶部中心，且Z轴与轴心线一致.根据齿顶棱线分割的离散点，得出与离散点相同数量的棱线法平面，设离散点为O2(x0,y0,z0),对应齿顶棱线方程自变量t0，棱线法平面为P，则法平面方程[14]为

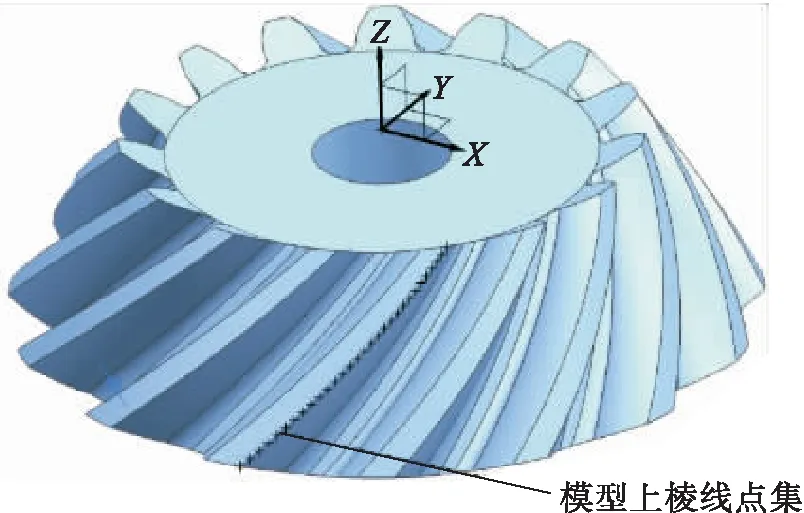
图2 螺旋锥齿轮三维模型Fig.2 3D model of spiral bevel gear

x′(t0)·(x-x0)+y′(t0)·(y-y0)+
z′(t0)·(z-z0)=0

该法平面的法矢量v2=[x′(t0),y′(t0),z′(t0)]为局部坐标系的Y坐标轴矢量，法截面P与Z轴交点及矢量如图4所示，其中法平面与螺旋锥齿轮轴线的交点O1即为所求的局部坐标系原点，该点在主坐标系中的坐标为O1(0,0,w)，根据平面与直线的交点关系，求得：

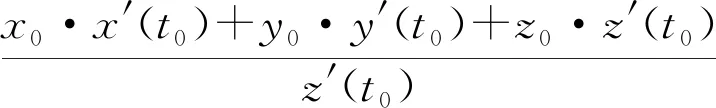
点O1与离散点连成的直线矢量作为局部坐标系的Z坐标轴矢量v3[x0,y0,z0-w]，因坐标系三矢量两两垂直，所以

因v1有无穷多解，可选取其中一个v1=[1，b,c]作为X轴矢量.

2.2 当量齿轮齿廓齿顶角度求解

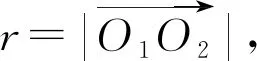
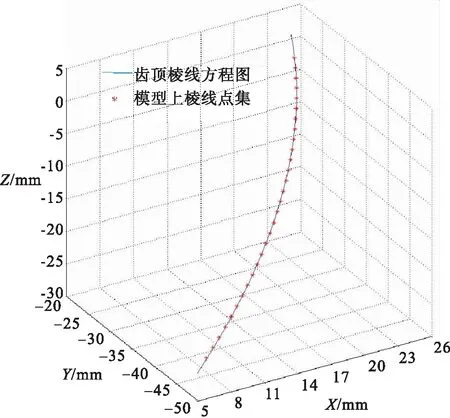
图3 齿顶棱线方程验证结果Fig.3 Verification results of tooth top ridge equation

由于当量齿轮齿廓齿顶角度θ并不是一个定值，故它会随着倒棱大小的改变而作微小改变.为提高刀具轨迹的精度，需要求解齿廓顶角θ与倒棱大小参数Ld1和Ld2之间的关系.而大多螺旋锥齿轮齿顶倒棱深度在0.2～0.5 mm之间，这远远小于齿轮的尺寸，所以齿顶倒棱形状可看作一个三角形，即弧线近似为直线，根据渐开线与圆的性质，可由螺旋锥齿轮的基本参数和给定的倒棱长度，求出齿廓顶角θ.螺旋锥齿轮当量齿轮参数如图6所示.在图6的坐标系下，齿顶角求解过程如下.

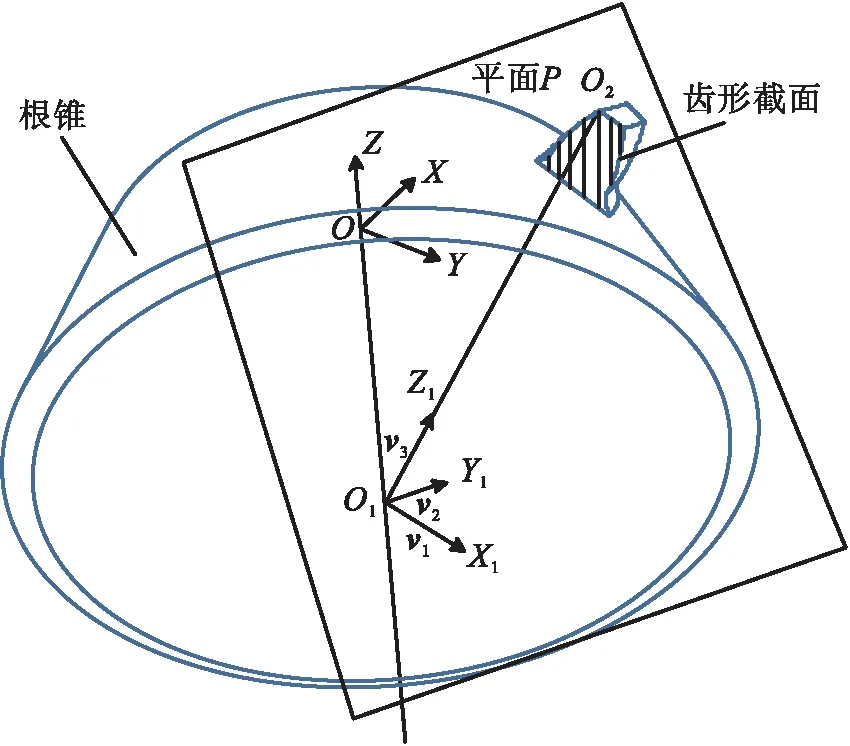
图4 法截面P与Z轴交点及矢量Fig.4 Intersection point and vector of normal section P and Z axis

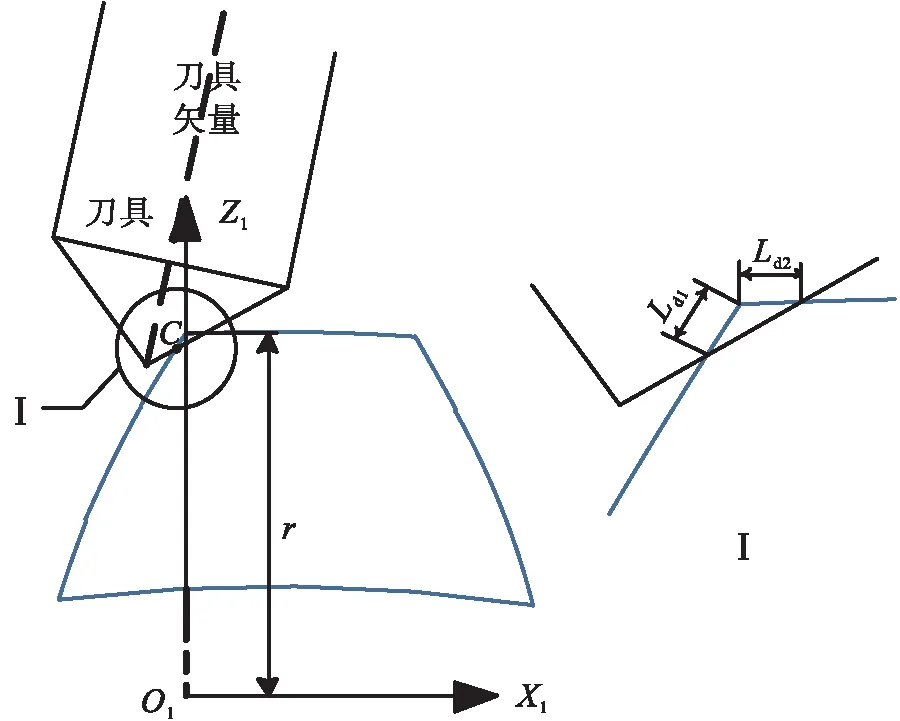
图5 单齿截面与倒棱参数Fig.5 Single tooth section and chamfer parameters

1)首先求解渐开线与齿顶圆的交点坐标，根据渐开线方程计算得O3坐标：

O3=[x3,y3]=[Rj·sinα0-Rj·α0·cosα0,Rj·cosα0+Rj·α0·sinα0]

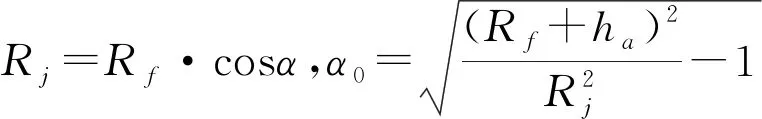
2)根据弧长Ld1和Ld2可以计算出点H和点G的坐标，计算可得

H=[xh,yh]=
[x3·cosφ-y3·sinφ,x3·sinφ+y3·cosφ]

G=[xg,yg]=
[Rj·sinσ-Rj·σ·cosσ,Rj·cosσ+Rj·σ·sinσ]

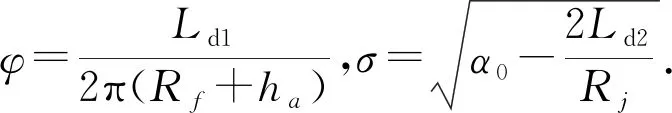
3)联立O3，H，G这3点的坐标即可求出齿顶角，即

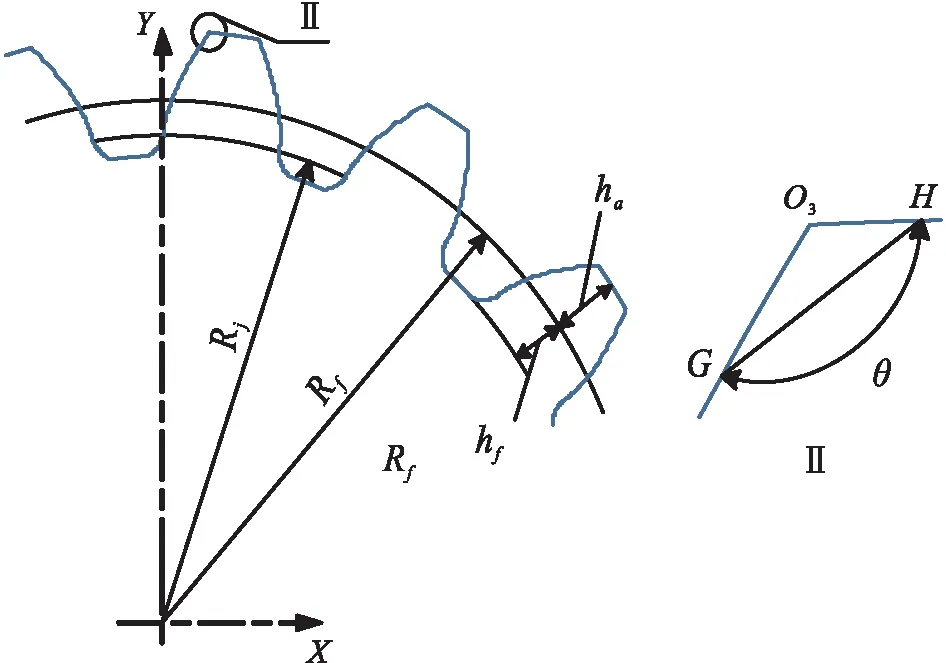
图6 螺旋锥齿轮当量齿轮参数Fig.6 Equivalent gear parameters of spiral bevel gear

②

2.3 刀位点在副坐标系的坐标求解

刀位点与刀轴矢量如图7所示，其中，O2为倒棱曲线上离散点，在副坐标系下坐标为[0,0,r]，倒棱形状可看成三角形，线段O2D可看成与X2轴平行，O2D=Ld1，O2C=Ld2，设定刀具角度为δ，刀尖露出长度BC=Lt.根据平面几何关系，求出刀位点B和刀轴矢量上A的坐标.

先求出三角形的内角：

③

据此可以求出γ角：

④

其中

⑤

根据式②—⑤，可以得出B点和A点的坐标分别为

B=[-lBE,0,r-lO2E]=
[-lBO2·sinγ,0,r-lBO2·cosγ]

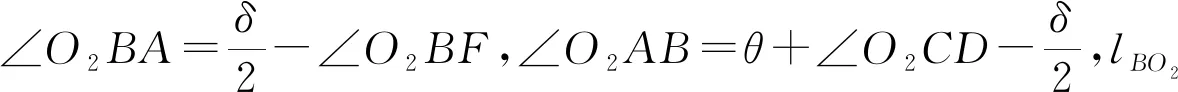
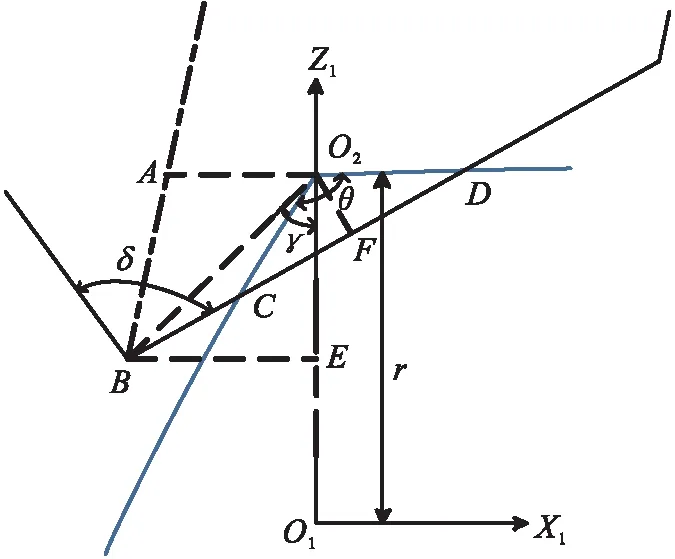
图7 刀位点与刀轴矢量Fig.7 Tool point and tool axis vector

2.4 坐标转换

将副坐标系下的刀位点坐标转换为主坐标系下的坐标，以便于生成加工代码.

首先将副坐标系各轴矢量转换为单位矢量，转换后单位矢量为v11=[ux,uy,uz]，v21=[mx,my,mz]，v31=[nx,ny,nz].设某点在主坐标系下坐标为(x,y,z)，在副坐标系下坐标为(xf,yf,zf)，副坐标系坐标原点为O1(0,0,w)，据此可以构建一个如下的线性方程组：

因此，副坐标系点转为主坐标系坐标的转换矩阵为

A，B两点在主坐标系下的坐标可由转换矩阵T求出：

AZ=T·AT

⑥

BZ=T·BT

⑦

由一个个刀尖点BZ组成刀尖轨迹.

刀轴矢量为

⑧

由式⑥—⑧即可确定刀具轨迹.

3 仿真实验与结果分析

为检验本文提出的倒棱加工方法的有效性，进行了仿真实验.通过对仿真模型数据的提取，计算出法截面和齿顶棱线与倒棱边界线交点之间的距离，并与倒棱大小参数进行比对分析.

3.1 倒棱参数设置与仿真步骤

设置3组倒棱参数：Ld1=Ld2=0.3 mm；Ld1=0.2 mm，Ld2=0.3 mm；Ld1=0.3 mm，Ld2=0.2 mm.锥形刀具参数为Φ4×90°×50×3F，刀尖露出长度Lt=0.5 mm.在Matlab中，根据式⑥—⑧编写由齿顶棱线离散点转换为倒棱刀位点和刀轴矢量的程序，并后置处理得到数控加工代码，而后在数控机床加工仿真软件VERICUT平台上建立倒棱加工仿真模型，即可进行仿真.

在软件VERICUT中导入机床模型文件，在机床转台位置添加齿轮模型(齿轮模型参数见1.3)，并设置坐标系统csys(0，0，0).然后添加锥形刀刀具模型，刀具编号设置为1，控制点设置为刀尖，在添加数控仿真代码后，进行加工仿真.倒棱切削模型如图8所示，其中倒棱切削位置两端的曲线为倒棱边界线.将VERICUT切削模型导出，在UG中打开并提取两端倒棱仿真边界曲线.

3.2 误差评价指标与结果分析

UG中的倒棱仿真边界曲线与齿顶棱线如图9所示，其中，中间曲线为轮齿右侧齿顶棱线，两端为倒棱仿真边界曲线.在齿顶棱线上均匀分布20个离散点，以这些离散点确定齿顶棱线法平面，法平面与两端倒棱边界线相交得到

图8 倒棱切削模型Fig.8 Chamfer cutting model

位于同一法平面的点U和L.将点U与点T之间的空间距离设为齿顶距离Dd1，T点与L点之间的空间距离设为齿面距离，倒棱形状误差可由如下公式进行定义：

e=max(|Dd1-Ld1|,|Dd2-Ld2|)

根据设置的3组倒棱参数进行仿真并比对，倒棱形状误差结果如图10所示.由图10可以看出，3组不同参数的倒棱的形状误差最大值皆出现在齿顶中部，而向两端的形状误差都是呈逐渐变小的趋势，说明倒棱刀具轨迹在齿顶中部的形状误差最大，在齿顶上下两端的形状误差最小；3组倒棱形状误差均不大，最大形状误差≤0.05 mm，远小于文献[10-11]的误差，说明锥形刀具倒棱确实提高了倒棱精度，且在刀位点和刀轴矢量方程中调整倒棱大小参数可灵活控制倒棱大小.本文方法中锥形刀具强度高、寿命长，具有成本低、耐用度高的优点，且该方法可在通用五轴机床上实现，无需专用机床，加工灵活性较高.

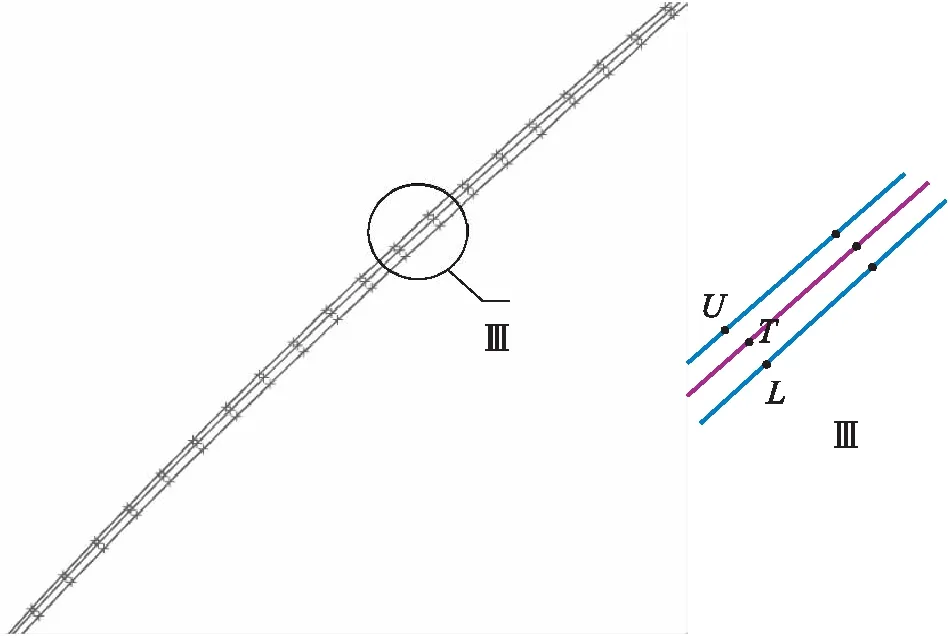
图9 倒棱仿真边界曲线与齿顶棱线Fig.9 Chamfer simulation boundary line and tooth crest line

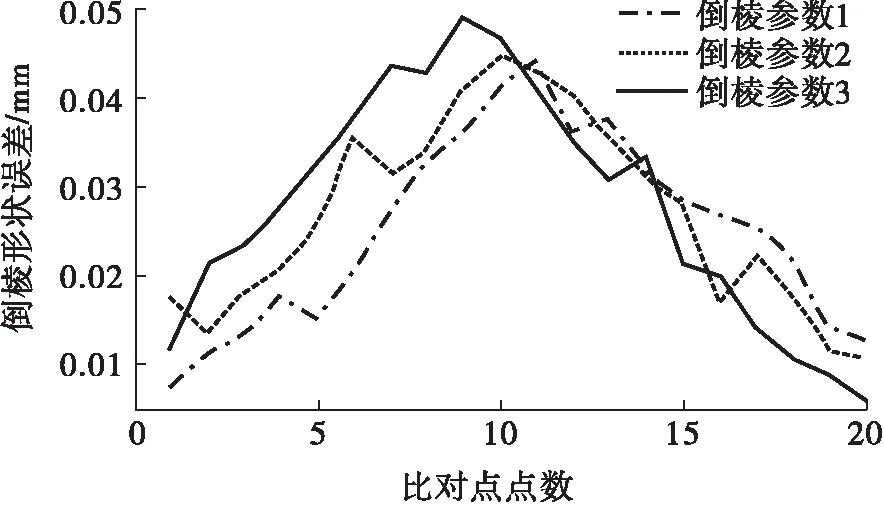
图10 倒棱形状误差结果Fig.10 Result of chamfer shape error

4 结语

本文提出基于锥形刀具的螺旋锥齿轮齿顶倒棱加工方法，根据齿顶棱线方程和倒棱参数的设置，对锥形刀具的刀位点和刀轴矢量进行了公式推导，进而求解刀具加工轨迹.仿真结果表明，在3组不同倒棱参数下，倒棱的形状误差不超过 0.05 mm，切实提高了倒棱精度，且倒棱大小可根据刀具轨迹方程进行调整，验证了本文倒棱方法控制倒棱大小的精确性和灵活性.本文以小轮为研究对象，补足了单边倒棱只研究大轮而忽视小轮的不足，得出的倒棱加工刀位计算公式，为下一步倒棱自动编码软件的开发提供了理论依据.