考虑附属管的实尺寸钻井隔水管系统涡激振动二维数值模拟研究
孔腾腾,王嘉松,吴文波,许亮斌,盛磊祥,李朝玮
(1. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240; 2. 广州大学 机械与电气工程学院,广州 510006;3. 中海油研究总院有限责任公司,北京 100028)
涡激振动(vortex-induced vibration, VIV)是一种流体与固体相互作用耦合的现象。当流体流经非流线型钝体时会在钝体后方发生分离,并产生交替泄放的漩涡。周期性的漩涡脱落会产生作用于钝体的周期性变化的升阻力,诱发钝体振动,即涡激振动。当涡脱频率和振动频率与结构的固有频率相近时,会引发结构的大幅值振动,即共振,导致结构的疲劳损坏和结构失效,严重威胁生产生活安全。
许多学者将目光投向了双圆柱和多圆柱的涡激振动问题。Zhao等[1-2]研究了串列和并列刚性连接双圆柱在低雷诺数下的涡激振动响应。在串列圆柱中,太大或太小的间距将导致圆柱的锁定区增大或减小,但圆柱系统的振幅均大于单圆柱的振幅。在并列圆柱中,圆柱系统的锁定区比单圆柱的锁定区更小,且涡激振动和驰振将同时出现在圆柱的响应中。Zhao等[3]研究了2个不同直径圆柱错列排布时的涡激振动特征,讨论了圆柱间隙和来流攻角对涡激振动锁定区的影响。Zhao等[4]采用有限单元法研究了正方形排布的四圆柱双自由度涡激振动,研究发现来流攻角对四圆柱系统的振动响应影响很大。Zhu等[5-6]采用SST(shear stress transfer)k-ω湍流模型研究了控制杆对圆柱系统涡激振动的影响,讨论了雷诺数、控制杆位置角、旋转速度、数量、直径比、间隙比对主圆柱上流体力和涡激振动响应的影响。Song等[7]研究了来流攻角和间隙比对附有3根控制杆的多圆柱系统涡激振动响应的影响。结果表明,在来流攻角为45°、间隙比为0.9时的抑制效果最好。田启龙等[8]采用离散涡方法对均匀布置4~10根等直径附属管的隔水管系统的涡激振动进行了数值模拟研究。结果表明,附加附属管后隔水管与裸管相比受力系数与振幅均有不同程度的减小,对隔水管涡激振动的抑制效果明显。不同数量的附属管对来流攻角的敏感性也各不相同,其中附加10根附属管对涡激振动的抑制效果最好。Wu等[9]采用二次开发的OpenFOAM程序对主圆柱后刚性连接一根小控制杆的隔水管系统在低雷诺数下的涡激振动进行了数值模拟研究。结果表明,间隙比越小可以激发更大范围的锁定状态,并且可以观察到更高阶的次谐波共振。控制杆在小间隙比时对隔水管系统的涡激振动产生很大影响甚至起决定性作用。随着间隙比的增加,控制杆的作用逐渐变弱。Silva-ortega等[10]通过水中试验研究了在主圆柱周围环形均匀刚性连接2根、4根和8根控制杆的多圆柱系统,讨论直径比和间隙比对多圆柱系统涡激振动的影响。结果表明,在多数布置下控制杆能抑制涡激振动,但在一些情况下会产生类似于驰振的响应,布置8根控制杆时抑制效果最好。Jiménez-gonzález等[11]对下游刚性连接一对控制杆的多圆柱系统进行水中试验。结果表明,在所有布置下多圆柱系统的振幅均有所减小,尤其在直径比为0.4D时振幅的抑制效果达到90%以上。Gao等[12]对低雷诺数下弹性连接的正方形排布四圆柱系统进行了数值模拟,研究了来流攻角为0°~45°、约化速度为3~14的涡激振动响应和尾涡模式。结果表明,来流攻角对涡激振动幅值和力系数均有显著影响,尤其是对下游圆柱影响更为明显。Huera-huarte等[13]试验研究了固定圆心间距为1.3D时,串列刚性连接单一控制杆的双圆柱系统的流致振动响应,在小于等于1的范围内改变下游圆柱与上游圆柱的直径比。结果表明,随着直径比的增大涡激振动响应逐渐减弱。Munir等[14]利用直接数值模拟方法对刚性连接的2个并列等直径圆柱的涡激振动响应进行研究,讨论了间距比和雷诺数对双圆柱系统涡激振动锁定区和涡脱的影响。
海洋钻井平台是深海油气资源勘探开发的主要工具,而隔水管是连接深海钻井平台与海底井口的“咽喉”。在海洋石油钻井操作中,常常需要在钻井隔水管附近布置一些附属管线,如压井管线、泥浆增压管线、化学管线等。在实际工程中为了安装操作方便及成本考虑,附属管通常直径大小不同,且不均匀地紧密布置在隔水管主管周围。隔水管附属管主要从功能上考虑其布局,而不是从流动控制或涡激振动控制角度考虑。Wu等[15]从流动控制角度开展数值模拟研究,讨论了来流攻角对多圆柱系统流体力和涡脱模式的影响。结果表明,附属管线对隔水管主管有很好的流动控制效果,但受来流攻角的显著影响,个别时候可能增大曳力,多数情况下可显著减小升阻力。然而,实际附属管线对钻井隔水管涡激振动有怎样的影响尚未有报道,但值得关注。本文以正服役于南海油气开发的某实尺寸钻井隔水管系统为模型,基于RANS(Reynolds-averaged Navier-Stokes)方程及k-ω湍流模型,采用二次开发的嵌入多圆柱运动求解模块的OpenFOAM求解器,分析了实尺寸钻井隔水管系统(含有错列圆柱、不同间隙比、不同直径比等特性)在不同来流攻角和雷诺数下的二维涡激振动响应特征。
1 数学模型
本文采用的流动控制方程为二维Navier-Stokes方程结合k-ω湍流模型,有限体积法进行离散求解。采用PIMPLE算法进行压力速度解耦。笛卡尔坐标系中黏性不可压缩流体非定常流动的控制方程的解析形式可以表示为
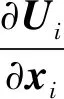
(1)
(2)
式中:U为流体的速度向量;x为空间坐标向量;μ为分子动态黏度系数;p为流体压强;ρ为流体密度;τ为雷诺应力张量。这里使用k-ω湍流模型,用Boussinesq表达式在2个方程模型中计算雷诺应力
(3)
(4)
式中:μt为湍流黏度系数;δ为克罗内克尔张量算子;k为湍动能;ω为湍流耗散率。湍流的k和ω的输运方程可表示为
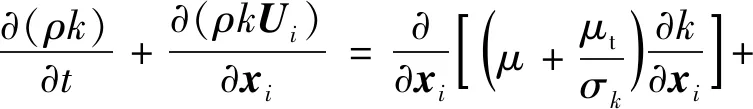
(5)
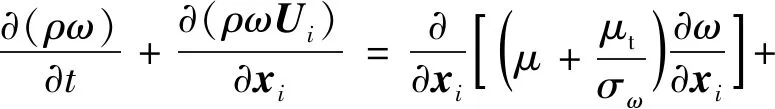
(6)
(7)
(8)
式中:S为流体的平均应变率张量;σk=2.0;σω=2.0;γ1=0.553;β1=0.075;β*=0.09; 常量取值可参见文献[16]。
考虑附属管与主管整体一起运动,结构控制方程采用单一弹簧振子模型对多圆柱同步运动系统进行模拟
(9)
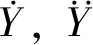
在圆柱涡激振动中,无量纲横流向均方根振幅(Yrms·D-1)的表达式为
(10)
式中:D为实尺寸钻井隔水管系统中主圆柱直径,取D=0.533 4 m;N为稳定后至少20个周期内的数据个数。
本文采用的实尺寸钻井隔水管系统的横截面示意图,如图1所示。图1表示当来流攻角为0°时的布置情况。图1中:θ为主管上的周向角;U∞为来流速度。参考实际工况中两端铰支的钻井隔水管的第一阶固有频率约为fn=0.024 4。实尺寸钻井隔水管系统中附属管的直径和几何配置参数,如表1所示。
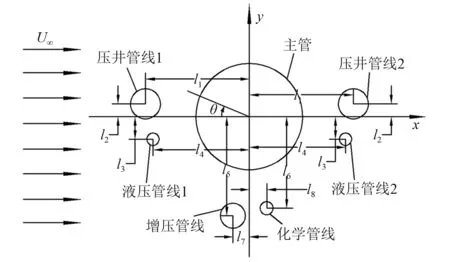
图1 实尺寸钻井隔水管系统模型示意图Fig.1 Sketch of the model for a real drilling riser system
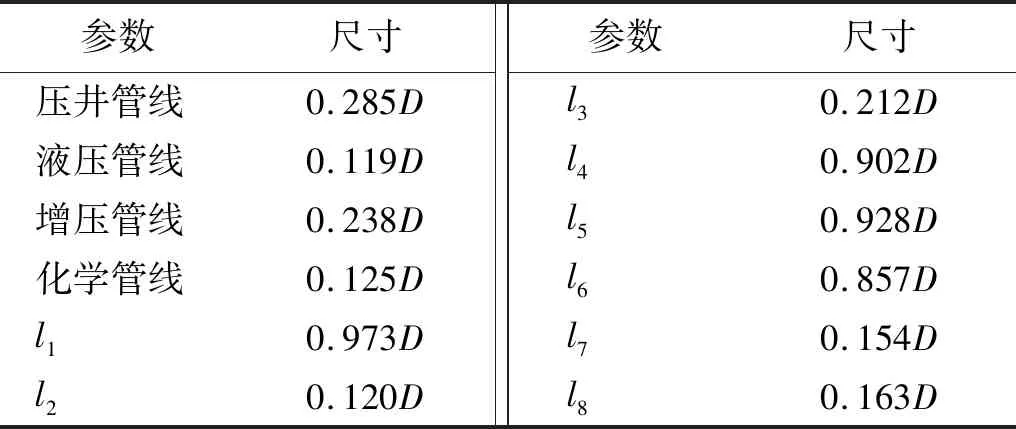
表1 实尺寸钻井隔水管系统中附属管的直径和位置参数
如图2所示,α为来流方向与x轴正方向的夹角,即来流攻角。本文所采用的实尺寸钻井隔水管系统模型可分别在顺流向和横流向振动。系统中的所有管线之间刚性连接,即隔水管与附属管线在任意时刻同步运动,且圆柱系统在两方向上的刚度系数ks和阻尼系数cs相同。海水中隔水管的质量比较小,本文取质量比为m*=3,阻尼比为ζ=5×10-4,刚度系数根据约化速度计算得到。
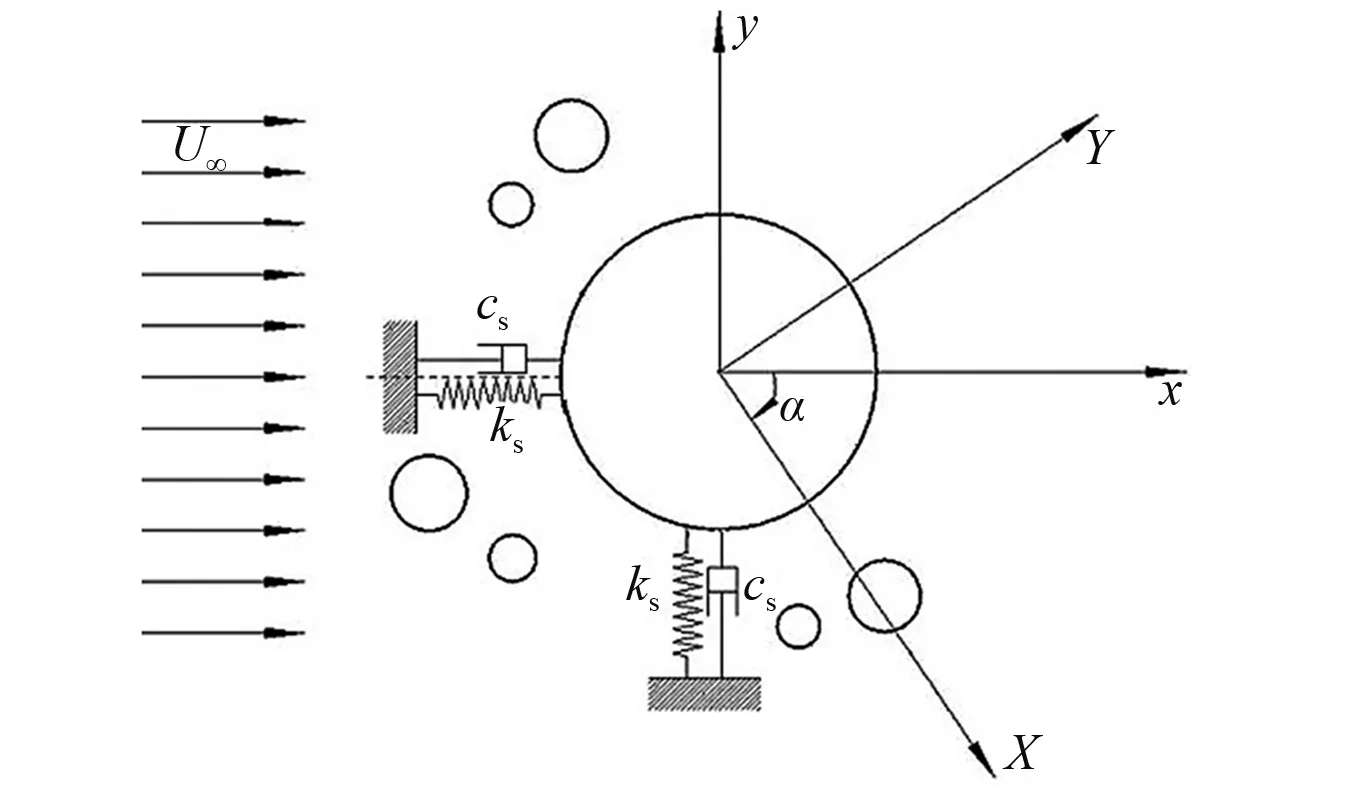
图2 实尺寸钻井隔水管系统涡激振动模型示意图Fig.2 Sketch of the model for VIV of a real drilling riser system
本文计算域选取65D×30D的矩形域,主圆柱中心距入口边界及上、下边界的距离皆为15D,距出流边界的距离为50D。采用非结构网格离散计算域,在各圆柱近表面采用贴体网格处理,且第一层网格厚度满足y+≈1,以准确模拟圆柱边界层中的流动。主圆柱周向网格数为200,各附属管为140。入口边界初始湍流强度设为1%,涡黏性系数比设为10。实尺寸钻井隔水管系统的局部网格,如图3所示。

图3 实尺寸钻井隔水管系统局部网格Fig.3 The mesh around the cylinders of a real drilling riser system
2 结果与讨论
2.1 单圆柱涡激振动数值模拟结果
为验证模型和计算方法,本文首先对Khalak等[17]的试验模型进行了数值模拟,并将数值计算结果与试验结果进行了对比,Guilmineau等[18-19]的数值工作中也采用了相同的立管响应模型参数。根据试验条件:圆柱的直径为D=0.05 m;固有频率为fn=0.5;质量比为m*=2.4;质量阻尼比为m*ζ=0.013;f为圆柱在横流方向上的振动频率。通过改变雷诺数来改变来流的约化速度,从而观测圆柱系统涡激振动随约化速度的改变。采用k-ω湍流模型进行数值模拟,入流边界上的初始湍流强度为5%。图4给出本文计算和其他数值模拟得到的涡激振动响应与试验结果的比较。
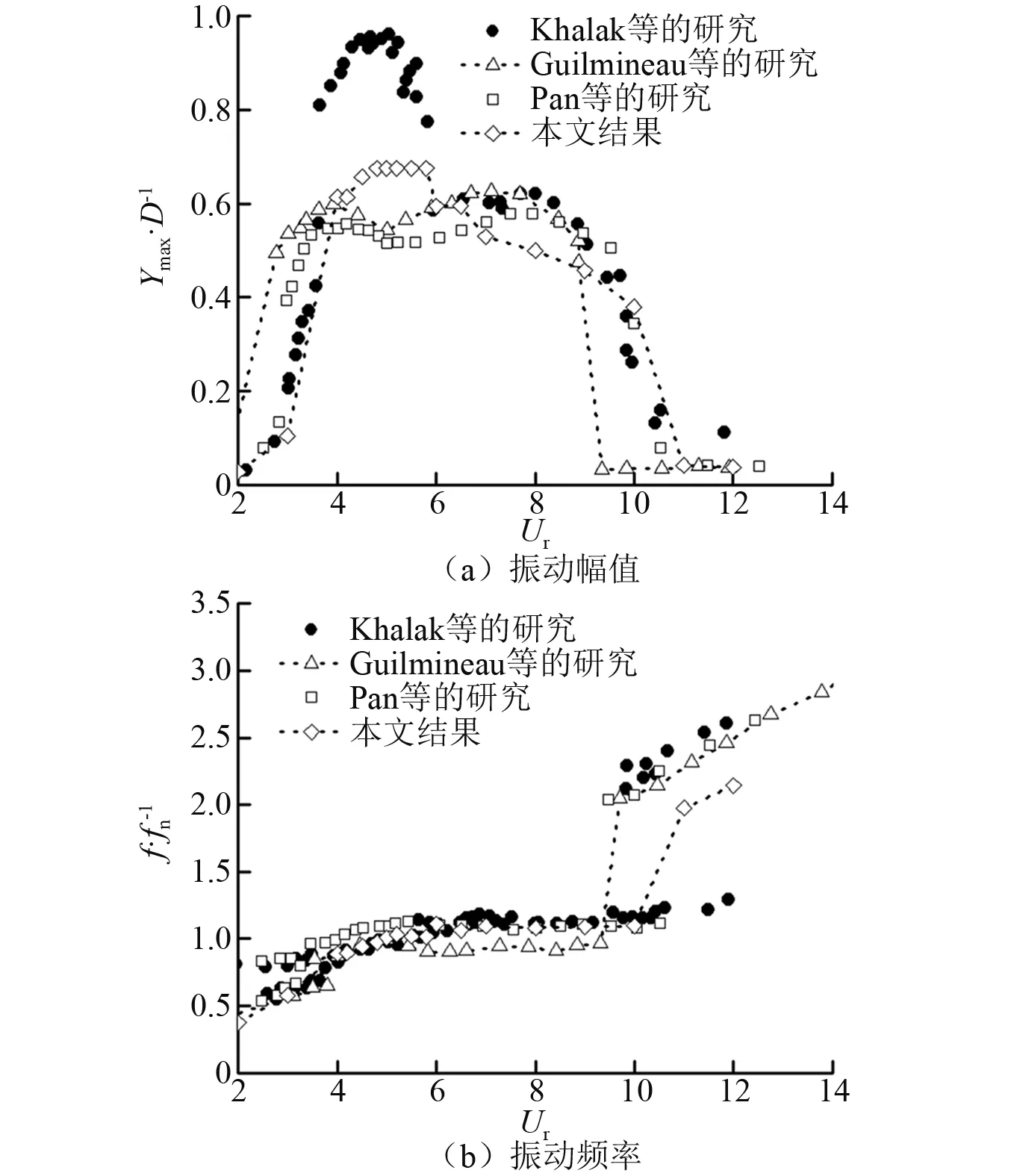
图4 高雷诺数下单圆柱涡激振动的幅值和频率Fig.4 The VIV amplitude and frequency of single circular cylinder at high Reynolds number
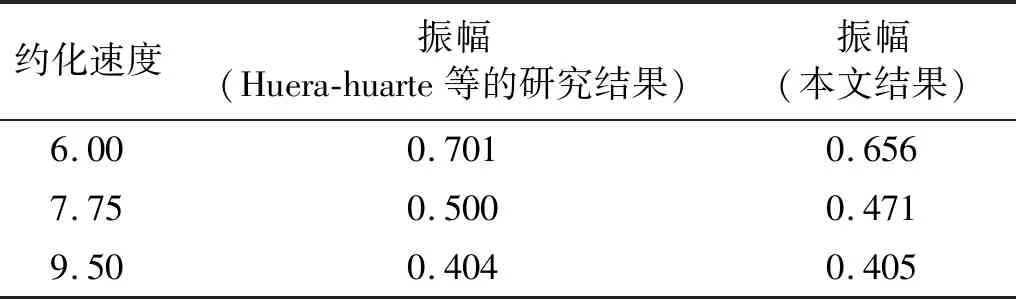
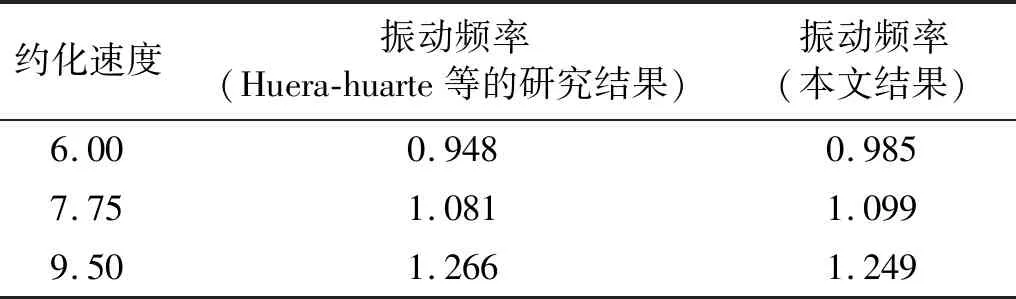
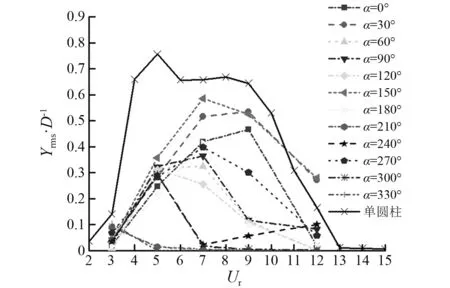
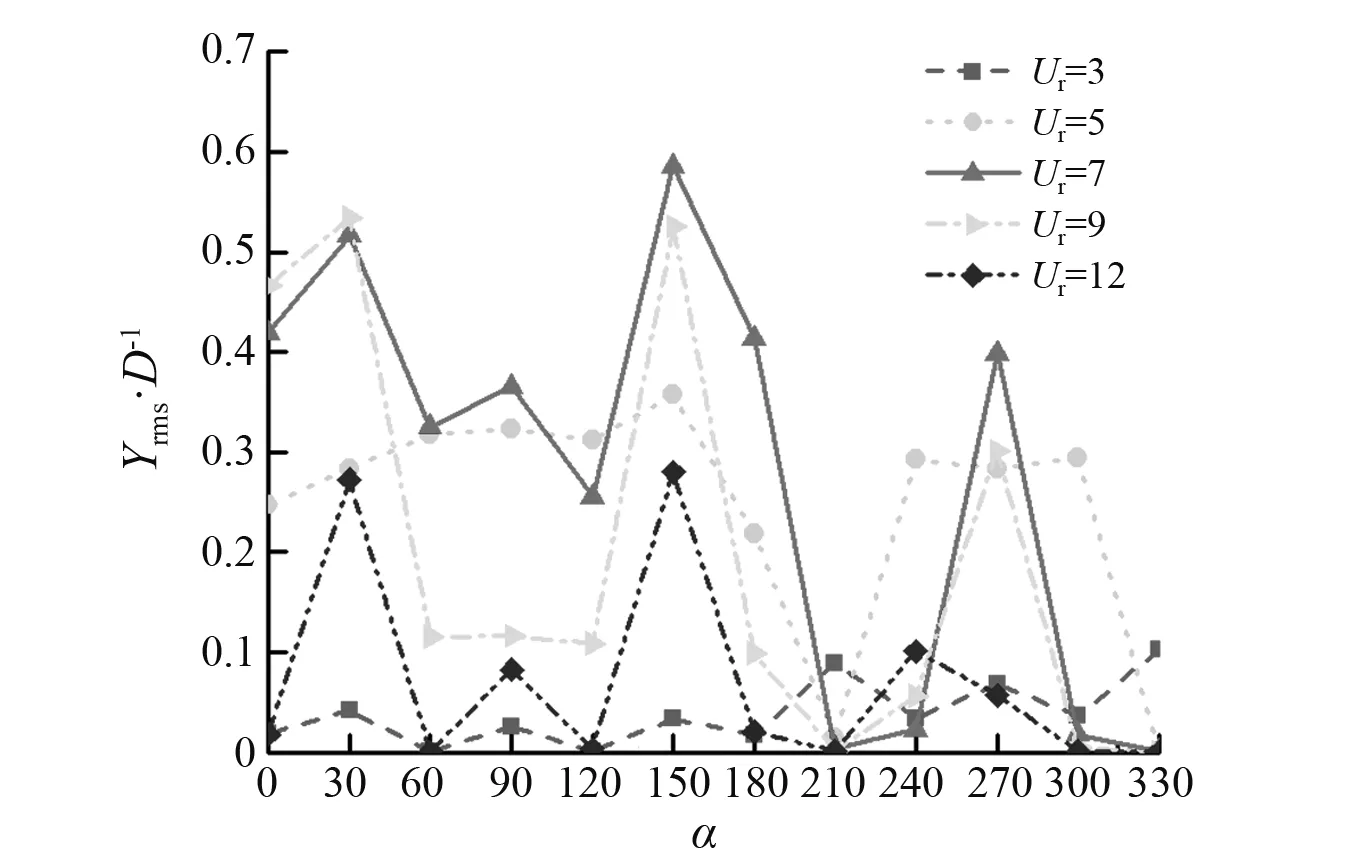
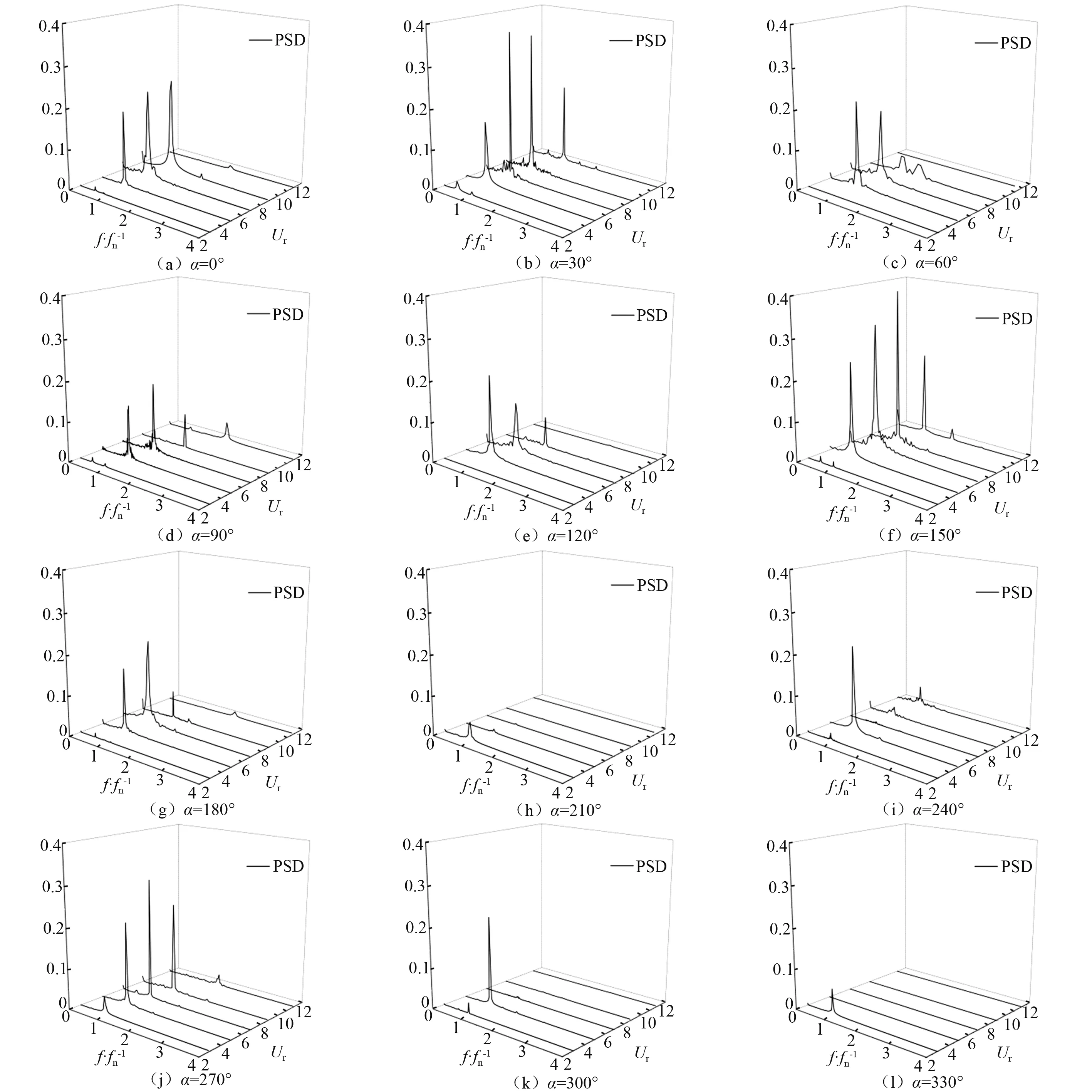
由图4(a)可看出:本文的模型和计算方法能够得到单圆柱涡激振动中的不同分支(初始支、上支和下支),能够模拟初始支和上支之间的突变现象;本文结果比Khalak等研究的结果偏小;Guilmineau等和Pan等研究的数值模型未能在Ur=5附近捕捉到大位移振幅,当前数值模型的模拟结果优于这些模型的结果。由图4(b)中可看出,本文的涡激振动频率与Khala等研究的结果和Guilmineau等及Pan等研究的结果在4 为进一步验证模型和计算方法对多圆柱系统的适用性,本文对Huera-huarte等的试验模型进行了数值模拟。单一控制杆位于主圆柱的下游,且与主圆柱刚性连接(两圆柱同步运动)。主圆柱直径为D,控制杆直径为d,且圆柱之间的间距比为G/D=1.3。本文固定圆柱直径比为d/D=0.2,固定来流速度为U∞。主圆柱直径为D=0.05 m,基于主圆柱直径的雷诺数为Re=13 000。圆柱系统的质量比为m*=2.57,阻尼比为ζ=0.003 5。采用k-ω湍流模型,入口边界上的初始湍流强度为3%。通过改变系统的刚度系数ks改变系统的固有频率,进而模拟不同约化速度下的涡激振动。采用的计算区域为55D×30D,主圆柱的中心位于原单圆柱中心位置。采用非结构网格对计算域进行离散,第一层网格厚度满足y+≈1。 表2和表3为本文计算结果与试验结果的比较。由表2和表3可知,本文结果与Huera-huarte等研究的结果契合度较高,即本文中的数值模型和计算方法能够可靠地模拟高雷诺数下双圆柱系统的涡激振动。 表2 串列圆柱系统无量纲涡激振动幅值 表3 串列圆柱系统无量纲涡激振动频率 2.3 实尺寸钻井隔水管系统的涡激振动数值模拟结果 为揭示实尺寸钻井隔水管系统在海洋环境中的涡激振动特性,本文对正在南海服役中的某实尺寸钻井隔水管系统进行模型简化。由于实尺寸钻井隔水管系统结构复杂、所处环境变化大、计算量大、耗时长,因此,只对其在不同来流攻角(0°,30°,60°,90°,…,330°)下的典型约化速度(Ur=3,5,7,9,12,即典型雷诺数相当于21 000,35 000,49 000,63 000,83 000)时的涡激振动进行二维数值模拟研究,讨论来流攻角和约化速度对其振幅、振动频率和在水平面上的运动轨迹的影响。 2.3.1 涡激振动幅值 图5为实尺寸钻井隔水管系统在不同来流攻角下,横流向无量纲涡激振动幅值随约化速度的变化。以下所讨论的涡激振动强弱均指隔水管涡激振动幅值的大小。为分析比较,图中实线为与主管直径相同的单圆柱的横流向涡激振动幅值。由图5可知,由于附属管分布的多管、多尺寸和不规则排布等特性,实尺寸钻井隔水管系统的涡激振动幅值变化规律差异明显。在约化速度3 图5 实尺寸钻井隔水管系统涡激振动幅值随约化速度的变化Fig.5 The VIV amplitude of the drilling riser system with reduced velocity 当来流攻角为0°和30°时,隔水管系统涡激振动幅值先随约化速度的增大而增大到Ur=9,然后在9 图6为实尺寸钻井隔水管系统在不同约化速度下,横流向无量纲涡激振动幅值随来流攻角的变化。由图6可知,在约化速度Ur=3时,钻井隔水管系统在任意来流攻角下的涡激振动幅值都很小,来流攻角为330°时最大约为0.1D。随约化速度增大,涡激振动幅值整体也随之增大,在约化速度为Ur=7、来流攻角为150°时达到最大,但仍小于单圆柱的振幅。随约化速度继续增大,涡激振动幅值又整体减小。当来流攻角为210°和330°时,任意约化速度下涡激振动幅值均很小,说明在此来流攻角下附属管对钻井隔水管的涡激振动抑制效果最好。 图6 实尺寸钻井隔水管系统涡激振动幅值随来流攻角的变化Fig.6 The VIV amplitude of the drilling riser system with angle of attack 2.3.2 涡激振动频率 图7为实尺寸钻井隔水管系统在不同来流攻角下的横流向涡激振动位移功率谱。由图7中可看出:当来流攻角为0°,120°,180°和270°、约化速度为5,7和9时,功率谱有峰值较大的唯一主频,且主频大小接近于隔水管系统的固有频率,表明此时振动较为剧烈,相应的涡激振动幅值较大;当来流攻角为30°,90°和150°、约化速度为5,7,9和12时,隔水管系统有峰值较大的唯一主频,且主频大小接近于隔水管系统的固有频率,表明此时涡激振动较剧烈;当来流攻角为60°、约化速度为5和7时,功率谱有峰值较大的唯一主频,且主频大小接近于隔水管系统的固有频率,表明此时振动较为剧烈振动幅值较大,而在约化速度为9时功率谱有2个较为明显的峰值,表明此时为多频振动;当来流攻角为210°和330°、功率谱只在约化速度为3时,有一个峰值较小的主频,其余约化速度下未见明显主频,表明此时涡激振动整体较为微弱;当来流攻角为240°、功率谱在约化速度为5和12时,各有一个峰值较大的主频,且主频大小接近于隔水管系统的固有频率,表明此时涡激振动较为剧烈,相应的振动幅值较大;当来流攻角为300°、功率谱只在约化速度为5时,有一个峰值较大的主频,且主频大小接近于隔水管系统的固有频率,表明此时涡激振动较剧烈。 图7 实尺寸钻井隔水管系统在不同来流攻角下的涡激振动频谱Fig.7 The VIV frequency power spectrum of the drilling riser system at different angle of attack 2.3.3 涡激振动轨迹 图8为实尺寸钻井隔水管系统涡激振动稳定后在水平面上的运动轨迹。由图8可知,在任意来流攻角下随约化速度的增大运动轨迹整体向右移动。这表明随着来流速度的增大隔水管系统的顺流向平均位置逐渐右移。由于附属管的多尺寸和非均匀布置,隔水管系统涡激振动稳定后的运动情况也较复杂,相应的运动轨迹也复杂多变,呈现出扁平椭圆形、椭圆形、倒立雨滴形、雨滴形、倾斜“8”字形及杂乱不规则等形状。 当来流攻角为0°时,可以观察到四种不同类型的运动轨迹:约化速度为3和12时杂乱无章;约化速度为5时呈近似椭圆形;约化速度为7时呈倾斜的倒立雨滴形;约化速度为9时呈略微倾斜的非对称“8”字形。当来流攻角为30°时,可以观察到两种运动轨迹:约化速度为3,7和9时杂乱无章;约化速度为5和12时呈倾斜的倒立雨滴形。当来流攻角为60°时,可以观察到三种不同类型的运动轨迹:约化速度为3和12时杂乱无章;约化速度为5和7时呈近似于一条斜线的扁平椭圆形;约化速度为9时呈扁平倾斜的倒立雨滴形。当来流攻角为90°时,运动轨迹在所有约化速度下都杂乱无章。当来流攻角为120°约化速度为5时,运动轨迹呈倾斜椭圆形,其他约化速度下杂乱无章。当来流攻角为150°时,可以观察到:约化速度为3,5,7和9时运动轨迹杂乱无章;约化速度为12时呈扁平的倾斜雨滴形。当来流攻角为180°、约化速度为5,7和9时,运动轨迹呈倾斜的雨滴形,且约化速度为9时的运动轨迹处于约化速度为7时的包络线内。当来流攻角为210°和330°时,涡激振动在所有约化速度下都很微弱,运动轨迹杂乱。当来流攻角为240°约化速度为5时,运动轨迹呈倾斜的扁平椭圆形,其他约化速度下杂乱无章。当来流攻角为270°时,可以观察到三种不同的运动轨迹:约化速度为3和12时杂乱无章;约化速度为5时呈椭圆形;约化速度为7和9时呈雨滴形。当来流攻角为300°、约化速度为5时,运动轨迹呈倾斜的扁平椭圆形,其他约化速度下杂乱无章。 图8 实尺寸钻井隔水管系统在不同来流攻角下的涡激振动轨迹Fig.8 The VIV trajectory of the drilling riser system at different angle of attack 本文基于RANS方程,采用k-ω湍流模型,用嵌入多圆柱运动求解模块的OpenFOAM求解器,对不可压缩流体进行求解,再耦合结构动力学模型进行流固耦合求解。研究了亚临界区雷诺数为20 000~85 000、典型约化速度为3~12、来流攻角为0°~330°的实尺寸钻井隔水管系统的涡激振动问题。对不同来流攻角和约化速度下实尺寸钻井隔水管系统的涡激振动幅值、频率和运动轨迹进行了分析研究。结果表明: (1) 附属管对钻井隔水管的涡激振动总体上具有抑制作用,抑制效果与来流攻角和约化速度密切相关。当来流攻角为210°和330°时,隔水管系统在所有约化速度下的涡激振动都很微弱,此时的抑制效果最好。 (2) 钻井隔水管系统的横流向涡激振动较剧烈时功率谱有峰值较大的唯一主频。此时主频大小接近于隔水管系统的固有频率。 (3) 钻井隔水管系统的涡激振动运动轨迹有多种形状,如扁平椭圆形、椭圆形、倒立雨滴形、雨滴形、倾斜“8”字形及杂乱不规则等。2.2 双圆柱涡激振动数值模拟结果

3 结 论

