基于动态黏结滑移性能的钢筋混凝土分离式模型研究
刘 智,赵兰浩,吴晓彬,周永门,王 姣
(1. 江西省水利科学研究院,南昌 330029; 2. 河海大学 水利水电学院,南京 210098)
在地震荷载作用下,高混凝土坝将不可避免地在坝体断面突变处及材料分区界面等部位出现易损区域,配筋已成为必不可少的工作,因此正确反映钢筋与混凝土之间的相互作用是仿真分析的重要方向。常规的钢筋混凝土有限元分析通常采用分布式模型、嵌入式模型或分离式模型。其中:分布式模型假定钢筋均匀分布于混凝土实体单元内,通过实体单元积分点叠加钢筋刚度贡献的形式模拟钢筋混凝土相互作用;嵌入式模型则采用杆单元或梁单元模拟钢筋,通过位移约束条件强制钢筋单元与混凝土单元位移协同,最终将钢筋的刚度贡献等效叠加到混凝土节点处;分离式模型将分别离散钢筋单元与混凝土单元,在两者单元节点之间设置弹簧单元或接触单元,结合联结单元的黏结-滑移本构关系模拟钢筋混凝土之间的相互作用。
分布式模型和嵌入式模型假设钢筋混凝土不产生相对滑移,主观消除了钢筋位移自由度的运算,同时有限元模型中网格离散相对简单,因此计算效率较高。目前学者多采用此类模型进行水工结构抗震的仿真计算:龙渝川等[1-2]基于分离式模型的理念,在钢筋单元与混凝土单元交界面部位嵌入无厚度单元,通过约束条件使黏结单元上、下表面与混凝土单元和钢筋单元位移协同,以黏结单元上、下表面的位移差表征钢筋与混凝土的相对滑移量,结合虚功原理建立了一种嵌入式滑移模型,并基于该模型研究了混凝土重力坝抗震配筋的加固效果,研究表明,配置坝面钢筋对限制混凝土形成集中裂缝的效果明显,同时考虑钢筋滑移时将对裂缝分布造成的影响;沈怀至等[3]采用嵌入式模型将钢筋与混凝土材料的断裂能加权平均作为钢筋混凝土的断裂能,通过塑性损伤模型对Koyna坝不同配筋方案的抗震性能展开研究,对比了配筋措施对损伤分布范围与坝顶动力响应的影响;艾亿谋等[4]分别运用分布式模型和分离式模型对Koyna坝进行配筋后的抗震分析,并提出分布式模型中钢筋混凝土等效强度和等效模量的简化公式;张社荣等[5]认为目前常用的分离裂缝模型和弥散裂缝模型对网格的依赖性高,给数值仿真带来了极大的前处理工作量,因此采用基于单位分解的扩展有限元(extended finite element method, XFEM),使得节点影响域上对非连续位移场的表征独立于单元边界,结合嵌入式模型,探讨了强震区混凝土重力坝配筋对其抗震性能的影响;李静等[6]采用嵌入式模型与塑性-损伤耦合模型,对Koyna坝未配筋与两种不同配筋形式的地震响应进行仿真,验证了Koyna坝在坝头薄弱部位布置抗震钢筋的必要性和实用性。
对于地震荷载而言,循环往复的荷载特性使得钢筋对混凝土的刚度贡献并不是一成不变的,分布式模型和嵌入式模型无法精准描述两者之间黏结滑移性能的变化过程,从而无法反映黏结性能变化对整体结构或局部构件承载能力和裂缝发展的影响。本文基于单弹簧联结单元法建立钢筋-混凝土分离式模型,并搭建合理的钢筋混凝土动态黏结-滑移本构关系,结合混凝土四参数损伤模型,建立高效的钢筋与混凝土相互作用模拟方法,旨在为实际混凝土工程配筋后的抗震复核验算提供进一步的保障。
1 基于单弹簧联结单元法的分离式模型
传统的双弹簧联结单元法需要人为选择法向刚度,避免单元发生法向嵌入,较大的取值往往影响迭代过程导致计算不收敛。因此,在此基础上建立一种基于混合坐标系的单弹簧联结单元法,通过法向约束强制混凝土单元与钢筋单元间的法向自由度协同,通过设置切向弹簧模拟两者之间的切向作用,切向刚度则通过黏结-滑移本构关系确定[7]。如图1所示,单弹簧联结单元法采用实体单元模拟混凝土,使用杆单元或梁单元模拟钢筋,在混凝土与钢筋接触部位设置重复节点分别作为混凝土与钢筋插值点,并建立弹簧单元作为两者间的联结单元。该方法在整体坐标系内求解实体单元,其法向自由度关系表达简单明确;在局部坐标系内求解杆单元或梁单元,建立法向自由度约束方程保证法向变形协同,避开双弹簧单元法等人为选择法向刚度的困难,求解效率将得到显著提高,方法正确性与适用性已经过可靠的验证[8]。
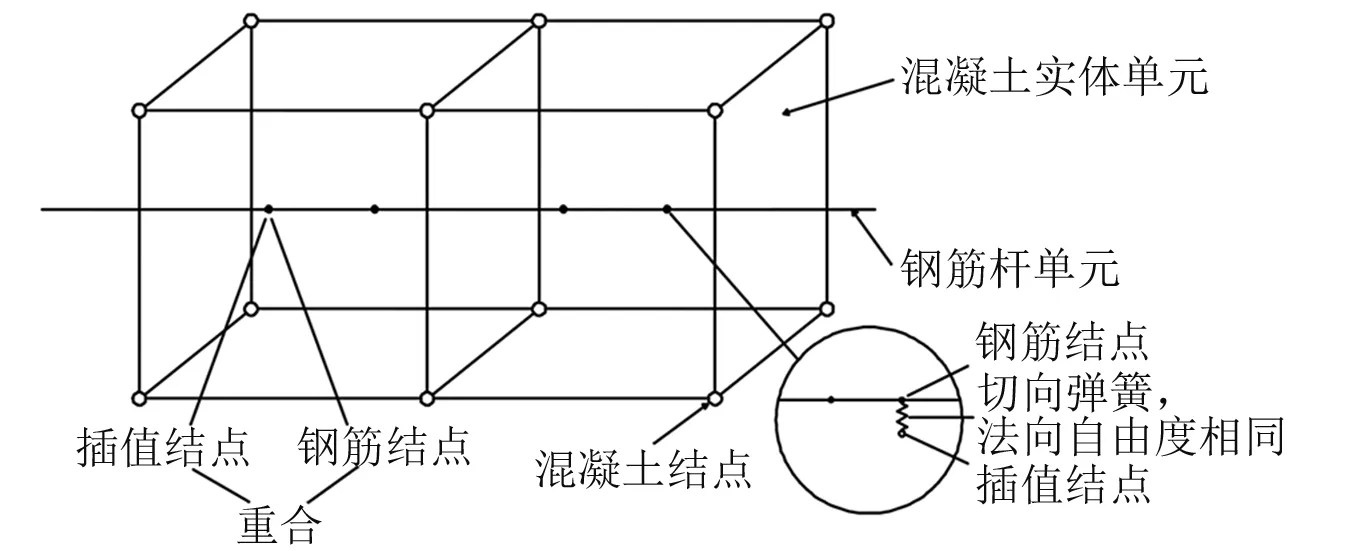
图1 单弹簧联结单元法求解示意图Fig.1 Diagram of single-spring joint element method
1.1 坐标转换方式
采用单弹簧联结单元法求解钢筋混凝土问题时,钢筋杆单元或梁单元的刚度矩阵通常在局部坐标系中求解,为建立完整的平衡方程,需要将局部坐标系中杆单元的自由度转换到整体坐标系。混合坐标系求解方法能够使有限元方程的求解不依赖于坐标系的选择,不同部分可以选择不同的参考坐标系。如图2所示:Oxyz为混合坐标系中的整体坐标系;O′x′y′z′为钢筋单元局部坐标系;O*x*y*z*为钢筋单元节点局部坐标系,用于协调相邻钢筋排列方向,通过节点相邻钢筋单元联合推求平均值。

图2 混合坐标系示意图Fig.2 Schematic diagram of mixed coordinate system
建立各坐标系间转换矩阵,假定:R为坐标系Oxyz与O′x′y′z′的坐标转换矩阵;r为坐标系Oxyz与O*x*y*z*的坐标转换矩阵。各坐标系关系为
(1)
式中,u,F,u′,F′,u*,F*分别为Oxyz,O′x′y′z′,O*x*y*z*中的位移向量和荷载向量。
通常对于三维空间问题,坐标转换矩阵R还可以看作是绕Z轴旋转建立的,因此可以写成
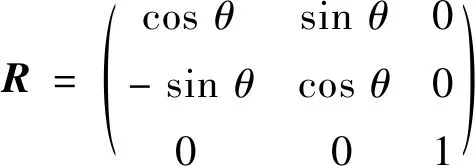
(2)
式中,θ为绕Z轴的旋转角。
局部坐标系下梁单元与节点单元的有限元平衡方程为
(3)
式中:k*=rkrT=rRk′RrT;k,k′,k*分别为Oxyz,O′x′y′z′,O*x*y*z*中的刚度矩阵。
1.2 法向约束方程
单弹簧联结单元法通过在钢筋单元与混凝土单元交接处设置重复节点,根据重复节点信息建立两者法向关系。不同于传统双弹簧联结单元法,单弹簧法采用不协调网格中位移协调解法取代法向弹簧,令重复节点法向自由度相同以达到法向固定的目的,避免了大数值法向弹簧刚度导致的数值计算迭代不收敛。
钢筋单元法向位移插值由式(4)推求
(4)
式中:n为模型维数;rij为插值系数。
钢筋网格的划分具有随机性且相对实体单元过于密集,因此混凝土单元与钢筋单元通常不协调,即节点位置不重合。单弹簧联结单元法通过对双节点中钢筋单元周围的混凝土单元节点位移进行插值,确定相应钢筋节点的法向位移,以此进行法向约束
(5)
(6)
式中:m为被插值节点周边节点个数;a为节点插值系数,即形状函数。
1.3 钢筋与混凝土之间的相互作用
以增量的形式建立有限元平衡方程模拟钢筋与混凝土之间的相互作用
(7)
式中:f*为局部坐标系O*x*y*z*中混凝土作用于钢筋的力,根据作用力的相互关系; -rTΔf*为整体坐标系Oxyz中钢筋作用于混凝土的力。
单弹簧联结单元法在重复双节点处强迫法向自由度相等,因此混凝土与钢筋之间法向位移及作用力无需计入平衡方程。式(8)中f*仅为重复双节点处的切向作用力,其表达式为
(8)
式中:f为黏结强度;s为黏结强度对应滑移量;D为钢筋直径;l为钢筋长度;ds为当前滑移量。
将式(8)代入式(7)并改写为矩阵形式,即单弹簧联结单元法有限元平衡方程
(9)
2 动态黏结滑移本构关系
2.1 黏结-滑移本构关系骨架线的选择
在单调轴向加载作用下,钢筋混凝土黏结-滑移本构关系骨架线与其相互作用机理关系密切,可分为胶结阶段、强度上升阶段、强度峰值阶段、强度退化阶段和摩擦稳定阶段。依据该理论建立的徐有邻五段线模型被我国GB 50010—2010《混凝土结构设计规范》[9]所采用,本文模型中骨架线选用规范模型。
2.2 循环荷载下黏结-滑移本构关系建立
循环荷载下钢筋混凝土动态黏结-滑移本构关系的建立依托于动态试验中观测的加、卸载路径,即重新加载曲线、卸载曲线及反向加、卸载曲线。本文将循环荷载下钢筋混凝土黏结-滑移滞回关系简化为多线段形式进行表达,如图3所示,其中卸载特征参数选用滕智明等[10]的试验拟合参数:

图3 动态黏结-滑移本构关系示意图Fig.3 Diagram of dynamic bond slip constitutive relationship
(1) 加载阶段——如图4(a)所示,在黏结-滑移关系到达稳定阶段之前,钢筋横肋间混凝土尚未完全破坏,卸载时钢筋横肋与混凝土之间将存在不同程度的残余滑移量(B点),量值大小与卸载滑移量相关但不相等,其间差异由材料弹性与塑性变形特性决定。
(2) 卸载阶段——如图4(b)所示,卸载时黏结强度迅速下降至应力零点,由于黏结-滑移关系间钢筋与混凝土的弹性与塑性变形占比微小,因此卸载刚度很大,根据滕智明等的试验经验参数取295 N/mm3。此后黏结强度将降至卸载摩擦段(C-D),并保持该强度直至滑移零点。卸载摩擦段的黏结强度按试验的经验公式确定,τup=-afτun,其中黏结摩擦因数af取0.12。

图4 动态黏结-滑移本构关系加、卸载示意图Fig.4 Loading and unloading diagram of dynamic bond slip constitutive relationship
(3) 反向加、卸载阶段——钢筋混凝土黏结-滑移性能在机理上与施载方向无关,但外荷载的施加则有方向的区分,其循环荷载下的滞回关系按原点中心对称。如图5所示,当卸载至滑移零点后开始反向加载,此时钢筋横肋另一侧混凝土并未发生破坏,且前一阶段产生的劈裂裂缝将受到挤压闭合继续承载,反向加载阶段的机械咬合力和摩擦力同初始加载状态数值大致相同,但方向相反。因此反向加载下的黏结-滑移关系将沿中心对称骨架线行进,反向卸载机理与前述同样相似。

图5 动态黏结-滑移本构关系反向加载示意图Fig.5 Reverse loading diagram of dynamic bond slip constitutive relationship
(4) 上述黏结-滑移关系机理仅适用于首次循环。如图6所示,当循环次数增加,前期荷载作用下钢筋混凝土之间已丧失的化学胶着力与机械咬合力是无法恢复的,其峰值黏结强度将显著降低,并且加载过程将不再经历胶结阶段与上升阶段。峰值黏结强度G点的退化速度将随循环次数的增加而减缓,同时与应力水平的变幅相关,当应力水平由低到高时影响较小,反之应力水平由高到低时影响显著。
(5) 当黏结-滑移关系处于稳定阶段后,钢筋肋间混凝土完全破坏,钢筋与混凝土之间的黏结强度值均由摩擦力提供并保持恒定,其数值与滑移量及施载方式无关。
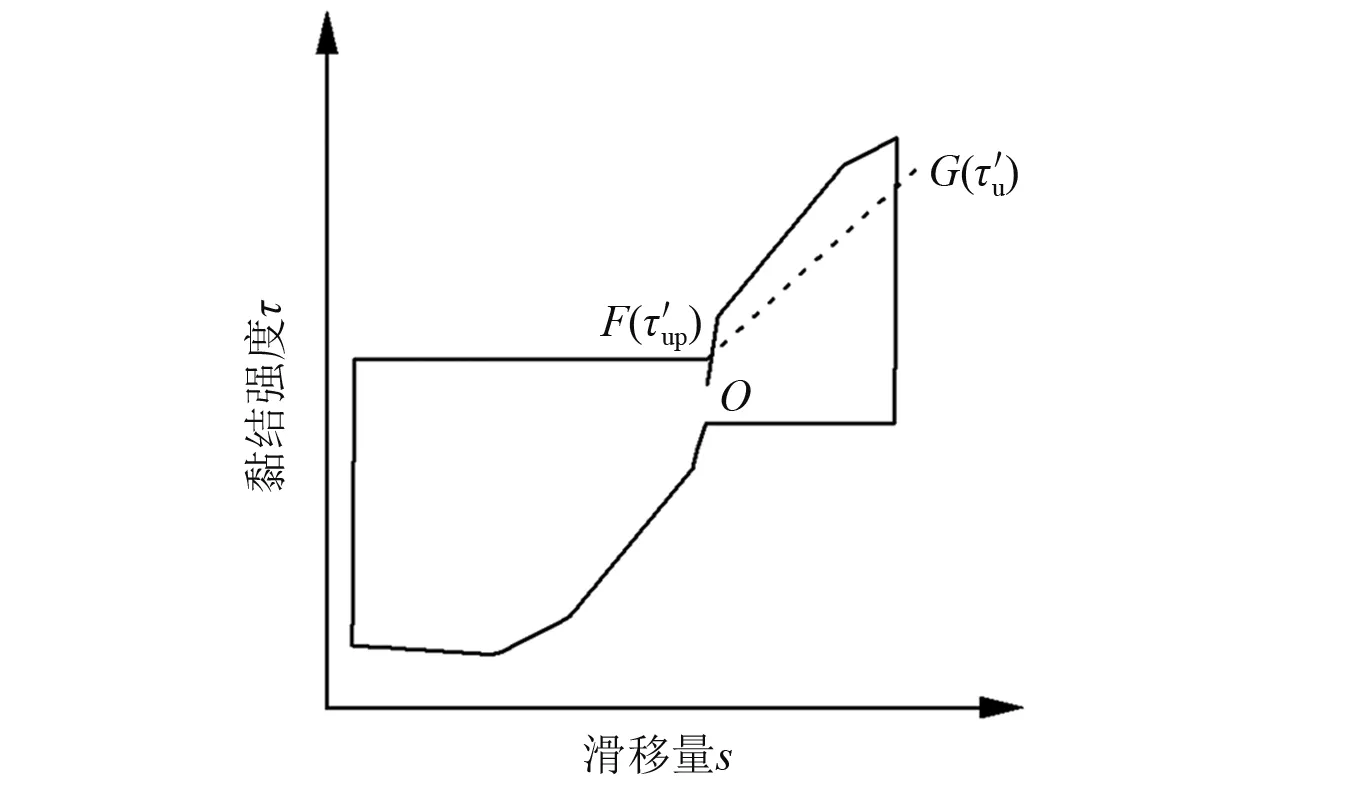
图6 动态黏结-滑移本构关系强度退化示意图Fig.6 Strength degradation diagram of dynamic bond slip constitutive relationship
3 混凝土损伤模型
基于Hsieh-Ting-Chen的应力空间四参数破坏准则,韦未等[11]建立了一种基于应变空间的四参数破坏准则

(10)

韦未等[12]基于四参数破坏准则的基本思路,提出了一种新的四参数等效应变计算方法。假定四参数破坏准则在应变软化段内仍然适用,且A,B,C,D四个参数保持不变,其形式与式(10)相同,式中ε0被等效应变ε*替代
(11)

ε*=
(12)
该式形式简单明了,同时可将复杂的多轴问题转化为简单的单轴问题。损伤变量则采用Faouzi公式计算
(13)
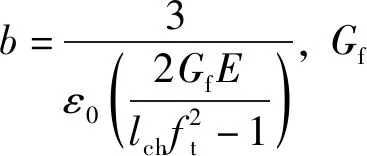
该模型的合理性和正确性在已有的研究中已经得到了充分的验证[13-14]。
4 算例验证
通过Fortran语言编译模型相应计算模块,并嵌入现有大型有限元仿真软件,选取经典算例对模型进行数值验证。
4.1 四点弯曲梁数值验证
选取Walraven[15]四点弯曲梁试验作为研究对象进行准静态算例验证。梁构件试验模型如图7所示,模型尺寸为4.1 m×0.2 m×0.45 m,梁内不设置腹筋,在底部40 cm处布置三根不同直径钢筋,模型左侧支点施加双向约束,右侧支点施加法向约束,顶部进行对称的位移分级加载。模型混凝土材料参数如表1所示。

表1 算例材料参数
图8给出了本文模型在不同荷载下的计算结果。混凝土首先在中部拉应力集中区域形成垂直裂缝,随后在模型承载不断提升的过程中,混凝土出现了由剪应力导致的约束支座点至顶部加载点的斜向45°剪切裂缝,最终剪切裂缝形成贯穿破坏。对比Zhao等给出的数值模拟结果,网格的细化剖分使得破坏路径更为明确,结果数值也更为接近试验数据。
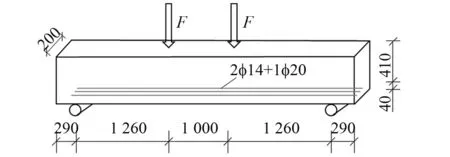
图7 四点弯曲梁试验模型示意图Fig.7 Diagram of four point bending beam model

图8 不同承载下梁模型损伤破坏模式Fig.8 Damage and failure modes of beam model under different loads
图9对比了本文的仿真结果、Zhao等的仿真结果以及Walraven试验模拟结果对应的荷载-挠度曲线。曲线被分为两个阶段:前一阶段混凝土材料本质上处于弹性变形,钢筋与混凝土材料之间的相对应变十分微小,荷载-挠度关系近乎线性;后一阶段混凝土将在持续的增荷状态下发生破坏,开裂致使截面的刚度降低,当裂缝发展至钢筋部位后拉应力将完全由钢筋承担,挠度的增长速率将大幅提升。
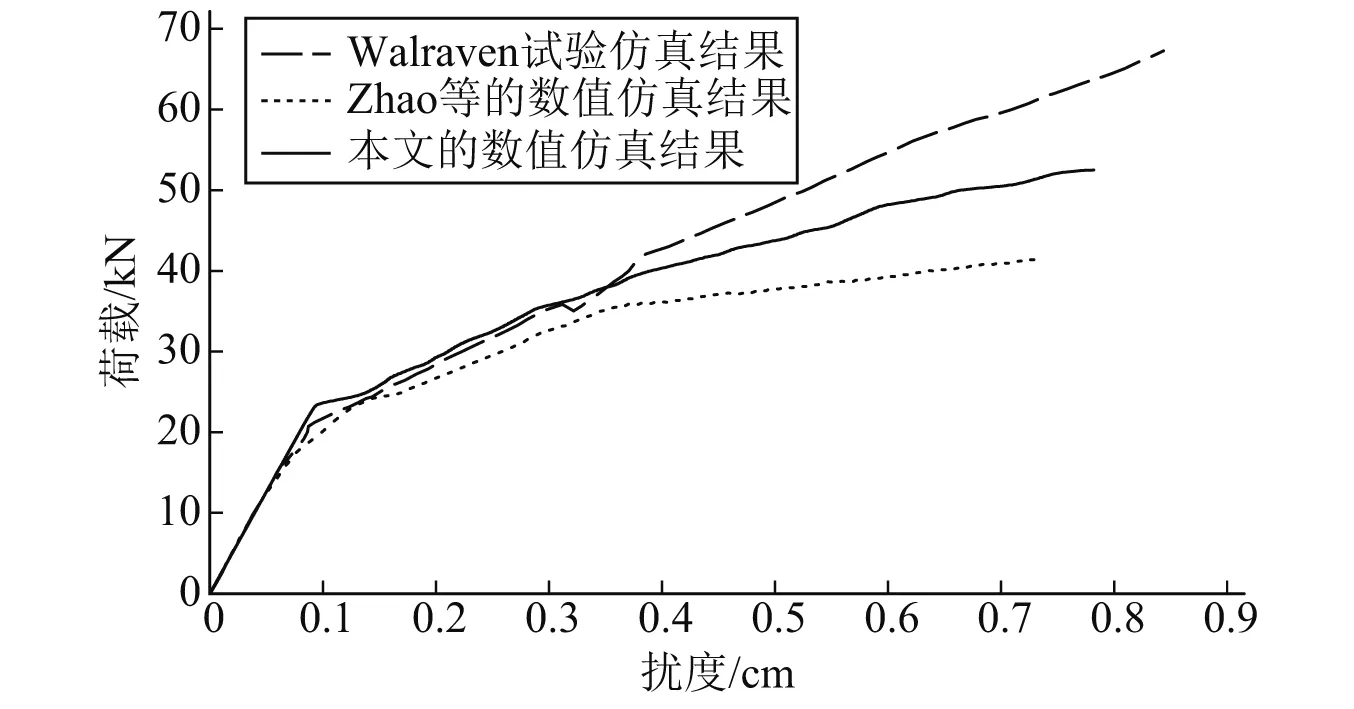
图9 四点弯曲梁荷载-挠度曲线对比示意图Fig.9 Diagram of load deflection curve comparison of four point bending beam
图9表明:Walraven试验中失效破坏时的承载约为70 kN;Zhao等的数值模拟结果约为40 kN;而本文最终失效破坏时的承载约为55 kN。通过分析,初步判断与试验数据的差异原因在于数值模拟的基本假定无法考虑真实试件中部分剪切应力的传递机制。
4.2 单轴循环荷载作用数值验证
选取Shima等[16]的10号拉伸构件作为研究对象,圆柱体构件的三维有限元模型如图10所示,直径为0.5 m,长度为0.76 m,模型中心处设置一根直径为19 mm的钢筋,在模型圆截面平行于坐标轴Y和坐标轴Z的外表面设置切向约束,钢筋两侧施加反方向的位移分级加载。

图10 钢筋混凝土梁有限元示意图Fig.10 Finite element diagram of reinforced concrete beam
选取试件侧表面位置钢筋节点作为特征点以验证本文模型的正确性。图11给出了特征点在循环荷载下的黏结滑移关系变化过程,可见所编译计算模块的仿真结果能够准确反映所嵌入的本构模型。

图11 循环荷载下侧表面钢筋节点黏结滑移关系示意图Fig.11 Diagram of bond slip relationship of reinforced node on side surface node under cyclic load
图12与图13分别给出了特征点处于黏结强度峰值时钢筋变形与滑移量沿长度方向的分布情况。当端部荷载为拉加载时,钢筋各部位相对中点的轴向变形受黏结效应影响逐步降低,如图14所示,循环荷载下构件中点附近钢筋与混凝土之间的黏结性能仅丧失了化学胶着力,机械咬合力仍发挥着决定作用,黏结强度处于上升阶段。黏结效应的影响同样在滑移量的分布规律上得到体现,但由于数值计算结果按照方向区分正负,为与试验结果对比,对钢筋变形数值作绝对值处理。黏结峰值时钢筋变形分布与Shima试验中一级加载与二级加载时钢筋变形分布形成了良好的过渡。当端部荷载开始卸载并转至压加载黏结峰值时,钢筋变形分布与拉加载时有所差异。此时钢筋端部变形较大,端部向中点方向分布受混凝土保护层约束并结合钢筋混凝土自身的黏结效应,钢筋变形急剧下降至平稳阶段,滑移量分布图表现出同样的规律,端点特征值达到受压黏结峰值时多数部位仍处于强度上升阶段或是胶结阶段。本算例模拟结果与钢筋混凝土黏结滑移机理表现相同,结合Shima试验数据,客观验证了本文模型的正确性。

图12 特征点受拉黏结峰值时钢筋变形与滑移量沿长度分布示意图Fig.12 Distribution diagram of reinforcement deformation and slip along the length at the peak value of tensile at the characteristic point
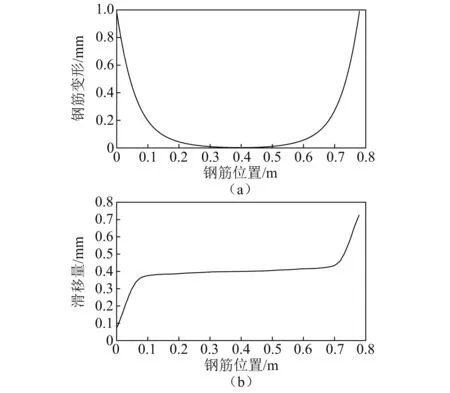
图13 特征点受压黏结峰值时钢筋变形与滑移量沿长度分布示意图Fig.13 Distribution diagram of reinforcement deformation and slip along the length at the peak value of compression at the characteristic point
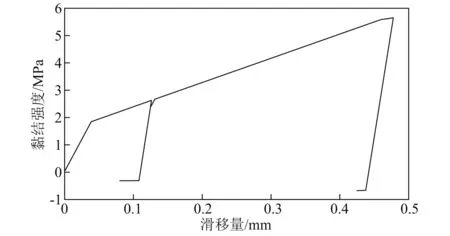
图14 循环荷载下钢筋0.5 m处节点黏结滑移关系示意图Fig.14 Diagram of bond slip relationship of joints at 0.5 m of reinforcement under cyclic load
4.3 Koyna重力坝震况验证
选取Koyna重力坝作为研究对象进行工程验证,分别对坝体素混凝土以及两种不同配筋方案进行仿真计算,分析地震荷载作用下坝体表层配筋对大坝整体动力响应及最终破坏模式的影响。本算例以模型可靠性为研究目标,因此未对配筋量及钢筋布置形式做详细分析。如图15所示,对坝体表层进行简单配筋,上游面与下游面各布置两排直径32 mm的钢筋,保护层厚度为200 mm,钢筋间距为300 mm。配筋模式分为方案A与方案B,其中:方案A中钢筋横河向间距为500 mm;方案B中钢筋横河向间距为150 mm。
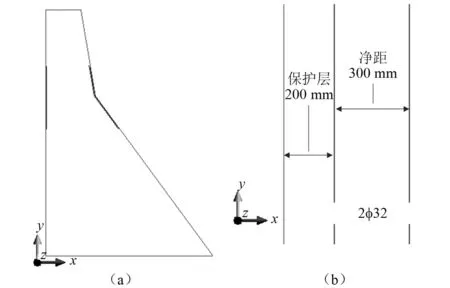
图15 Koyna重力坝模型配筋示意图Fig.15 Model reinforcement diagram of Koyna dam
Koyna重力坝尺寸参数和混凝土材料计算参数均参照文献[17],钢筋材料计算参数采用抗震钢筋HRB400E的力学性能特征值,即屈服强度σs=400 MPa,弹性模量E=200 GPa,抗拉强度ft=540 MPa。地震荷载选取Koyna地震波,其归一化的加速度时程曲线,如图16所示,地震波时长12.8 s,水平向峰值加速度为0.474g,竖直向峰值加速度为0.312g。采用Westgaard附加质量法考虑地震荷载下库水作用于坝体的动水压力。为满足对比性分析的需求,模型在实际震害发生的坝坡折角区域进行了局部精细化剖分。
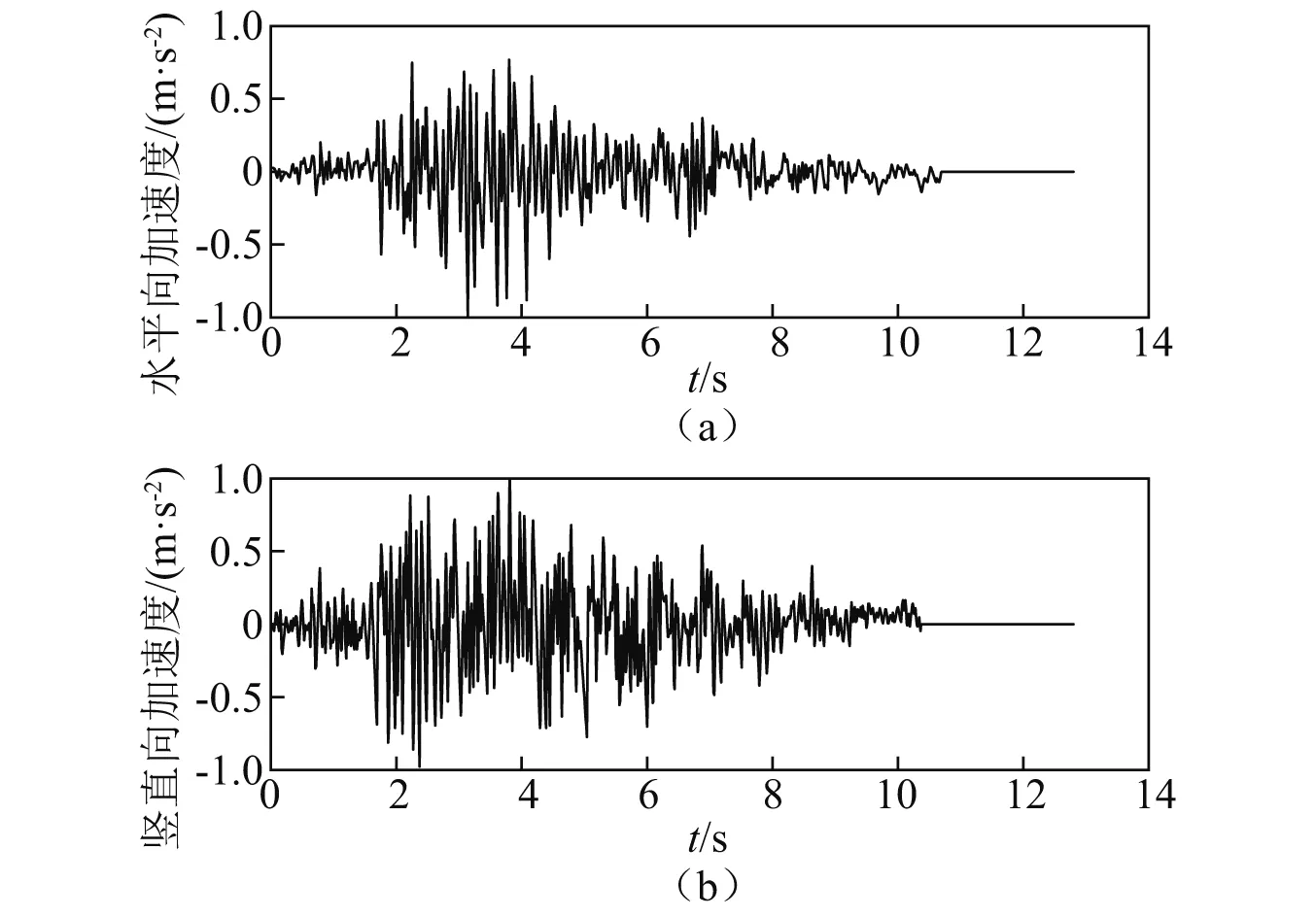
图16 Koyna地震波加速度时程曲线Fig.16 Acceleration time histories of Koyna seismic wav
图17给出了地震荷载作用下重力坝材料为素混凝土与坝体局部配筋后的损伤分布情况。当坝体表层易损区域布置抗震钢筋后,在钢筋与混凝土的协同作用下,坝体损伤破坏程度降低,但表层的损伤演化区域明显扩大,并且损伤破坏程度与损伤演化面积将随配筋量的增加而显著降低。这说明局部配筋能够起到一定程度的限裂作用,提高坝体的抗震性能,此仿真结果能够反映工程界的普遍认知。
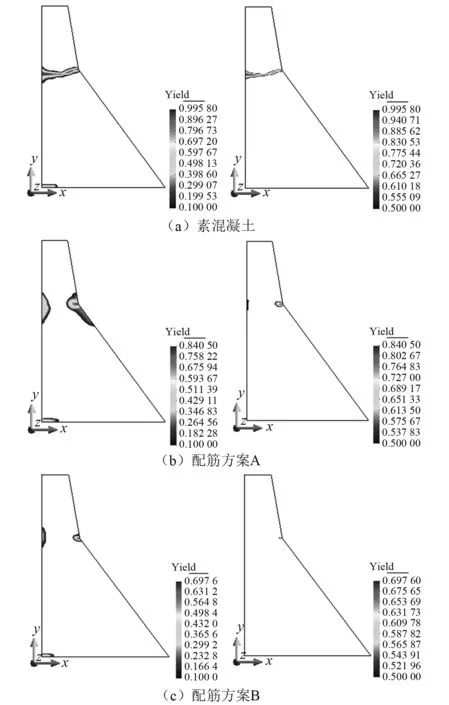
图17 Koyna重力坝地震荷载下损伤分布图Fig.17 Damage distribution of Koyna dam under seismic load
选取上游面坝顶部位作为动力响应分析特征点,对比Koyna大坝素混凝土与两种配筋方案下的位移响应趋势。地震荷载下特征点的位移时程图,如图18所示,分析结果显示坝体的损伤演化均发生在5 s之前,同时受限于有限元计算方法的小变形基本假定,当大坝的坝头部位发生损伤贯通后其相应的数值模拟结果并不具有参考性,因此对特征点进行变形特性分析时选取0~5 s的时间段。
重力坝表层配筋后坝体整体刚度提升,在相同地震动荷载作用下坝体整体位移降低,周期延长,该变形特性在特征点顺河向与竖直向的位移时程图中均有体现。特征点的动力响应与损伤演化结果能够相互验证:坝体下游面坝坡折角部位在2.7 s左右进入损伤,坝顶位移同期出现增幅,随着损伤持续深入,坝体整体刚度降低,震动导致的位移幅度逐渐增大,进一步影响损伤演化速度;当地震持时达到4 s左右,坝体未配筋时坝坡折角部位损伤已接近贯通,位移将出现突变,而坝体配筋后并未出现损伤贯通,混凝土材料处于软化阶段且仍存在一定的承载能力。因此位移幅度虽然同样增大但并未出现突变现象,这同样说明局部配筋能够有效提高坝体的抗震性能。
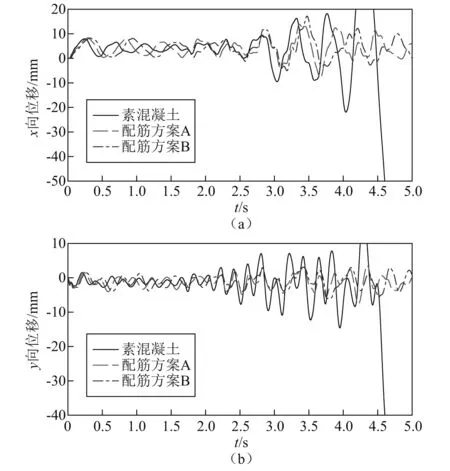
图18 地震荷载下特征点位移时程图Fig.18 Displacement time histories of characteristic point under seismic load
5 结 论
本文针对高混凝土坝局部配筋后的非线性抗震问题,建立了循环荷载作用下基于钢筋混凝土动态黏结滑移性能的分离式模型,并结合经典算例验证了模型的正确性及适用性。模型的优势在于能够准确模拟循环荷载下钢筋混凝土黏结滑移性能的变化过程,同时对比传统的双弹簧联结单元模型,能够避免人为选择法向刚度的困难,并且局部坐标系与整体坐标系混合求解的方式使方法不受钢筋布置方式与单元网格剖分的限制,迭代收敛速度快,计算过程简单便捷,能够为混凝土工程配筋后的抗震复核验算提供进一步的保障。

