计及信息畸变的低压有源配电网故障定位方法

徐凤乾，吕慧珍，巫水萍，郑志祥，乐 健

（1.国网浙江省电力有限公司衢州供电公司，衢州 324000；2.武汉大学电气与自动化学院，武汉 430072）

低压配电网是连接电网与用户、保证供电可靠性的重要环节[1-3]。长期以来，由于低压配电网的故障影响范围不大、停电损失小而未受到重视。但随着智能电网的不断发展，以及用户对供电可靠性要求的提高，低压配电网的故障定位逐渐得到研究者的关注[4-5]。

目前应用于低压有源配电网的故障定位方法主要包括基于电流相角差值及基于智能算法的判别方法。文献[6-7]提出了基于电流相角差值及零序电流的故障定位和识别方法，此方法能够适用于多种配电网结构，具有良好的自适应性与鲁棒性。文献[8]针对低压有源配电网线路参数不对称的特点，提出利用基于微扰法的相模变换方法实现含分布式电源低压配电网的区段故障定位，解决了配电网络参数不对称对定位精度的不利影响。此类方法均实现了低压有源配电网的故障定位，但其对测量设备信息提供的实时性及可靠性要求较高、容错性较差。基于智能算法的故障定位方法因原理简单且具有高容错性而成为近年来的研究热点，并已取得了良好的应用效果[9-10]。低压配电网运行环境复杂，监测信息易发生畸变，直接应用智能算法并不能完全消除信息畸变对定位准确性的影响。文献[11-12]针对保护装置与断路器误动和拒动建立了相应的目标函数，并采用改进的粒子群算法求得最优解，具有很好的鲁棒性和容错性。文献[13]提出了基于信息矛盾原理的畸变修正策略，当监测到故障时，首先通过信息矛盾原理对故障信息序列进行畸变检测，若存在矛盾信息对，则根据贝叶斯定理对局部信息进行判断，修正矛盾信息。文献[14]建立了计及FTU漏报和误报后的故障定位优化模型，采用了二进制粒子群优化-遗传算法进行模型求解，能够实现大面积通信故障情况下的故障定位。但以上方法应用于分支众多、区段数量大的低压配电网时，实用性仍存在算法设计复杂、定位准确率低的问题。

本文提出了计及信息畸变的低压有源配电网故障定位方法。在分析信息畸变类型的基础上，利用畸变因子对信息畸变进行了建模，设计了计及信息畸变的故障定位求解模型。针对低压配电网多分支的结构特点，建立了用于故障定位的模型分层方法，以提高故障定位的准确性和求解效率。通过算例验证本文所提出的故障定位方法的正确性和有效性。

1 计及信息畸变的故障定位算法

1.1 故障监测信息模型

随着低压配电网智能化、设备状态可视化技术的发展，先进状态监测技术为实现低压配电线路的实时监测提供了必要基础[15]。本文考虑的故障监测信息主要为线路过流信息，且由于低压配电线路通常较短，本文仅考虑将故障定位在某一区段内。以图1所示的简单网络为例，此网络分为3个区段，区段首端监测单元M1-M3用于监测过流信息。

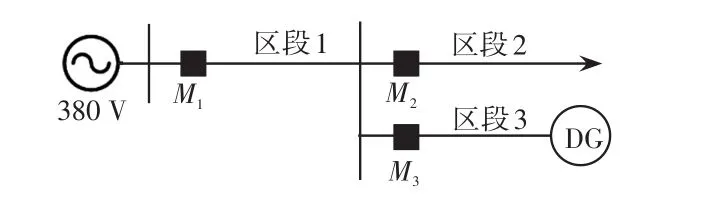
图1 多区段配电网络示意Fig.1 Schematic of distribution network with multiple zones

当某条线路发生故障时，首端监测单元可监测到故障电流，由于光伏等分布式电源的接入，使得网络功率双向流动。本文规定主电源到末端负载的方向为电流正方向，参考文献[16]的方向判据，本文采用的故障监测信息编码为

式中，Ij为第j个监测节点的监测信息，j=1、2、3。

1.2 畸变信息模型

实际运行中，负责信息采集的监测单元多位于户外，其工作环境多变，与控制中心的通信过程中会发生丢包、延迟、噪声干扰等错误，容易造成对故障区域的判定的错误。丢包会造成监测信号漏报，即故障时无过流信息告警，编码为0；延迟会造成过流信号滞后，影响故障定位的实时性；噪声干扰会造成监测信息的误报。为了准确计入监测信息的畸变情况，需对信息畸变特性进行分类。由以上分析可知，造成的信息畸变主要有以下6种情况。

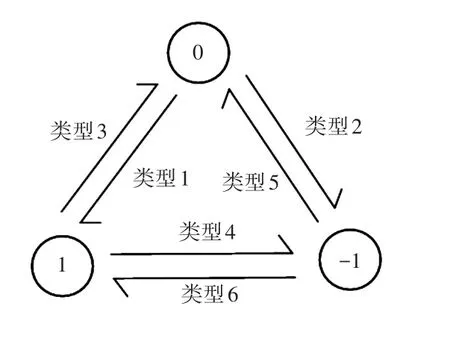
图2 信息畸变示意Fig.2 Schematic of information distortion

由图2可知，当实际电流监测信号（未发生畸变信号）为0时，其可能畸变为1或-1，即图中类型1和类型2。当实际电流监测信号为1时，其可能畸变为0或-1，即图中类型3和类型4。当实际电流监测信号为-1时，其可能畸变为0或1，即图中类型5和类型6。综合以上分析，本文提出采用畸变因子对第j个监测节点的状态监测信息的畸变情况进行建模，即监测信息的畸变类型由畸变因子确定，如表1所示。

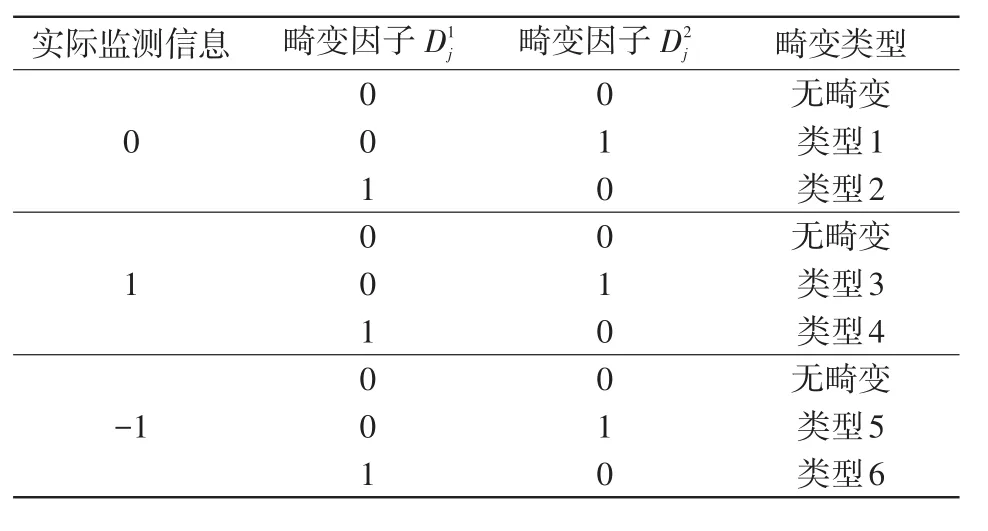
表1 畸变信息模型Tab.1 Model of distortion information

1.3 故障定位算法设计

1）决策变量

若将配电网分为N个区段，定义si为第i个区段的状态变量，si=1表示区段发生故障，si=0表示区段状态正常。考虑畸变情况，本文设计的决策变量包括N个区段的状态信息及畸变信息，具体为

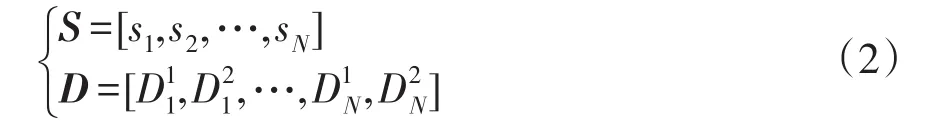
由式（2）可知，本文设计的决策变量的维度为3N。

2）目标函数

在低压有源配电网中，故障定位可以等效为求解目标函数最小值的问题。在计及信息畸变后，故障定位的目标函数可表示为

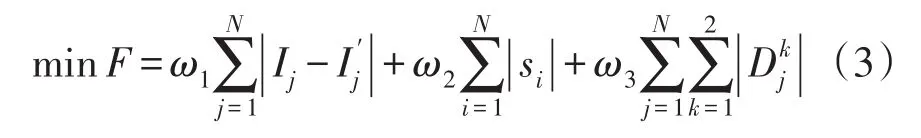
目标函数中的第一部分反映了期望监测信息与控制中心实际接收到的监测信息的逼近程度，为故障定位的主要依据。第二部分反映了故障区段的数量，即优先考虑故障区段数量少的情况。第三部分反映了信息畸变的数量，即优先考虑信息畸变数量少的情况。第二、三部分均为故障定位的辅助判据，因此有ω1≥ω2和ω1≥ω3。本文参考文献[17-18]的设计结果，设置ω1=20,ω2=0.6,ω3=1。

为了将决策变量与节点监测信息联系起来，需构建决策变量与监测信息期望值的开关函数，未计及畸变信息的开关函数如式（4）～（6）所示[16]。

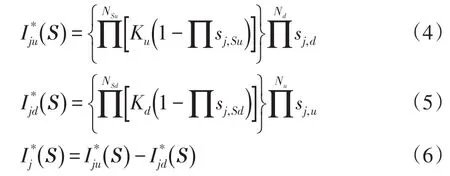
依据式（4）～（6）即可由状态信息求得无畸变时的节点监测信息期望值。同时由表1可知，计及畸变的节点监测信息期望值可由及畸变因子推导得出，其关系式如下：

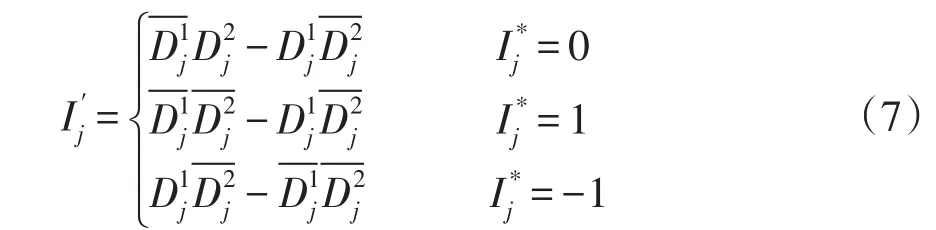
3）求解算法

由以上分析可知，本文将计及信息畸变后的故障定位问题转化为求解无约束的0-1整数规划问题。求解此问题的算法较多，但由于低压配电网多为多分支的辐射状结构，区段数目较大，导致变量维度较大，采用优化算法直接求解往往会造成定位准确率过低。若从优化算法的角度进行改进，难以从根本上避免维度较大而陷入局部收敛的问题。本文提出了将故障定位模型进行分层的方法，分层后各层模型的求解对优化算法的要求降低。

2 故障定位模型的分层求解方法

2.1 低压配电网分层等效模型

低压配电网典型的分支结构如图3所示。

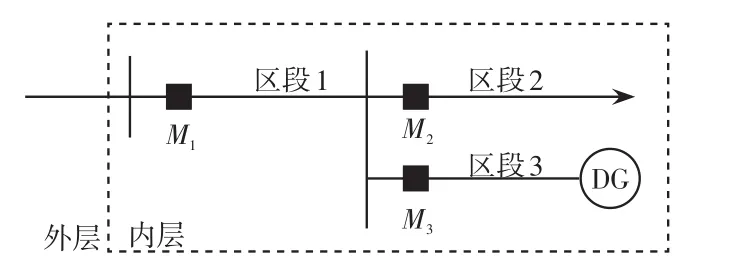
图3 配电网分支结构Fig.3 Branch structures of distribution network

根据对外等效原则，可以依据图3所示内层区域是否有DG投入，将其等效为图4所示的有源支路及无源支路的结构。

图4 分支等效模型Fig.4 Equivalent model of branches

依据图4即可建立外层整体等效模型。图4端口处监测单元M1的监测信息即为此区段的等效监测信息，其参与外层故障定位。

当外层故障定位算法判定此等效区段发生故障时，根据分界点M1的监测信息对外层进行等效，即监测信息为1时，外层等效为电源；监测信息为0或-1时，外层等效为负载，以此建立内层等效模型。通过以上等效，可确保每层故障定位的变量维度均较小，提高故障定位的准确性。

由以上分析可知，分界节点的值对故障定位的准确性影响较大，当其信息发生畸变时往往会造成故障的误报或漏报，因此分界节点应采用可靠性更高的监测设备以确保关键信息的准确性。

2.2 分层求解流程

根据区段的数量，可以将故障定位分为多层求解，图5给出了以2层为例的分层求解流程。

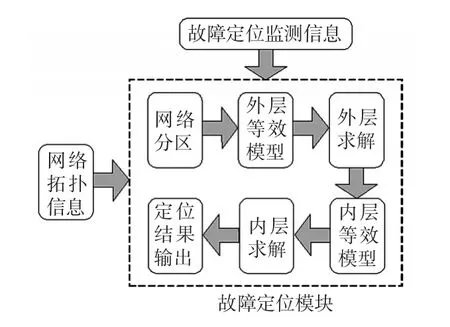
图5 分层求解流程Fig.5 Process of finding the hierarchical solution

外层求解是为了选取故障的大致区域，即分辨出故障点在外层或内层，若在内层，则识别出故障所在区域。内层求解是当外层求解选取了故障区域后，再进行精确故障定位以求解故障具体区段。

当区段数量过多时，可将内层模型继续分区并逐层求解，实现故障区段精准定位。

观察两组血糖指标，包括空腹血糖(FPG)、餐后2 h血糖(2 hPG)、糖化血红蛋白(HbAlc)。取两组治疗后空腹静脉血 3 mL，静置 2 h，3 000 r/min，离心处理 10 min，保存-80℃冰箱待检；行酶联免疫吸附法测定多聚ADP核糖聚合酶(PARP)。

本文采用二进制粒子群算法（BPSO）进行各层模型的求解，该方法具体原理可参考文献[19]。

3 算例分析

3.1 有效性验证

为了验证本文所提故障定位算法及求解方法的有效性，采用如图6所示的低压配电网算例模型。该模型共有17个监测节点、17个区段，并且有2个DG接入。

设置区段3发生短路故障，则由图6可知未发生畸变的故障监测信息为[1 1 1 0-1-1 0-1-1 0 0 0-1-1-1 0-1]。

图6 配电网算例模型Fig.6 Model of an example of distribution network

设置M5发生类型6的信息畸变，即-1畸变为1；同时设置M15发生类型5的信息畸变，即-1畸变为0。则发生畸变后的故障监测信息为[1 1 1 0 1-1 0-1-1 0 0 0-1-1 0 0-1]。

首先对网络进行分区，即图6中所示区域1～3。将其分支结构进行等效，得到如图7所示的外层等效模型。

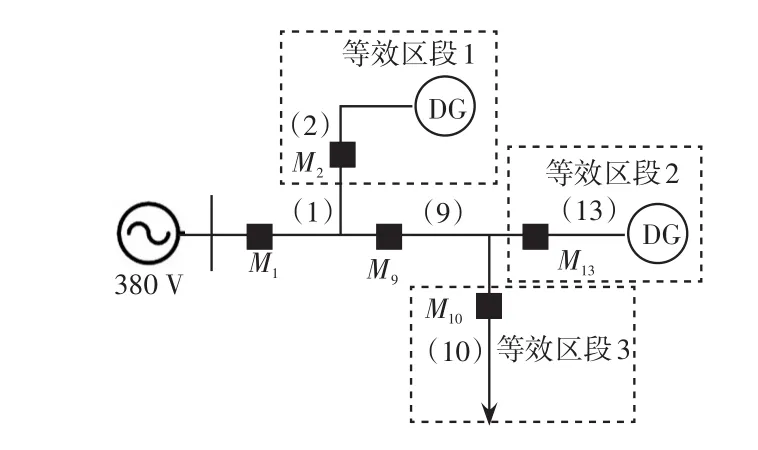
图7 外层等效模型Fig.7 Outer equivalent model

由图7可知，经过分支等效后，节点数及区段数由17减小为5。外层等效监测信息为[1 1-1 0-1]。采用第1节提出的故障定位算法进行外层求解，得出的优化结果为

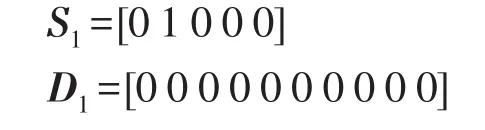
由S1可知，等效模型中第2个区段，即等效区段1发生了故障，由于等效区段1的分界节点M2监测信号为1，因此可将外层等效为电源以进行内层求解，其模型如图8所示。

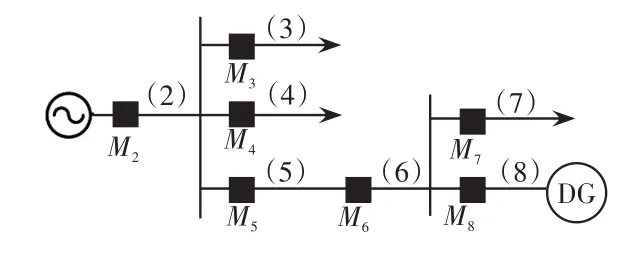
图8 内层等效模型Fig.8 Inner equivalent model

内层等效监测信息为[1 1 0 1-1 0-1]，采用定位算法得出的优化结果为

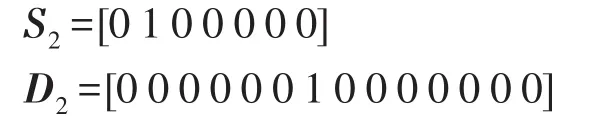
由S2可知故障段为等效区段中的第2段，即图6中的区段3，与设置结果一致。由D2可知等效区段中的第4段，即图6中的区段5发生信息畸变，与设置结果一致。由于区域2中的信息畸变对定位结果无影响，因此未对其进行识别。

由以上分析可知，本文所提方法通过故障定位算法分层求解能够有效实现低压配电网的故障定位，并且具有较好的畸变识别能力。

3.2 不同方法性能比较

为验证本文所提方法相对于其他方法的优点，本文在图6所示模型中设置不同故障位置，不同畸变位置，将未分层、计及畸变的直接求解法（方法1）、未计及畸变的分层求解法（方法2）、计及畸变分层求解法（方法3，本文方法）进行对比。对比结果如表2所示。

表2 故障定位结果比较Tab.2 Comparison among fault location results

分析表2可知，未分层的方法1变量维度为3N=51，由于维度过高，BPSO算法无法搜寻到正确结果，造成方法1的定位误差较大。分层后的方法2外层求解维度为15，内层3个区域的维度分别为21、15、9，维度降低，定位结果精度较方法1有较大改善，但由于未考虑畸变，定位结果依然有一定误差。本文提出的计及畸变分层求解法（方法3）在多点故障多点畸变的情况下保持了较好的性能，故障定位准确率较高。

为了进一步验证本文方法相对于文献[13]及文献[14]所提方法的优势，针对同一故障及畸变类型，表3给出了3种方法在定位准确率和总体求解时间方面的比较。

由表3可知，由于文献[13]基于信息矛盾原理处理畸变信息，容易出现误判，造成准确率定位不高，同时由于其需要两两对比相邻故障信息以检测畸变信息，导致其求解效率较低。文献[14]将配电网每条支路等效为二端口，以实现分层求解，但应用于多分支且分支较短的低压配电网时，减小变量维度的效果有限，定位准确率低于本文所提方法。综上，本文方法相对于以上两种方法具有更好的综合性能。

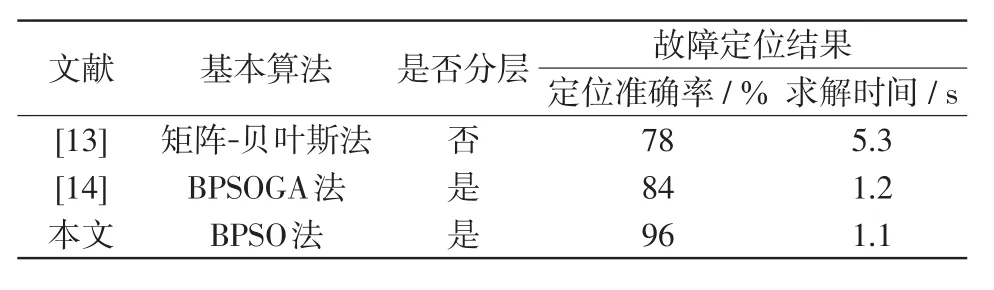
表3 不同方法性能比较Tab.3 Comparison of performance among different methods

4 结语

本文提出了计及信息畸变的低压有源配电网故障定位方法，依据信息畸变模型推导了故障定位目标函数，建立了计及信息畸变的故障定位模型，设计了模型分层求解方法进行模型分解，有效降低了模型求解变量维度。仿真算例表明，在发生多点故障、多点信息畸变的情况下，本文所提方法依然能够实现故障区段的精确定位，并且可识别出畸变点的具体位置。同时相对其他故障定位方法具有定位准确率高和总体求解效率高的优点。