均匀流作用下双柔性异管径立管响应特性试验研究

张智奇，任浩杰，付世晓，张萌萌

（1.上海交通大学a.海洋工程国家重点实验室；b.船舶海洋与建筑工程学院，上海200240;2.高新船舶与深海开发装备协同创新中心，上海200240）

0 引 言

海洋立管系统是连接海底井口与水面平台的唯一通道，约占整个油气开发系统总造价的1/4～1/3。海洋立管结构的安全性至关重要，立管一旦发生破坏，将会造成严重的经济损失和环境灾难。随着海洋油气开发不断向深水推进，用于连接顶部浮体与海底的各种管线结构也变得更加细长。在洋流作用下这种管线结构的两侧将产生交替涡泄，进而在其周围产生周期性的压力脉动；当这种周期性变化的载荷与细长管线结构的某一阶固有频率较为接近时，就会诱发其产生明显振动，这种振动即被称为“涡激振动”。研究表明，立管的涡激振动是其疲劳损伤不可忽视的因素。目前，国内外学者对单管涡激振动响应特性和水动力特性已开展了大量的试验和数值研究[1-2]，一定程度上提高了人们对立管涡激振动机理的认识。然而实际海洋工程中，多数情况下立管以集束形式存在，立管排列形式分为并列、串列和交错三种常见形式。相对孤立立管涡激振动，洋流流经集束立管时，立管之间尾流相互干扰，使其表面的分离点、旋涡脱落、表面压差及周期性受力等都与孤立立管存在显著差别。以三种常见排列形式为例，对于并列排列立管，立管之间尾流区可能存在相互叠加形成的交互作用，导致涡激振动特性发生显著变化；对于串列排列立管，下游管处于上游管尾流场中，受尾流干涉效应影响，上游管涡旋消散和下游管表面流动分离会发生改变，进而上下游管所受升、阻力会不同于孤立立管。交错排列立管，受上述尾流叠加和尾流干涉效应的共同影响，可能会表现出更加复杂的特性。立管集束群尾流干涉效应使得立管涡激振动特性变得极为复杂，可能会进一步加剧立管损伤，缩短立管服役期限，已成为近年来国内外工业和学术界研究关注的焦点。除此之外，在海底井口维护时，较小管径的生产立管旁排列大直径隔水立管的布置形式无可避免。相异水动力外径进一步加剧了立管涡激振动响应特性的复杂性，探究此种情况对立管产生何种影响，是目前海洋工程界无法回避的重要工程问题。

立管干涉研究中需考虑涡激振动（VIV）、遮蔽效应和尾流诱导振动（WIV）的影响。其中遮蔽效应是指位于来流前方的立管对后方立管的“遮挡”，使后方立管受到的流场拖曳力减小的现象。而尾流诱导振动（WIV）是指位于后方的立管由于前方立管泄放的漩涡作用激发的振动[3]。一般尾流诱导振动表现为随着流场流速（约化速度）增大，振动幅值持续增大。而涡激振动只在一定约化速度下才表现出强烈的振动幅度[4]。由于涡激振动、遮蔽效应与尾流诱导振动的同时存在，使得干涉现象复杂多变，对其机理的研究也更具挑战性。目前，国内外学者对尾流干涉现象主要针对同管径并串列形式立管涡激振动响应特性、升阻力系数等方面开展研究。Huera-Huarte 等[5]开展了两个具有大长细比、低质量比的立管串列，间距在2D～4D（D 为圆柱体直径）的尾流实验，分析了尾流干涉下涡激振动幅值，频率和相位与孤立立管的不同之处；Assi等[6]开展了串列刚性圆柱体试验，其中上游管固定、下游管做自激振动，试验发现了间距比在2D～5.6D 时，下游管产生“驰振”现象；Brika 等[7]对比了一个完全弹性圆柱体在一个固定圆柱体尾流作用下的结果，间距从7D～25D；与单独管相比，锁振时下游管约化速度增大并且比单独管有更广阔的反应区域；Lin等[8]在水槽中对刚性圆柱体群进行试验，试验中监测柱群中一个圆柱体流致振动动态响应特性，试验分析不同流速、不同排列和固有频率变化对监测圆柱体振动的影响，结果显示圆柱体可能出现椭圆运动，即顺流向的响应频率和横流向响应频率相同；Rolf Baarholm 等[9]开展了串列柔性带螺旋抑制装置以及裸管间距比为5D～20D 尾流干涉试验，试验探究了间距变化、来流攻角对立管涡激振动响应特性以及抑制效率的影响；Hover 等[10]研究了一个上游圆柱体固支，下游圆柱体可以在横向自由振动的两圆柱体干涉，试验中两圆柱体的间距为4.75D，分别测量了振幅、曳力及升力系数；Huse[11]和Blevins等[12]基于湍流模型，通过实验与数值对比，提出了均匀流场下立管尾流场模型，并在立管干涉的数值分析中得到了广泛应用。

综上所述，对相异水动力外径立管尾流干涉效应的影响研究尚未见文献报道，相异水动力外径会对尾流干涉效应有何影响也尚不清晰。本文针对上述问题，以当前实际隔水管和生产立管为原型进行缩尺制作立管模型，开展间距比为3D～8D，雷诺数为5 000～10 000，并列、串列和交错三种布置形式的双管干涉模型试验。试验采用布拉格分布光纤采集立管表面应变信息，进一步通过模态分析法重构立管涡激振动位移响应。对比不同间距、排列形式上游管和下游管以及孤立立管在同一流速下的响应，对相异外径立管干涉影响规律进行了研究和分析。

1 试验装置简介

本次试验采用自主研发的强迫运动装置，带动双管系统在水池水面下匀速运动，来模拟均匀流作用下双管系统的动力响应。整体试验装置如图1 所示，立管模型顶端固定于顶部连接装置，底端固定于底部连接装置，强迫运动装置由电机驱动，进而可以带动连接装置和立管模型整体在水平方向匀速运动。

双管相对位置的调节由自主设计的连接装置完成，顶部与底部连接装置带有横流向及顺流向方向的可滑动滑轨及滑块，将立管模型A 放置于主管管位，并在试验过程中保持其位置不变，通过改变立管模型B的位置即可实现不同双管排列形式及间距的调节。

本次试验采用的柔性立管模型部分物理特性及预张力施加大小都是根据实际工程中隔水立管（对应模型A）及生产立管（对应模型B）采用缩尺比λ= 19 换算得到的。最终制作的模型保证了立管模型水动力直径、干重及预张力满足缩尺比例要求。具体数值如表1所示。

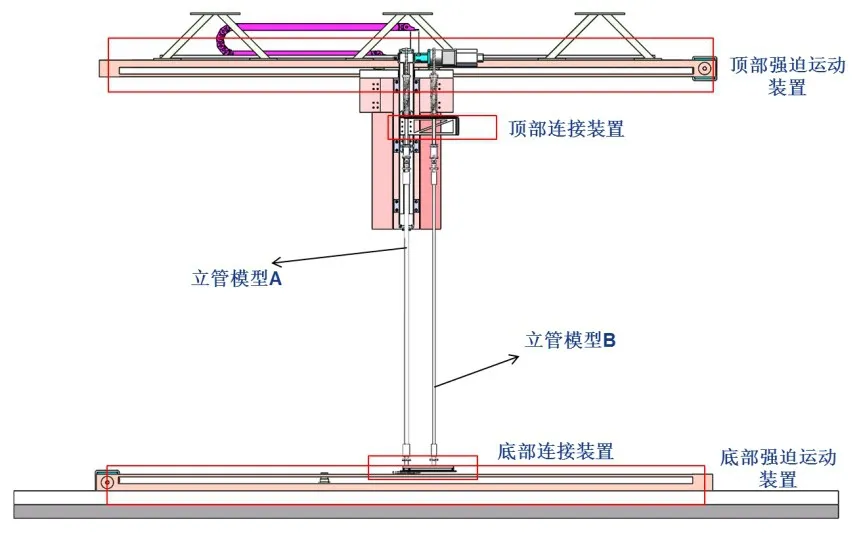
图1 试验装置整体示意图Fig.1 Experimental device

表1 立管模型参数Tab.1 Riser model parameters

试验中双管相对位置可划分为：并列形式、45°角交错形式和串列形式。如图2所示，串列形式与交错形式中根据立管处于流场中的相对位置，可分为上游立管和下游立管，其中处于来流方向前端的为上游立管，处于后端的为下游立管。试验中，针对立管A 为上游管，立管B 为下游管，以及立管B 为上游管，立管A 为下游管两种情况都进行了研究分析。并列形式双管壁面间距分别取3D、4D、5D，其中D 为参考直径，取D=17 mm。交错形式双管壁面间距分别取3.5D、4D、5D。串列形式壁面间距取3D、4D、5D、8D。流场流速0.3 m/s，对应立管A 雷诺数约8 500，立管B 雷诺数约5 400。试验中，两根立管均采用顶端铰支底端固支的形式连接。

本次试验采用分布光纤测量立管表面应变信息，立管A 及立管B 横流向和顺流向沿管长方向光纤光栅点布置如图3所示。

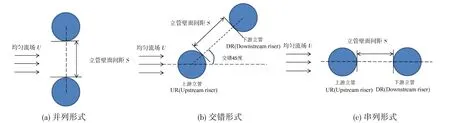
图2 双管布置形式示意图Fig.2 Schematic diagram of double pipe layout

图3 光纤光栅测点布置示意图Fig.3 Layout of fiber grating measuring points

2 数据分析方法

立管发生涡激振动时，圆柱体轴向应力由于周期性涡激振动而发生周期性的变化，因此立管光纤应变传感器所测得应变信号主要包括两个部分：动态变化的由轴向张力引起的轴向应变和由涡激振动产生的弯曲应变。立管表面横流向测点CFa和CFb关于中性轴对称。由小变形梁弯曲理论可知，由张力引起的轴向应变大小相等，方向相同，而由涡激振动引起的弯曲应变大小相等，方向相反。则CFa和CFb处的应变可表示为

式中，εCFa和εCFb分别为CFa和CFb所测得应变信息；εbend代表涡激振动引起的弯曲应变；εT代表轴向力引起的轴向应变。

由式（1）和（2）可得CF方向的弯曲应变

根据小变形梁弯曲振动理论，梁在时变载荷作用下的响应可以由不同级数与振型的乘积之和表示：

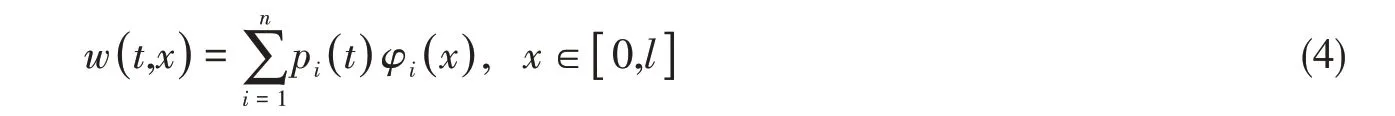
式中，φi( x )为柔性立管的第i阶模态振型；pi( t )为立管轴线流向第i阶位移的模态权重（Modal weight）；w( t,x )代表位置x处时间t时位移响应；l为管长。基于小变形假设，柔性立管的曲率可表示为位移对空间的二次导数：

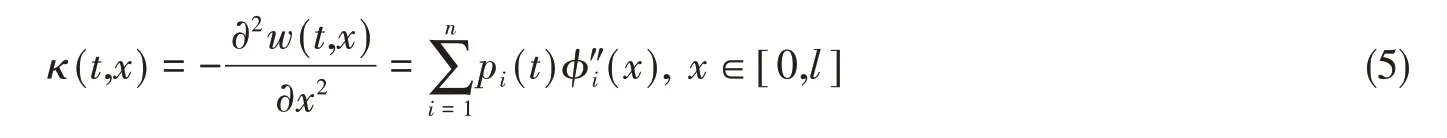
式中，φ″i(x)为柔性立管的第i阶曲率模态，立管的曲率和弯曲应变之间的关系，可表示为

式中，R为柔性立管的水动力半径，将式（5）代入式（6）可得应变响应和位移响应的关系：

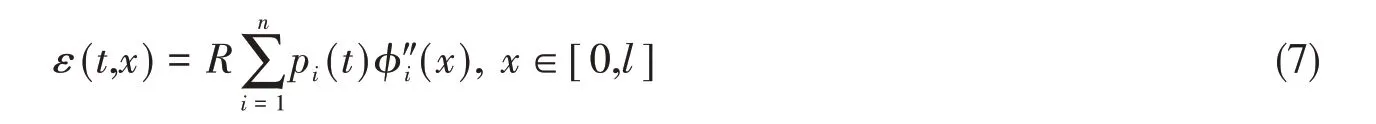
由式（7）可以看出，当测点的弯曲应变以及曲率振型已知，即可求出柔性立管各阶位移响应的模态权重pi(t)，继而由式（4）可得立管涡激振动的位移响应。

对于一端铰支和一端固支的立管，本文采用有限元数值软件Orcaflex 计算求解立管A 及立管B前五阶固有振型及固有频率，计算模型采用试验工况实际物理特性和预张力值，附加质量系数0.1，并考虑立管重力与浮力的影响。计算结果如图4及表2所示。

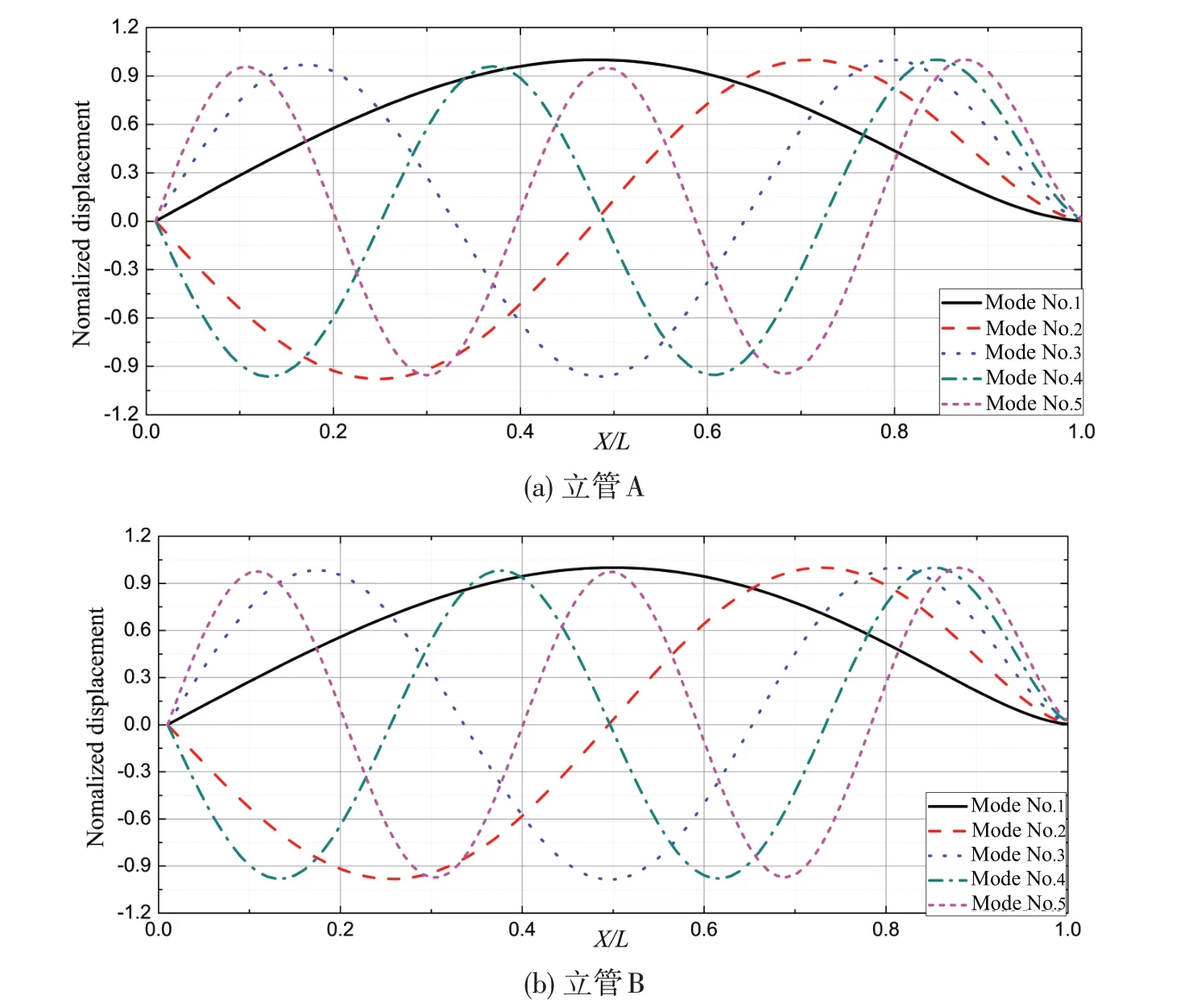
图4 一端铰支一端固支立管归一化振型Fig.4 Normalized displacement mode shapes for the riser with one end hinged and the other fixed

表2 固有频率Tab.2 Natural frequencies

为验证上述数据处理方法得到结果的正确性，这里取并列形式、双管壁间距4D 的试验工况处理得到的位移时历数据，通过立管弯曲应变计算公式如式（5）-（6），得到各测点应变值，与试验过程通过光纤光栅传感器测量得到的应变值做比较。对比结果如图5所示，可以看出处理得到的位移结果对应的应变值，与试验测得的应变值，沿管长方向一致，试验数据处理结果可靠。

图5 测量应变与计算应变比对Fig.5 Comparison between measured strain data and calculated data

3 分析与讨论

本章分析了各种布置形式及双管间距下，运动稳定时段内横流向整管位移RMS值和振动频率，以及立管横截面处涡激振动位移轨迹，和顺流向整管位移最大值。

3.1 横流向幅值特性与频谱分析

图6～10 为各布置形式下立管A 与立管B 横流向位移沿管长方向的分布曲线图，横坐标X/L 表示沿管长方向归一化位置点，左端为立管铰支顶端，右端为固支底端。纵坐标Disp/D表示各点位移与直径之比，即无量纲位移。位移分布图右侧附有各间距下立管响应频谱图（单管情况下，立管A与立管B频谱仅于并列布置形式中给出）。

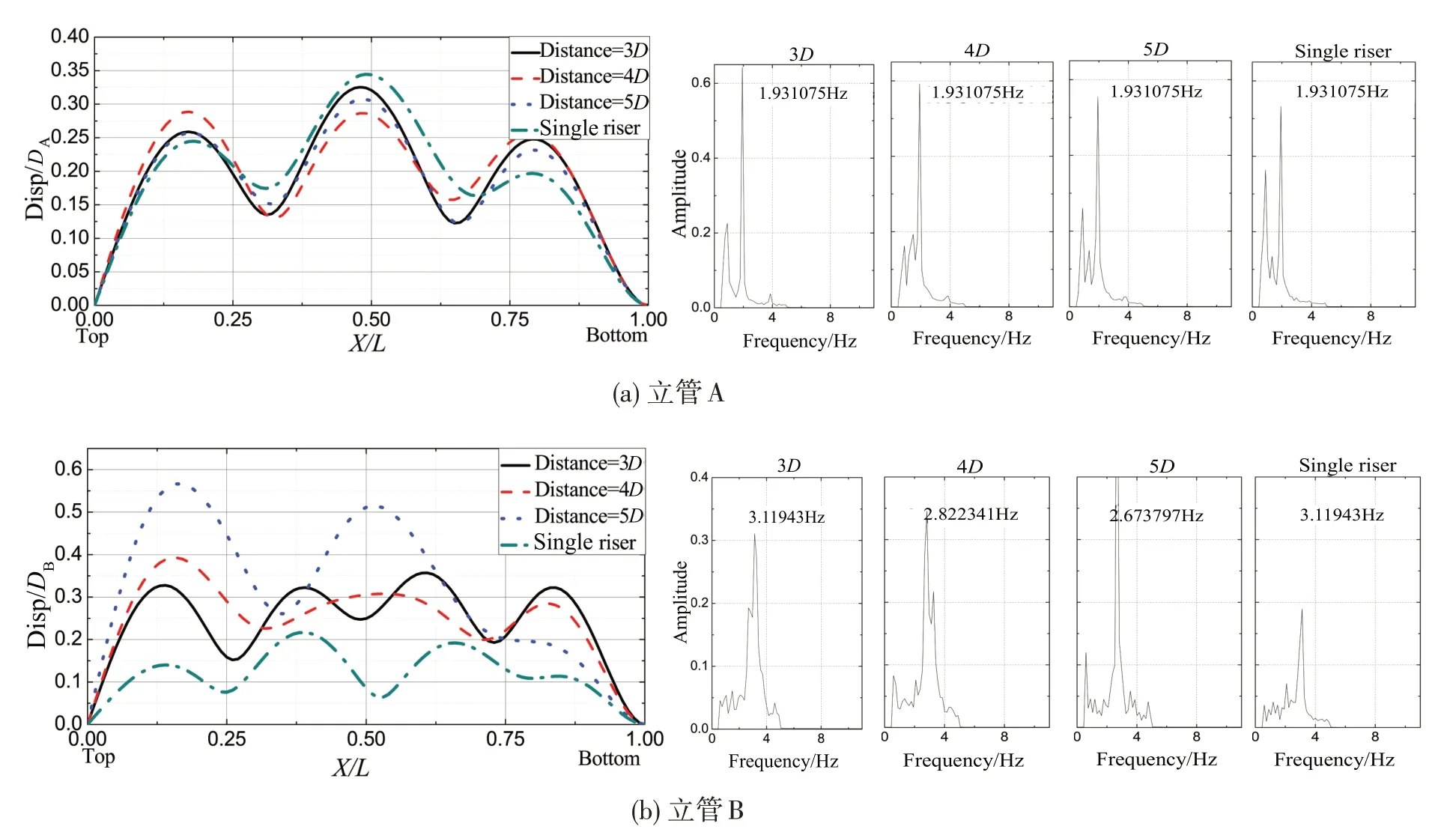
图6 并列形式横流向位移RMS值与频谱比较Fig.6 Comparison between cross flow RMS displacement and frequency spectrum in parallel form

由图6 可以看出，双管并列形式下，立管B 由于受到立管A 的干涉影响，振动位移RMS 值较单管时有所增大。当由单管变化到并列间距5D 时，整管位移RMS 值最大值分别为0.22DB、0.33DB、0.4DB、0.58DB，呈递增的关系。并且立管B 振动模态也发生显著改变，由单管及并列间距3D 时的四阶振型，变为并列间距4D和5D时的三阶振型。由频谱图也可以看出并列间距为4D和5D时，立管B振动频率发生改变，频率有所减小。而立管A 在并列形式下几乎没有受到立管B 的干涉影响而发生响应特性的改变。分析原因，可能是立管A 外径较大，因此其影响范围较大，而立管B 的外径较小，其影响范围也相应较小。根据Huera-Huarte[13]进行的双管并列试验结果给出的参考值，并列方向上立管的影响范围约为距离中心3.5DR（DR为产生影响的并列立管的直径），对应本文试验中立管A的影响范围为4.4D（D为本文试验的统一参考直径），立管B的影响范围为2.35D。本文试验结果显示，立管A在壁间距为5D 时仍对并列管产生影响，作用范围略大于Huera-Huarte 给出的参考值，而立管B 在壁间距为3D 时对并列管不产生影响，基本符合Huera-Huarte的试验结果。

图7 串列形式横流向位移RMS值与频谱比较，立管A（上游）Fig.7 Comparison between cross flow RMS displacement and frequency spectrum in tandem form,Riser A as UR

图8 串列形式横流向位移RMS值与频谱比较，立管B（上游）Fig.8 Comparison between cross flow RMS displacement and frequency spectrum in tandem form,Riser B as UR

由图7 和图8 可以看出，串列形式下，上游立管与下游立管间的干涉影响非常明显。下游立管受上游立管干涉影响振动幅值明显增大，振动模态也发生明显改变。同样，上游立管受下游立管干涉影响振动幅值增大，振动模态也发生明显改变。

根据频谱图可以看出，当立管A 作为上游立管，立管B 作为下游立管，在间距3D、4D、5D 时，两管产生同频率振动，并且随着管间距的增大，位移RMS值幅值逐渐减小，而当立管B作为上游立管，立管A 作为下游立管时没有发生同频率振动，并且振动RMS 值幅值不随间距的增大而发生变化。可以判断当立管A 作为上游管时发生了尾流诱导振动，并且随着间距的增大，尾流作用产生的响应逐渐减弱。而当立管B作为上游管时，同样对下游管产生一定的干涉影响，但只表现为下游管振动频率的减小，下游立管受尾流影响，但依然由涡激振动主导，因此振动RMS 值不发生显著变化。由此也可以看出直径较大的立管对后方尾流中的立管在横流向影响更大，这与Bokaian 等[14]进行的不同直径刚性柱体干涉试验得到的结果相一致。

串列形式下，下游管对上游管的干涉影响也很明显，并且当立管B 作为下游管，间距增大到8D时，上游管的振动RMS值就基本不受干涉影响。而当立管A作为下游管，间距为8D时，对下游管的干涉影响依然很明显。可见直径较大的立管对其前方的立管在横流向影响同样更大。

图9 45°交错形式横流向位移RMS值与频谱比较，立管A（上游）Fig.9 Comparison between cross flow RMS displacement and frequency spectrum in staggered form,Riser A as UR

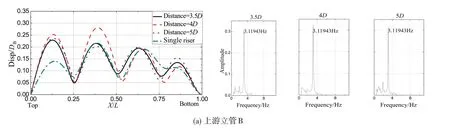
图10 45°交错形式横流向位移RMS值与频谱比较，立管B（上游）Fig.10 Comparison between cross flow RMS displacement and frequency spectrum in staggered form,Riser B as UR

由图9 和图10 可以看出，双管交错形式下，作为上游管的立管基本不受下游管的干涉影响，而下游管明显受到上游管对其产生的干涉影响。当立管A 作为上游管，立管B 作为下游管，双管间距3.5D，4D 和5D 时，振动模态由单管时的四阶变为三阶，响应的频率也有所减小，位移RMS值均有所增大，但此种情况下的下游立管B没有产生与上游立管相同频率的振动，因此可以判断交错形式下下游管同时含有涡激振动及尾流诱导振动的成分。并且由于尾流的作用，振动幅值有所增大。同样，当立管B 作为上游管，立管A 作为下游管时，由于干涉的影响，立管A 振动模态由单管时的三阶变为二阶，响应的频率也有所减小。位移RMS值最大值由单管时的0.35DA，变为0.45DA。

3.2 立管横截面位移轨迹分析

图11～15为各布置形式下，立管稳定运动时段内运动响应较明显截面处的运动轨迹图。其中X轴表示横流向方向，Y轴表示顺流向方向。

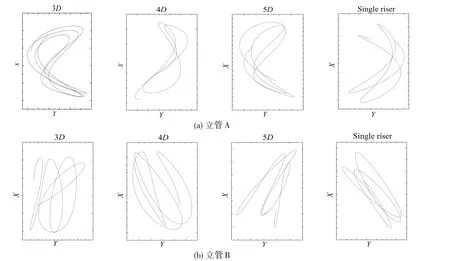
图11 并列形式立管横截面位移轨迹Fig.11 Motion trajectory at cross section of riser in parallel form

由图11 可以看出，并列形式下，立管A 横截面运动呈显著的8 字形，说明立管A 的涡激振动稳定显著，受并列立管干涉影响很小。而立管B 在干涉影响下，运动轨迹变得混杂无序，此时立管B 受到复杂的流体激励力，而不是典型的涡激振动。

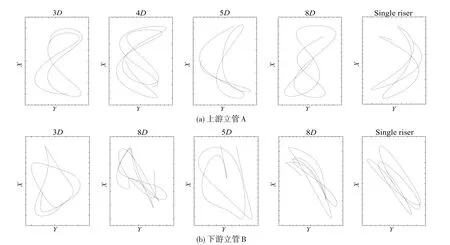
图12 串列形式立管横截面位移轨迹，立管A（上游）Fig.12 Motion trajectory at cross section of riser in tandem form,Riser A as UR

图13 串列形式立管横截面位移轨迹，立管B（上游）Fig.13 Motion trajectory at cross section of riser in tandem form,Riser B as UR

由图12 和图13 可以看出，串列形式下，位于尾流中的下游管受到尾流的干扰，运动轨迹杂乱无章，而上游立管基本保持稳定有序的运动轨迹，作为上游管的立管A 位移轨迹呈现8 字形，而作为上游管的立管B位移轨迹呈现椭圆形。因此可以看出串列形式下，上游立管涡激振动响应稳定显著，而下游立管受到尾流激励力和自身泄涡激励力共同的作用，并且这种作用力非常不稳定。

当串列间距为3D 时，上游立管B 同样发生了运动轨迹的改变，呈现出8 字形运动轨迹，说明在间距较小时，上游立管B同样会受到下游立管A的干涉影响。

图14 45°交错形式立管横截面位移轨迹，立管A（上游）Fig.14 Motion trajectory at cross section of riser in staggered form,Riser A as UR

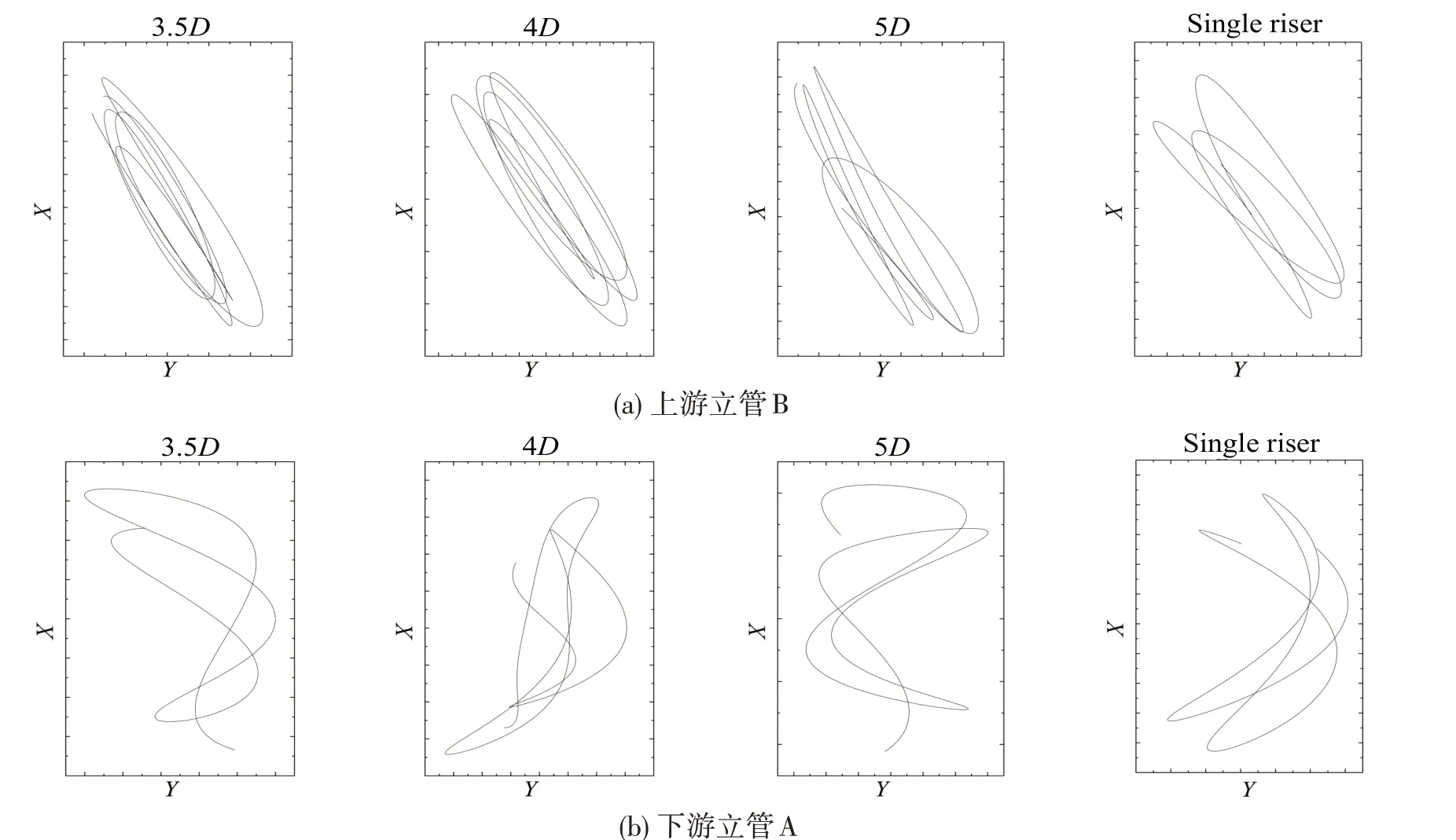
图15 45°交错形式立管横截面位移轨迹，立管B（上游）Fig.15 Motion trajectory at cross section of riser in staggered form,Riser B as UR

由图14 和图15 可以看出，交错形式下下游立管B 在间距为3.5D 时运动轨迹较混杂，斜间距为4D、5D时椭圆形轨迹稳定，而下游立管A在间距为4D时运动轨迹混乱无序，在间距为3.5D、5D时都为较稳定的8字形运动。可以看出不同直径的上游立管对下游立管的影响范围也有所不同。只有当下游立管处于上游立管尾流场中某些特定位置点时，才会受到上游立管显著的干涉影响，破坏其稳定的运动位移轨迹。

3.3 顺流向位移最大值分析

图16为不同布置形式、不同间距下顺流向位移最大值分布点线图，其中横坐标S/D代表壁间距与参考直径比值，纵坐标Disp/D 表示位移最大值与直径之比，每条点线代表不同的布置形式，分别为单管、串列形式中的下游管、交错形式中的下游管、并列形式中的并列管、交错形式中的上游管，以及串列形式中的上游管。

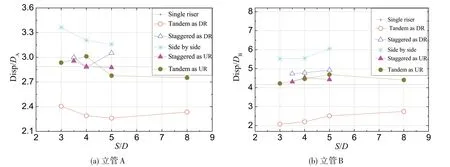
图16 顺流向位移最大值比较Fig.16 Comparison of in-line flow max displacement

由图16 可以看出，并列形式下，立管A 和立管B 在干涉影响下顺流向位移都有所增大，但立管A的响应变化较小，最大位移均值在并列间距3D时出现，比单管情况下多出0.5DA，而立管B最大位移均值出现在并列间距5D时，比单管情况下多出2DB。并且当并列双管间距增大时，立管B位移均值逐渐增大，这与此种布置形式及间距下立管B横流向位移变化规律一致。

交错形式下，上游立管和下游立管均受干涉影响，顺流向位移均值有所增大，但变化幅度很小，只有在立管B 作为下游管时，受立管A 干涉影响位移均值最大值由单管的4.2DB变为5DB。由于顺流向位移没有减小，反而增大，因此交错形式这些间距位置下上游立管没有对下游立管产生遮蔽效应，而使其位移增大的原因可能与并列情况下立管顺流向位移增大的原因是一样的。

对比所有布置形式，串列形式下由于遮蔽效应的影响，下游立管位移减小最明显，并且这种影响在壁间距为8D 的情况下，依然很明显，这与许多其他串列干涉实验的结果相吻合，如Bokaian 等[15]的实验结果。Bokaian 等在实验中同样对上游立管的位移响应进行了研究，结果显示在双管间距很小时，上游立管受到的拖曳力有所减小，位移也相应减小，但本次试验中上游立管的位移出现增大的现象，此时两管顺流向间距最小，极易发生碰撞。可以看出存在其他因素会对上下游立管周围的流场形态产生影响，而具体作用机理需要进一步探索。

4 结 论

通过顶端铰支底端固支、不同直径的双立管模型干涉试验得到的数据结果，分析比较两立管在不同相对位置以及不同流速均匀流流场作用下的响应特性，得到如下结论：

（1）并列形式下双管间干涉影响范围与直径大小有关，立管A 的影响范围大于壁间距5D，而立管B 的影响范围小于壁间距3D。由于并列立管A 干涉的影响，立管B 横流向位移RMS 值及顺流向位移最大值均有所增大。并且当并列双管间距增大时，横流向位移RMS 值和顺流向位移最大值逐渐增大。而且由于受到复杂不稳定的流场作用力，立管B的截面运动轨迹也呈现混乱无序的形态；

（2）与其他布置形式相比，串列形式下两管干涉影响最大，处于尾流场中的下游立管受遮蔽效应影响顺流向位移减小显著，并且在本次试验中流场流速为0.3 m/s，立管A为上游立管，双管间距3D和4D，立管B 为上游立管时，在双管间距3D、4D、5D、8D 下，上游立管出现了位移增大的情况，此种情况下两立管最易发生碰撞，工程实际应用时应避免此种情况的发生；

（3）试验过程中，当立管A 作为上游立管时，下游立管B 发生尾流诱导振动（WIV），与上游立管产生同频率振动，并且随着两管间距的增大，振幅逐渐减小。而当小直径立管作为上游管时，没有对下游管作用产生尾流诱导振动，下游管以涡激振动主导，此时随着两管间距的增大，振幅不发生改变；

（4）交错形式下，下游立管受上游立管尾流的影响，振荡频率有所减小，振荡幅值增大，此种情况下下游立管受到涡激振动（VIV）及尾流诱导振动（WIV）的共同作用。当立管A 为上游管时，立管B 只有在间距为3.5D时所受到的流场作用力才会变得不稳定，当立管B作为上游管时，立管A只有在间距为4D 时才会受到不稳定的流场力作用，说明处于尾流场内的立管，受到的尾流作用力和涡激振动力在不同位置处可能是稳定的，也可能是不稳定的，而不同直径的立管具体的尾流场特性也不同。