由数列递推关系探究通项公式
———2020年全国卷Ⅲ数列题的解答
◇ 云南 周必辉
数列因规律性强、题型多样、方法灵活等特点,成为高考命题的重点,其中给出递推关系求通项公式问题是有效考查考生化归转化能力、推理论证能力的重要题型.本文以2020年全国卷Ⅲ数列解答题为例,探究根据递推关系求通项公式的方法.
1 考题说明
例(2020年全国卷Ⅲ)设数列{an}满足a1=3,an+1=3an-4n.
(1)计算a2,a3,猜想{an}的通项公式并加以证明;
(2)求数列{2nan}的前n项和Sn.
数列的递推关系在人教版教材中虽然是以选学内容出现,但在高考中以递推关系为背景的命题却屡见不鲜.本题第(1)问考查考生根据递推关系求通项公式,所给的递推关系类型是an=Aan-1+f(n).下面对这类问题的求解方法进行总结,并应用这些方法解答此题.
2 解法综述
根据不同的递推关系类型,常用的解题方法主要有如下4种.
1)叠加法
对于an-an-1=f(n)的形式,可利用叠加法求通项公式,即an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=f(n)+f(n-1)+…+f(2)+a1.
2)叠乘法
3)构造法
此方法适用的类型较多,构造的原理是将所给的递推关系进行变形,将其构造为等差数列或等比数列的形式.
4)归纳法
通过观察数列前几项,猜想出其通项公式,再进行证明.
3 问题解答
在某些问题的求解中,往往需要综合应用多种方法.本题第(1)问旨在考查利用归纳法求通项公式,下面从多种视角进行解法探究.
解析
方法1由a1=3,an+1=3an-4n,可得a2=3a1-4=5,a3=3a2-4×2=7,a4=3a3-4×3=9,猜想an=2n+1.
证明:当n=1时,a1=2×1+1=3.设当n=k时,ak=2k+1,则当n=k+1时,ak+1=3ak-4k=3(2k+1)-4k=2(k+1)+1,所以{an}的通项公式为an=2n+1.
点评
应用此方法求数列的通项公式时,要准确识别条件中隐含的关系,平时学习中要注意积累一些特殊的关系,如奇数、偶数、正整数的平方与立方等.
方法2将an+1=3an-4n两边同时除以3n+1,得,即进而由叠加法可得
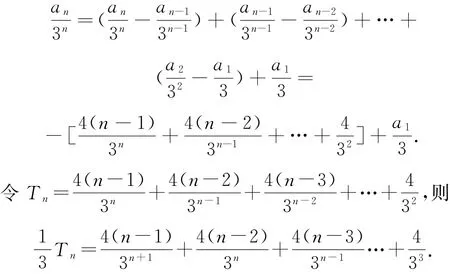
两式相减得
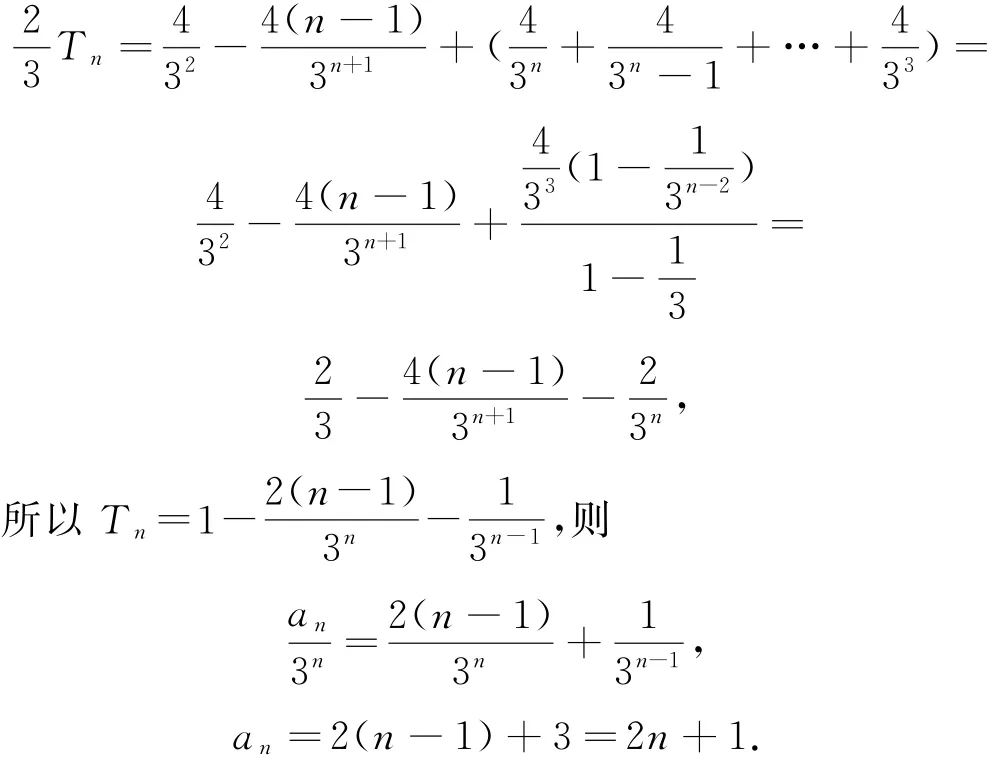
点评
本解法通过对所给递推关系进行变形,将其转化为可利用叠加法求解的形式,再利用错位相减法及等比数列的求和公式求得结论.
方法3设bn=an+λ n+μ,则an=bn-λ n-μ,代入an+1=3an-4n中,得bn+1-λ(n+1)-μ=3(bn-λ n-μ)-4n,即bn+1=3bn- (2λ+4)n+λ-2μ.
点评
本解法是通过待定系数法构造等比数列bn,而由已知可求得b1=0,所以{bn}为常数列,各项均为0,进而求得数列{an}的通项公式.
方法4由an+1=3an-4n,得an+2=3an+1-4(n+1),两式相减得an+2-an+1=3(an+1-an)-4.
令bn=an+1-an,则bn+1=3bn-4.
设bn+1+λ=3(bn+λ),即bn+1=3bn+2λ,由2λ=-4得λ=-2,所以数列{bn-2}的首项为b1-2=a2-a1-2=5-3-2=0,且知b2=2,所以{bn}为常数列,bn=an+1-an=2,即数列{an}是公差为2的等差数列,所以an=3+2(n-1)=2n+1.
点评
在得出an+1=pan+q(p≠0,q≠1)的递推关系后,可利用待定系数法,即引入参数λ,令an+1+λ=p(an+λ),将其展开后与原递推关系对照,求得λ值,从而构造{an+λ}为等比数列.
由第(1)问知an=2n+1,则2nan=(2n+1)2n,进而可利用“错位相减法”求其前n项和.第(2)问较为简单,在此不再赘述.
综上所述,给出递推关系求数列通项公式的过程其实就是转化的过程,即将一般化特殊、将陌生化熟悉.教学中我们只学了两类特殊的数列,即等差数列和等比数列,因此所求问题最终都要转化为与等差或等比数列相关的问题来求解.

