基于马尔科夫决策过程的混动汽车能量管理建模及控制策略
陈福云 花春梅
(江苏联合职业技术学院淮安生物工程分院,江苏 淮安 223200)
在实际中,虽然驾驶员的操作可测,汽车的速度和功率可测,但若传统的基于数据驱动的方法,如神经网络、 支持向量机、 决策树等,可获得的预测功率或车速为具体值,无法准确反映驾驶风格的随机性特征。而马尔科夫链由于其概率化表达,在后续求解过程中得到的策略可以满足概率性最优,更符合实际的车用动态化场景。马尔科夫过程是指控制模型中的状态量具有马尔科夫特性,即在已知上一时刻值的前提下,其当前时刻的值只与上一时刻的值相关,而与再之前的值无关。基于马尔科夫链的随机动态规划方法来解决随机负载功率下的混合动力驱动系统最优控制问题,利用值迭代和策略迭代获得了统计学意义上综合性能指标最优的控制律。
1 基于马尔科夫过程的HESS 能量优化管理建模
由于有限马尔科夫决策过程面向的是离散状态的系统,因此本文首先根据动力电池、 超级电容的状态方程/物理方程,对其进行离散化处理,并形成HESS 系统的状态迭代更新流程。
动力电池RC 网络端电压vp和SOC 的离散化迭代方程如下:

为方便后续统一化形式表达及矩阵运算,将式 (1) 改写为矩阵形式如下:

超级电容的离散化表达如下:
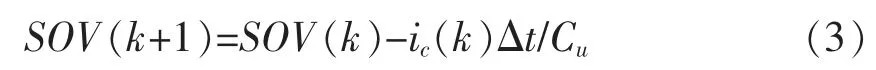
式中:Cu 表示超级电容的电容值,值为13.83F。
离散化模型式 (2) 和 (3) 均可以统一成如下形式:

式中:s(k)表示状态向量,对于动力电池系统,s(k)表示一阶 RC 网络端电压 vp和 SOC,对于超级电容,s(k)表示 SOV。
基于动力电池和超级电容的离散化模型、DC/DC 效率模型,可形成如下的HESS 系统状态迭代流程:
本文中,将 “需求功率-电池SOC-超级电容SOV” 作为系统联合状态,将电池电流作为动作(即控制变量,并且将电流的幅值设定在2C 倍率内,即控制电流的大小应该在-154A~154A),在已知状态量和控制量的前提下,可根据式 (2)更新电池的状态,根据下式计算电池的输出功率:

根据拓扑结构,DC/DC 转换器和动力电池串联,即两者共享相同的功率及电流 (不考虑线路中的功率损失),因此可假定DC/DC 转换器的电流和功率与电池完全一致,根据效率Map 查询插值获得DC/DC 转换器效率。
需求功率的剩余部分由超级电容补充,因此,超级电容的功率:

式中:表示动力电池和超级电容的联合效率,即。
联立超级电容的功率公式,可得到超级电容电流的计算公式如下:

最后根据式 (2) 更新超级电容状态SOV,至此完成动力电池-超级电动-DC/DC 转换器HESS 的状态量迭代更新。
2 基于马尔科夫决策过程的HESS 能量管理定义
定义马尔科夫决策过程的关键在于确定系统的状态、 动作、 TPM 以及回报。
2.1 系统的状态和动作
这里主要针对系统状态数量为有限值的情况进行讨论。考虑环境根据时间点t 时刻的动作在时间点t+1 时刻给出的响应,在任意泛化的场景下,该响应可能依赖于此前所有发生的记录,在上述场景中,系统的动态响应必须通过如下式(8) 所示的过去历史的所有可能值的完全联合概率分布表示:
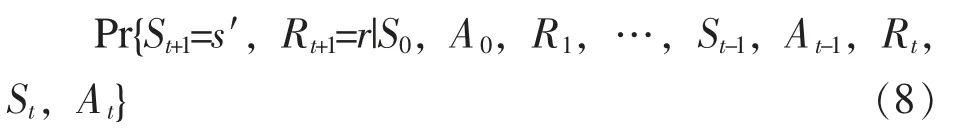
如果状态信号具有马尔科夫特性,那么系统在t+1 时刻的响应将完全依赖于t 时刻的状态和动作,那么系统的动态响应可以描述为:
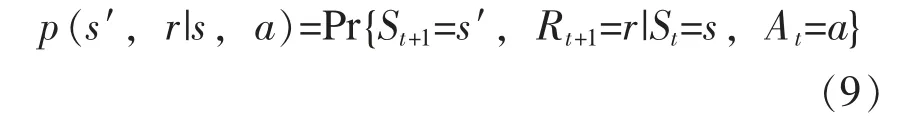
换而言之,当且仅当式 (8) 对所有的 s′、 r以及所有的历史信息都满足式 (9) 时,称系统的状态、 环境甚至控制问题具有马尔科夫特性。
2.2 马尔科夫决策过程
这里仅讨论状态量为有限数量的马尔科夫决策过程。马尔科夫决策过程的状态-动作对完全由环境的单步动态响应决定,即给定状态s 和动作a,系统下一时刻的状态s′以及回报r 将完全由式 (9) 确定,这就完全定义了有限马尔科夫决策过程。
基于式 (9) 描述的马尔科夫决策过程动态特性,可以计算关于环境的一切参数量,如对于某一状态-动作对应的期望回报可以表达为:

状态转移概率为:
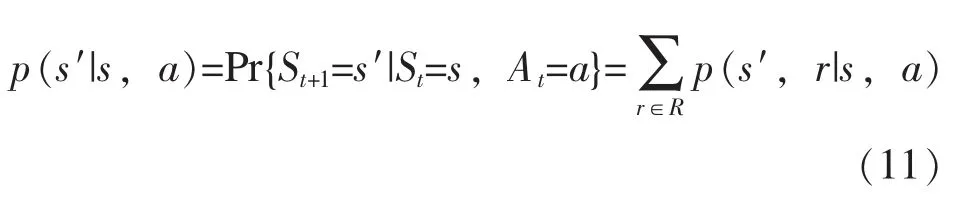
状态-动作-下一刻状态三元组对应的期望回报为:
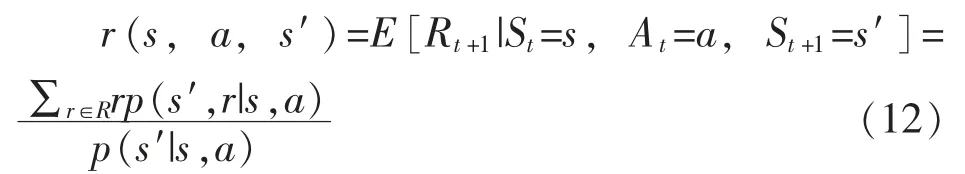
2.3 系统的TPM 以及回报
系统的TPM 可通过结合HESS 系统总模型和需求功率状态概率转移矩阵确定,定义系统的能量损失作为回报函数,即:

式中:z 为逻辑变量,当电池充电的时候值为1,当电池放电的时候值为0。另外考虑到系统平衡特性,如果下式 (14) 约束不能被满足时,额外惩罚将被纳入到回报函数中:
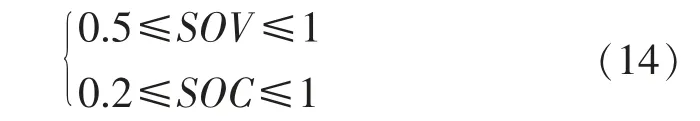
根据马尔科夫决策过程理论,最优解即寻找一个从状态到动作的最优映射使得状态的值函数可以取得最大值,即使下式 (15) 表示的累计回报函数取得最大值:

式中,由于马尔科夫决策过程通常是最大化累计回报,而本文中需要的目标是最小化能耗,因此在式 (15) 前增加了负号。
3 基于策略迭代的最优控制策略
为了应用基于有限马尔科夫决策过程的求解算法,即策略迭代算法,需要对问题中涉及的连续量进行离散化处理,这里对连续变量的离散度说明如下:需求功率的离散粒度为20kW,SOC和SOV 的离散粒度均为0.1,动力电池控制电流的离散粒度为4A。
基于上述连续变量的离散化处理后,根据策略迭代算法对建立的HESS 能量管理问题进行求解,获得不同功率等级场景下的控制策略Map如图1 所示,其中展示了需求功率分别为-20kW、20kW、 -140kW 和140kW 四种功率等级下从状态量到动作的映射。
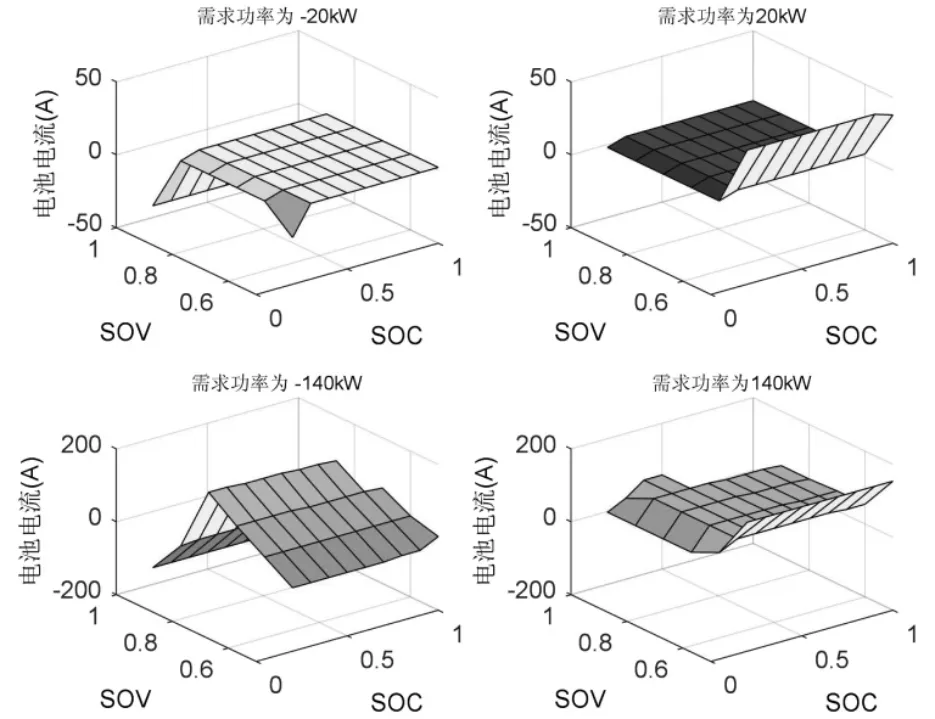
图1 基于策略迭代的最优控制策略Map
(1) 当需求功率为-20kW 时,在绝大多数情况下,电池电流为0,这说明此时超级电容将作为主要动作部件,对负功率进行能量回收。然而,当SOV 接近于1 时 (这意味着超级电容已接近满电,无法再储存更多的能量),电池电流变为负值,制动能量回收主要通过电池实现。
(2) 当需求功率为 20kW 时,超级电容仍然是主要的能量源,只有当SOV 非常低时,电池才会放电。
从 (1) 和 (2) 两种场景可以看出:当需求功率较低时,最优控制策略主要发挥超级电容的能量缓冲作用以满足小功率场景下的能量回收或输出。
(3) 当需求功率为-140kW 时,如果 SOV 很高,即超级电容无法再回收更多的能量时,此时动力电池负电流较大,主要由动力电池进行制动能量回收。另外,即使需求功率为负,当 SOV较低时,电池仍然可能工作在放电状态,这是因为此时电池倾向于给超级电容充电,从而保证其在小功率场景下的功率输出缓冲能力。
(4) 当需求功率为 140kW 时,电池成为主要动力源,如果超级电容的SOV 特别低,电池会增大放电电流,不仅提供负载所需功率,同时多余功率将用于超级电容充电。如果SOC 特别低,电池将减小放电电流,电池不能满足的功率需求将由超级电容补足。
从 (3) 和 (4) 两种场景可以看出:当需求功率较高时,将优先选用动力电池作为能量源,这是因为动力电池具有较大的能量密度;且在一定场景下,动力电池会提供多余功率用于超级电容充电,以保障超级电容的能量缓冲效果。
4 结束语
本文详尽介绍了基于马尔科夫决策过程的HESS 能量管理建模及控制策略。首先根据动力电池、 超级电容的状态方程/物理方程,对其进行离散化处理,并形成HESS 系统的状态迭代更新流程,即对HESS 能量优化管理建模。然后对马尔科夫决策过程进行了定义,根据HESS 的具体应用场景,定义了所研究的能量管理策略的马尔科夫过程基本要素即系统的状态、 动作、 TPM 以及回报,最后通过四种不同功率等级下的最优控制策略Map 阐述了控制策略的核心思想,即在考虑SOC 和SOV 约束的前提下,充分发挥超级电容的能量缓冲作用,同时利用动力电池大能量密度的优势。


