三自由度机械手雅可比矩阵的建立及动力学仿真

蔡玉强，张文瑞

三自由度机械手雅可比矩阵的建立及动力学仿真

蔡玉强，张文瑞

（华北理工大学 机械工程学院，河北 唐山 063210）

基于ADAMS的仿真技术，对工业机械手进行运动学和动力学仿真上的分析。对于三自由度工业拾取机械手，通过D-H方法[1]建立每个连杆的参考坐标系，首先研究了机械手的主要理论及数学基础，得到了机械手运动学的方程，给出抓取机械手的每个连杆与末端执行器之间的姿势关系，并推导出机械手的运动学方程，利用微分变化法获得雅可比矩阵。通过连杆间力和力矩的递推求得力雅可比矩阵以验证机械手建立的正确性。然后在ADAMS中对机械手运动进行仿真使用后处理模块，在各个关节处分别添加驱动函数，并验证了该机制的可行性。

机械手；三自由度；雅克比矩阵；ADAMS

近几年工业机械手的发展十分迅速，应用在各行各业。机械手技术是一种跨学科的综合技术，涉及到机械、力学、电气液技术、自动控制技术等领域[1-2]。机械手作为生产设备实现了完全的自动化。工业机械手结合了人机之间在结构和性能上的优势，特别体现了人的智能和适应能力。当前我国各个领域机械手的准确性和在复杂环境下工作都具有很好的发展前景。机械手目前仍需改进的是不如人的手灵活，但它不知疲劳、不惧危险，能持续不间断地工作，并且抓重物的能力大于人。

工业机械手要根据现场要求来操作，即通过某种执行机构在空间中移动零件或工具。这需要对加工零件、工具以及机构本身的位置和姿态进行表达。

1 运动学分析

在工业机械手整个工作过程中，应该给机器本身以及执行端部较大的工作空间，且使机械手对作用对象有良好的承载能力。在结构形式上，机械手具有刚性、简单的运动学正反解、机构件和末端的位置控制等特点。因此，机械手需要满足运动、位姿等方面的性能要求，同时在竖直方向上，应具有合理的动作空间和便捷的操作性以及避障空间，使机械手在正常运作过程中，达到每项指标上的完整度。依据所需要的功能要求，设计了三个转动关节机械手，如图１所示。

图1 机械手机构示意简图

机械手在空间的运动是每个杆件中的旋转和平移合成作用的结果。在这种思想的基础上，如果要想描述机械手的位置和姿态，就需要实现连续坐标变换矩阵。在计算各种机械手时，标准不统一使得计算方法较多、难以通用。

1955年，Denavit与Harenberg提出了机械手坐标系变换的D-H参数[4]，该方法系统化地解决了通用的问题，其需要4个参数来描述位置、方向与相邻坐标系的关系。这种坐标系变换表示法适用于所有具有串联结构的机械手，能解决其移动关节、旋转关节、合成运动等的运动学计算。这种表示法得到的矩阵方程，在形式上更加统一规范，便于进行研究。

机械手的正运动学模型，反映的是关节和执行端部之间的联系。为保证机械手末端位姿的正确求解，需要得到每个关节的精确角位移，因此采用D-H参数法，参数表如表1所示。

表1 D-H参数表

由表1中所示的连杆参数，可求得各连杆变换矩阵为：

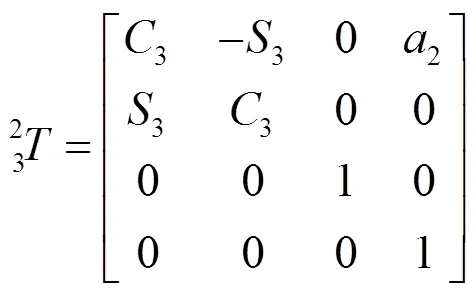
式中：C＝Cosθ；S＝Sinθ；左侧的0、1代表建立的坐标系0到1的位姿变换矩阵，1、2代表建立的坐标系1到2的位姿变换矩阵，以此类推。

求解各连杆在1＝2＝3＝0°下的位姿矩阵为：

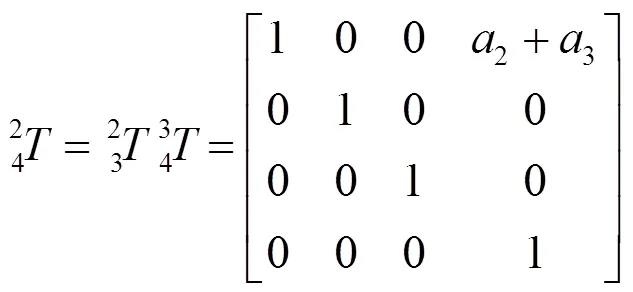
1.1 雅可比矩阵

如果要建立执行端与电动机之间的联系，显示二者间的动力学特性关系，需要映射机械手杆件的每个关节。为了实现此目的，首先需要在机械手的执行末端和每个关节建立联系，也就是对速度和加速度建立连接，这就需要建立机械手的雅克比矩阵。把系统动力学特性完全映射到机械臂上。

雅可比矩阵是机械手的工作空间与关节空间的动态参数之比，其行数表示操作空间的维数、列数表示机械手的关节数。本文研究的机械手其雅克比矩阵为3×3阶。

求解雅可比矩阵的方法通常有两种：一种是矢量积分法，另一种是微分变换法。本文研究的是串联机械手的结构特点，只有转动关节，不存在高阶求解的困难，所以两种求解方法皆可行。考虑到微分变换法计算量相对较小，这里采用微分变换方法。

机械手的雅可比矩阵可以将机械手的关节空间与操作空间的速度、力和力矩联系起来形成映射关系。即，机械手的雅可比矩阵主要是为了表达关节空间和操作空间之间的关系[5]。

机械手的雅可比矩阵，通常是指从杆件的运动空间到执行端的动作空间，有：

由于机械手全部为转动关节，所以微分变换法应使用：

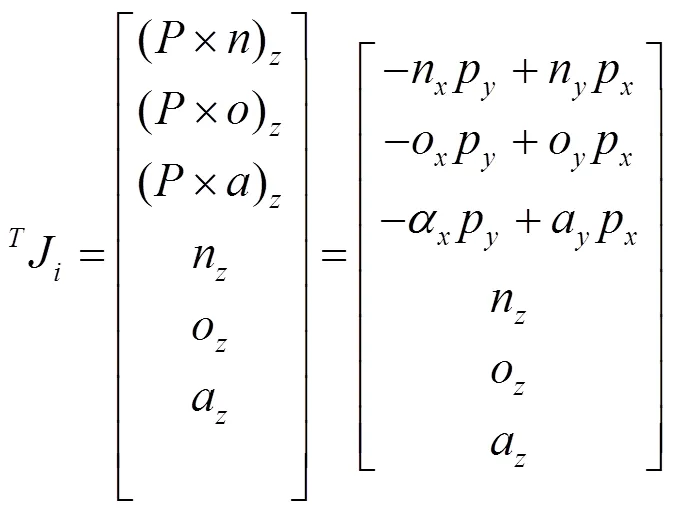
式中：J为每一列的雅可比矩阵；表示位姿矩阵1～4列的参数。

雅克比矩阵是相对于末端坐标系构建的，则有：

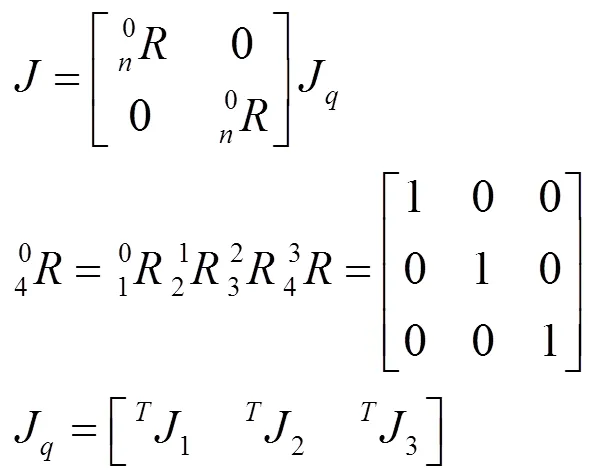
式中：为变换矩阵的前三行三列矩阵；J为基端坐标系的雅可比矩阵。

对于三连杆的操作臂，可以写出一个3×3的雅克比矩阵，该矩阵将关节速度和末端执行器的速度联系起来，解得雅克比矩阵为：

1.2 奇异性分析

多数操作臂都有使雅克比矩阵出现奇异的值。所有操作臂在工作空间的边界都存在奇异位形，且多数操作臂在其工作空间内也有奇异位形。当2为0或180°时，机构处于奇异位形。从物理意义上讲，当2＝0时，操作臂完全展开，处于这种位形时，末端执行器仅可沿坐标的某个方向运动，即失去了一个自由度。同样，当2＝180°时，操作臂完全收回时，手臂也只能沿着一个方向运动，而不能在两个方向运动。由于这类奇异位形处于操作臂工作空间的边界上，因此称其为工作空间边界的奇异位形。

1.3 力雅克比矩阵求解

机械手在作业过程中，各关节产生相应的作用力。由机械手每个关节的驱动装置提供的关节力，通过连杆传递到执行端，并克服外界作用力。

机械手的末端执行器受到外载荷作用，各关节的驱动力（矩）通过连杆传递到末端执行器，从而克服外界作用力（矩）。

该机械手是由各个连杆和各种关节相连接组成，把其中一个连杆作为静力分析的对象。连杆及相邻连杆－1间的作用力和作用力矩关系，如图2所示。

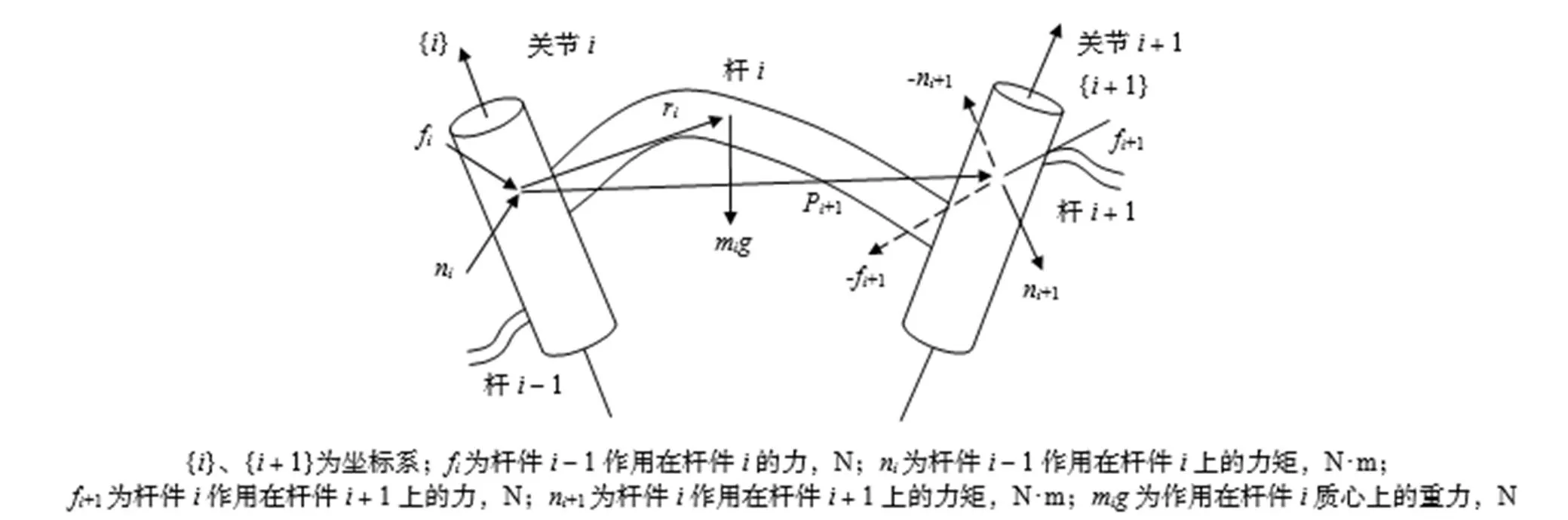
图2 邻杆之间力和力矩关系

连杆的力和力矩平衡方程在坐标系{}中表示为：

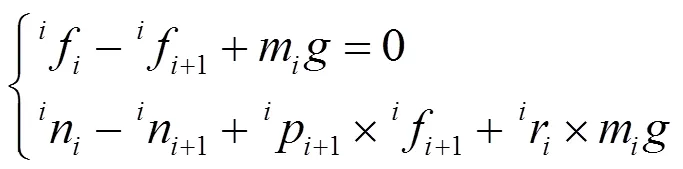
式中：矢量左上标为该矢量在坐标系{}中的表示；r为连杆的质心相对于{}的表示；p1为坐标系{＋1}原点相对于坐标系{}的表示。

忽略连杆自身的重力，式（4）写成反向迭代的形式，为：

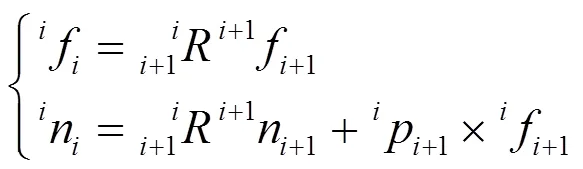
通过旋转矩阵将式（5）右端力（矩）表示在自身坐标系{＋1}中，在忽略连杆自重的情况下，根据力和力距平衡方程，从末端连杆开始逐次向基坐标反向递推，得到各连杆所受到的力和力矩。利用连杆变换矩阵[3]，将力和力矩写成在自身坐标系中的表示，计算每个关节驱动力和力矩，从而得到由操作力矩向各个关节力和力矩映射的雅克比在末端连杆坐标系的描述：

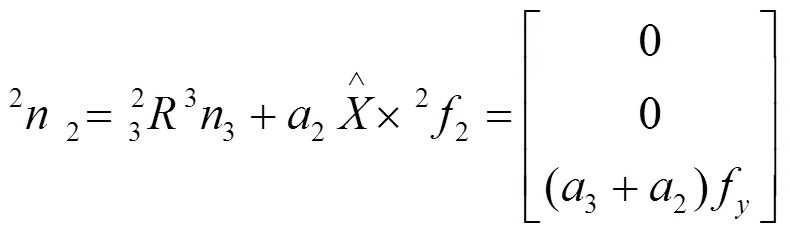
为了求出保持系统静平衡所需要的关节力矩，应计算关节轴矢量和施加在连杆上的力矩矢量的点积，于是有：

得力雅克比矩阵：

对所得计算结果进行分析验证，得出力雅克比矩阵是雅克比矩阵的转置。证明此机构建立的正确性，为今后的动力学分析奠定了基础。

2 基于ADAMS对机械手动力学仿真

2.1 SolidWorks运动学模型的建立

本文所分析的机构是在SolidWorks软件下进行实体建模，如图3所示。几何建模后，通过各种约束来限制构件间的自由度，以达到需要的相对运动，以此就把各构件连接成一个机械系统。

图3 机械手简化模型

2.2 机械手动力学分析

前面研究了机械手的静态位置、静态力和速度，但还未考虑引起运动所需的力。机械手是一个不断运动、受到各种力的动力系统，为多参数变量的非线性耦合系统[9]。机械手动力学主要研究的是机械手各个关节的运动与关节需要的驱动力之间的关系。

现今求解动力学问题的方法主要分为两大类：一是运用机械手运动参数，递推并建立牛顿－欧拉方程，另一类是利用机械系统、能量平衡，对机械手的变量参数进行微分，求得机械手各关节变量。

本文采用拉格朗日法建立动力学方程，为今后进行伺服电机和减速机的选型做理论基础准备。伺服电机的选型应该尽量较精确地符合运动模型，这样便于优化机电系统，有利于精确控制。

流程如图4所示，先求得机械臂的动能和势能，然后建立拉格朗日函数，最终对函数求导并得到动力学方程。

图4 拉格朗日动力学方程求解示意图

三自由度机械臂的动能、势能分别为：

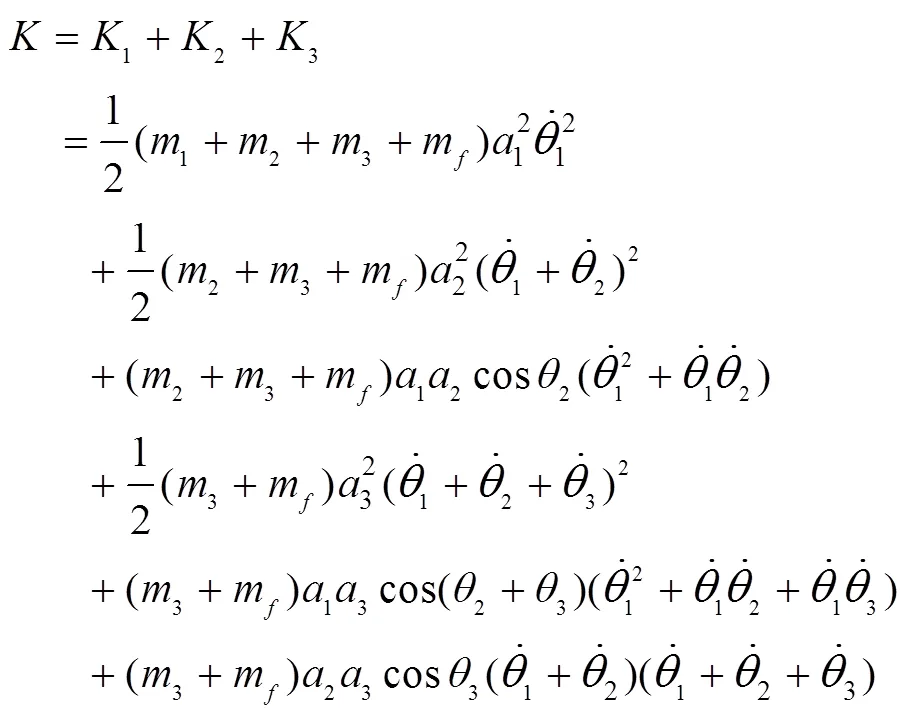
式中：1、2、3分别为杆1、2、3的动能；1、2、3分别为杆1、2、3的势能；m为负载质量。

拉格朗日动力学公式给出了一种从标量函数推导动力学方程的方法，这个标量函数为拉格朗日函数，即一个机械系统的动能和势能的差值：

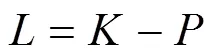
式中：和可以用任何方便的坐标来表示。

则机械手的动力学方程可表示为：

2.3 动力学仿真

在SolidWorks中完成建模后，注意保证各个零件的相对位置关系，减少在ADAMS中的更改。在SolidWorks插件中找到SolidWorks Motion勾选，进行运动算例1，选择Motion分析，选中模型右键“输出到ADAMS”[10]，最后在ADAMS环境中生成三自由度机械手的虚拟样机如图5所示。机械手各组件的连接如表2所示。

对机械手运动进行仿真、使用后处理模块，在各个关节处分别添加如下驱动函数：

STEP( time , 0 , 0d , 1 , -60d )

STEP( time , 0 , 0d , 1 , -60d )

STEP( time , 0 , 0d , 1 , 60d )

图5 虚拟样机

表2 机械手各组件的连接

绘制各个关节力矩、角度、角速度、角加速度随时间的变化曲线，如图6所示。

机械臂的旋转角度变化导致动力学各个参数发生变化，在一定时间内，转角越大、速度越快，每个关节所需驱动力矩也就越大。

3 结论

（1）采用D-H参数方法，建立了三自由度机械手运动学模型，并得到了机械手运动学正解。当已知关节角位移变量时，可以获得机械手末端相对于基座的位置。

（2）获得机械手的雅可比矩阵和力雅可比矩阵，并相互验证以获得正确的结果，为今后动力学分析奠定了基础。

（3）利用ADAMS软件对机械手添加运动约束驱动并进行仿真，得到各关节处力矩、角度、角速度、角加速度的关系曲线，为机械手控制的研究奠定了基础。

图6 各关节参数的变化曲线

[1]熊有伦，丁汉，刘恩沧. 机器人学[M]. 北京：机械工业出版社，1993.

[2]张立杰，李永泉，黄真. 球面二自由度5R并联机器人的运动学分析[J]. 中国机械工程，2006，17（4）：39-41.

[3]吴振彪，王正家. 工业机器人[M]. 2版. 武汉：华中科技大学出版社，2006.

[4]林义忠，吉慧丹. 六自由由度喷漆机器人动力学分析[J]. 机械设计与制造，2011（4）：141-143.

[5]焦恩璋，陈美宏. 6R串联机器人雅可比矩阵求解和速度仿真[J].机床与液压，2010（9）：110-113.

[6]石炜，郗安民，张玉宝. 基于凯恩方法的机器人动力学建模与仿真[J]. 微计算机信息，2008（29）：222-223，196.

[7]李庆龄，赵永生. 六自由度工业机器人动力学分析与仿真[J].上海电机学院学报，2008（4）：275-278.

[8]陈敏华. 机器人动力学模型新方法[J]. 机床与液压，2003（1）：134-137.

[9]张兆龙，孙金风，胡亮. 丝杆移动型爬杆机器人的机构设计与分析[J]. 机械，2018，45（1）：66-71.

[10]魏晓霞，蒲小琼，冯常. 基于水下爬行机器人的机械手结构设计[J]. 机械，2015，42（4）：77-80.

[11]董伯麟，彭航. 工业机器人逆运动学的奇异回避算法[J]. 机械设计与研究，2016（2）：35-40.

[12]刘海涛，杨乐平，朱彦伟，等. 空间机器人工作空间研究[J]. 组合机床与自动化加工技术，2011（8）：26-29.

The Establishment and Dynamics Simulation of Three-Degree-of-Freedom Manipulator Jacobian Matrix

CAI Yuqiang，ZHANG Wenrui

( School of Mechanical Engineering, North China University of Science and Technology, Tangshan 063210, China )

Through the simulation technology based on ADAMS, this paper analyzes the kinematics and dynamics simulation of industrial machinery. For the three-degree-of-freedom industrial pick-up robot, the reference coordinate system of each link is established by the DH method. First, the main theory and mathematical foundation of the robot are studied, and the kinematics equations of the robot are obtained. The posture relationship between the connecting rod and the end effector is derived, the kinematic equation of the robot is developed, and the Jacobian matrix is obtained by the differential change method. Through the recursion of the force and moment between the connecting rods, deli Jacobian matrix is obtained to verify the correctness of the robot establishment. Then the manipulator motion was simulated in ADAMS using the post-processing module. The driving function was added to each joint respectively, and the feasibility of the mechanism was verified.

manipulator；three-degree-of-freedom；Jacobian matrix；ADAMS

TH113

A

10.3969/j.issn.1006-0316.2020.12.009

1006－0316 (2020) 12－0061－07

2020－07－14

河北省教育厅项目（2019GJJG216）；华北理工大学博士启动基金项目（BS2017094）

蔡玉强（1967－），男，河北唐山人，博士，教授，主要研究方向为机械机构学与机械动力学，E-mail：caiyq@ncst.edu.cn。