相干态表象下的两类不对称积分投影算符

侯丽丽，王 帅

(江苏理工学院 数理学院，江苏 常州 213001)

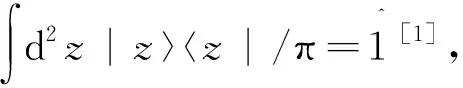
(1)

(2)

又会得到什么物理结果哪？显然，式(2)所表示的不对称积分投影算符的构造方式与式(1)大不相同。那么，这样的投影算符是幺正算符还是厄米算符呢?如果是厄米算符，它是否有着经典对应呢?在本文的工作中，将利用IWOP积分技术研究以上两个问题。

1 双模转动算符的相干态表象表示

在量子力学中，IWOP积分技术在量子算符的运算以及幺正变换过程中是非常有用的一种积分工具。下面，本文首先利用IWOP积分技术导出式(1)所示的不对称积分投影算符的显式。为了便于对不对称积分投影算符的理解，本文将给出详细地推导过程。

(3)

(4)

该式中符号::的左边都是产生算符，右边都是湮灭算符，积分算符本身就是算符的正规排序形式。因此，式(4)中符号::两侧的算符可以放置到::内，即

(5)

这样就可以利用IWOP积分技术对式(5)进行积分，给出积分算符的显式。注意到以下积分公式

(6)

其积分收敛条件Re(ζ)<0，对式(5)直接积分可得

(7)

为了把算符的正规乘积排序符号::去掉，借助算符恒等式

(8)

最终，不对称积分投影算符式(1)有如下的简单形式，即

(9)

该不对称积分投影算符恰好就是量子相空间中的双模转动算符，它是一个幺正算符[12]。

2 宇称测量算符的相干态表象表示

接下来，利用IWOP积分技术计算式(2)不对称积分投影算符的显式，并讨论它的物理意义，这是本文的主要工作。与推导式(9)相类似，首先把式(2)积分投影算符改写成正规乘积形式下的积分，即

(10)

这样就可以利用IWOP积分技术直接对式(10)进行积分了。再次利用积分公式(6)，可得式(10)的积分显式为

(11)

与式(9)不同，容易证明下式中左右两端积分投影算符相等，即

(12)

所以，式(2)(或式(11))不对称积分投影算符是一个厄米算符。既然它是一个厄米算符，在量子力学中也许有其经典物理对应，即对应某个物理量或某种物理测量。特别地，当φ=0时，式(11)就简化为文献[13]中的结果，即

(13)

同时，文献[13]证明了式(13)对应的是在马赫-曾德尔(MZI)干涉仪中的宇称测量，具体来讲就是参数化后的双模量子态光场经过最后一个分束器后的宇称测量(光子数的奇偶测量)。下面按照同样的思路，我们推广文献[13]的研究结果，解析地证明式(2)(或式(11))代表的是双模量子态光场经过更为一般分束器后的宇称测量方案。

图1 基于马赫-曾德尔干涉仪的量子精密测量方案示意图，虚线框为宇称测量部分

如图1所示，MZI干涉仪是一个具有两个输入端口和两个输出端口的光学仪器，在量子精密测量中有着重要且广泛的应用[14-17]。虚线框前的部分为光场量子态经过第一块分束器BS1后，再经过相位产生器(phase shifter)，这一过程通常称为参数化过程。参数化后的量子态用|Ψ〉ab表示。这里相位产生器描述光经过干涉仪的两条光路所产生的相位差φ。在真实的实验中，它可以用于模拟诸如引力波或者存在某种介质等因素所引起的两条光路的相位改变，这正是需要测量的相位。在MZI干涉仪输出端光场的量子态下，计算宇称算符的期望值称为宇称测量。方便起见，本文考虑的宇称测量方案包括MZI干涉仪最后一块分束器BS2在内，如图1中虚线框所示。此时，宇称测量可以表示为

(14)

(15)

并存在如下幺正变换关系

(16)

(17)

(18)

该式右边算符的正规排序好了。因此，利用IWOP技术对该式右边积分可得，

(19)

当θ=π/2时，即考虑平衡分束器时，上式简化为

(20)

比较式(11)和式(20)，最终可得

(21)

可见，如式(2)所示的厄米算符确实有其经典物理对应，即双模量子态经过更为一般分束器后的宇称测量，式(21)就是本文最重要的一个研究结果。

(22)

(23)

(24)

3 结论