基于Erlang分布蓄水容量曲线的流域产流模型

闫宝伟,李正坤,段美壮,江慧宁,刘 昱

(1. 华中科技大学土木与水利工程学院,湖北武汉 430074；2. 中国电建集团华东勘测设计研究院有限公司,浙江杭州 311122)

根据蓄满产流原理,降水首先补充土壤缺水量,在流域土壤达到田间持水量以后,流域产流。蓄水容量曲线用于描述流域土壤缺水量空间分布不均匀的问题,曲线的形状决定着流域产流面积和产流量的多少,对于径流的准确模拟具有重要意义。流域蓄水容量受流域下垫面地形和土壤等多种因素影响,通常难以直接测量,蓄水容量的空间分布更难以确定,通常是经验假定。在新安江模型中广泛采用B次抛物线表示蓄水容量曲线,至于为何采用该类线型,至今尚无合理解释。为能反映雨季和枯季蓄水容量曲线的灵活性,周买春和Jayawardena[1]提出了双抛物线型蓄水容量曲线,以反映不同土壤水分并存状态下的蓄水容量。流域蓄水容量曲线同时也是对流域地形地貌特征的一种反映,Gao等[2]通过对美国404个流域的洪水模拟发现,流域地形地貌对抛物线型蓄水容量曲线的参数B有较大影响。TOPMODEL中的地形指数同样反映了流域的缺水情况,其累计频率曲线与蓄水容量曲线实质是一致的,都是对流域缺水量空间不均匀性的一种描述,郭方等[3]提出了利用TOPMODEL地形指数的分布推求流域蓄水容量曲线的思路。石朋等[4]通过对流域内栅格地形指数的统计分析,采用对数韦布尔分布曲线描述流域蓄水容量空间分布的不均匀。孔凡哲和宋晓猛[5]根据各子流域的平均坡度计算蓄水容量的空间分布。向小华等[6]则进一步提出了融合土壤和地形的栅格蓄水容量计算方法,为研究流域蓄水容量的空间分布提供了一种有效工具。Wang[7]针对SCS模型中的土湿比函数没有考虑土壤蓄水容量空间分布不均匀性的问题,提出了一种新的分布函数来描述土壤蓄水容量的空间分布。Gao等[8]根据植被根系深度随距离最近河道高程的空间分布规律,建立了以地形为基础的土壤含水量和变源产流面积间的非线性关系,提出了一种新的产流模型,为无资料地区的水文模拟提供了一种可行的工具。

本文尝试通过栅格蓄水容量的计算,分析多个典型流域蓄水容量的空间分布型式,选用Erlang分布曲线进行流域产流的推导,提出基于Erlang分布蓄水容量曲线的流域产流模型,一方面可以更加真实地反映流域的产流过程,另一方面,也为无资料地区的产流计算提供一种可行途径。

1 流域蓄水容量的空间分布

流域蓄水容量的实质是流域下垫面的缺水量,与流域的地形地貌有较大关系,对流域的产流有直接影响,由于蓄水容量难以直接测定,其空间分布更是难以直接确定。考虑到新安江模型中的蓄水容量与TOPMODEL 中缺水量的概念相对应,而TOPMODEL可以根据地形指数和流域平均缺水量计算出各点的缺水量,进而可以分析流域缺水量或蓄水容量的空间分布。蓄水容量除了与流域地形有关之外,还受到土壤类型的影响,如黏性土壤的土壤颗粒间孔隙较小,相应的土壤缺水量也较小；而砂质土壤的土壤颗粒间孔隙较大,相应的土壤缺水量也较大。向小华等[6]以van Genuchten模型表述的土壤水分特征曲线为基础,推导出了融合地形和土壤特征的流域栅格单元蓄水容量的计算公式:

(1)

式中:Wi为某点的蓄水容量,mm；Di=Szm[max(tpi)-tpi],为某点的地下水埋深,mm；Szm为流域内非饱和区的最大蓄水深,mm；tpi为地形指数；θr、θf和θs分别为土壤凋萎含水量、田间持水量和饱和含水量；ψc为土壤水分达到田间持水量时毛管上升高度,mm；β、m为土壤水参数。各种土壤水分特征参数的取值见文献[9],Szm则由流域平均蓄水容量试算而得,流域平均蓄水容量可通过参数率定得出,无资料地区可采用Gao等[10]和Wang-Erlandsson等[11]提出的MCT方法进行估算。

按式(1)计算表1所示典型流域的栅格蓄水容量,得到各典型流域蓄水容量的空间分布,如图1所示。

表1 所选典型流域属性表

图1 典型流域蓄水容量的空间分布Fig.1 Spatial distribution of watershed storage capacity in the selected basins

2 流域蓄水容量曲线线型分析

Erlang分布是一种连续型概率分布,该分布与指数分布一样多用来表示独立随机事件发生的时间间隔,常应用于保险业以及排队论中[12]。Erlang分布作为伽马分布的特例,计算和应用较为便捷,且对该分布函数的积分易得出显式表达式,可以简化后续的产流计算,由此选用Erlang分布作为新的蓄水容量曲线线型,其概率密度函数为

(2)

式中:Γ(·)表示伽马函数；n、λ为参数;n值为整数。若式中参数n取值为实数,则式(2)即为伽马分布的密度函数。Erlang分布是一种伽马分布,表示独立随机事件发生的时间间隔,水文中广泛应用的Nash瞬时单位线就是伽马分布函数。对上式积分可得其分布函数:

(3)

式中:En(x)为Erlang分布函数。

根据流域蓄水容量的空间分布,进一步统计蓄水容量不同量级所占的面积比例,绘制流域蓄水容量的面积分布图,并采用正态分布、对数正态分布、指数分布、Erlang分布等多种不同型式的分布函数以及常用的抛物线型曲线进行拟合,发现Erlang分布拟合效果更优,如图2所示,图中α表示产流面积比。

图2 典型流域蓄水容量分布的拟合图Fig.2 Fitness of distribution of the storage capacity in the selected basins

3 基于Erlang分布蓄水容量曲线的产流计算

参考抛物线型蓄水容量曲线定义,则基于Erlang分布的蓄水容量曲线可以表示为

(4)

式中:W′为流域中某点的蓄水容量；Wmm为流域中最大的点蓄水容量。

采用Erlang分布蓄水容量曲线计算流域产流,如图3所示,则由蓄满产流原理可知,流域平均蓄水容量

(5)

上式的推导用到了Erlang分布的如下性质[13]:

(6)

同理可得流域初始蓄水容量

(7)

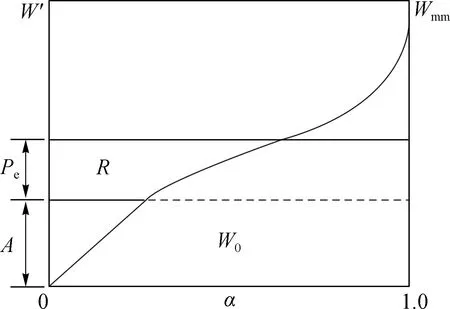
图3 流域蓄水容量分布曲线与降雨径流关系Fig.3 Watershed storage capacity distribution curve and its rainfall runoff relationship

式中:A为初始蓄水容量W0对应的纵坐标。为计算产流量,需首先确定A的值,在已知W0的情况下,A可以通过求解式(7)而得,而该式为A的隐式方程,很难直接求解,此处采用牛顿迭代法进行求解。令

(8)

进一步对上式求导可得

(9)

根据牛顿迭代公式可知,经过i次迭代后,得

(10)

当相邻两次迭代值之差小于允许误差时,便可求得A的数值解。根据蓄满产流原理,有效降雨Pe产生的径流为

(11)

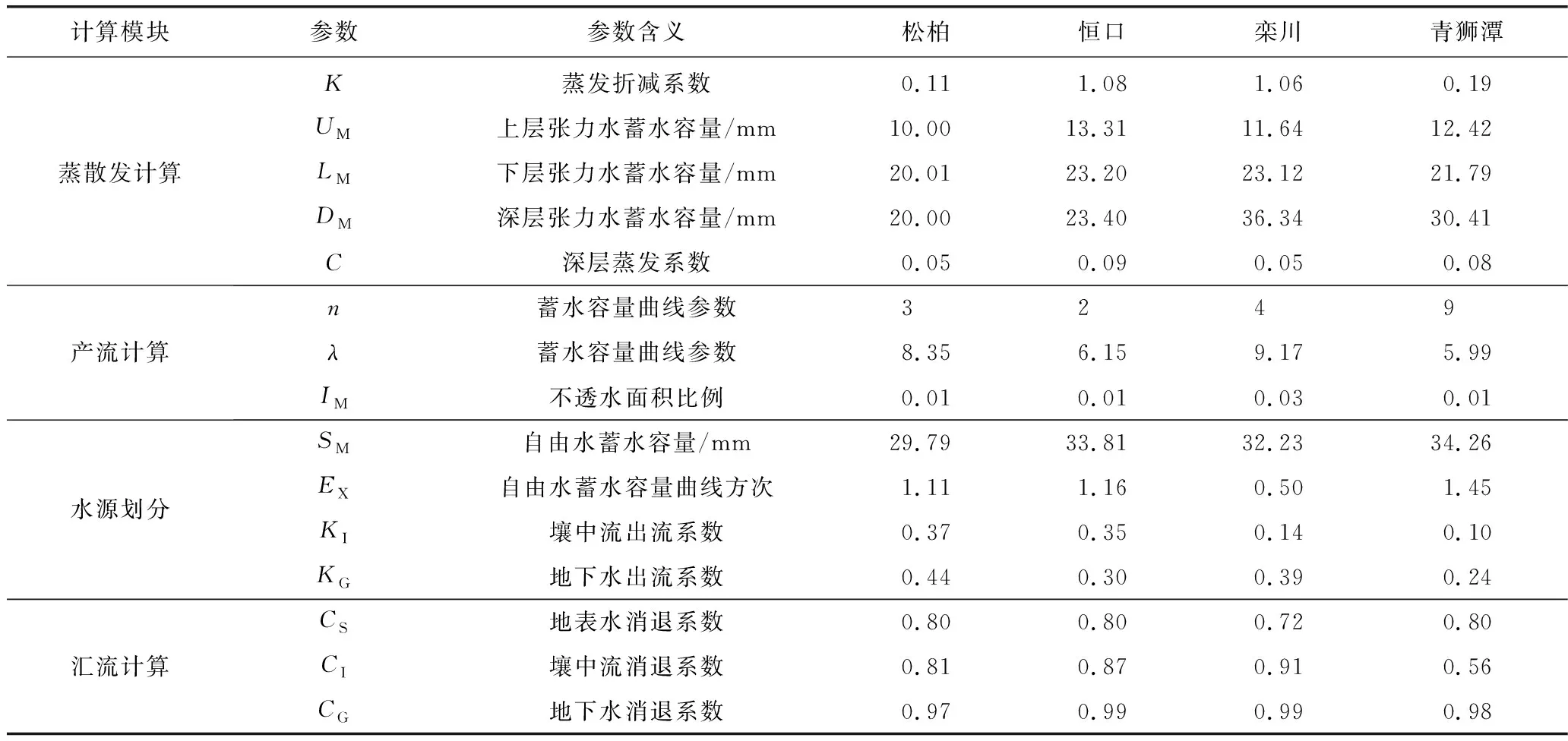
综上,若Pe+A

(12)

若Pe+A≥Wmm,即全流域产流时:

R=Pe-Wm+W0

(13)

在产流计算中,只要给定流域平均蓄水容量Wm和Erlang分布的参数n、λ,即可实现产流计算。在无资料地区,也可根据式(1)计算出的栅格蓄水容量,统计出流域蓄水容量的分布曲线,采用极大似然估计等参数估计方法估算Erlang分布的参数,从而可以实现无资料地区的产流计算。在资料丰富的地区,可以根据降雨径流资料直接进行参数率定。

4 模型应用

将新安江模型的产流模块替换成上述基于Erlang分布蓄水容量曲线的流域产流模型,汇流模块仍然采用原算法,其中,壤中流和地下径流汇流采用线性水库法,河网汇流采用滞后演算法,由此得到改进的新安江模型。将改进后的模型分别应用于松柏、恒口、栾川和青狮潭4个典型流域的洪水模拟,以分析模型的应用效果。

选取松柏流域1983—2012年、恒口流域1980—2017年、栾川流域1998—2010年和青狮潭流域2002—2015年的场次洪水用于模型的率定和检验。其中,模型的参数采用SCE-UA算法进行优化率定,计算时段长均为1 h,模型参数模拟结果如表2所示。

表2 模型参数模拟结果

选取洪峰相对误差、峰现时间误差和洪水总量相对误差以及确定性系数作为模型精度评价指标,分别计算每场洪水的评价指标值,表3给出了各个流域这些评价指标的平均值以及与新安江模型的结果对比。可以看出,松柏流域和恒口流域的模拟精度与新安江模型相当,栾川流域和青狮潭流域的模拟精度有一定提高,尤其是栾川流域的提高较为明显,率定期确定性系数由0.73提高到0.80,其他指标也都有不同程度的提高。图4进一步展示了栾川流域检验期3场洪水的模拟结果,可以发现,改进后的模型无论是洪峰还是洪水过程的模拟都取得了较高的精度,相比新安江模型也都有提高。

表3 洪水模拟结果平均值统计及对比

图4 栾川流域检验期洪水过程模拟结果Fig.4Simulated flood hydrographs in the validation period in Luanchuan station

5 结 论

蓄水容量曲线的形状决定着流域产流面积和产流量的多少,对于径流的模拟有直接影响。通过对多个典型流域蓄水容量空间分布的分析,选用Erlang分布曲线进行流域蓄水容量曲线的拟合,提出了基于Erlang分布蓄水容量曲线的流域产流模型,主要结论如下:

(1)基于Erlang分布推导了一种新的流域产流模型,相比新安江模型增加了1个产流参数,模型的适应性增强,模拟结果更接近实际的产流过程,一定程度上提高了模型的模拟精度。由于增加了模型参数,可能会增加其他参数如Wm的不确定性,需进一步分析。

(2)基于Erlang分布蓄水容量曲线产流模型的参数,可以借助流域的地形和土壤类型数据进行估算,为无资料地区的产流计算提供了一种可行的途径。