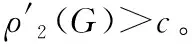不含5-圈平面图的边存活率
郭文婷,孔将旭
(中国计量大学 理学院,浙江 杭州 310018)
1995年,Hartnell[1]首次提出了消防员问题(Firefighter Problem)。设G是一个连通图,k是正整数。假设火在图G的一个顶点或多个点燃起,消防员每步选择k个没有着火的顶点加以防护,然后火蔓延到其未被保护且没有着火的邻点,火和消防员在图G上交替移动。当火没法再传播时,整个过程结束。
为了研究一个图的整体防火能力,蔡雷震和王维凡[2]首先提出了图的存活率的概念。设G是n阶连通图,snk(v)表示当v为火源点时,k个消防员最多能防护的顶点个数。当火等概率的在图G的一个顶点燃起时,k个消防员最多能保护的顶点数的期望称为图G的k-存活率,记为ρk(G),即
显然,0<ρk(G)<1,且对任意i>j,有ρi(G)≥ρj(G)成立。关于存活率和消防员问题的最新研究进展,请参阅王维凡和孔将旭的综述文献[3]。
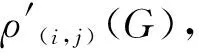
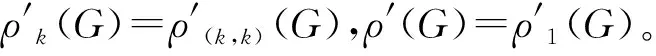

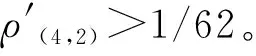
1 几个预备引理设
G是简单平面图,我们用V(G),E(G),F(G),Δ(G)和δ(G)分别表示图G的顶点集、边集、面集,最大度和最小度。对v∈V(G),N(v)={u|uv∈E(G)},点v的度数d(v)=|N(v)|。对f∈F(G),用b(f)表示围成面f的周界,d(f)表示围成面f的周界的边数,称为f的度。一个度为k,至少为k或至多为k的点(面)分别称为k-点,k+-点或k--点(k-面,k+-面或k--面)。对于一条边uv,如果u是i-点,v是j-点,那么uv边称为(i,j)-边,并且用f1和f2表示与uv相关联的两个面,当uv是割边时,f1=f2。对于一个3-面[uvw],如果u是i-点,v是j-点,w是k-点,那么[uvw]面称为(i,j,k)-面。
引理1[8](平面图分离定理)设G是一个极大平面图,|V(G)|=n,T是G的任意一棵支撑树,则存在一条边e∈E(G)E(T)使得T+e中的唯一一个圈C满足圈内和圈外的点数都小于(2n)/3。
引理2[6]设G是平面图,T是G的任意一棵以r为根点的支撑树,则T中存在一条以x,y为端点的路P(xy),使得圈C=P(xy)+{xy}(xy可以不是G中的边,x,y≠r)满足圈内和圈外的点数都小于(2n)/3。


由引理4我们可以得到以下推论。
推论1设G是n(≥24)阶不含5-圈平面图,uv∈E(G)。如果d(u)+d(v)≤9,那么sn(4,2)(uv)≥(n-4)/3。
令E1(G)={uv∈E(G)|d(u)+d(v)≤9}。
推论2设G是n(≥24)阶不含5-圈平面图,uv∈E(G),并且uv仅关联一个3-面。如果d(u)+d(v)≤10,那么sn(4,2)(uv)≥(n-4)/3。
令E2(G)={uv∈E(G)|uv仅关联一个3-面且d(u)+d(v)≤10}。
推论3设G是n(≥24)阶不含5-圈平面图,uv∈E(G),并且uv关联两个3-面。如果d(u)+d(v)≤11,那么sn(4,2)(uv)≥(n-4)/3。
令E3(G)={uv∈E(G)|uv关联两个3-面且d(u)+d(v)≤11},E*(G)=E1(G)∪E2(G)∪E3(G)。
2 (4,2)-边存活率
本节我们运用权转移的方法证明最小度至少为3且不含5-圈的平面图的(4,2)-边存活率大于某个正常数。
对任意的uv∈E(G),首先我们对每条边定义初始权函数
其中a=1/42。由欧拉公式|V(G)|-|E(G)|+|F(G)|=2,可导出下面的等式:
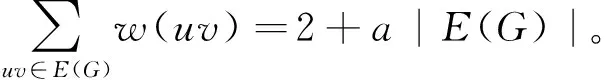
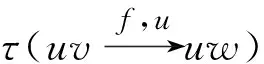
(Rule)设uv∈E(G)E*(G)关联两个3-面f1=[uvw]和f2=[uvz],d(u)=i,d(v)≥12-i,其中3≤i≤6。假设d(w)≤d(z)。(如图1)
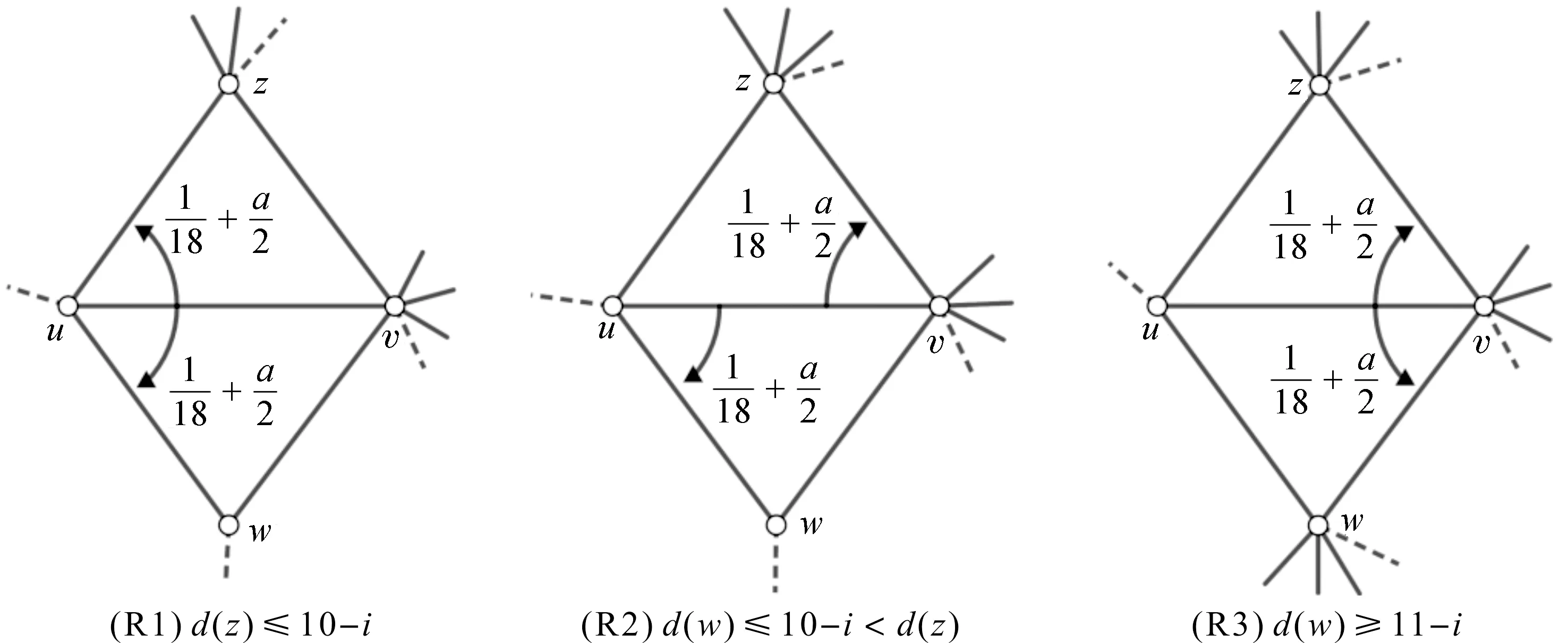
图1 权转移规则示意图Figure 1 Discharging rules
(R1)若d(z)≤10-i,则
(R2)若d(w)≤10-i (R3)若d(w)≥11-i,则 因为G是最小度至少为3的不含5-圈平面图,所以G不含下面三个结构: (i)5-面; (ii)两个相邻的3-面和4-面; (iii)3-面相邻两个不相邻的3-面。 观察1设xy∈E*(G),则xy最多得到权1/9+a。 断言1设xy∈E(G)E*(G)。若xy为(9+,9+)-边,则xy最多得到权1/9+a,此时xy关联一个(3,9+,9+)-面;否则,xy最多得到权1/18+a/2,特别地,如果xy是(3,8+)-边,则xy得不到权。 证明设xy关联的两个面为f1和f2,由对称性,不妨设d(f2)≥d(f1)。 1)d(f2)≥d(f1)≥4,则根据(Rule)xy不得到权。 2)d(f2)≥4,d(f1)=3,设f1=[xyz]。只有当fxz和fyz都是3-面,边xz和yz才给边xy各转权1/18+a/2,即2×(1/18+a/2)=1/9+a。由于G不含3-面相邻两个不相邻的3-面,所以fxz和fyz相邻,此时d(z)=3,由(Rule)得d(x)≥9,d(y)≥9,即f1是(3,9+,9+)-面。如果xy是(3,8+)-边,那么只有当xz关联两个3-面时才转权,此时d(z)≥9,根据(R2)得xy没得到权。 3)d(f1)=d(f2)=3,设f1=[xyz],f2=[xyw]。由于G不含3-面相邻两个不相邻的3-面,当d(y)≥d(x)≥4时,fxz,fyz,fxw,fyw都是4+-面,因此xy得不到权;当d(x)=3时,因为xy∈E(G)E*(G),由推论3得d(y)≥9,若fxz,fyz,fxw,fyw都是4+-面,则xy得不到权,否则其中至少有一个是3-面,由于G不含3-面相邻两个不相邻的3-面,因此zw∈E(G)且fxz=fxw,由(Rule)得只有当z和w都是9+-点时才转权,并且由(R3)得xy没得到权。因此,断言1得证。 引理5设G是不含5-圈的连通平面图,n>23,δ(G)≥3,则对G的每条边uv满足: 1)若uv∈E*(G),则w0(uv)≤4/9+2a; 2)若uv∈E(G)E*(G),则w0(uv)≤0。 证明1)若uv∈E*(G),当d(u)=d(v)=d(f1)=d(f2)=3时,初始权最大。由观察1得,边uv最多得到权1/9+a。因此, 2)uv∈E(G)E*(G),设f1和f2是与uv关联的两个面(当uv是割边时,f1和f2是同一个面),且d(f1)≤d(f2)。根据推论1得d(u)+d(v)≥10。 ①d(f1)≥4。由(R1)—(R3)得,边uv既没有得到权也没有转出权。因此, w0(uv)=w(uv) ②d(f1)=3,d(f2)≥4。由推论2得,d(u)+d(v)≥11,不妨设d(u)≤d(v)。因为G不含5-面,两个相邻的3-面和4-面以及3-面相邻两个不相邻的3-面,所以d(f2)≥6。由于uv只关联一个3-面,因此uv至多得到权2×(1/18+a/2)。 若d(u)≥6,则 若d(u)=5,则d(v)≥6,由断言1得uv最多得到权1/18+a/2,从而得 若d(u)=4,则d(v)≥7,由断言1得uv最多得到权1/18+a/2,从而得 若d(u)=3,则d(v)≥8,由断言1得uv没得到权,从而得 ③d(f1)=d(f2)=3。由推论3可得,d(u)+d(v)≥12。由(R1)—(R3)得,边uv通过关联3-面f1,f2转出权2×(1/18+a/2)。因此, 证明由于经过权转移后权和保持不变,可得下面的不等式, 因此, 由于图F是有2n+2个点和5n条边且最小度为3的平面图(如图2),不难证明ρ′(F)→0(n→∞),所以至少需要两个消防员。因此,对最小度至少为3的平面图的边存活率我们提出如下问题。 图2 图FFigure 2 Graph F DOI:10.11845/sxjz.2020007a. DOI:10.11845/sxjz.2020007a.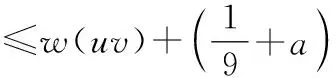
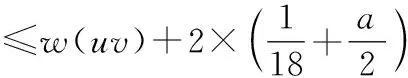
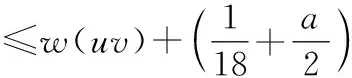
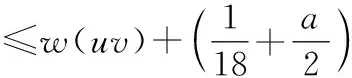
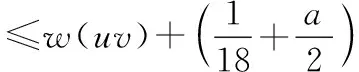

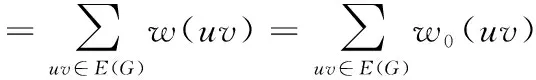
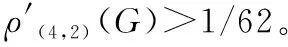
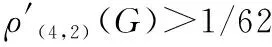
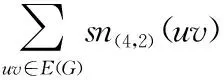
3 结 语