基于工人-工序关联学习率的批量加工周期研究

谷梦瑶,侯鹏飞,戴之希

(1.中国计量大学 质量与安全工程学院,浙江 杭州 310018;2.华电漯河发电有限公司 生产技术部,河南 漯河 462000)

随着客户需求越来越多样化、小批量化,对于批量生产而言,首先,其加工周期的准确界定直接影响着订单和生产计划的制定;其次,是否能快速完成订单以满足客户需求、缩短批量产品的制造周期,成为企业是否能增强竞争力的关键[1]。缩短产品制造周期的一个重要途径在于实现生产合理化,缩短零件的加工周期。在生产过程中,一种零件往往包含若干数量,零件的生产通常是成批进行的[2]。因此,研究批量零件加工周期的相关问题具有十分重要的现实意义。一般情况下,计算批量零件的生产周期时主要考虑工件批量、工件的移动方式和工艺等[3],忽视了工人的因素。同时,关于批量零件加工周期优化问题的研究较多,如:

1)通过零件移动方式的选择,提高零件在生产过程中的连续性,以缩短加工周期[4];

2)通过对调度算法的研究解决批量调度问题,从而优化加工周期[5-7];

3)在批量生产过程中尽量采用通用夹具和刀具,或设计专用刀、夹具,并尽量让工序集中,减少装夹次数和磨刀、换刀时间,减少或消除对工件的校正等,从而提高零件的生产效率[8];

4)通过优化批量生产中的工艺路线或工艺压缩时间以减少加工时间[9]。

以上研究大多是从批量生产中的客观事物来考虑的,也是研究最多的方向,鲜有考虑工人本身所具有的学习特征,及将将工人学习率与批量零件加工周期相结合的研究。本文的创新点即来源于此。

1936年,Wright研究了飞机生产中单件工时随产量而下降的规律,第一次建立了学习曲线[10]。随后,关于学习率的研究越来越多,学习曲线被广泛应用于制造、服务和管理等领域的多个方面[11-13]。已有研究结果表明:人工作业时间所占比例越大,学习率就越低,学习系数就越大;反之,学习率越高,学习系数就越小[14],即手工程度越高的工序,受工人学习率的影响越大。人工作业系统是众多中小型企业,特别是产品装配阶段的主要组织形式[15],可见研究人工作业系统不失一般性和实际意义。因此,为更好地研究工人学习率对批量零件加工周期的影响,本文选择人工作业系统为研究对象。在人工作业系统中考虑学习率的研究较少,已有研究中又以不同工人的学习率相同为前提来研究批量加工模式的优化[16],或者以不同工人学习率不同,但在各个工序工艺上保持不变为前提[17]等。本文的不同之处在于:将不同工人的学习率视为不同,且在各个工序工艺上动态变化,即在不同工序上考虑关联学习率。

综上所述,本文在人工作业系统中考虑工人-工序关联学习率,研究批量零件加工周期的计算和优化问题,具有创新性和实际意义。

1 关联学习率和作业组织模式

1.1 学习曲线

随着累计产量的增加,操作者生产制造的熟练程度提高,产品单台(件)工时消耗呈下降趋势,由此形成工时递减的函数曲线称为学习曲线。学习曲线通常有狭义和广义两种解释。狭义的学习曲线是指操作人员的个人学习曲线,随着时间的推移,知识和经验得到有效的积累,它反映了个人操作技术熟练程度的提高。本文采用狭义学习曲线。学习曲线呈指数函数关系,可由莱特公式(1)表示:

Y=KX-α;

(1)

(2)

式(1)(2)中,Y为生产第X台(件)产品的工时,K为生产第1台(件)产品的工时,α为学习系数,C为工时递减率或学习率。学习率的范围在50%～100%之间[14]。工人学习率越大,其学习速度越慢。本文假设工人自身拥有固定的学习率。

1.2 工人-工序的关联学习率

同一工人在不同工序上表现的学习率不同,工序操作难度越大,工人对此工序的学习效果越差,学习率的值越大。因此需要用工序的操作难度来修正工人自身的固定学习率,以修正后的学习率表示工人在该工序上的准确学习率,修正后的学习率即为工人-工序的关联学习率。由于工人自身学习率固定,关联学习率与工序操作难度成正相关,工人i加工工序j时,关联学习率计算公式可表示如下:

Cij=Fj·Ci。

(3)

式(3)中:Cij为工人i与工序j的关联学习率;Fj为工序j的操作难度,其值可根据表1中的工序操作难度评价指标体系,利用三角模糊语言变量[18]和层次分析法得到;Ci为工人自身的固定学习率。

表1 工序操作难度的评价指标体系

1.3 人工作业系统中的作业组织模式

人工作业系统运作模式是按客户订单组织生产,客户订单为多品种、中小批量。人工作业系统的作业组织模式主要包括小组作业模式和生产线作业模式。小组作业模式即整组工人同时执行相同工序,完成上道工序后再同时执行下道工序;生产线作业模式即把小组工人分配到各工序,组成一条生产线。其中,小组作业模式中零件的移动方式为顺序移动,生产线作业模式中零件移动方式包括平行移动和平行顺序移动两种[16]。本文仅分析生产线作业模式-零件平行移动的情况,另外两种情况的分析类似,不赘述。

2 批量零件加工周期

批量零件的生产周期是指从批量原材料或零部件投入生产开始,以某种移动方式让批量零件经过各道工序(含工艺工序和运输工序)加工或搬运直至成为成品出产为止,所经历的全部日历时间。某批量为n的零件,每个零件需经过m道工序完成,其中j表示第j道工序;完成这批零件加工的小组中共有p个工人,p≥m,其中i表示工人i,每道工序只由1个工人完成,将有m个工人被一对一分配到各道工序上,剩余工人将做辅助工作。为使研究问题更加明确,对模型做如下假设:1)批量零件按生产线作业模式进行加工,零件平行移动;2)工序顺序固定,各道工序的初始加工时间、操作复杂度已知;3)工人都是多技能工,能胜任各道工序;4)各个工人的学习率已知,且工人之间的学习率有差异,同一工人在不同工序上的学习率有差异;5)批量零件按订单生产,订单相似度不大,不考虑工人在各工序上的初始经验程度。

2.1 不考虑关联学习率的批量加工周期

批量零件按生产线模式加工,零件平行移动,m个工人被一对一分配到各道工序上,不考虑工人的学习率,加工周期计算公式如下:

(4)

式(4)中,tj表示第j道工序的初始加工时间;第k道工序的初始加工时间最长,tk=max{tj|j=1,2,…,m}。工序的参数固定时,加工周期为定值,加工周期与工人无关。

2.2 考虑关联学习率的批量加工周期

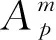
2.2.1 加工周期的计算

在某一工人分配方案中,工人1～m被分配至m道工序上,此时批量零件加工周期计算公式如下:

(5)

式(5)中:Cij为工人i与工序j的关联学习率,可用式(3)求得;第k道工序的初始加工时间最长;当k=1时,式(5)中无第一项,当k=m时,式(5)中无第三项。

参考式(5),进一步可得所有工人分配方案的加工周期计算公式如下:

(6)

其中,

当k=1时,式(6)中第一项无;当k=m时,式(6)中第三项无。

2.2.2 加工周期优化模型

(7)

(8)

另外,在一定条件下,此加工周期优化模型可简化。式(7)中与初始加工时间最长的瓶颈工序k相关的时间为

(9)

Tl占总时间T的比率为

(10)

当比率v足够大,并在容许范围内时,可将优化模型进行简化,简化模型如下:

(11)

(12)

其中,V为规定的Tl占总时间T的最小比率,即当v≥V时原模型才能被简化。

简化后,组合优化问题变成单个优化问题,即只需安排第k道工序的工人使得Tl最小,减少其他工序的变动以降低变动带来的成本。

3 数值算例和分析

为简化计算,更直观分析内在规律,假定:工序的操作难度为1;小组工人数与工序数相等均为4个;第一道工序的工时最长即k=1;零件加工批量为1 000。其加工工序和工人学习率的相关数据如表2。

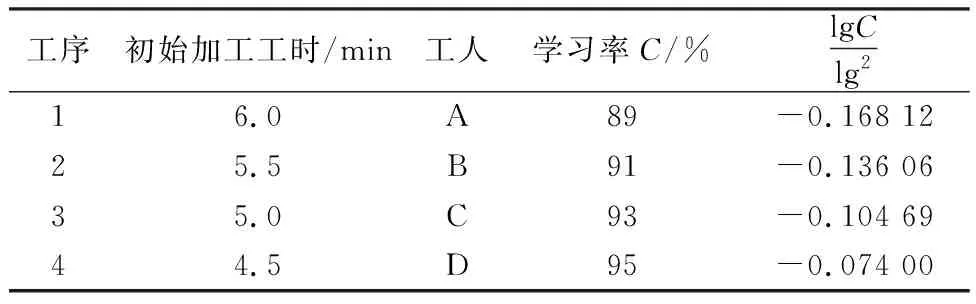
表2 零件与工人的相关数据Table 2 Related data of parts and workers

3.1 加工周期的计算优化

批量加工周期优化模型中的目标函数为

(13)

1)当工人的安排顺序为ABCD时,加工周期计算如下:

5×1 000-0.104 69+4.5×1 000-0.074 0=

2 262.12 min。

(14)

2)当工人的安排顺序为DCBA时,加工周期计算如下:

5×1 000-0.136 06+4.5×1 000-0.168 12=

3 890.72 min。

(15)

按同样的方法一一计算得24种工人安排方案对应的加工时间如表3。

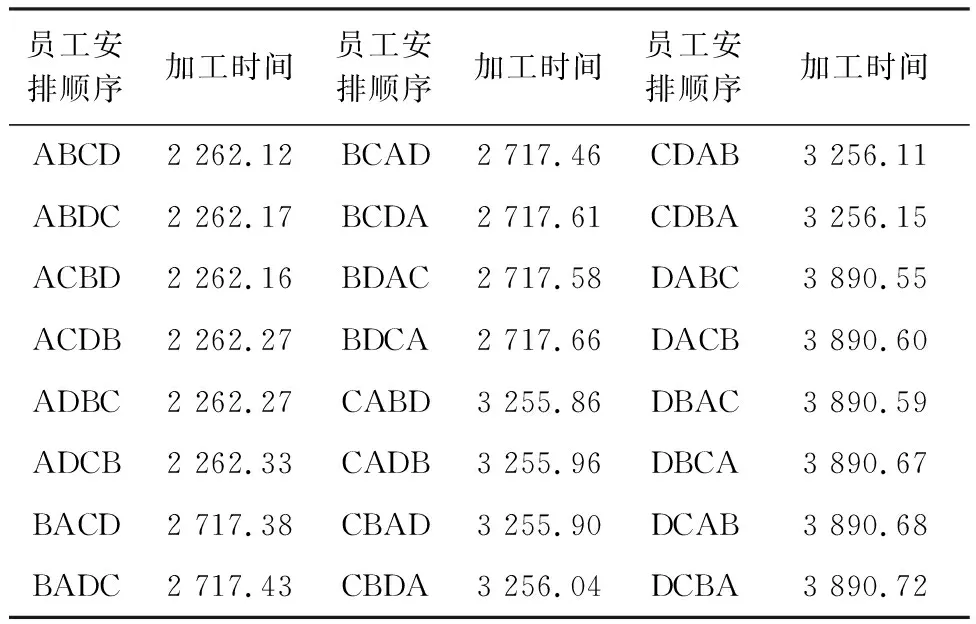
表3 工人安排对应时间穷举表

通过分析表中数据,可知:1)工人的最佳安排顺序是ABCD,此时有最优的批量加工周期即2 262.12 min;2)工人的最佳安排顺序是DCBA,此时有最差的批量加工周期即3 890.72 min;3)第一道工序即瓶颈工序的工人不变时,其余三道工序的人员变动对加工周期的影响很小;4)第一道工序即瓶颈工序的工人变化,对加工周期的影响很大;5)通过计算可得,在不同的工人排序中,第一道工序的相关时间占总时间的比率v均在99.7%左右;6)若容许模型简化的最小比率V为95%,则能够简化模型中的目标函数,形成类似式(11)的目标函数;7)简化后的最佳方案是只需保证工人A加工第一道工序即可,其他工人可维持原来的位置以减少变动。

3.2 零件批量对周期优化的影响

当最长工序所占比率v足够大,在误差容许范围内可简化批量零件周期优化模型。为解答在何种情况下比率v能足够大,与批量大小是否存在关系的问题,可分析比率v与批量n的影响关系;本文选择在最佳安排ABCD中分析,其他参数不变,比率v随批量n的变化函数为:

(16)

利用MATLAB软件绘制出其函数曲线如图1,图中横坐标表示批量n,纵坐标表示比率v。由图可知,比率与批量正相关,当批量为150时,比率已超过98%。故当批量较小时,不仅要考虑最长工序的工人选择,其他工序也需对应选择,即批量周期优化模型不能简化;若最佳周期时间可接受2%的变化,当批量超过150时,只需选择在最长工序上学习率最小的工人即可,其余员工可尽量维持优化前的匹配以减少变动,即批量周期优化模型可以简化。

图1 比率与批量的函数曲线Figure 1 Function curve of ratio and batch size

3.3 不同批量下加工周期对学习率的敏感性分析

通过计算可知在最佳安排ABCD中,若工人A的学习率降为86%即学习效果变好,批量零件加工周期将减少25%。工人学习率的变化对加工周期有影响,当零件批量不同,学习率的变化对加工周期的影响大小是否不同。为此,做如下验证。

通过图1可得:当批量大于50时,Tl的比率超过90%,由于Tl接近于T,且Tl受学习率的影响显然大于其他项,故可用Tl在不同批量下受学习率变化的影响代表T在不同批量下受学习率变化的影响。同样,选择最佳工人排序进行分析,在100、500、2 000三个批量下,工人学习率递减时,加工周期下降率vt随学习率C的变化函数。

当n=100时,加工周期下降率计算公式如下:

(17)

绘制函数曲线,三个批量下加工周期下降率与学习率的关系曲线如图2。横坐标为学习率,取其在90%～75%中递减;纵坐标为加工周期下降率vt。三条曲线从上到下分别是批量为2 000、批量为500和批量为100时,加工周期下降率随学习率变化的关系曲线。

图2 加工周期下降率与学习率的函数曲线Figure 2 Function curve of decline rate and learning rate of machining cycle

结果分析:1)批量越大,批量零件加工周期对工人学习率的变化越敏感;2)批量越大,降低工人学习率带来的效果越好,即加工周期下降率越大。

4 结 论

本文对人工作业系统中考虑工人-工序关联学习率的批量零件加工周期相关问题进行了研究,选择生产线线作业-零件平行移动模式为对象,得出了在考虑学习率后批量零件加工周期的计算公式和优化模型,并提出在一定情况下的简化模型。同时,通过算例分析得到批量对模型能否简化存在影响,以及在不同批量下,学习率的变化对加工周期的影响程度不同。本文的研究思路新颖,具有一定的理论和实际应用价值。同时,本文也存在一些需进一步研究的问题,如选择有效的算法对加工周期优化模型进行求解和在计算加工周期时考虑工人的遗忘率等,有待后续研究。