桥墩轴线初始偏位缺陷对桥墩承载能力影响研究

韩 绪

(中交第一公路勘察设计研究院有限公司，陕西 西安 710065)

0 引 言

随着国民经济水平的提高，为实现交通路网四通八达，高速公路网加密及国省干道改扩建的重心逐渐向山区发展。受山区地形、地貌影响，高墩、大跨桥梁逐渐增多。对于山区预制结构桥梁，高墩常采用矩形空心墩。同时由于桥墩是桥梁的主要承重结构，直接承受上部结构传下的荷载，桥墩施工垂直度直接影响桥梁运营安全。但在施工过程中由于实际施工处理不当等原因出现施工偏差，导致桥墩轴线偏位，至使桥梁结构实际受力状态与设计受力状态不吻合，从原轴心受压状态变为偏心受压，桥墩承载能力受到影响，甚至会出现严重偏离的情况，直接影响桥梁结构的运营安全。

1 工程概况

本文以某高速公路两跨40 m简支T梁桥为依托，上部结构采用5片预制T梁，T梁腹板中心距为2.3 m，梁高2.5 m；下部结构桥墩采用等截面双肢矩形空心墩，截面尺寸为3 m×2.5 m，墩高30 m，双墩中心间距为8 m，盖梁采用T型盖梁，盖梁顶部宽为3 m，底部宽为1.8 m，高为2.3 m，桥墩基础采用桩基础。

2 计算荷载取值

2.1 恒载取值

根据工程数量表计算得到单片主梁所需混凝土约为43 m3，混凝土容重25 KN/m3，单片主梁恒载为1 075 KN。

2.2 活载取值

本桥采用的设计荷载为公路-Ⅰ级，计算梁端支反力横向分布系数采用杠杆法(偏安全考虑，未计入多车道折减系数)，3车道正载横向分布系数计算图如图1所示；计算3车道正载工况下5个支座的支座反力，荷载布置图如图2所示。

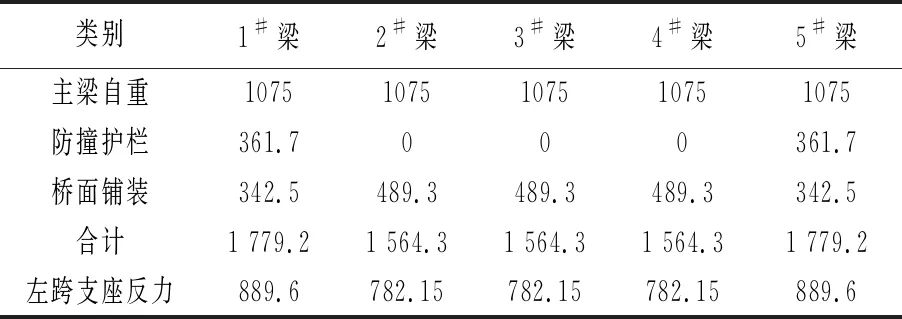
表1 墩顶盖梁恒载支座反力KN

图1 3车道正载横向分布系数计算图

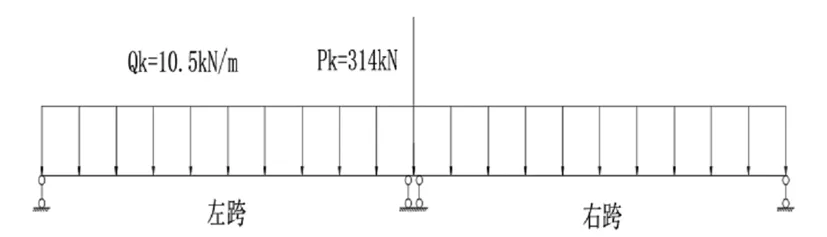
图2 纵桥向活载布置图

其中：η1=η5=0.5×0.6=0.3

η2=η4=0.5×(0.4+0.88+0.36)=0.82

η3=0.5×(0.12+0.64+0.64+0.12)=0.76

考虑横向分布系数后5个支座的反力分别为：337.67 KN、312.96 KN、123.54 KN、337.67 KN。

3 有限元模型建立

3.1 计算软件的选择

目前结构静力分析相关的有限元软件较多，其中Midas FEA为实体单元分析软件，具有多样化的建模方式，以及强大的分析功能；Midas Civil为一款建模高效的杆系单元分析。Midas Civil假定截面变形后仍保持平面，而在Midas FEA实体单元中，不再使用平截面假定，截面变形后的形状通过截面上任意一点的应变来反应；这使得实体单元分析相对于杆系单元分析能够更加精确模拟桥墩轴线初始缺陷，得到更为精确的计算结果，因此本文主要采用Midas FEA进行建模。

3.2 不同偏位工况模拟

桥墩承受的荷载包含桥梁上部结构的自重、桥墩自重以及桥梁正常情况下的汽车活动荷载；模拟过程中支座支反力作为外荷载，盖梁及桥墩自重荷载在有限元模型中考虑。本文针对双柱空心墩分2个工况建立了有限元模型，总共9个计算模型，具体如下。

工况一：最大偏位出现在左墩距墩底20 m截面处，不同偏移量，共5种工况，有限元模型如图3所示。

模型1：最大偏位为15 cm；模型2：最大偏位为25 cm；模型3：最大偏位为35 cm；模型4：最大偏位为45 cm；模型5：最大偏位为55 cm；

工况二：最大偏位为15 cm时，不同高度，共4种情况，有限元模型如图4所示。

模型6：距承台高26 m处最大偏位为15 cm；模型7：距承台高20 m处最大偏位为15 cm；模型8：距承台高16 m处最大偏位为15 cm；模型9：距承台高12 m处最大偏位为15 cm。

图3 工况一有限元模型 图4 工况二有限元模型

4 桥墩关键截面承载能力计算

4.1 关键截面选取

结合实际情况，选取如图5所示5个关键截面进行承载能力验算，Z1～Z5截面分别为左侧桥墩距承台顶面26 m、22 m、20 m、16 m、12 m，Y1～Y5截面分别右侧桥墩距承台顶面26 m、22 m、20 m、16 m、12 m，截面廓尺寸为顺桥向宽3 m，横桥向宽2.5 m，壁厚0.4 m。

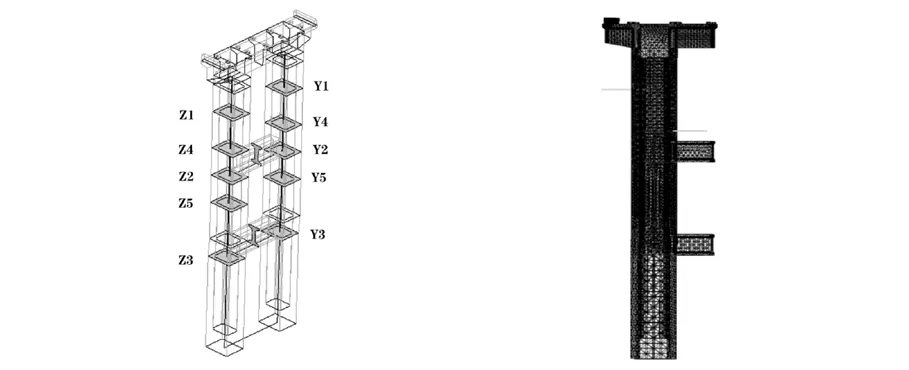
图5 关键截面选取 图6 有限元模型网格划分

4.2 关键截面内力计算

通过限元软件Midas FEA分析计算，从计算结果中提取关键截面Z1～Z5、Y1～Y5在两组数值模型中的竖向轴力Fx、绕y轴弯矩My，桥墩最大轴线偏位在20 m高处不同偏位情况下各关键截面内力提取结果、最大偏位量15 cm不同高度情况下关键截面内力汇总分别如表2、表3所示，表中Fx以压力为正。x轴以竖直向上为正，y轴以内侧向外侧方向为正，表中效应值已考虑荷载组合系数与结构重要系数。

4.3 关键截面承载力计算

根据《公路圬工桥涵设计规范》(JTG D61-2005)中第4.0.8条与第4.0.9条规定，混凝土双向偏心受压承载能力计算图示如图7；各截面偏心距e均小于允许的限值0.6 s，受压构件偏心距计算图如图8所示。

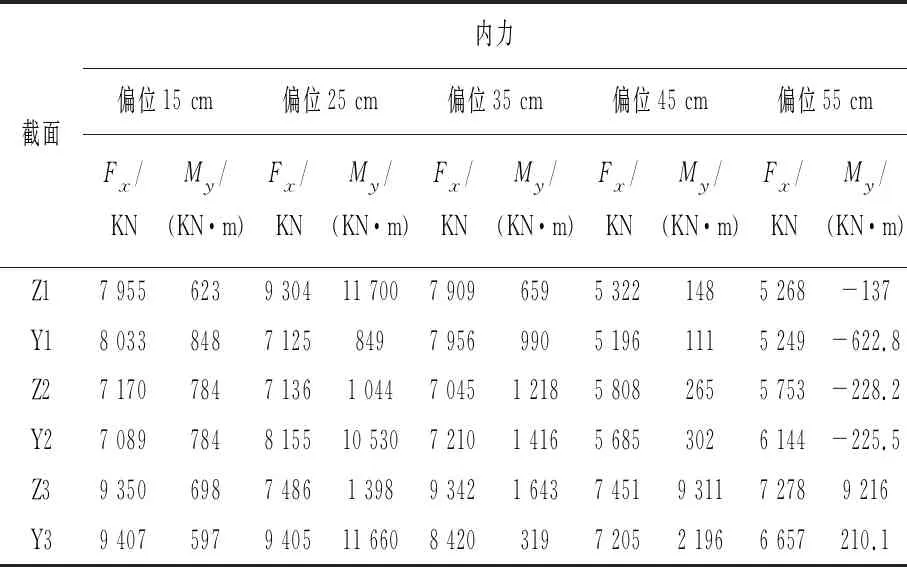
表2 工况一：最大偏位在20 m处，不同偏位关键截面内力汇总

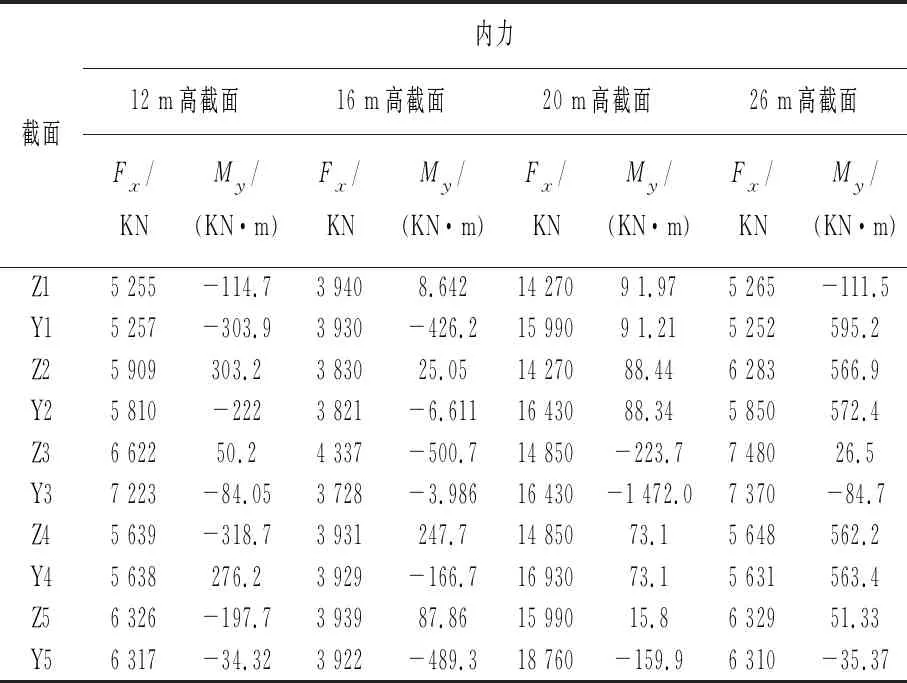
表3 工况二：最大偏位量为15 cm，不同高度关键截面内力汇总

图7 双向偏心受压承载能力计算图

图8 受压构件偏心距计算图示

双向偏心受压构件承载能力计算：受压区高度和宽度按额才ecy=ey，ecx=ex确定；矩形截面偏心受压承载力按γ0Nd≤ψfcd[(h-2ey)(b-2ex)]计算；轴心受压构件弯曲系数查表取ψ=0.82，fcd=22.4 MPa，桥墩轴线最大偏位在距左墩墩底20 m高处时，偏位为15 cm、25 cm、35 cm、45 cm、55 cm状态下各截面承载能力计算结果如表4所示；最大偏位量为15 cm，不同高度26 m、20 m、16 m、10 m处关键截面承载能力计算结果如表4所示。根据表4作出工况一、二各自五种情况的曲线对比图。

(1)最大偏位在距左墩墩底20 m处时，不同最大偏位量所对应的承载能力，用于分析偏移量对承载能力的影响趋势，如图9所示。

(2)最大偏位量均为15 cm时，12 m、16 m、20 m、26 m四个不同高度处各关键截面所对应的承载能力，用于分析偏移在桥墩竖直方向上对承载能力的影响，如图10所示。

图9 不同偏位量关键截面承载力对比图

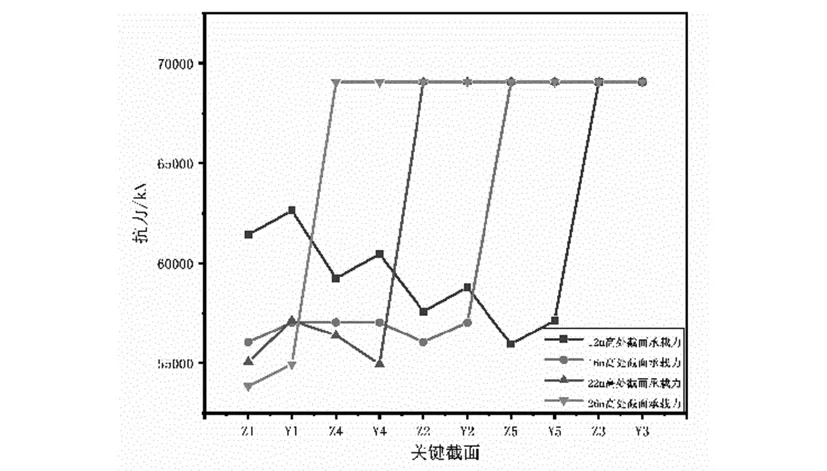
图10 不同高度关键截面承载力对比图

表4 工况一、二关键截面承载能力计算结果

5 分析与结论

根据图9可知，桥墩轴线偏位从15 cm变化到25 cm其承载力下降1/10，25～35 cm承载力下降1/5，35～45 cm承载力下降1/4，45～55 cm承载力下降1/3；根据计算结果可发现，同一截面偏位量越大，桥墩承载能力越小，且增大相同幅度偏位，桥墩承载能力下降速度有明显增加趋势。

根据图10可知，距墩底高12 m处发生15 cm偏位时，桥墩的承载力相对于距墩底高16 m处发生15 cm偏位时的承载力提高了1/50～1/10；距墩底高16 m处发生15 cm偏位时，桥墩的承载力相对于距墩底高22 m处发生15 cm偏位时的承载力提高1/100～1/50；距墩底高22 m处发生15 cm偏位时，桥墩的承载力相对于距墩底高26 m处发生15 cm偏位时的承载力提高了1/100～1/50；从计算结果可发现，不同高度桥墩轴线发生相同的偏位，随着最大偏位截面所处位置的提高，桥墩承载能力逐步下降。

因此，对于山区高墩桥梁，在桥墩施工过程中应加强桥墩垂直度监测，尽量避免桥墩偏位情况发生，若发现桥墩偏位应及时进行纠偏处理，不能任其发展，墩高越高，偏位越大时桥墩承载能力越低。