基于ADAMS 的轴承内圈内径形位公差检测装置研究
刘武发,李 攀,王福荣
(郑州大学机械工程学院,河南 郑州 450000)
1 引言
智能化生产线是智能化制造的关键,轴承作为机械中重要的支撑零件,对轴承进行智能化生产线工序间检测是一种关键技术。其中轴承内圈内径如圆度、垂直度和壁厚等参数是轴承重要的形位精度指标,决定着轴承的旋转精度、装配精度和定位精度等,是轴承使用寿命和使用性能的重要评估指标。目前国内、外对轴承的检测发展了新的检测方法和检测仪器。文献[1]针对轮毂轴承内圈端面平行度误差测量进行研究,采用了误差补偿的测量方法;文献[2]提出了基于轴承内圈沟道新的方法对轴承内圈的旋转精度进行研究;文献[3]提出了基于TRIZ 的方法来对航空发动机轴承内径进行测量,采用了夹紧装置和标准量块组合的方法,使测量的结果具有了更高的测量精度。但是,国、内外对轴承的测量大多是单一测量,缺乏对轴承的综合测量的方法和装置,并且大多都运用理论和实验研究的方法,一方面耗费时间,另一方面耗费成本。因此基于虚拟样机技术和ADAMS 动力学仿真软件来研究轴承内圈形位公差的综合检测装置变得尤为必要,可以大大简化产品的开发周期,通过无数次物理样机无法进行的仿真实验,来获得最优的设计方案[4-6]。
因此基于虚拟样机技术和ADAMS 动力学仿真技术重点研究轴承内圈形位公差的综合检测装置。
2 检测装置的结构和特点
轴承内圈内径检测装置主要由驱动部分和定位部分等组成,驱动部分由滚轮4、7 构成;定位部分主要由支点2、支点5、支点8 和支点9,构成测量轴承内圈内径参数如直径、圆度、垂直度和壁厚等检测的定位支点。检测装置的原理图,如图1 所示。该装置采用支撑轴承下端面的平台作为检测基准。当检测轴承内圈内径的圆度时,采用三点定位的方法。支点5、支点2 和传感器10 一起对轴承的内径进行定心,滚轮4 的旋转驱动轴承旋转,轴承旋转的过程中传感器采集数据,经过一定的算法计算出圆度误差;当检测轴承内圈内孔对端面的垂直度时,支点5 和支点2 互成90°对轴承内圈进行定心,滚轮4 的旋转驱动轴承旋转,在支点2垂直的上方的传感器1 对轴承进行测量,测量基准是轴承的下端面,在轴承的旋转过程中,传感器1 测量的最大值和最小值之差即为内孔对端面的垂直度;当测量轴承内圈外沟道的壁厚时,支点8 和支点9 互90°对轴承内圈进行定心,滚轮7 的旋转驱动轴承旋转,传感器6 正对支点8,传感6 测的最大值与最小值之差即为轴承内圈沟道壁厚误差。此检测装置能够按照设定的顺序自动地测量轴承内圈上述参数误差,检测速度快,精度高;提供给轴承内圈旋转动力的滚轮的运动状态,对轴承参数检测的影响很大,此外还有轴承运转过程中轴承下端面的跳动量和轴承运转的平稳性对轴承各检测参数的影响,为此,重点研究滚轮的运动状态和轴承下端面的跳动量对轴承检测装置的误差测量的影响。
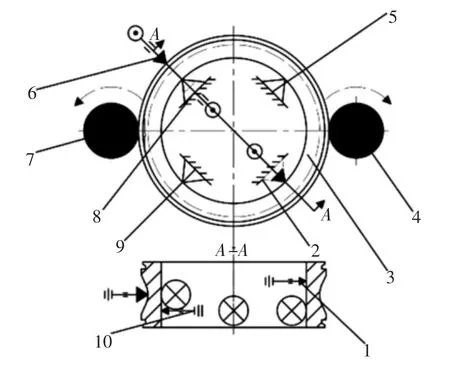
图1 检测装置原理图Fig.1 Schematic Diagram of Detection Device
3 影响测量精度的因素及误差分析
3.1 轴承内圈内径圆度检测的误差分析
在测量轴承内圈内径的圆度误差时,一方面采用三点定位的测量原理,因此支点与测点的对应关系对测量的精度很重要,另一方面采用统一的测量基准-工作台,因此工作台的平面度也对测量基准有一定的影响。
3.1.1 支点与传感器连线没有通过轴承内圈圆心的误差分析
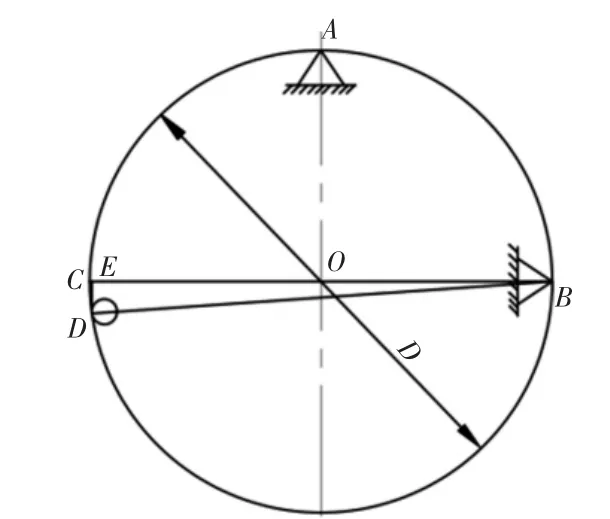
图2 径向定位误差分析Fig.2 Analysis of Radial Positioning Error
图中:BC—理论直径;BD—实测直径;A、B—固定支点;DE—偏移距离;D—理论直径。
测量轴承内圈内径的圆度,理论上要求支点与测点连线通过轴承内圈的圆心,实际因各种安装和加工因素等原因,引起支点与测点的连线偏离轴承内圈的圆心,此时的测量误差为ε1,误差分析,如图2 所示。

式中:DE—偏移距离;∠DBE—实测点与支点的连线与理论测点与支点连线的夹角;BD—实测直径;BC—直径;ε1—测量误差。
分析式(1)可知,测点偏移的距离DE 越小,那么轴承内圈内径的圆度测量误差越小,因此在调整轴承内圈检测仪时,要注意测点与支点连线通过中轴承内圈圆心的准确度,使偏移距离尽量小。
3.1.2 工作台的平面度对轴承内圈圆度测量的误差分析
测量轴承内圈的圆度误差,一方面要考虑支点与测量点的安装因素等引起的测量误差,另一方面既要考虑测量的基准问题引起的测量误差,因轴承内圈检测装置采用基准统一的原则,基准的因素对测量误差是影响很大的,因此工作台的平面度对圆度测量误差的影响是不容忽略的,由此引起的测量误差为ε2,误差分析,如图3 所示。
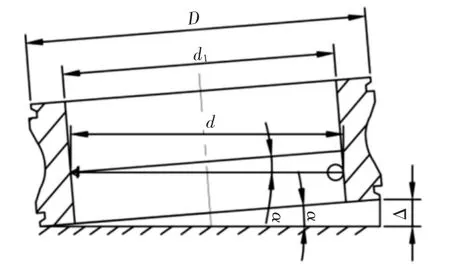
图3 垂直方向的误差分析Fig.3 Vertical Error Analysis
图中:Δ—工作台的平面度;α—工作台与水平面的倾角;d—实测的内径;d1—轴承的理论直径;D—轴承的内外径,测量误差。

式中:Δ—工作台的平面度;D—轴承的内外径;d1—理论直径;d—实际直径;ε2—测量误差。
分析式(2)可知,工作台的平面度Δ 越小,轴承内圈内径圆度测量误差越小,同时此检测装置对轴承内圈的内外径的尺寸是有一定要求的,轴承内外径的尺寸不能太小,因此在测量轴承内径圆度误差时,要兼顾这两个方面因素。
3.2 轴承内圈沟道壁厚检测的误差分析
3.2.1 支点与测点的连线没有通过沟道的最低点的误差分析
测量轴承内圈沟道的壁厚,理论上要求支点与测点的连线通过轴承内圈沟道的最低点,实际上因加工和安装原因等引起支点与测点连线没有通过轴承沟道的最低点,导致沟道壁厚测量产生误差,此时的测量误差为σ1,误差分析,如图4 所示。

图4 壁厚径向误差分析Fig.4 Radial Error Analysis of Wall Thickness
图中:C 点—实际测点;B 点—理论测点;O 点—沟道圆弧的圆心;A 点—理论测点C 在OB 上的投影点;AC—测点理论点的距离。

式中:CD—实测沟道半径;OC—理论半径;OB—理论沟道半径;OA—实测点在理论测量方向上的投影长度;AC—测点与理论点的垂直距离。
分析式(3)可知,测点偏移理论测点的距离越小,那么沟道壁厚的测量误差就越小,因此在调整轴承内圈沟道壁厚的检测装置时,要尽量是实际测点与支点的连线通过轴承内圈沟道的最低点。
3.2.2 工作台的平面度对轴承内圈沟道壁厚测量的误差分析
同轴承内圈内径圆度的检测一样,沟道壁厚的测量基准也是工作台的平面,因此工作台的平面度同样对轴承内圈道壁厚的测量产生一定的测量误差,此时的测量误差为σ2,误差分析,如图5 所示。

图5 壁厚垂直方向的误差分析Fig.5 Error Analysis in the Vertical Direction of Wall Thickness
图中:AC—理论沟道壁厚;BC—实测沟道壁厚;DE—轴承的内圈外径;EF—工作台的平面度,用Δ 表示,工作台与水平面的倾角为α。

式中:Δ—工作台的平面度;DE—轴承内圈外径;AC—理论壁厚;BC—实测壁厚。
分析式(4)可知,工作台的平面度Δ 越小,轴承沟道壁厚测量的误差就越小,同时轴承的内外径的大小对测量误差也有一定的影响,轴承内外径的尺寸越大,沟道壁厚的测量误差就越小,即在调整轴承沟道壁厚的测量装置时,要注意工作台的平面度和轴承内外径的大小。
3.3 轴承内圈内径垂直度检测的误差分析
测量轴承内圈内径垂直度时,要求支点和测点的连线通过轴承内圈内表面的母线,实际上因各种安装因素和加工因素等原因,导致测点与支点的连线没有通过轴承内圈内表面的母线,而是偏离了一定角度θ,如图6 所示;此时的测量误差为γ,误差分析,如图7 所示。

图6 测点倾斜图分析Fig.6 Inclination Map Analysis of Measurement Points
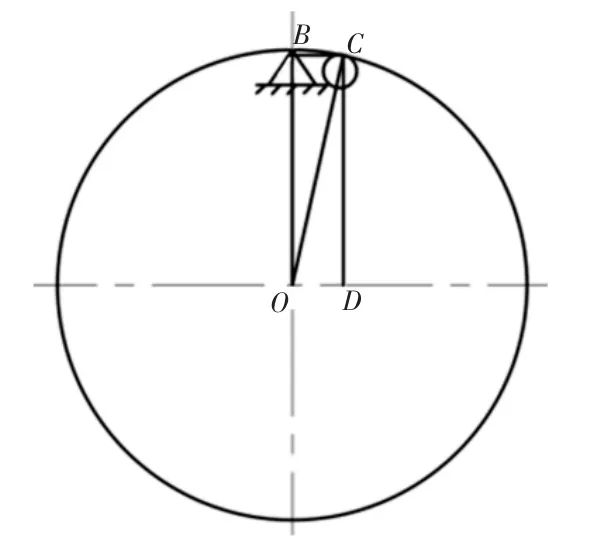
图7 垂直度的误差分析Fig.7 Error Analysis of Perpendicularity
图6 中:AC—支撑测点的导杆偏移距离;EC—导杆的长度,暂且设EC=L,图7 中实际上测量垂直度就是测量轴承内圈表面母线上一点相对于OD 所在平面并且垂直于轴承端面的平面的距离,OB 表示理论距离,CD 表示实测距离,此时的测量误差γ=OB-CD。
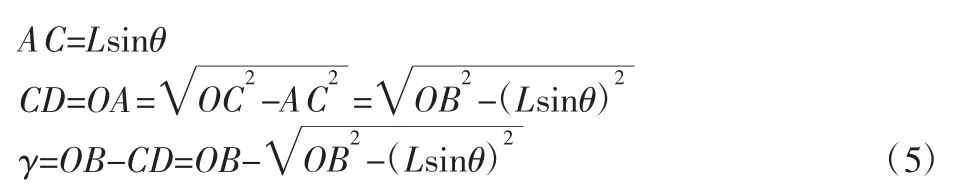
式中:AC—导杆偏移距离;L—导杆长度;θ—偏移的角度;CD—实测点的距离;OB—理论测点的距离;γ—测量误差。
分析式(5)可知,支撑测点导杆的偏移角度θ 越大,轴承内圈内径垂直度的测量误差就越大,同时支撑测点的导杆的长度不能越长,不然也会带来一定程度的测量误差,因此在调整轴承内圈内径垂直度检测的装置时,要尽量保证支撑测点导杆的偏移角度和导杆的长度。以上轴承内圈各参数检测的误差分析,主要从支点与测点的一致性和测量基准工作台的平面度两个方面出发,误差分析的结果可为轴承内圈参数检测装置的动力学分析和实验装置的测量提供分析依据和测量依据。
4 检测装置的仿真与数据处理
4.1 检测装置模型的建立
利用Solidworks 三维建模软件建立轴承内圈各参数测量的检测装置,并对轴承内圈每个参数测量的各自装置分别进行简化,再以parasolid 格式导出,此格式可以在Solidworks 和ADAMS之间提供精确的几何参数(如密度、转动惯量等),在保证检测装置的运动学和动力学特性的基础上,设置仿真的工作环境和模型物理量单位,并添加检测装置必要的约束、驱动和接触力。
4.2 轴承内圈内径圆度与垂直度测量装置的仿真与数据处理
测量轴承内圈内径圆度和垂直度时,测量装置不同之处是传感器的位置不同;在ADAMS 中对轴承内圈内径圆度和垂直度测量装置添加约束、接触和驱动后,对其影响测量误差的电机转速和气缸压强因素进行动力学分析,并且对轴承下端面的跳动量的进行测量,如图8 所示。并对其数据进行处理,分别得出轴承下端面跳动量的极差值与电机转速和气缸压强大小的关系图,如图9、图10 所示。

图8 轴承下端面的跳动量Fig.8 The Runout of the Lower End of the Bearing
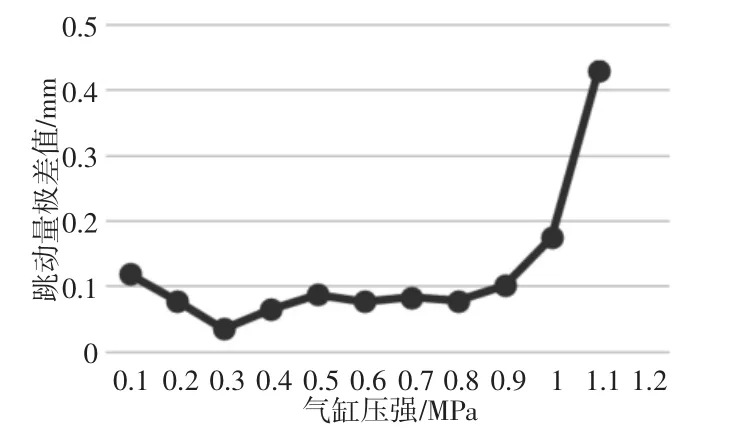
图9 轴承下端面跳动量极差值随气缸压强变化图Fig.9 Variation of Terminal Runout of Bearing with Cylinder Pressure

图10 轴承下端面跳动量极差值随电机转速变化图Fig.10 Variation of End Surface Runout of Bearing with Motor Speed
从图8 可以看出,轴承下端面跳动量在仿真过程中的变化呈现出近似正弦规律,为此我们取正弦图像的波峰和波谷的差值作为轴承下端面跳动量变化的极差值;从图9 可以看出,轴承下端面跳动量的极差值随着推动电机向前运动的气缸力呈现出一定的变化趋势,在气缸力刚开始比较小的时候,轴承下端面跳动量极差值有逐渐减小的趋势,随后极差值随气缸力的增大逐渐变大,因为实验条件得限制,气缸压强增加到0.5MPa 以后比较吃力,因此又做了一定的预测,发现气缸力再增大,极差值会变得非常大;从图10 可以看出,轴承下端面极差值随电机转速的变化比较平稳,并且发现实验最好的条件是电机转速为1r/s。
4.3 轴承内圈沟道壁厚测量装置的仿真与数据处理
对有关检测轴承内圈沟道壁厚的装置部分进行简化,并将其导入到ADAMS 进行动力学分析,为了评估测量误差因素对轴承沟道壁厚测量的影响,为此分别对气缸压强大小和电机转速大小对测量影响进行了分析,并对测量数据进行处理,分别绘制轴承下端面跳动量极差值随气缸压强和电机转速变化的数据图,如图11、图12 所示。
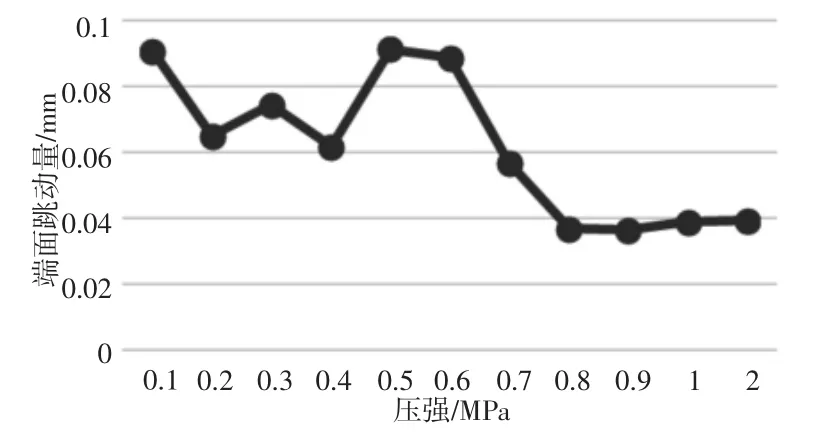
图11 轴承下端面跳动量极差值随气缸压强变化图Fig.11 Variation of Terminal Runout of Bearing with Cylinder Pressure

图12 轴承下端面跳动量极差值随电机转速变化图Fig.12 Variation of End Surface Runout of Bearing with Motor Speed
从图11 可以看出,在轴承沟道壁厚测量的动力学分析中,轴承下端面跳动量极差值随气缸压强的增加在大致趋势上逐渐减小;考虑到实验条件的限制,在气缸压强比较小的时候,0.2MPa作为实验条件的压强比较合适,再增加气缸压强的大小轴承下端面跳动量极差值会变小;从图12 可以看出,轴承下端面跳动量极差值的大小随电机转速增加,大致上有逐渐减小的趋势;
以上对轴承内圈有关形位公差检测(圆度、垂直度和壁厚等)的测量装置进行了ADAMS 动力学分析,分析了测量误差因素气缸压强大小和电机转速大小对形位公差检测的影响,动力学分析的结果可以为实验装置的分析提供理论依据。
5 实验验证
5.1 轴承内圈内径圆度和垂直度测量的数据验证
在与ADAMS 中仿真同样的条件下,为了验证仿真的正确性和合理性,搭建实验装置,并对轴承内圈内径圆度和垂直度参数进行测量,圆度测量的数据,如表1、表2 所示。垂直度测量的数据,如表3、表4 所示。
分析表1 可知,随着气缸压强的增大,轴承内圈的圆度误差值有逐渐减小的趋势,这与轴承内圈圆度检测装置仿真的结果的趋势大致上是一样的,考虑到实验条件的限制,气缸压强0.4MPa以后无法实验,一方面考虑到安全性,另一方面考虑到零件的刚度和强度等因素,并且通过仿真的实验结果可以预测0.4MPa以后在增大气缸压强会增大轴承内圈圆度误差值;分析表2 可知,随着电机转速的增加轴承内圈圆度误差值逐渐减小,这与轴承内圈圆度误差检测的电机转速因素的动力学分析的结果趋势一致,在电机转速3r/s 以前的变化趋势和仿真结果的趋势大致上一致,并且考虑到实验条件的限制,电机转速在3r/s 后再增加,一方面考虑到电机的启动问题,快速启动会对电机本身有一定的影响,并且也会对检测装置造成一定程度的冲击,因此通过仿真的结果可以预测电机转速再增加会对轴承内圈的圆度误差造成增大。
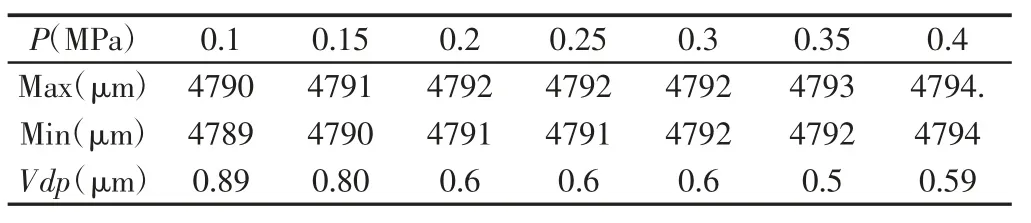
表1 轴承内圈内径圆度的随气缸压强变化的数据Tab.1 Data of Inner Diameter Roundness of Bearing Inner Ring with Cylinder Pressure Change

表2 轴承内圈内径圆度随电机转速变化的数据Tab.2 Data of Inner Diameter Roundness of Bearing Inner Ring with Motor Speed Variation

表3 轴承内圈内径垂直度随气缸压强变化的数据Tab.3 Data of Vertical Degree of Inner Diameter of Bearing Inner Ring with Pressure Change of Cylinder
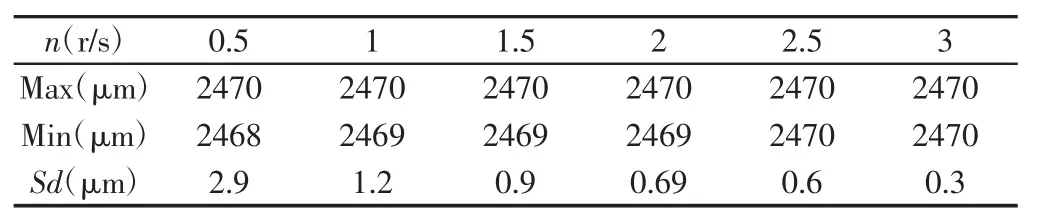
表4 轴承内圈内径垂直度随电机转速变化的数据Tab.4 Data of Vertical Degree of Inner Diameter of Bearing Inner Ring with Motor Speed Variation
分析表3 可知,与轴承内圈圆度误差检测随气缸压强的实验数据分析的结果大致一致;分析表4 可知,与轴承内圈圆度误差检测随电机转速的实验分析数据大致一致。
5.2 轴承内圈沟道壁厚测量的数据验证
同样,保持与在ADAMS 中仿真分析一样的条件下,对轴承内圈沟道壁厚测量的装置进行搭建,并对轴承内圈沟道壁厚进行测量,测量数据,如表5、表6 所示。
分析表5 可知,轴承内圈沟道壁厚的误差值随气缸压强的增大有逐渐减小的趋势,这与在ADAMS 中轴承内圈沟道壁厚检测装置的动力学分析结果比较契合,虽然在仿真结果中有些点的值偏大,但是不影响总体上轴承沟道壁厚随气缸压强增大逐渐减小的趋势;分析表6 可知,随电机转速的增加,轴承沟道壁厚的误差值逐渐减小,ADAMS 中仿真结果也表现出同样的现象,同时还预测了随着电机转速的再进一步增加的现象,也表现出轴承沟道壁厚误差值减小的现象。
以上通过搭建轴承内圈形位检测实验装置,实验的结果与仿真的结果在误差允许范围内,可以认为两者的结果是比较契合的。
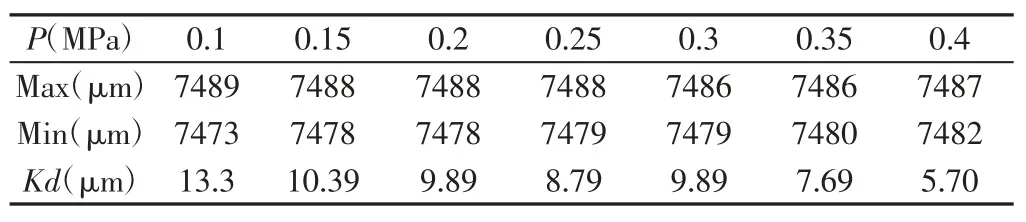
表5 轴承内圈沟道壁厚随气缸压强变化的数据Tab.5 Data of Variation of Groove Wall Thickness of Bearing Inner Ring with Cylinder Pressure
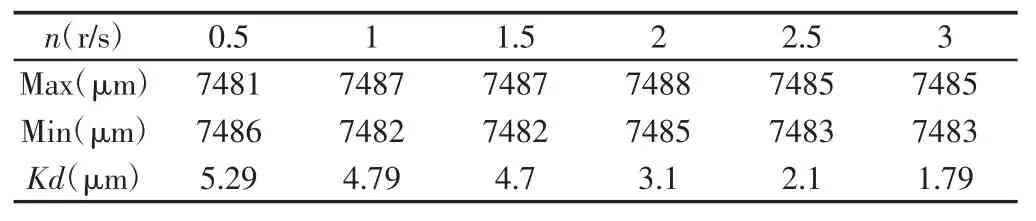
表6 轴承内圈沟道壁厚随电机转速变化的数据Tab.6 Data of Variation of Groove Wall Thickness of Bearing Inner Ring with Motor Speed
6 结论
(1)为了解决轴承智能化生产线上工序间的在线检测问题,为了更好地为轴承下一道检测工序提供反馈信息,设计了轴承内圈参数的综合自动化检测装置。
(2)采用误差分析的方法,对影响轴承内圈参数测量因素进行了误差分析,为轴承内圈检测装置动力学仿真和实验的验证提供了一定的参考依据;利用Solidworks 和ADAMS 联合仿真,并采用Hertz 接触理论对ADAMS 中重要的接触力进行设置,仿真结果表明气缸的压强和电机转速大小对轴承内圈参数测量有很大的影响。
(3)搭建实验平台来验证误差分析和动力学仿真结果的正确性和合理性,实验的测量数据表明轴承内圈参数测量误差确实与气缸的压强和电机转速大小有很大的关系,实验结果和仿真结果相吻合,一定程度上证明了检测装置设计的正确性合理性。

