薄壁圆筒孔径测量误差分析
朱振伟 ,王亚龙 ,张 瑞 ,3
(1.河南机电职业学院机电工程学院,河南 新郑 451191;2.郑州大学机械工程学院,河南 郑州 450001;3.洛阳郑大物联科技有限公司,河南 洛阳 471300)
1 引言
基于工序的智能化生产线内部(产线内)检测是实现产线智能制造的基础要求。其中,粗加工工序的产线内检测往往处于被忽视的地位,但这一环节的质量控制对后续工序生产有着决定性的影响。同时,由于是粗加工,相应的基准尚未建立,这就给检测带来了难度。
薄壁圆筒的精密加工是一个难点,产线内的检测是提高薄壁圆筒加工质量的有效手段。以铸造圆筒钢毛坯来制造薄壁圆筒的第一道加工工序—内孔粗车的线内检测为研究对象,对薄壁圆筒粗加工检测的实现进行研究[1-2]。
2 测量内容要求及原理
铸造圆筒钢毛坯经粗切形成代加工的毛坯,进入数控车进行内孔加工。本道工序加工完成后需检测的内容有:将圆筒工件沿着主轴方向分为三个截面,分别对三个截面的直径进行多次测量,并初步评估圆度。
由于只加工了内径,毛坯端面尚未加工,这就造成了圆筒母线高度不一致,外表面仍是毛坯面的状况。同时由于是产线内部的检测,对检测的节拍和工件的处理也提出了要求。在此条件下,采用激光传感器结合构造的接触式定位基准,搭建了相应的测量原理[3]。
使用两圆柱销定位块限定薄壁圆筒的位置,并在圆筒外侧两圆柱定位销中点连线的中间位置施加作用力,使得圆筒工件中心轴与测量装置轴心线对正平行,实现三点定圆。激光传感器轴线处于三点圆的直径上,传感器后置测头顶销与筒壁接触,由传感器读数即可得到圆筒的内径,如图1 所示。

图1 测量方案原理示意图Fig.1 Schematic Diagram of Measurement Scheme Principle
由于该装置必然存在加工和装配误差,现对装置误差的来源及其对测量结果的影响分析如下。可将两柱定位块等效为圆盘定位块,便于原理说明解析。简化测量原理空间示意图,如图2 所示。
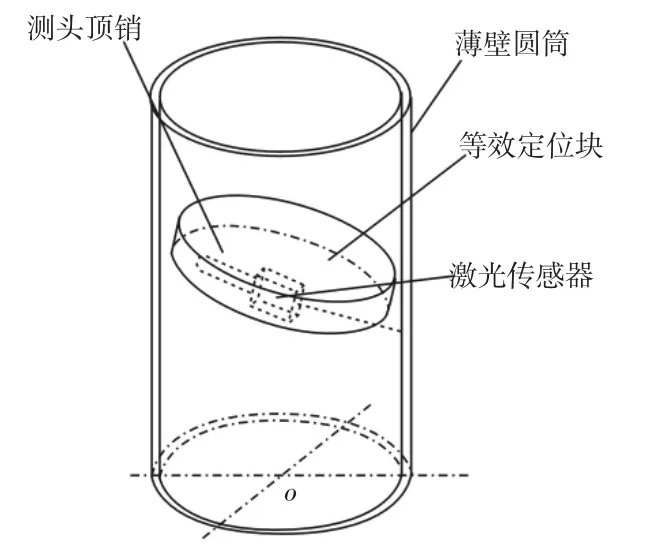
图2 测量装置空间示意图Fig.2 Space Schematic Diagram of Measuring Device
3 数学模型建立
实际测量时,传感器和定位块相对于理想测量位置会发生偏心,倾斜等误差影响因素。针对每种因素单独建立分析模型,并将各模型的分析结果进行叠加,得到整体误差。
理想孔径测量截面示意图,如图3 所示。
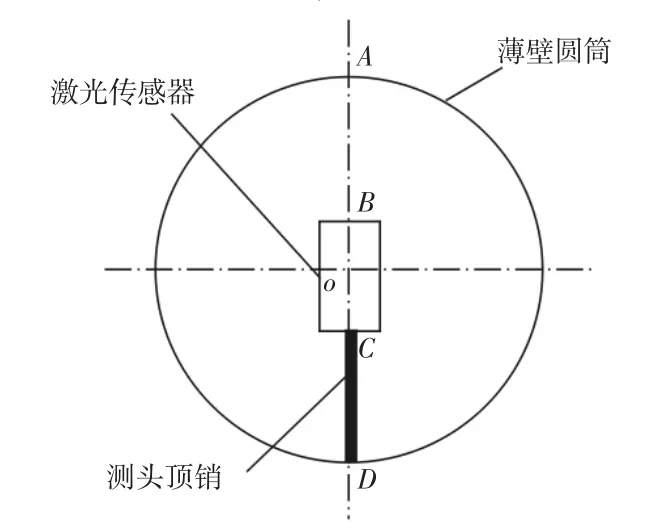
图3 无误差影响因素测量截面图Fig.3 Measurement Sectional View without Error Influencing Factors
设AB 为激光传感器测量值,AB=a;BC 为激光传感器长,BC=b;CD 为测头顶销长度,CD=c,如图3 所示。AD 为传感器测量线,此时,AD=a+b+c。则测量误差,如式(1)所示。

式中:d—直径实际测量值;d0—理想圆筒直径值。
(1)当传感器发生平移偏心时,测量截面示意图,如图4 所示。设实际测量直径距离理想直径AD 偏心距为OO1,OO1=e,由于偏心方向对结果的影响是一样的,因此e>0。

图4 偏心测量截面图Fig.4 Measurement Sectional View of Eccentricity
此时直径实际测量线是A1D1,设其值为d1,则:

带入式(1):

式中:当 e 为 0 时,d1=d0,δ1=δ0。
(2)当传感器在有偏心距的基础上发生水平面上的倾斜时,测量截面示意图,如图5 所示。

图5 水平面上倾斜测量截面图Fig.5 Inclination Measurement Sectional View on Horizontal Plane

图6 垂直平面上倾斜测量截面图Fig.6 Oblique Sectional View of Vertical Plane
传感器偏心距离e 后,传感器测量线D2A2绕D2点旋转角度β,由于定位块的限制D2A2的旋转方向是单向的,故β>0°。此时直径实际测量线A3D2,设A3D2=d2,则:


式中:β=0 时,d2=d1,δ2=δ1。
(3)当传感器继续向上发生垂直方向的倾斜时,测量截面图,如图6 所示。
测量线D2A2在垂直面上绕A3点逆时针旋转角度γ,得到测量线A3D3,由于A3D3顺时针旋转与逆时针旋转角度关于A3D2对称,旋转方向对结果影响一样,因此γ>0°。此时直径测量线为A3D3,设 A3D3=d3,则:

式中:γ=0 时,d3=d2,δ3=d2。
(4)在以上几种影响因素下,测头顶销安装发生偏折角度α,由于偏折方向对结果的影响是一样的,因此α>0°。顶销尺安装偏折截面图,如图7 所示。
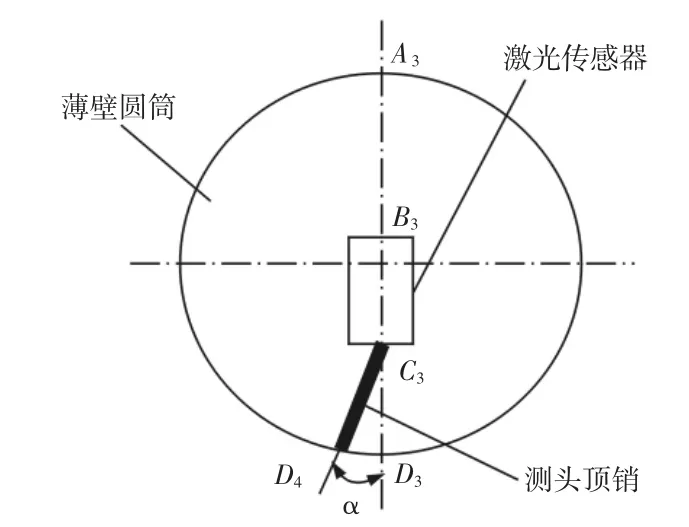
图7 安装偏折测量截面图Fig.7 Measurement Sectional View of Installation Deflection
实际直径测量线为折线A3C3D4,测量值d 变化,主要是由顶销顶到内壁位置偏移变化引起,垂直距离缩小,而c 值为标定的固定值,但是这一段缩短的值Δc 被激光传感器测量距离值a 补偿。设此时测量直径值为d4,则:

相对于测量直径,就会多出补偿值Δc。

带入式(1),则:

通过以上分析,建立的综合误差模型公式为:

4 实例模型求解验证
4.1 影响因素变量范围的确定
在实际工程应用中,以某薄壁圆筒缸套为实验对象,加工误差要求0.1mm,测量误差要求0.05mm。根据测量装置的结构尺寸,圆盘定位块直径80.80mm,高度41.8mm。偏心距e 根据定位块的位置限制,其定义域为0≤e≤0.30mm,β、γ 两角的范围,根据定位块在圆筒工件中的最倾斜位置角度确定为-0.40°≤β≤0.40°,0°≤γ≤0.40°。测头偏折角度 α,根据安装表面的精度,包括平行度和垂直度要求,分别取6 级精度、7 级精度和8 级精度,通过公式计算,得到分别取三个值 α1=0.43°,α2=0.55°,α3=0.65°。转化为求解数学模型的最优解问题[4-7]。
4.2 采用MATLAB 进行求解
目标函数为式(12)。
根据测量装置实际结构尺寸得,d0为81.1mm,c 为6.95mm。
约束条件如下:0≤e≤0.30mm;0≤β≤0.40°;0°≤γ≤0.40°;α1=0.43°;α2=0.55°;α3=0.65°。
在MATLAB 中使用Colormap 等函数可分别得到α1=0.43°,α2=0.55°,α3=0.65°下的误差范围立体图像,如图8 所示。

图8 三个分别对应的误差范围立体图Fig.8 The Error Range Stereogram of Three
如以上三图所示,孔径误差三维立体分布示意图,三个坐标轴分别代表三个变量e、β 和γ,图上数据点的颜色代表孔径误差值的大小,图右的图例显示对应颜色的数值大小。根据图示可得孔径误差有正有负,变化趋势呈扇形辐射,逐层增减。需要提取精确解,对孔径误差范围进行定量分析[8]。
在 MATLAB 中的使用 max 和 min 函数,分别得到 α1、α2、α3对应直径误差最大值δmax最小值δmin,如表1 所示。
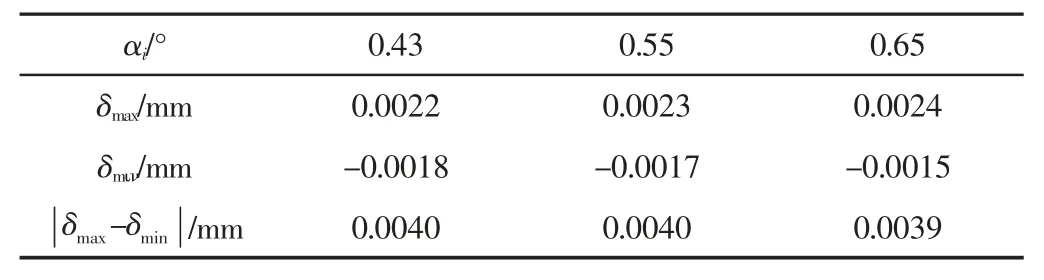
表1 不同值对应的孔径误差Tab.1 Aperture Error Corresponding to Different Alpha Values
如表1 所示,孔径误差范围保持在0.0040mm 内,远远小于工程要求的精度范围0.05mm,所以上述建立的模型符合工程要求。
5 实验数据验证
通过以上模型的建立和求解分析,可得使用圆盘定位块限定传感器的轴心与工件圆筒的轴心的相对位置,保证圆心定位精度从而测量圆筒工件的直径的方案在理论上是可行的,但是需要进行实验,并通过分析实验数据进行验证[9-10]。根据方案原理,建立工作实验台。实验中确定零部件表面精度都为8 级,实验装置,如图9 所示。

图9 孔径测量实验装置图Fig.9 Experimental Setup for Aperture Measurement
使用如图9 所示的装置,在对测头顶销标定后,将直径为81.1mm 的圆筒工件任意放置在工作台上,通过气缸传动引导定位块对圆筒工件进行定位和对准测量基准线,外加作用力使得定位块与圆筒工件内壁紧贴。由单激光传感器读数即可得到测量的内径值,在圆筒工件中选取某三个截面作为测量面,利用本实验装置对该测量面进行扫描测量,并重复实测,共测量50 组数据,统计孔径测量数据,将数据绘制折线图,如图10 所示。

图10 实测孔径误差折线图Fig.10 The Line Chart of Measured Aperture’s Error
数据结果显示误差稳定在-0.01≤δ≤0.006mm 范围内,误差范围控制在0.004mm 内。这与在MATLAB 中通过对数学模型求解计算的结果对比,误差值具有一定的偏差,但是误差范围相等。通过分析,在实际的测量过程中,整个测量系统引入的格外的误差,而在模型求解过程中对一些因素采用理想化处理,近似代替等等方式,从而使实测误差值偏大,但是误差稳定在工程要求范围内。而实测的误差值也符合工程要求。
6 结论
在利用单激光传感器扫描测量圆筒工件内径过程中,通过定位块将测量装置测量基准与圆筒工件中心轴线对齐,则影响内径测量误差的主要因素就由单激光传感器在圆筒工件中的位姿决定,单激光传感器的位姿越接近理想位姿,孔径测量精度就越高。通过研究影响薄壁圆筒直径测量误差的各种单因素的综合关系,建立数学模型,使用MATLAB 计算以及实验数据验证分析,得到以下结论:
(1)通过类似圆盘形定位块圆盘定位块限定传感器的轴心与工件圆筒的轴心的相对位置,保证圆心定位精度从而测量圆筒工件的直径的方案是可行的。计算精度和实测精度都达到工程需求的0.05mm。
(2)传感器在圆筒工件内的任意位姿测量内径时,各个变化的几何影响因素相互叠加在一起综合考虑对孔径测量误差分析是不可忽略的。
(3)上述模型建立与计算推导可为气缸套等圆筒类零件的加工制造提供误差控制理论的支持。
(4)对于影响圆筒类内径测量误差的不方便控制因素,可以转化为测量装置的方便计算和控制的变量,通过建模求解和实验分析对该测量装置的测量精度进行验证。

