基于最小能耗的沥青路面就地热再生加热机组优化控制

段宝东，韩东东，赵永利

(1.江苏宁宿徐高速公路有限公司，江苏 宿迁 223800； 2.东南大学 交通学院，江苏 南京 211189)

0 引言

沥青路面就地热再生技术具有节约资源、保护环境、节省公路养护费用及施工速度快对交通的干扰小等优点[1-2]，可实现再生层与其下承层间热黏结,从而提高沥青路面面层结构的整体性，具有显著的经济效益和社会效益，目前已成为沥青路面的最佳养护方式之一[3-4]。就地热再生是一项高度集成化的沥青路面养护技术，旧沥青路面的加热、翻松及再生混合料的拌和、摊铺、压实等在现场一次性完成，这其中最为关键的就是旧路面的加热过程[5]。因为旧路面只有被加热到规定温度，旧沥青混合料才能在不破碎骨料的前提下被充分分解并与添加的再生剂、新沥青混合料等充分融合[6-7]；再生剂只有在适宜的温度条件下才能与旧沥青充分混溶，从而恢复其性能[8-10]；再生混合料要有足够的温度才能摊铺均匀和被充分压实[11]。但是，单纯通过增加加热功率来确保路面加热温度，必然带来燃料消耗、养护成本及排放的增加。

国内外已有学者对沥青路面就地热再生加热过程进行了研究。李雪毅等[12]模拟了热风循环加热温度场，并指出路面各层温度随加热时间的增加而升高，路面深层的温度变化呈现明显的滞后性。顾海荣等[13]建立了沥青路面加热温度场数值模型，提出了多步法加热施工工艺，与传统单步法加热工艺相比，沥青路面加热到相同温度时，可节省43%的时间，所需能量仅为单步法的70%；张德育等[14]通过有限元数值模拟分析了加热方式、环境温度、加热功率、加热速度等因素对旧路面温度场的影响。Xu等[15]通过传热学理论，提出了恒温变功率加热方式，并且给出了理想的热流密度曲线，有效地杜绝了过加热现象的出现。郭小宏等[16]通过建立一维瞬态传热模型，研究了沥青路面就地热再生多级加热技术，认为采用二级或三级加热模式较合理。

尽管上述研究对就地热再生加热工艺有了一些改进措施，但都没有考虑实际加热机组对路表的热作用强度，计算的温度场与实际情况相差较大，不能够很好地指导实际工程的施工。

本研究依托就地热再生实体工程，首先建立沥青路面一维传热模型，通过现场埋置温度传感器获得路面各深度的温度数据，反演计算加热机组对路表的辐射热流强度，并将遗传优化算法与传热模型相结合寻找加热机组在不同运行速度下的最优组合，研究结果既能满足旧路面铣刨温度要求，也能最小化能量的消耗，为就地热再生加热机组控制提供了理论基础。

1 就地热再生路面加热一维传热模型建立

在沥青路面就地热再生施工加热阶段，加热机通过对再生路表面施加一定强度的热流，使得路面上部结构温度升高，与下部结构存在温度差，热量总是从温度较高的路面上部层位传递给温度较低的下部层位，从而实现整个再生层的加热，热量传递主要发生在路面结构上、下相对位置之间，因此，对于沥青路面加热，可以认为是沿路面深度方向的一维传热。

为建立沥青路面传热模型，从沥青路面中取出一个六面体微单元，如图1所示。在沥青路面加热时，每个六面体微单元的热量交换，都可以概括为微单元表面热量的输入和输出以及自身内能的变化。

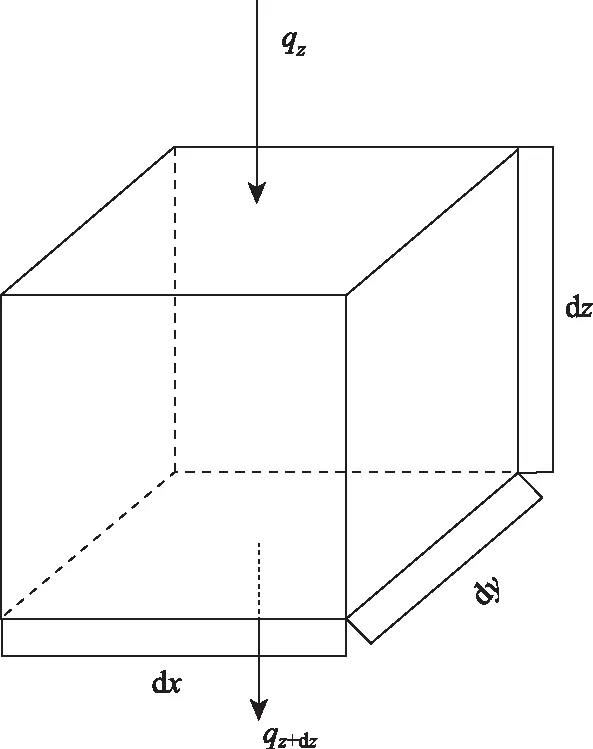
图1 沥青路面一维传热模型Fig.1 One-dimensional heat transfer model of asphalt pavement

根据能量守恒定律，微单元热量输入及输出应满足自身内能的变化：

(1)

式中，ρ为微单元密度；c为微单元的比热容；dx，dy，dz为微单元x，y，z方向的边长；T为温度；q为微单元表面的热流密度。

化简为：

(2)

对一维瞬态传热微分方程的求解，可以采用向前差分原理，空间域按Δz等份离散化，时间域按Δt等份离散化，公式(2)可以离散化为：

(3)

因此，第i个空间节点在(m+1)Δt时刻的温度如下：

(4)

根据傅里叶导热定律：

(5)

(6)

式中，q0为路表净热流密度；ki为第i个节点的导热系数。

2 加热机热流密度反演计算

2.1 现场施工温度数据获取

本研究对某高速公路K162+50-K161+850段进行路面温度监测，采集不同加热功率下的路面温度数据，试验选用3台加热机分别对应3次加热，每台加热机长度为20 m，相邻机组间距为3 m，加热机组的运行速率为3 m·min-1，按照先后顺序依次对路面进行加热，加热机的功率与开启的加热枪嘴的数量有关，将每台加热机加热枪嘴的数量定为4个和2个，以对应大功率和小功率。选取2个断面，在每个断面钻取不同深度的钻孔，钻孔深度分别为2.0，3.5，4.5，5.5，7.5 cm，在每个钻孔分别埋置温度传感器，传感器埋设位置及路面结构如图2所示。

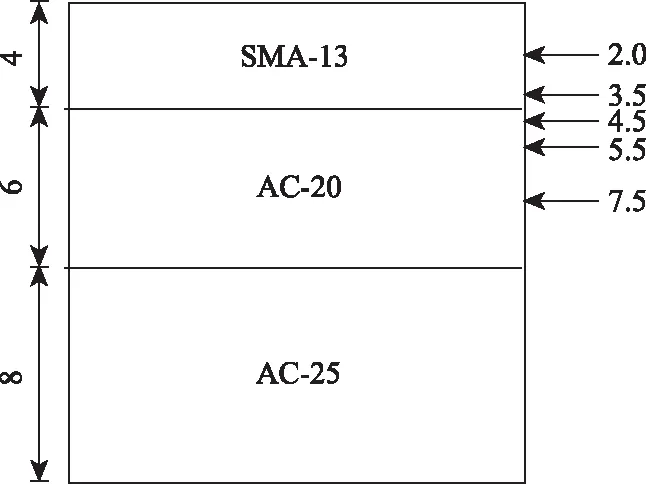
图2 传感器埋设位置及路面结构(单位：cm)Fig.2 Sensor embedded positions and pavement structure(unit:cm)

每台加热机机尾后1 m处实测温度如表1所示。在同一断面，随着加热次数增加，各层温度均有所提高；随着深度增加，温度急剧下降；路面z方向温度梯度较大，且随着深度增加，温度梯度逐渐减小。对比不同桩号温度，大功率下对应的路面各层温度较小功率高。

表1 不同功率下实测温度Tab.1 Measured temperatures under different powers

2.2 加热机辐射热流密度反演计算

传热方程未知参数有路面结构层热物性及加热机作用在路表的辐射热流密度，路面材料热物性参数见表2[17-18]。

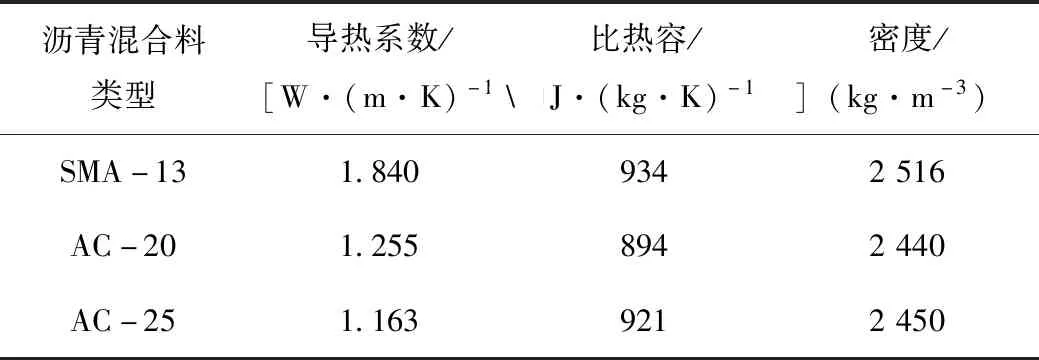
表2 路面结构层热物性参数Tab.2 Thermal parameter of pavement structure layer

实际施工中，加热机的功率是通过喷嘴数量来控制的，而加热机辐射热流密度无法在施工现场直接获得，为了后续计算，将通过已经建立的一维传热模型拟合实测温度数据，从而反演计算加热机最大、最小功率的辐射热流密度。其中单台加热机组采用间断式的加热方式，总共由3个加热器组成，第1个和第3个加热器长度为3 m,第2个加热器长度为6 m，第1与第2及第2与第3个加热器距离均为4 m，故加热机总长度为20 m，因此单台加热机对路表的作用可以简化为图3所示的热流密度随时间的变化。

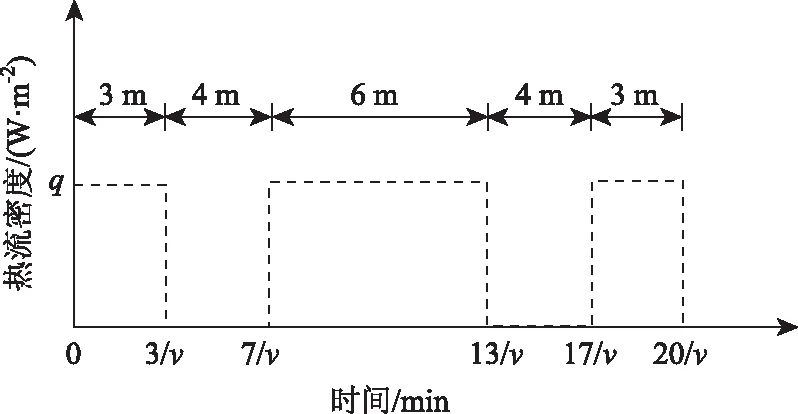
图3 单台加热机对路面某断面辐射热流密度Fig.3 Radiant heat flux density of single heating unit to a section of pavement

分别选取表1中不同功率下的温度数据独立进行计算，在传热模型中，为了与实际工况相对应，图3中速度v取3 m/min，且施加3次图3中的热荷载以对应实际3台加热设备，荷载施加间隔为60 s以对应加热设备3 m间隔。因此从第1台加热机开始加热至最后1台加热机结束且温度测试完毕所需要的总时间为1 340 s。拟合计算结果如图4所示，可以看出最大、最小功率下的实测温度与数值模拟结果较吻合。计算的加热机最大、最小功率对应的热流密度分别为18 555 W/m2和25 600 W/m2。同时可以看出实测温度与数值模拟结果相辅相成，虽然实测关键点温度数据不能完全反映整个加热过程温度的变化情况，但其可以作为拟合传热模型的数据，通过拟合得到的数值结果来反映加热过程中各层温度随时间的变化。其中路表面温度变化波动起伏较大，这是由于加热机采用间断式加热方式，使得各加热机加热完毕后过高温度的路表通过空气对流及热辐射方式向外界释放热量，达到冷却的目的，避免形成连续集中的加热条件，防止路表出现过加热现象。

图4 不同功率下拟合结果Fig.4 Fitting result under different powers

3 基于遗传算法的加热机组优化控制

在很多情况下，由于加热机控制不合理，使得现场加热温度不能满足就地热再生温度的要求，导致矿料级配细化；但如果盲目提高加热机功率，将会使得路表出现过加热现象，同时也会消耗更多的化石燃料，这不符合就地热再生节能环保的初衷。因此本研究采用遗传算法结合一维传热模型，寻找加热机不同运行速度下，加热机组辐射热流密度的最佳组合，使得旧路面既能满足铣刨温度要求，又能最小化能量的消耗，为就地热再生加热机组施工控制提供参考。

3.1 遗传算法

遗传算法是模拟自然界生物进化过程的一种寻找全局最优解的优化算法[19]。在寻找就地热再生加热机组最优组合过程中，遗传优化算法结合一维传热模型的主要步骤如下：

(1)初始化种群：第1、第2及第3台加热机辐射热流密度分别为q1，q2，q3，每1种加热机组功率的组合q1(i)，q2(i)，q3(i)在遗传算法中都代表了1个个体i。由于加热机功率的限制，加热机对路表辐射热流密度范围取为18 000～26 000 W/m2，初始种群数量设置为100，并通过随机算法生成。

(2)适应度计算：适应度是用来衡量每个个体对环境的适应能力。为了能够寻找既能满足铣刨温度的要求又能最小化能量消耗的热通量组合，个体适应度fitness(i)计算公式如下：

(7)

式中，Tbi为第i个个体再生层层底温度；Q为惩罚因子，取10 000。

总热流密度越大，说明加热机总功率越大，消耗的能量也就越大，适应度就越低。同时每个个体i也要代入传热方程，检验其再生层温度Tbi是否满足要求。舒琴等[20]指出，当整个再生层温度达到90 ℃时，可以有效减少集料的破损。考虑到现场沥青路面加热特点是热量从上往下传递，路面上部温度总是高于下部温度，当再生层层底温度达到90 ℃时，整个再生层的温度也都能满足铣刨的要求。因此，当Tbi大于或等于90 ℃时，该个体满足铣刨温度要求，适应度为总热流密度的倒数；当Tbi小于90 ℃时，该个体不满足铣刨温度的要求，本研究对不满足铣刨温度要求的个体施加惩罚函数(90-Tbi)×Q，该函数表示再生层底的温度Tbi离90 ℃越远，适应度越小。

(3)选择和繁衍：轮盘法是以适应度大小作为被选择到下一代的概率selection(i)，由式(8)计算，按此方法选择具有相同数量的下一代种群。

(8)

(4)变异与交叉：图5为某个个体的2号染色体发生的突变及交叉。本研究中，每个个体染色体的交叉和变异概率均为0.02。

图5 染色体变异及交叉Fig.5 Chromosome variation and crossover

(5)得到最优解：当初始种群不断按照步骤(2)～(4)进行循环迭代时，整个种群的平均适应度不断得到提高，直到保持稳定，此时种群中最优适应度对应的个体即为最优解。

3.2 不同运行速度下加热机辐射热流密度最优组合

就地热再生作业速度通常在2～4 m/min之间。图6为速度间隔取0.1 m/min时，遗传算法优化的结果，可以看出在较低运行速度2.0～2.3 m/min，即使3台加热机的热流密度都取最小值18 000 W/m2，对应的再生层层底温度也都能达到90 ℃以上。当加热机运行速度增加至2.4～3.2 m/min 时，加热机采用最小辐射热流密度已经不能满足铣刨温度的要求，此时加热机热功率需要升高，根据最小能耗的原则，再生层层底温度刚好达到90 ℃时所消耗的能量最小。当运行速度达到3.3 m/min及以上时，3台加热机热流密度分别达到最大值26 000 W/m，但此时再生层层底温度均低于90 ℃。这说明当运行速度过大时，即使加热机保持最大输出功率，加热完毕后的温度仍无法满足铣刨要求。因此，为满足就地热再生加热温度要求，加热机运行速度应该小于等于3.2 m/min。

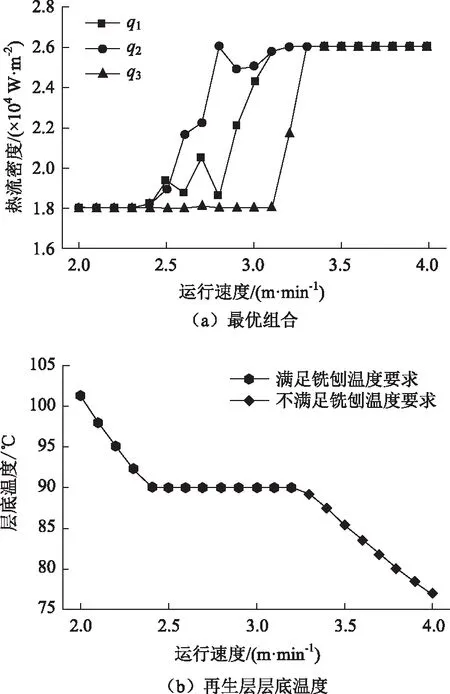
图6 不同运行速度下最优组合Fig.6 Optimal combination at different operating speeds

同时从图6(a)中可以看出，在最优加热机组热流密度组合中，q2即第2台加热机的辐射热流密度最大，q1次之，q3最小。产生这种现象的原因由于加热过程热量的散失以及热量传递的滞后性导致，在第1台加热机对某一断面加热完毕后，还需要用第2台、第3台加热机进行加热，在此过程中还需要经过相当长的时间才能完成加热。第1台加热机对路表作用的热量尽管有一部分传递到路面下部层位，但是仍有相当部分热量散失到大气中，因此优先增加第1台加热机功率会导致热效率的降低；在第3台加热机加热完毕后，由于沥青路面热量传递的滞后性，第3台加热机对路面作用的热量还没完全下渗到更深路面层位，因此不宜优先增加第3台加热机的功率；第2台加热机处于第1与第3台加热机之间，热量散失较第1台少，热量的渗透性较第3台高，从图中还可以看出，相较于第3台加热机，提高第1台加热机功率具有更高的热效率。因此在实际的就地热再生施工过程中，3台加热机先以最小功率进行加热，若加热温度不满足要求，按依次优先增加q2，q1，q3的原则，即优先提高第2台加热机的功率直至满足加热温度要求，若第2台加热机功率达到最大值时仍不满足加热温度要求，继续按照q1，q3优先原则依次提高第1台和第3台加热机的功率直至加热温度满足要求。

考虑能量消耗时，本研究分别计算了不同运行速度加热机组最优组合下加热1 000 m路面的总能耗，如图7可以看出，每台加热机加热1 000 m路段的总加热距离为1 020 m。因此，最优组合下3台加热机的总热流密度(Total heat flux,THF)及加热1 km 的总能量消耗(Total energy consumption,TEC)计算公式分别为式(9)，式(10)。

图7 每台加热机加热1 km加热距离(单位：m)Fig.7 Heating distance per kilometer for each heating unit(unit:m)

(9)

(10)

式中A为单台加热机加热器总面积。

图8为最优组合下的总热流密度及总能耗，在较低运行速度2.0～2.3 m/min下，总辐射热流密度最低，虽然加热机组总功率最小，但由于运行速度较低，延长了加热机加热的时间，反而导致总能量消耗较大，由图6(b)可以看出，此时的再生层层底温度高于要求的90 ℃，表明能量富余了。当运行速度增加到2.4～3.2 m/min时，此时加热机的功率可根据运行速度进行调整，随着速度的增加，功率相应增加；总功率虽然增大，但是速度的增加缩短了加热机加热的时间，每公里的总能量消耗反而较小，尤其运行速度在2.4～3.1 m/min时，总能量消耗基本保持在6.6×1010J左右。当运行速度超过3.3 m/min时，最优组合下的总能耗逐渐降低，但是此时加热机的总热流密度已达到最大值，其加热温度却不能满足铣刨温度的要求(如图6(b)所示)。

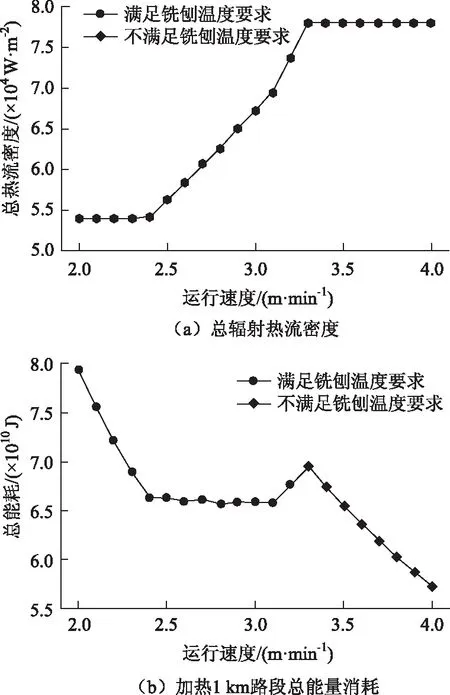
图8 最优组合下总热流密度及能耗Fig.8 Total heat flux density and energy consumption under optimal combination

因此，适宜的施工加热机运行速度应在2.4～3.1 m/min之间，此时不仅可以满足再生层层底加热温度的要求，同时加热过程消耗的总能量能够达到最小。

4 结论

(1)本研究依据固体传热理论及再生沥青路面加热特点，建立了沥青路面就地热再生加热过程的一维传热模型，并且与实测现场温度进行拟合，拟合结果较吻合。

(2)在沥青路面就地热再生加热阶段，温度的散失及温度传递的滞后性将会影响到加热机组热效率，按照最小化能耗的加热原则，3台加热机应先以最小功率进行加热，当需要提高加热机加热功率时，应优先增加第2台加热机的加热功率，然后是第1台，最后是第3台。

(3)为满足沥青路面就地热再生加热温度要求，加热机运行速度应该小于等于3.2 m/min，同时加热机运行速度在2.4～3.1 m/min之间时，加热过程的总能耗能够达到最小。

(4)在就地热再生实际施工中，结合结论(2)和结论(3)的控制方法，控制机组速度范围在2.4～3.1 m/min，按照第2台、第1台、第3台次序依次增加加热机功率，从而满足加热温度且最小化能耗。