大跨度斜拉桥车桥耦合振动响应的影响分析

黄志和，张天天，罗苑

（重庆建工高新建材有限公司，重庆 401122）

0 引言

近年来，我国交通网发展速度明显加快，在建和拟建的大跨度公路桥梁的数量明显增加。随着桥梁跨度不断增长，其柔性增大，对外部的车辆荷载激励更加敏感。国内外相关专家和学者在这方面做了大量的研究。其中以西南交通大学李永乐、长安大学韩万水为代表的专家团队在公路桥梁行车分析方面做出了重要贡献。李永乐团队针对桥上不同类型移动车辆、双车交会以及风-车-桥系统评价等方面做了大量的探索[1-2]。韩万水团队提出用梁格法分析模型中汽车和桥梁耦合振动关系，并给出了修正过程和验证结果[3]，随后在此基础上进行了随机车流下精细化的车桥耦合振动分析，并实现了随机车流过桥动态可视化[4]。部分学者还对桥上行车舒适性、考虑车辆荷载的锈损桥梁疲劳性能、随机车流下桥梁振动情况进行了研究[5-8]。从国外来看，D.Rocchi等[9-10]通过包含刚性和柔性的多体动力系统模拟车辆，对桥塔附近有无风障的工况进行了多次重复风洞试验，分析了有驾驶员参与模型的车辆穿过桥塔时车桥耦合振动情况。Wei Zhang等[11]提了基于EOMM仿真方法的多尺度动力自由度建模方案，将桥梁简化单元与精细单元放在相同的位置，精确分析了在车辆作用下桥梁整体和局部的静态和动态响应。Ivica Kozˇar等[12]运用谱方法中出色的矩阵运算能力，并将其应用到车辆和桥梁的振动中，实现了在移动荷载下桥梁振动状况的高精度模拟。

基于以上汽车-桥梁系统方面的迭代计算研究方法，本文对强风作用下的车辆-桥梁模型进行了简化，建立了该桥的有限元模型和多自由度车辆分析模型，通过三角级数法模拟路面粗糙度，路面粗糙度为车辆振动的激励源，形成了车辆-桥梁耦合振动系统，分析了不同车速下大跨度公路桥车辆-桥梁系统振动情况。

1 车辆-桥梁动力学模型的建立

1.1 路面激励

路面激励根据路面等级取值，每个轮胎下输入的路面粗糙度可根据时间确定。当车辆在A级道路上行驶时，所受的路面粗糙度激励如图1所示。

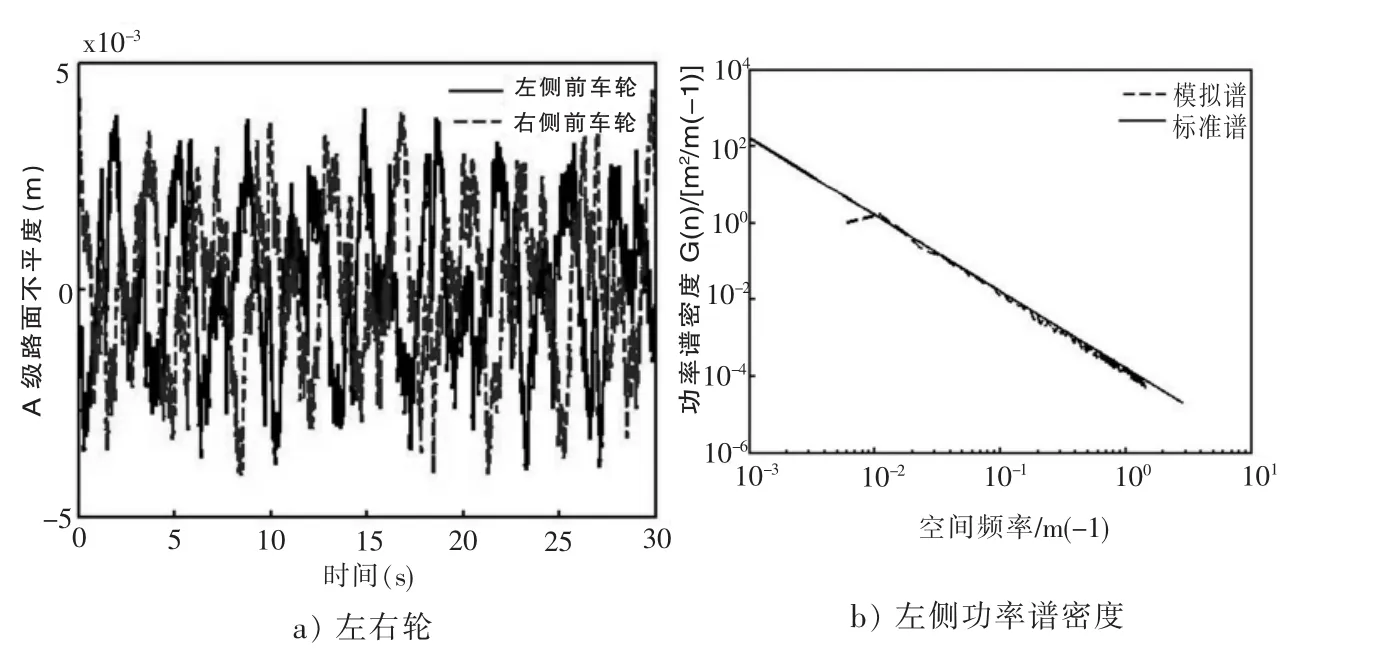
图1 路面粗糙度

1.2 车辆-桥梁动力系统模型

对于车辆-桥梁动力系统模型采取分别研究的方法，两个子系统之间通过车轮与桥面的接触连接。

本文的建模研究基于四个假设。

假设1：通过桥梁的车辆均为两轴车辆，两轴车辆振动模型如图2所示。

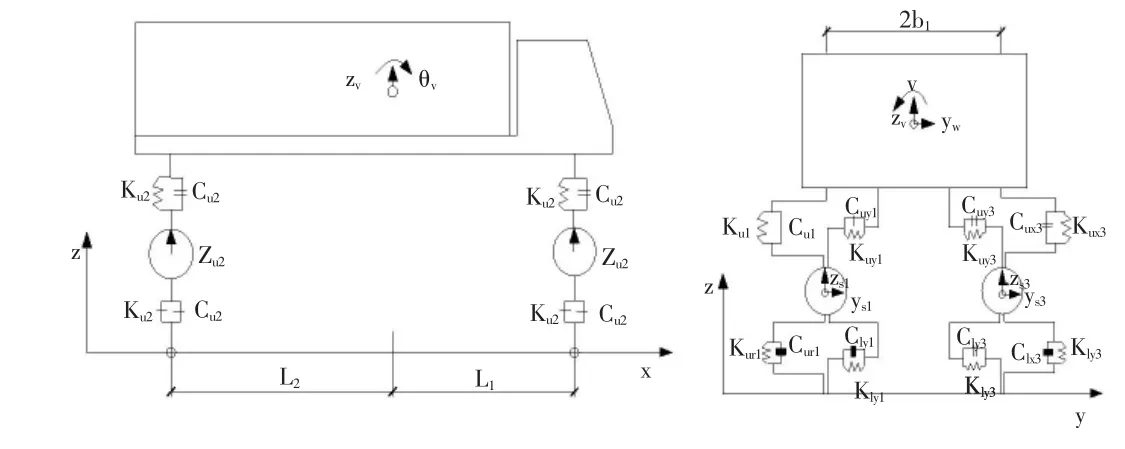
图2 两轴车辆振动模型

假设2：同时位于桥梁上的车辆数量为N，车辆的子系统为N个相互之间无连接但通过桥梁子系统耦合的多刚体系统。

假设3：车辆通过桥梁时，以限定最高速度匀速通过。

假设4：车辆通过桥梁时，车辆轮胎与桥梁在侧向不发生位移。

车辆-桥梁系统计算具体步骤如下：（1）对于时间步t，将前一时步桥梁运动状态)作为初始迭代值，组合 t时刻的路面不平度，形成等效路面不平度；（2）根据等效不平度求车辆受到的作用力 Fbv；（3）根据 Newmark积分法求 t时刻车辆的响应（u¨（4）计算车辆对桥梁的作用力 Fvb；（5）根据 Newmark 积分法求t时刻桥梁结构的响应：①根据t前一时刻桥梁结构的响应（，求当前时刻桥梁自激力 Fseb；②形成荷载列阵，用 Newmark 积分法计算 t时刻桥梁的响应；③根据桥梁t时刻的响应，重复循环直至桥梁响应满足精度要求；（6）根据t时刻桥梁的响应，重复步骤（1）—（6）直至桥梁的响应满足收敛要求，再进行下一时步的计算。

2 车辆-桥梁动力学模型的求解

2.1 桥梁动力特性

本文以某大跨公路桥梁为工程背景进行分析，其跨径布置为68m+68m+79m+720m+79m+68m+68m，主梁为扁平流线形钢箱梁，桥的立面布置如图3所示。

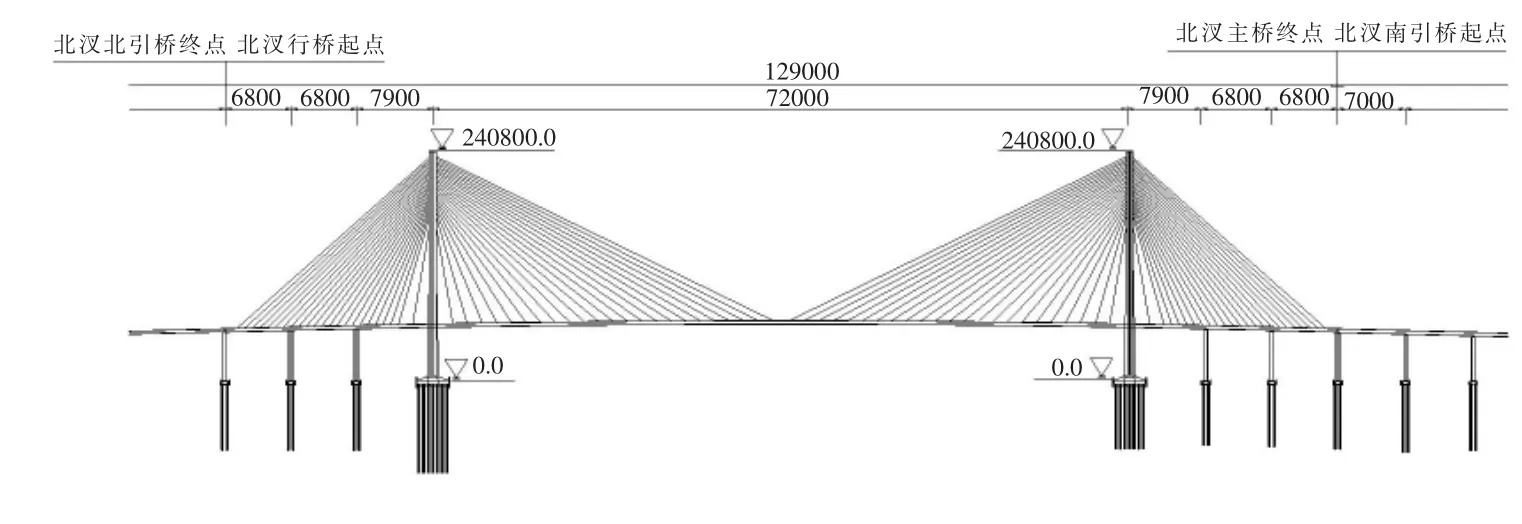
图3 立面布置图（mm）

在ANSYS中建成的主桥有限元模型如图4所示。斜拉索采用了索单元link10模拟。塔、梁及墩等构件采用了beam44模拟，主梁采用了鱼刺骨模型。塔、梁纵向通过combin40连接。表1为主桥前16阶模态频率和振型特点描述。主桥第1阶和第5阶模态振型如图5所示。

图4 有限元模型

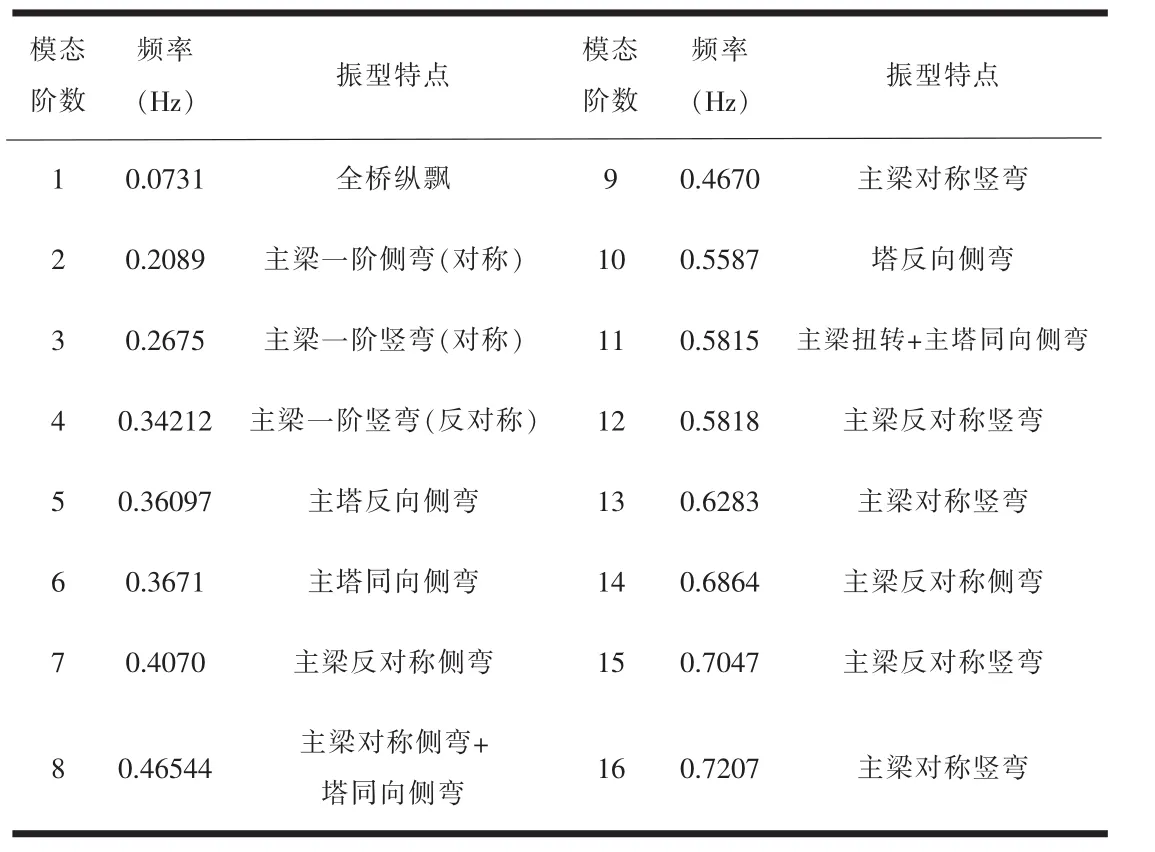
表1 动力特性

2.2 车速影响

本文选取四种车速进行分析，分别为100km/h、80km/h、60km/h、40km/h。桥面粗糙度为A级，车型为厢式货车，车辆数目为十排，车辆间距为10m，车辆上桥之前经过100m路面，时间步长为0.01s。 图 6 为 100km/h、80km/h、60km/h、40km/h 四种车速下主梁跨中竖向位移变化对比情况。

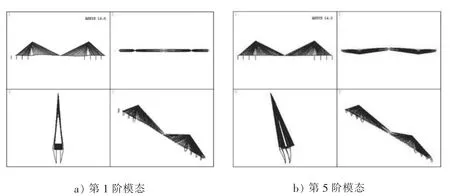
图5 主桥前10阶部分模态振型

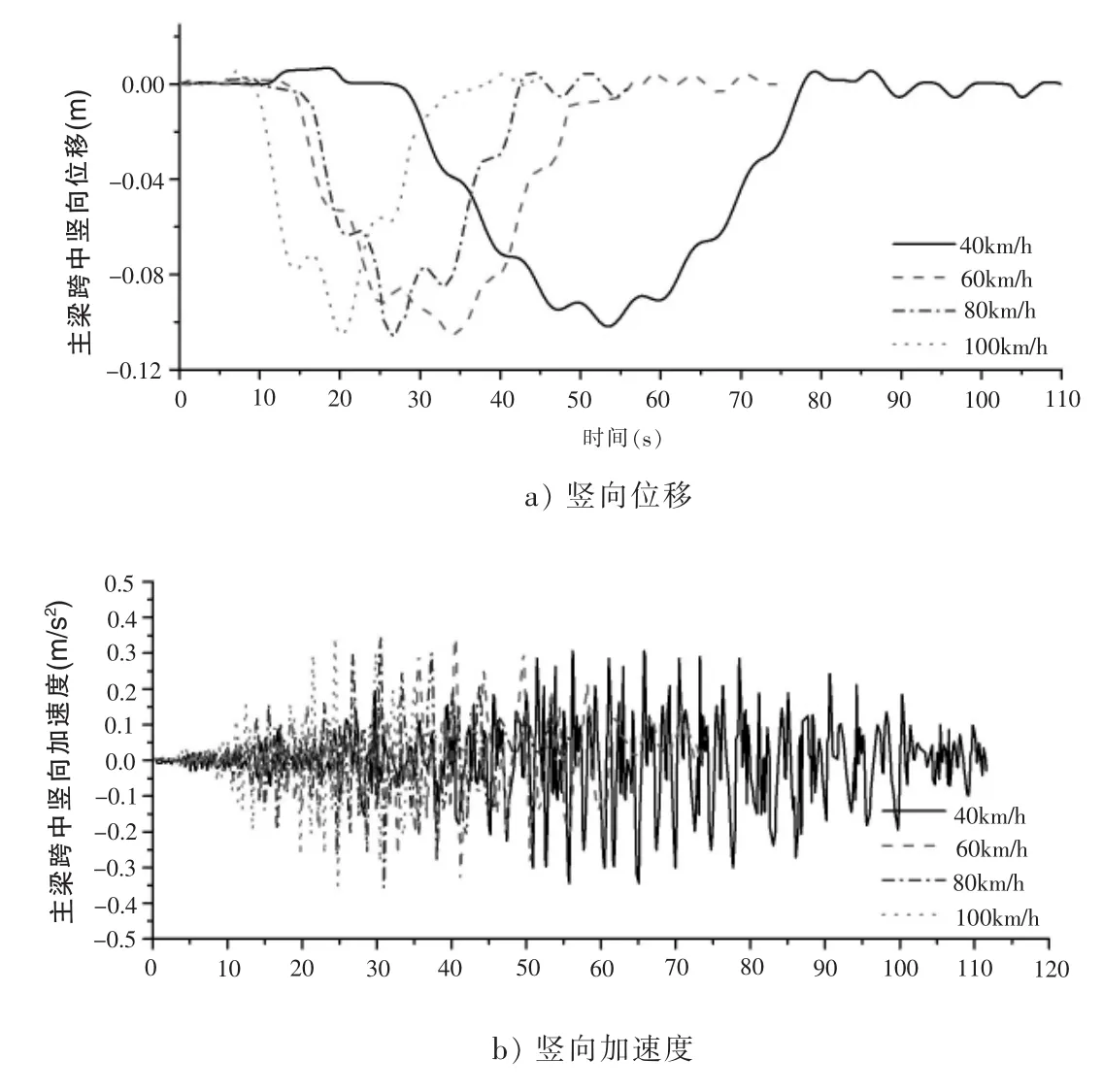
图6 四种车速下跨中响应

由图6可知：（1）当车辆上引桥时，跨中节点基本没有振动。桥梁跨中位移随着车辆靠近而增大，随着车辆的远离而逐渐减小。（2）车辆在靠近和远离跨中的过程中，其位移基本呈对称状态，车辆远离跨中时位移响应恢复较快，车辆靠近跨中过程中，主梁跨中波动幅度小于车辆远离跨中的过程。（3）主梁跨中的加速度随着车辆靠近而增大，随着车辆远离而减小，车辆靠近跨中和远离跨中时，跨中节点加速度基本呈对称状态。主梁跨中位移和加速度的整体变化趋势表明，车辆影响了斜拉桥的局部动力响应。（4）不同车速下主梁跨中位移变化趋势基本一致。车辆在引桥上行走时，跨中节点基本没有振动。（5）当车队头车到达主梁时，跨中出现明显振动，且振动幅度较大，位移主要是向下，直至车队尾车离开跨中。主梁跨中加速度随着车辆向跨中移动而不断增大，车队头车到达跨中时基本会达到极值，之后随着车辆的远离逐渐减小。主梁跨中位移和加速度的整体变化趋势表明，车辆影响了斜拉桥的局部动力响应。（6）不同车速下主梁跨中的最大竖向位移分别为0.104m、0.106m、0.105m、0.103m， 跨中的冲击系数分别为 1.127、1.138、1.125、1.106，跨中竖向位移随着车速的增加有增大趋势，但并不是一直无限制增大。

3 结论

本文采用有限元软件建立了大跨度公路桥模型，并对其进行了模态分析和时程分析，分析了不同车辆速度下桥梁跨中的位移及加速度响应情况，得到如下结论：

（1）车辆靠近跨中和远离跨中时，跨中节点位移基本呈对称状态，车辆远离跨中时位移响应恢复较快，车辆靠近跨中过程中，主梁跨中波动幅度小于车辆远离跨中的过程。

（2）主梁跨中的加速度随着车辆靠近跨中而增大，随着车辆远离跨中而减小，车辆靠近跨中和远离跨中时，跨中节点加速度基本呈对称状态。主梁跨中位移和加速度的整体变化趋势表明，车辆影响了斜拉桥的局部动力响应。

（3）桥梁跨中竖向位移、加速度及冲击系数随着车速的增加有增大趋势，但并不是一直无限制增大。