微球聚焦测井仪推靠系统多目标优化设计

任 涛 ，冯 斌，孙 文，张春琳，唐道临

1.西安石油大学机械工程学院，陕西 西安 710065；2.成都北方石油勘探开发技术有限公司，四川 成都 610051；3.延长油田股份有限公司物资装备部，陕西 延安716000

引言

微球聚焦测井仪是石油测井领域内一种十分重要的测井设备[1]。现有的部分测井设备存在工作效率低下、设备机械运行可靠性低、稳定性差、执行机构不能准确到位等缺陷，并且设备的运营故障及维修成本高昂等问题，因此，需要对测井设备的设计提出新的设计要求[2]。本文在微球聚焦测井仪推靠系统的设计过程中引入多目标优化设计方法来改善上述问题。调研发现，大量学者在这方面进行了研究，邢家乐等应用Adams 运动仿真平台，对新型VSP 仪器推靠机构进行了仿真与优化[3]；赵斌等[4-5]进行了基于Matlab 推靠系统参数优化研究；赵宏林等对过套管电阻率测井仪推靠系统机构优化进行研究[6]；沈迪成等进行了推靠系统的整体结构优化研究[7]。文献[8-9]主要借助Matlab 与Adams仿真平台，针对不同工况对关键部件进行了仿真优化分析，但是受限于时代背景，没有建立准确的优化数学模型，对于各种约束条件也未作全面考虑；或仅考虑局部变量的单目标优化，未进行系统性分析，具有较大的局限性。

在众多学者的研究基础上，针对推靠系统在实际测井作业过程中机构运动到位但推靠力不足的问题，以推靠系统运动及动力特性分析为基础[10]，从微球聚焦测井仪推靠系统的完整性出发，提出基于推靠系统传动角优化目标以及以推靠极板质心点速度[11-13]、加速度为优化目标[14-15]的多目标优化方法[16-17]，建立推靠系统多目标数值优化设计模型。并应用全新的改进复合形-遗传算法来求解该优化模型，改进的复合形算法是基于原有复合形算法框架的基础上引入了遗传算法在解决多目标优化问题上的诸多优势[18]：增加了初始化种群的随机性，扩散了初始化的搜索区域，集群化搜索策略将局部最优解扩展为全局最优解；群体间以及个体之间的信息交换、变异等交叉策略；丰富了搜索对象，进而加速寻优过程，更高效地找出全局最优解[19]。

1 微球聚焦测井仪推靠系统运动分析

图1 为微球聚焦测井仪推靠系统的机构运动简图。原设计中的柱销滑槽副，这里用滑块-滑槽代替。通过文献[8]测井仪推靠系统机构动力特性分析与研究，得出测井仪推靠极板运动方程[21-22]

图1 微球聚焦测井仪推靠系统单臂机构运动简图Fig.1 Motion diagram of single arm mechanism of push system with microsphere focusing logging tool

1.1 推靠极板上约束圆柱销B 质心点位移方程

根据推靠系统单臂机构运动简图及运动学定理可得推靠极板上圆柱销B质心点的位移方程为

1.2 推靠极板上约束圆柱销B 质心点速度方程

通过对式（1）两端求导可得推靠极板上约束圆柱销B质心点的速度方程为

1.3 推靠极板上约束圆柱销B 质心点加速度方程

通过对式（2）两端求导可得推靠极板上约束圆柱销B质心点的加速度方程为

1.4 微球聚焦测井仪推靠系统工作行程传动角

推靠系统传动机构在井下的工作行程并不是整周期运动，而是在一个工作行程中，推靠臂张开带动推靠极板运动，使得安置于推靠极板上的微球极板贴合井臂。因此，在推靠系统的工作行程中的传动角区别于传统的整周期传动角分析，不存在理论上的极限位置角。为改善推靠系统的传动性能，保证推靠极板的推靠力，即保证推靠极板与井壁的贴合程度，为微球极板的数据采集提供保障。

因此，对推靠系统在工作行程的传动角进行分析[11-12]。根据图1 微球聚焦测井仪推靠系统单臂机构运动简图以及上述角度关系，可得传动角

2 多目标优化设计数学模型

2.1 设计变量

根据机构运动简图，以机构尺寸的各杆长度、推靠内壁的固定铰接点位置坐标、推靠上臂的固定铰接点距推靠内臂固定铰接点的竖直距离、推靠内臂的结构弯折角、滑块E的起始位置坐标以及两个滑块在推靠极板以及推靠主体上的行程空间等为设计变量，即

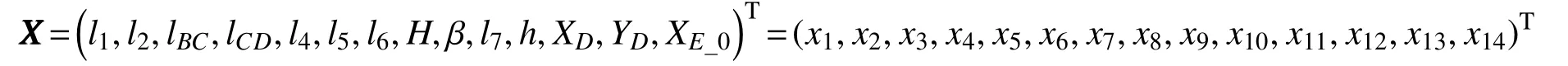
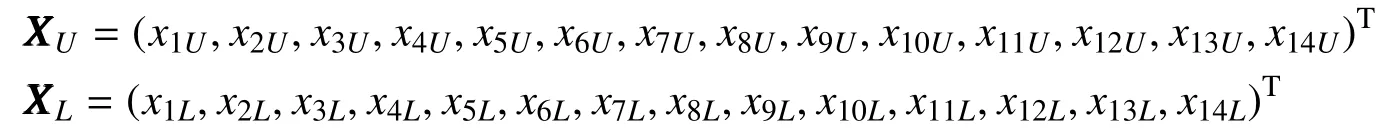
2.2 目标函数及其处理过程

综合该测井仪推靠系统主传动机构时，工程人员期望该推靠系统具有良好的运动平稳性，要求推靠极板的速度波动平稳，加速度跳动量较小，并且具备良好的传力性能，以方便微球极板贴靠井壁测量数据。

通过对推靠系统的运动分析，获取实际工况条件下的期望速度、期望加速度以及期望传动角作为目标函数中的评价指标。根据工程需求，提出如下目标函数。

（1）目标函数f1(X)：推靠极板铰接处滑块在行程内的滑移速度围绕期望速度平稳波动。

（2）目标函数f2(X)：推靠极板铰接处滑块在行程内的滑移加速度波动最小，希望滑块在工艺阶段加速度波动平稳。

式中：

（3）目标函数f3(X)：工作行程内的最小传动角大于等于期望传动角；从而保证传动角在理想范围内，具有理想的传动能力。

式中：γ0测井推靠系统的期望传动角，一般取γ0=40°；

γj(X)测井推靠系统的实际传动角，（°）。

由于各目标函数的单位是各自不同的，为分析方便，建立统一的分析机制，因此，首先要对各目标函数作归一化处理[23]。

总目标函数采用多目标函数最优化方法中的统一目标法对分目标函数进行直接加权，在进行直接加权时，分目标函数的变化范围为[9]

式中：αi，βi目标函数变化值的上下限。

指标的容限

指标的加权因子

设计变量的加权参数见表1。

表1 设计变量的加权参数Tab.1 Weighted parameters of design variables

根据已知目标函数的变动范围以及目标函数的优化重要程度，计算（或估计）出加权因子，现建立总目标函数如下

2.3 推靠系统工程化约束条件

由于测井仪推靠系统井下工况的特殊性，对其进行工程优化需要综合考虑机构成立约束条件，机构高度，运动约束等性能指标。现建立推靠系统工程优化约束条件如下[17，20]。

（1）为保证机构能够正确运行，根据Grashof 准则，可得Grashof 双曲柄机构杆长约束条件为

（2）滑块行程H应满足设计公差要求，建立不等式约束条件为

式中：

Hmin允许的滑块行程最小值，一般取Hmin为滑块理论设计行程；

Hmax允许的滑块行程最大值，一般取Hmax=1.5Hmin。

（3）为保证推靠内臂BCD的可制造性和装配性，需对其夹角β 进行约束

2.4 优化算法

复合形-遗传算法是一种集合复合形算法以及遗传算法各自优点的新搜索算法[18-19]。它是针对复合形算法在处理设计变量较多或者目标函数较为复杂的优化问题时，出现的易于局部收敛而无法全局检索，即无法保证最终的优化结果是全局收敛的最优解而提出的改进算法，改进的复合形算法是基于原有复合形算法框架的基础上引入了遗传算法在解决多目标优化问题上的两大优势：群体搜索策略和群体间个体之间的信息交换；使得改进的复合形算法在求解多目标优化问题上更加高效。具体改进如下。

（1）利用遗传算法的随机性，在随机生成可行点时增加初始可行点的随机性。

（2）在求最坏点的映射点时，采用向最好点映射的方法，充分利用优点信息。

式中：

x(R)——映射点；

x(L),x(H)——复合形各顶点中的最好点，最坏点；

κ—映射系数，一般初始κ＞1，同时具有自适应性。

（3）借用遗传算法的思想，对每次进行新的复合形顶点形成过程进行一次变异，即对形成复合形的各顶点进行可行化变异

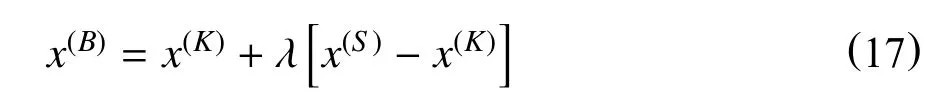
式中：x(B)变异点；

x(S)除去最坏点之后各顶点的几何中心点；

λ—具有自适应性的变异系数；

x(K)复合形的各顶点，变异后的各可行变异点构成新的复合形。

改进后新的复合形算法在寻优过程中，相较于标准复合形而言，具有以下优点：（1）改善了最优解空间的局限性，扩大了复合形顶点在可行解空间中的范围，从而增大了搜索最优解的范围，避免了出现局部最优解；（2）在最坏点映射时，用最好点代替中心点，让最坏点向最好点映射，加快了优化计算的收敛速度。

图2 为应用改进复合形算法的微球测井仪推靠系统机构优化设计流程图。

图2 改进复合形推靠系统机构优化算法流程图Fig.2 Flowchart of optimization algorithm for improved composite push system

3 优化结果与讨论

3.1 算法参数设置与优化结果

以正在研发的微球聚焦测井仪推靠系统主传动机构为例，考虑实际工况，根据推靠系统工作机构的工艺要求以及推靠系统的运动学分析，建立推靠系统主传动机构优化设计模型[20]，对推靠系统主传动机构几何参数、运动参数以及传动压力角进行多目标综合优化[14-15]。

现设定设计变量个数N=14，根据现有的推靠系统的机构尺寸参数，对设计变量初始值选择如下：xxx0=(280,294,315,76,375,88,80,65,170π/180,313,37,80,−37,233)T；并设置设计变量X的上下限XU，XL取值如下：XL=(260,285,310,50,370,80,75,60,120π/180,300,30,60,−40,220)T；XU=(290,320,330,80,410,90,95,75,170π/180,320,42,85,−30,240)T；另外，已知该推靠系统主传动机构的主要技术参数：测井推靠系统的期望传动角γ0=40°；推靠上臂的初始角速度ω0=3°/s；目标井径参数DO=25.4 mm×8.5 mm；圆柱销B距离铰接点A处的初始距离s1−0=190 mm；滑块E距离铰接点D处的初始距离s2−0=153 mm。

通过复合形-遗传算法对微球聚焦测井仪推靠系统的主传动机构进行优化，优化结果见表2。

表2 微球聚焦测井仪推靠系统主传动机构优化设计结果Tab.2 Optimal design results of the main drive mechanism of the push system of the microsphere focusing logging tool

3.2 比较分析

从表2 中可以看出，为验证文中所建立的基于测井仪推靠极板质心点的速度、加速度以及测井仪推靠系统主传动机构工作行程内的传动角为优化目标的微球聚焦测井仪推靠系统主传动机构的优化模型的正确性，将优化设计过程分为了两大类分属4 种结果，前3 种情况分别以各自目标函数f1(X)、f2(X)及f3(X)为单目标进行优化。即单独以测井仪推靠极板质心点的速度、加速度以及测井仪推靠系统主传动机构工作行程内的传动角为独立目标进行优化，第4 种情况为综合考虑所有目标函数经加权处理后，以总目标函数F(X)为最优解函数进行多目标优化。4 种情况经分析计算发现，各目标函数都接近于零却又无法达到零。经分析后发现，这与所取的推靠系统的各期望参数有关，除此之外，还与所取的离散点数有关，为提高运算效率，选取了200 组样点数。综合分析，其计算结果满足设计要求。

图3、图4 和图5 分别为4 种优化后推靠极板质心点速度、加速度以及推靠系统主传动机构在传动过程中的传动角曲线与原设计条件下的曲线结果的比较。

从图3 中可以直观地看出，单独以f1(X)为优化目标时，可以获得最为稳定的速度波动，但是速度曲线的峰值较低，在测井仪器工作过程中需要推靠系统具有较快的响应速度，平稳的贴靠过程。该优化结果不足以满足测井仪器的工作需求。观察图3中的优化结果可以发现，单独以f2(X)为目标函数的优化结果同样如此，整体速度波动平稳，但是速度峰值较低。以f3(X) 作为单独目标函数进行优化，可以发现优化结果在维持原有速度轨迹的基础之上，降低了速度峰值，改善了速度波动冲击，并使速度峰值维稳在一个小区间内。以综合目标函数F(X)进行的多目标优化结果，在推靠系统启动与结束时间段速度波动平稳，而在稳定工作段速度稳步上升，但是从整体来看，速度较低不利于实现推靠系统的快速张开过程。通过对比分析，发现独立以传动角均方根函数f3(X)作为单独目标函数的优化结果能够较好地满足推靠系统快速响应，尽快贴靠井壁的工作需求。

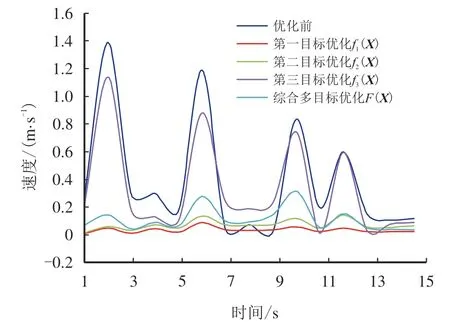
图3 推靠极板质心点速度曲线优化前后比较Fig.3 Comparison before and after optimization of velocity curve of centroid point of polar plate

图4 推靠极板质心点加速度曲线优化前后比较Fig.4 Comparison of acceleration curves before and after optimization of pushing center plates

从图4 可以看出，分析结果基本与图3 相似。单独以f1(X)、f2(X)为优化目标时，推靠极板的质心加速度最为稳定，但是加速度曲线的峰值过低，在测井仪器工作过程中需要推靠系统快速响应，尽快地贴靠井壁，而以此目标函数条件下的优化结果难以满足工作需求。以f3(X)作为单独目标函数的优化结果，同图3 结果类似，优化后的加速度曲线改善了初始加速度的冲击，降低了加速度峰值，减小了加速度的峰值波动，并保持有恰当的加速度，维持优化前的加速度轨迹形态，可以较好地满足油田测井的实际作业要求。以综合目标函数F(X)进行的多目标优化结果，在推靠系统启动与结束时间段加速度接近于零，在稳定工作段加速度峰值有所提升，单纯从加速度冲击来说，该优化结果得到了较大的改善，但从满足测井推靠系统快速响应，尽快贴靠井壁的工作需求来说，不能满足实际的作业要求。

图5 推靠系统传动过程中主传动机构传动角曲线优化前后比较Fig.5 Comparison of transmission angle curve of main drive mechanism before and after optimization in driving process of pushback system

从图5 可以看出，单独以f1(X)为优化目标时，由于目标函数f1(X)是以推靠极板质心点速度为目标函数，因此，以其作为优化目标对推靠系统主传动机构的传动角基本没有影响，因推靠系统主传动机构在传动过程中的传动角依然维持原样。而以加速度f2(X)为单独优化目标时，由于极板加速度与主传动机构传动角的关系，使得主传动机构的传动角轨迹与原设计呈相反趋势变化。

单独以f3(X)作为优化目标时，由于f3(X)本身就是以传动角作为目标，因此，优化后的结果使得整个机构在工作过程的传动角整体增大，维持原有的变化趋势。将f3(X)的优化结果折算可知，单独以传动角为优化目标时，极板推靠力可达238.6 N，相较于原本的211.9 N，极板推靠力提升了12.6%，满足油田的实际作业要求。

而以综合目标函数F(X)进行的多目标优化结果，可以看出，在推靠系统贴靠井壁的过程中，主传动机构的传动角以对称方式体现，在启动和贴靠过程具有较大的传动角，中间过程中传动角略有下降，但考虑到在极板贴靠井壁后的传动角低于以目标函数f3(X)的优化结果。即综合多目标优化结果，在极板推靠力上，无法达到既定的目标要求，低于238.6 N，于优化前的最终极板推靠力基本保持一致。

综合对比分析发现，综合目标函数优化结果在机构运动平稳性方面有较大改善，并且在推靠系统的启动过程实现了较大的初始传动传动角。但是结合实际考虑，极板推靠力优化结果无法满足极板推靠力的预定要求。在油田实际测井工程应用中，首先要保障极板推靠力达到预期，这样才能保证测井作业数据的有效性与准确性。

因此，综合考虑各优化结果，发现单独以目标函数f3(X)进行优化求解，能够满足实际测井的作业要求，保障极板推靠力接近240 N，并且其在机构运动的速度，加速度峰值波动方面有所改善，缓解了机构运动过程中的杆件冲击，改善了机构运动的平稳性。综上所述，以目标函数f3(X)，进行的多目标优化结果满足系统的期望优化结果。

4 结论

（1）提出了基于推靠极板速度、加速度以及推靠系统主传动机构工作行程内的传动角为优化目标设计要求的推靠系统的优化设计方法。

（2）基于微球聚焦测井仪推靠系统主传动机构运动学分析基础，以及微球聚焦测井仪推靠系统的实际工程化设计约束条件，建立了以测井仪推靠极板质心点的速度、加速度以及测井仪推靠系统主传动机构工作行程内的传动角为优化目标的微球聚焦测井仪推靠系统主传动机构的多目标优化设计模型。

（3）根据该优化设计模型，应用改进的复合形算法，快速地计算出机构参数合理并且满足众多目标函数的理想推靠系统机构。为测井仪推靠系统主传动机构的实际应用提供多组备选方案。

（4）将优化结果与原设计的微球聚焦测井仪推靠系统进行动力性能分析比对，优化后的推靠系统在运动平稳性以及推靠极板的传力性能上有较大的改善，验证了其优化方法的正确性与有效性。其研究方法和研究成果具有一定的参考意义。