风力发电机的高精密风速检测系统设计

李研达，薛 琦

(1.安阳师范学院物理与电气工程学院，河南安阳 455000；2.郑州大学信息工程学院，河南郑州 450001)

0 引言

在风力发电机的风速风向检测方面以机械式为主，传送带和压力传感器相结合的方式，皮带长时间使用后会磨损[1]，压力传感器在低风速下薄膜振动很小,精度非常差，检测量程受限；精密风速检测系统以多普勒为原理，但原理复杂、造价昂贵且环境适应性差[2]；超声波技术原理简单,技术可靠，无需机械配合部件，与现在信号处理方法结合后同样也可以达到较高精度。本文采用超声波检测原理和时差计算程序设计了高精密风速检测系统。

1 超声波风速检测原理

超声波风速检测原理如图1所示。在两维空间中，按照360°空间均匀分布8个超声波传感器，超声波的传播途径受风速影响，8个传感器采集的风速转换成向量[3]，最后合成一个风速矢量v，风速受温度、气压等影响因素不在考虑范围。

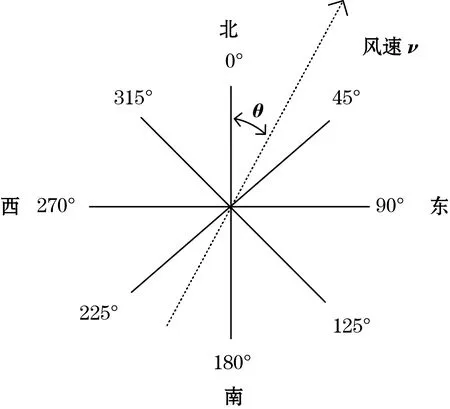
图1 风速检测原理

将东西两个相对方向的速度、时间、距离建立风速检测模型：

(1)

同理，以相同的原理建立南北方向的模型：

(2)

式中：v为风速；θ为风速与不同方向的传感器之间的角度；t1和t2分别为能量发射后东西方向接收顺逆风信号的时间；t3和t4分别为能量发射后南北方向接收顺逆风信号的时间。

本系统8个角度中，以东南西北4个方向的计算结果作为基准，其余4个方向计算出的结果用于校准风速。联立式(1)和式(2)求解出风速和角度。

2 高精密风速检测的硬件系统

按照功能需要设计硬件模块，DSP主控模块用于检测采集数据和计算，驱动电路为超声波传感器提供能量[4]，ADC数据采集电路用来保证系统采集数据的有效性。

2.1 风速检测硬件总体系统架构

由于风速检测硬件安装在风力发电机上方，因此对硬件稳定性、环境适应性等都有较高要求，硬件系统架构如图2所示。主控模块作为超声波检测系统的核心，需要保证与上位机通讯的同时，同步产生8路高速方波激励脉冲信号，模块占空比等参数可调[5]。在主控模块采集到超声波信号后计算风速，发射通道和驱动电路产生PWM脉冲信号，最后以超声波传感器稳定输出信号为主，高速数据采集电路包括调理电路和ADC通道[6]，调理电路为量程可调，ADC通道有16位数据地址，50 μV的分辨率满足系统要求。

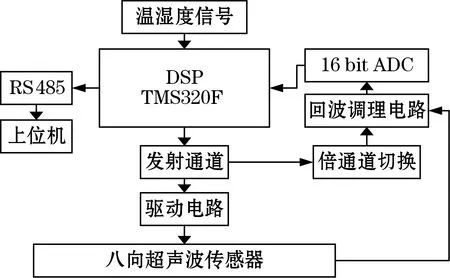
图2 风速检测硬件系统

2.2 方波驱动电路

传感器产生超声波时需要实现机械能和超声波之间的转换，核心处理电路在引脚HIN和LIN上产生200 kHz方波，最后将激励信号转化为超声波能量，设计电路如图3所示。IR2110是一种专用的高速脉冲芯片，芯片电源采用+5 V电源，并连接两个电容滤除高低频率的电源噪声[7]，输出部分连接到2个MOS管，输出信号和MOS管之间的匹配电阻为100 Ω，输出信号同时连接10 μF和0.1 μF滤波电容，2个MOS管组成半桥电路并由OUT输出激励脉冲信号。

图3 方波驱动电路

由于方波脉冲频率为200 kHz，选择合适的栅极电阻R493和R494对于驱动MOS来说非常重要。栅极电阻值太小会造成栅极驱动电压过冲，导致开关管过快导通。同样，电阻值过大会导致过阻尼，并延长开关管的开通时间，因此，过小或过大的栅极电阻都会影响栅极驱动的效果。合适的栅极电阻应该使驱动电路的品质因数(Q值)在0.5(过阻尼)～1(临界阻尼)之间。一般可以选择Q值为0.55即可，这样可以快速打开和关闭器件，也不会产生有害的谐振。驱动后的频率上下管的驱动会相互导通，信号Sign+和Sign-的具体波形如图4所示。

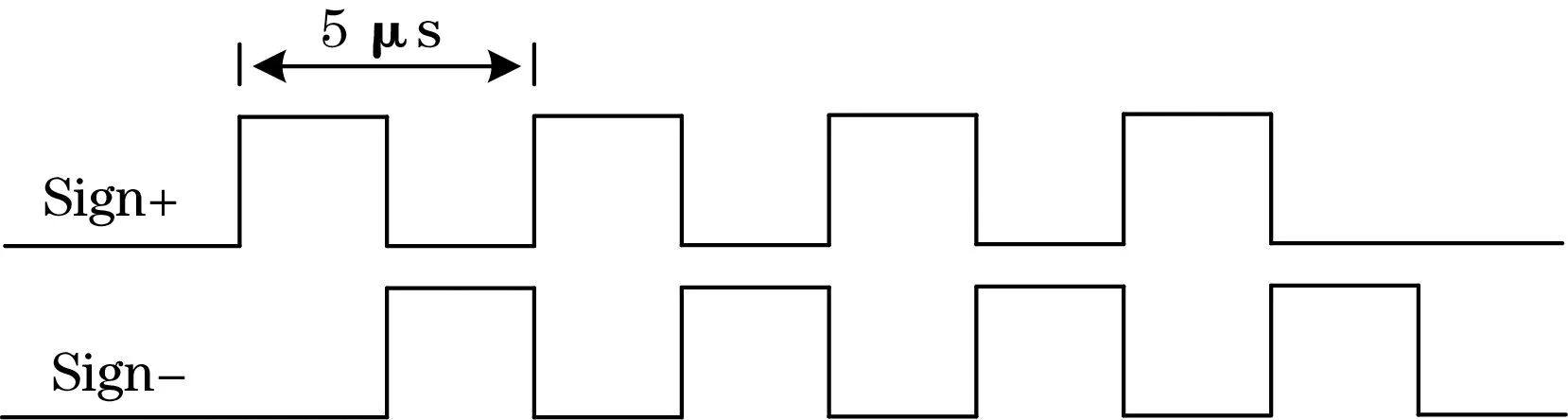
图4 驱动信号的PWM波

2.3 高速数据采集电路

发射驱动电路产生的超声波信号中含有高频噪声，高速数据采集电路需要对微弱信号进行滤波放大，再将输出传输到核心处理模块中[8]，具体电路设计如图5所示，核心放大器TLC6752的频率为80 MHz，逐次逼近型ADC驱动放大器的功耗为7 mW、采样速率为100 KB/s，输入信号VIN+引脚连接49.9 Ω的匹配电阻[9]，放大器采用负反馈放大功能增加稳定性，信号经过ADC数据采集后经由SPI数据总线传输到核心处理模块中。

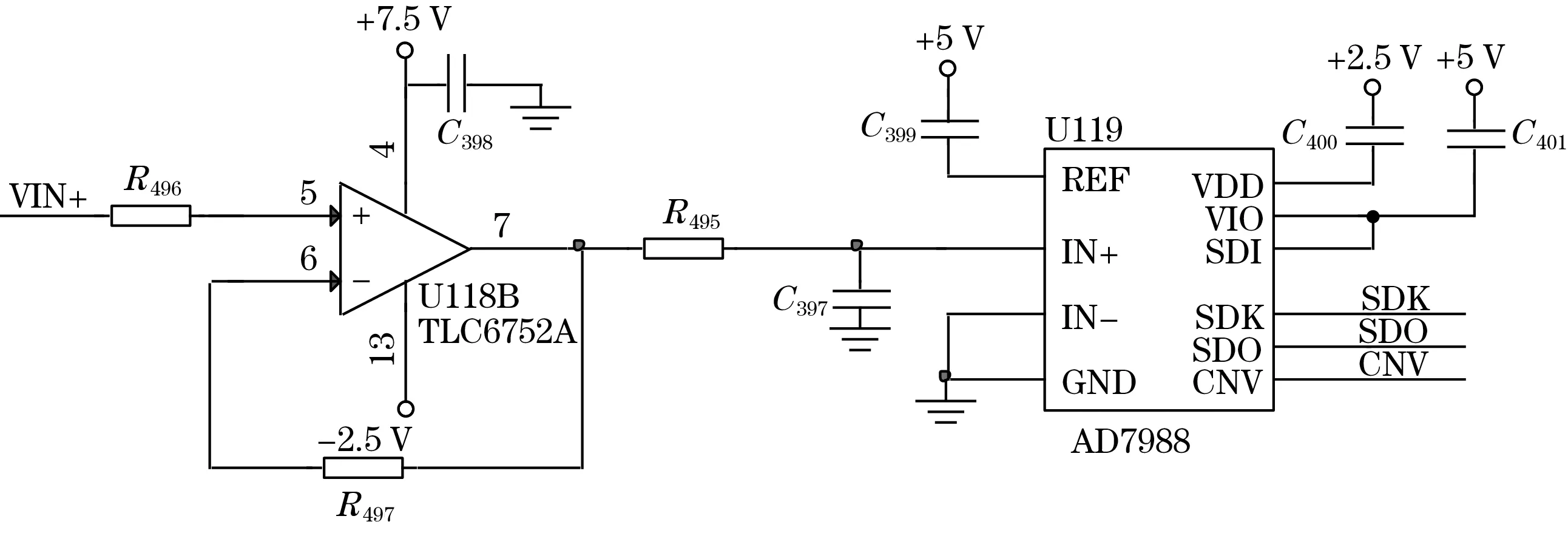
图5 高速数据采集电路

在高速数据采集仪的前端设计一个放大电路，通常采用差分放大电路，由于其具有抗共模噪声能力强，失真小，信号建立通道时间短等优点。单通道运算放大器电路的参数最重要的是压摆率，这与输入信号及芯片带宽等都有关系，简化后的计算公式为

SR=2πfmaxA/106

(3)

式中：SR为差分放大电路的压摆率；fmax为最大输入脉冲频率，fmax=200 kHz；A为最大输入电压幅值。

根据式(3)计算出差分放大电路的参数，统计整理如表1所示。

3 高精密风速检测的软件系统

高精密风速检测系统的硬件可以保证信号的稳定性，计算风速下超声波的时差和风向风速等参数时，需要使用核心处理器的程序对数据计算处理。

3.1 时差提取程序

采用时差提取程序获得振荡信号的特征，具体提取算法如图6所示，首先，硬件系统开始接收信号，超声波正弦信号经过传播后变为调制振荡信号，从振荡信号中提取每2个波峰之间的差值，以最大波峰信号为特征波[10]，根据2个特征波周期得出传播时间和距离，重复测量3组数据后确定有效时差特征，最后将提取的信号转化为风速。

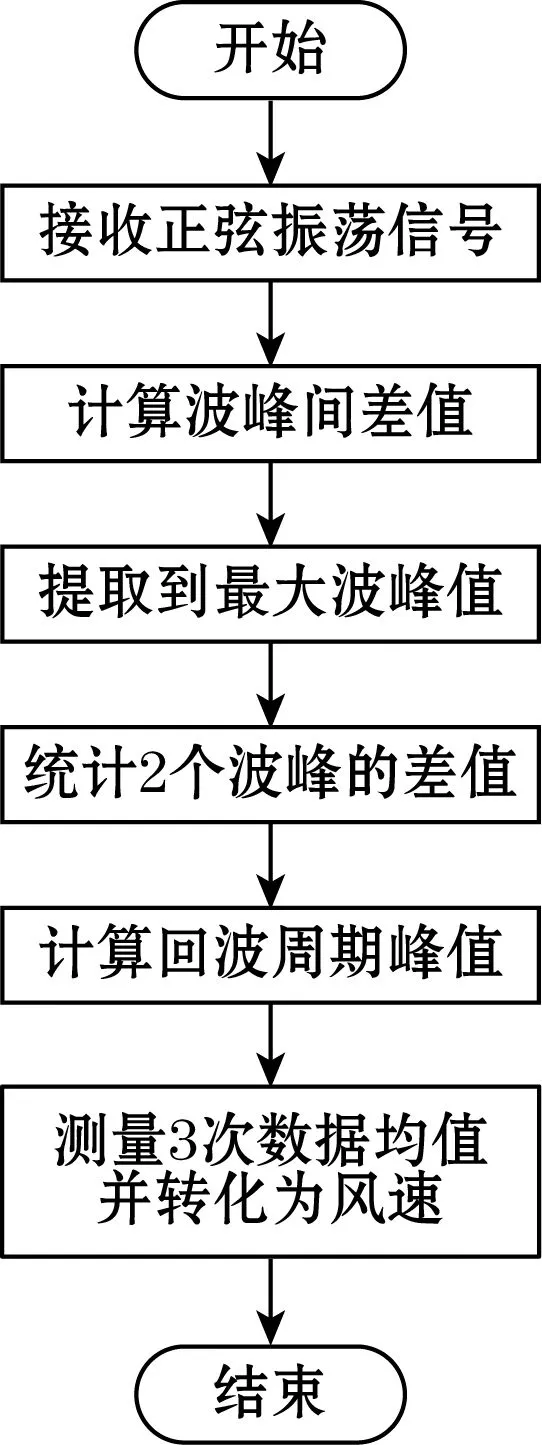
图6 时差提取程序

设置相同的检测距离，根据振荡信号的波峰数值提取出前14次的振荡波峰，结果见表2。

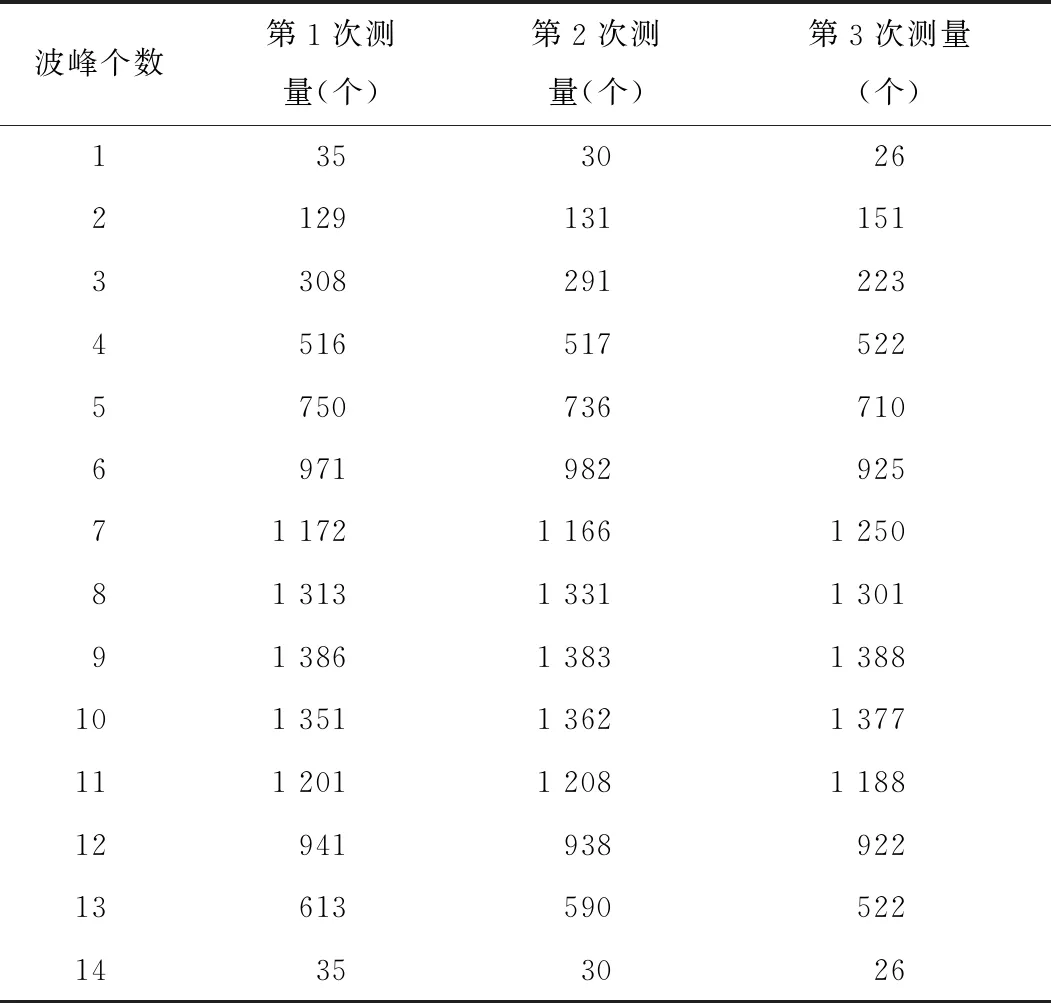
表2 多次波峰数值

得到波峰数值后利用线性拟合的方法计算出每个脉冲过零点时的数值，具体求解过程如图7所示，相邻2个波峰和波谷分别为A1和A2，根据2个点的坐标得出直线的斜率为A1/(A1-A2),图例中过零点为1.8 ms，零点时间加上硬件采用时间即为超声传播时间，同样的原理计算出其余数值。

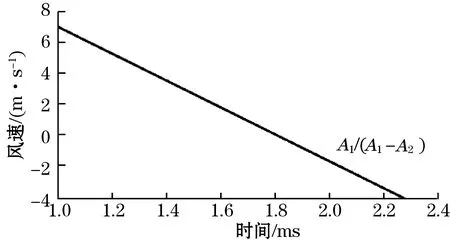
图7 线性补偿计算过零点图

根据传播时间和速度就可以得出合成风速，合成风速的具体原理见图8，利用拟合后的风速和实际风速对比如表3所示，从拟合结果可以看出拟合的有效值与实际数据相差不大，即风速基线基本一致，但拟合后的结果数据波动更小，因此还需要乘以一定的系数校准拟合数据更好。

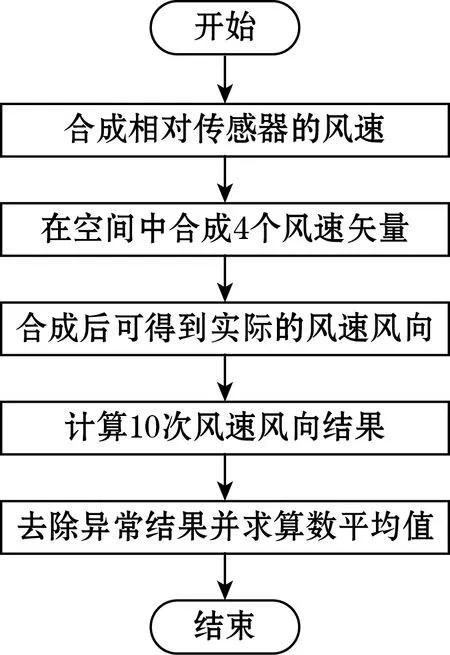
图8 风向向量合成程序

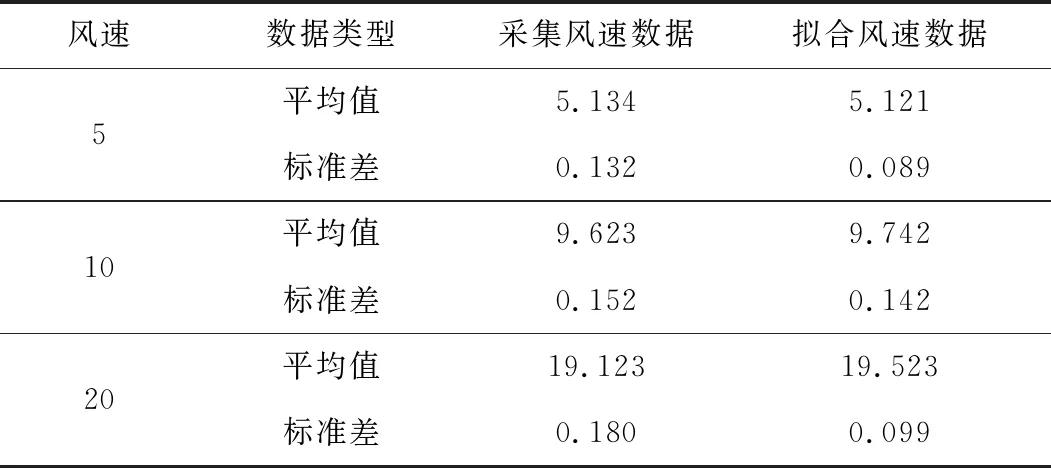
表3 拟合风速结果 m/s

3.2 风向向量合成程序

在风向向量合成程序中，共有8个超声波通道接收信号，其中每2个平行向量为一组信号，具体风向向量合成程序如图8所示。在合成传感器的相对风速时，逆风状态下计算出2个合成向量为负[11]，顺风状态下为正，在二维空间中将4个风速矢量合成，最后得到的向量表示为最终风向风速，合成向量长度即为实际风速，合成向量角度与风速角度一致，10次测量后求出算数平均值即可。

3.3 风向角度修正

在判断风速检测方向时，由于东南西北4条通道合成后的结果存在的误差比较大，经过另外4条通道校准后可以修正到检测数据与风速合成保持一致，但由于螺纹等结构配合问题，通过优化算法程序是不能修正的，因此必须通过实际测量完成修正。螺纹安装配合公差原理见图9，螺纹宽度为14 mm，高度为1.4 mm，按照标准加工时会存在±0.15 mm的制造公差，因此计算出角度偏差α约为±0.8°，此数值必须人为修正风向计算程序。

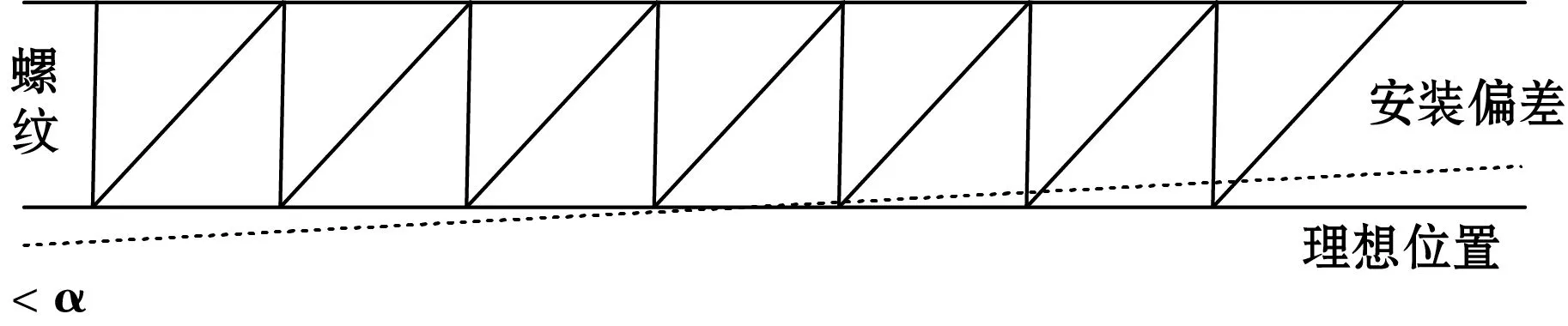
图9 螺纹安装配合公差

4 高精密风速检测的试验验证

为验证高精密风速检测系统的可靠性，从硬件功能和系统功能分别验证，硬件功能采集超声波回波信号验证，系统功能采用搭建风速环境验证风速和风向的精度。

4.1 超声波采集信号

超声波回波信号是方波驱动模块发出后再读取进检测系统的信号，具体采集结果如图10所示。微弱的电路噪声等并不会影响回波波形，波形在第5个波峰达到极大值并作为特征波[12]，特征波后振荡开始衰减，这跟风速不稳定有关。

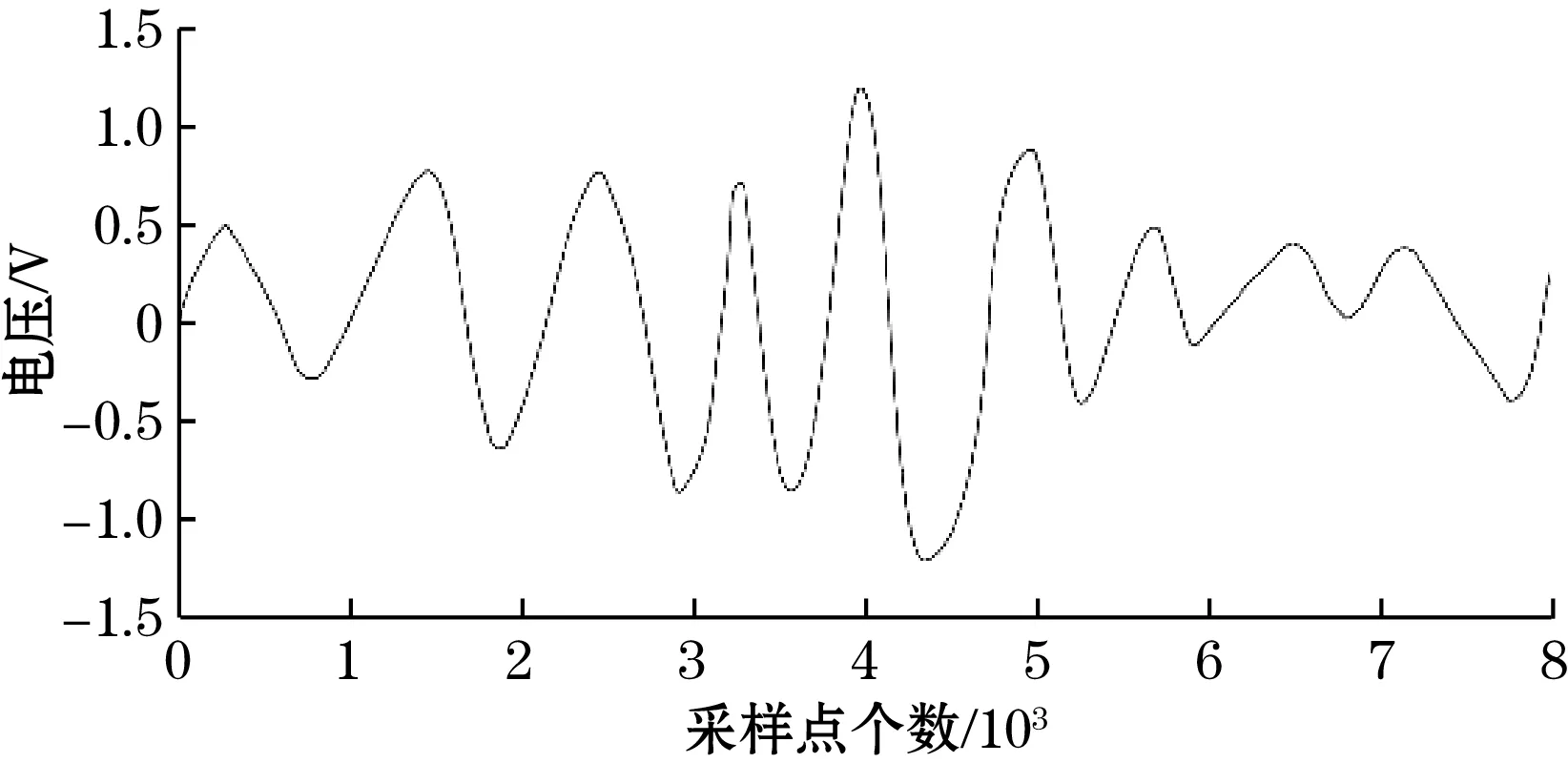
图10 回波信号波形

为验证系统检测风速的精度，在密闭环境中测量静态下流动空气的风速，采集风速和拟合的平均风速见图11，对测量数据求平均值、标准差等统计在表4中，经过3次数据显示，风速的平均值最低能达到0.016 m/s，因此测量分辨率至少在0.01 m/s，最大标准差为0.011 m/s，证明系统运行稳定，测量数据的偏离误差很小，因此仪器对风速检测可以满足高精度的要求。

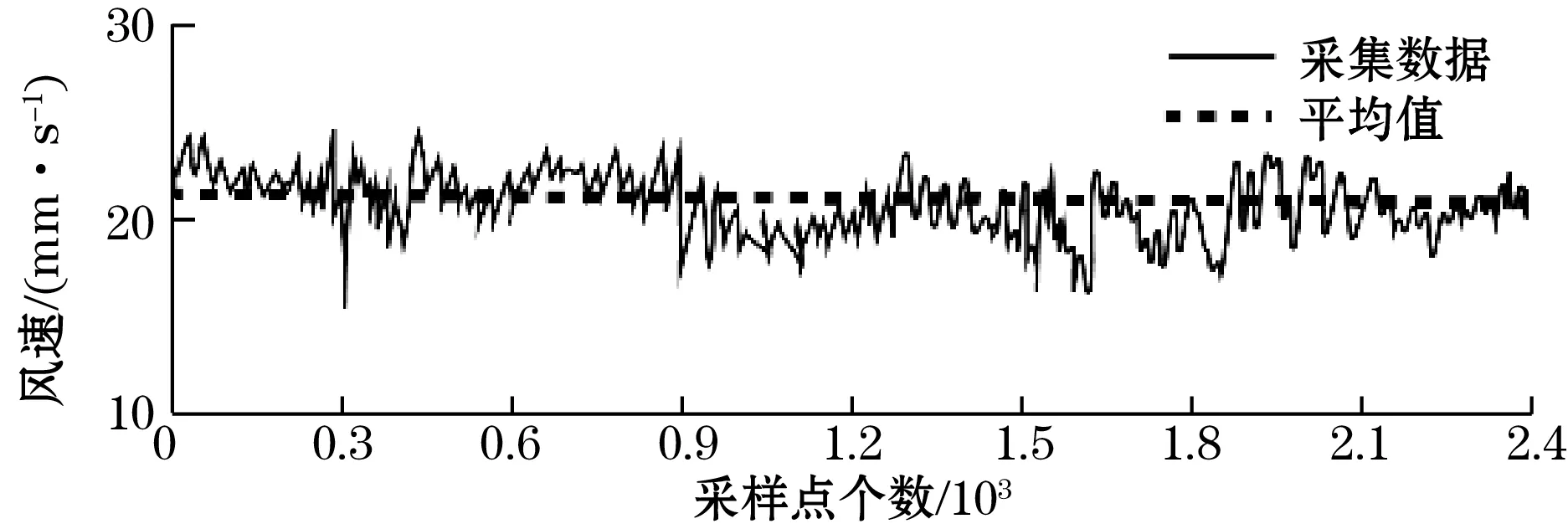
图11 拟合效果图

4.2 风扇风速测量

搭建风速试验环境，用风扇测试风速检测系统，

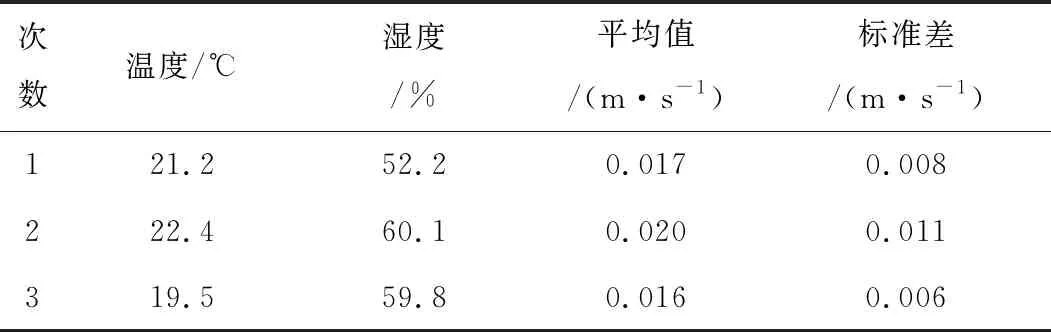
表4 零风速验证结果统计

分别验证风速和风向，测试风速时分别以低、中档吹向检测系统，如图12所示。风速检测结果具体见图13，在风扇关闭时密闭环境存在自然风，系统显示为0.2 m/s的风速状态，另外2个档位分别稳定在1.7 m/s和2.4 m/s，风速精度可以达到0.1 m/s。

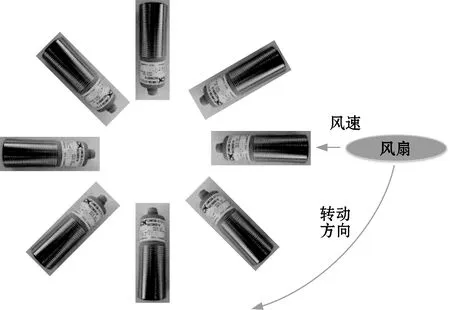
图12 测试方案简图

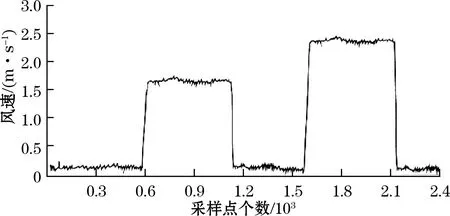
图13 风速信号波形

旋转风扇测试风向，用中档风吹向高精密风速检测系统并旋转0°～120°，具体结果见图14，在旋转过程中由于手持操作造成风向不稳定的状态，在60°和120°两种角度下短暂停留一段时间，转动圈数范围内角度误差可以控制在5°内，系统启动和响应速度都可以满足要求。

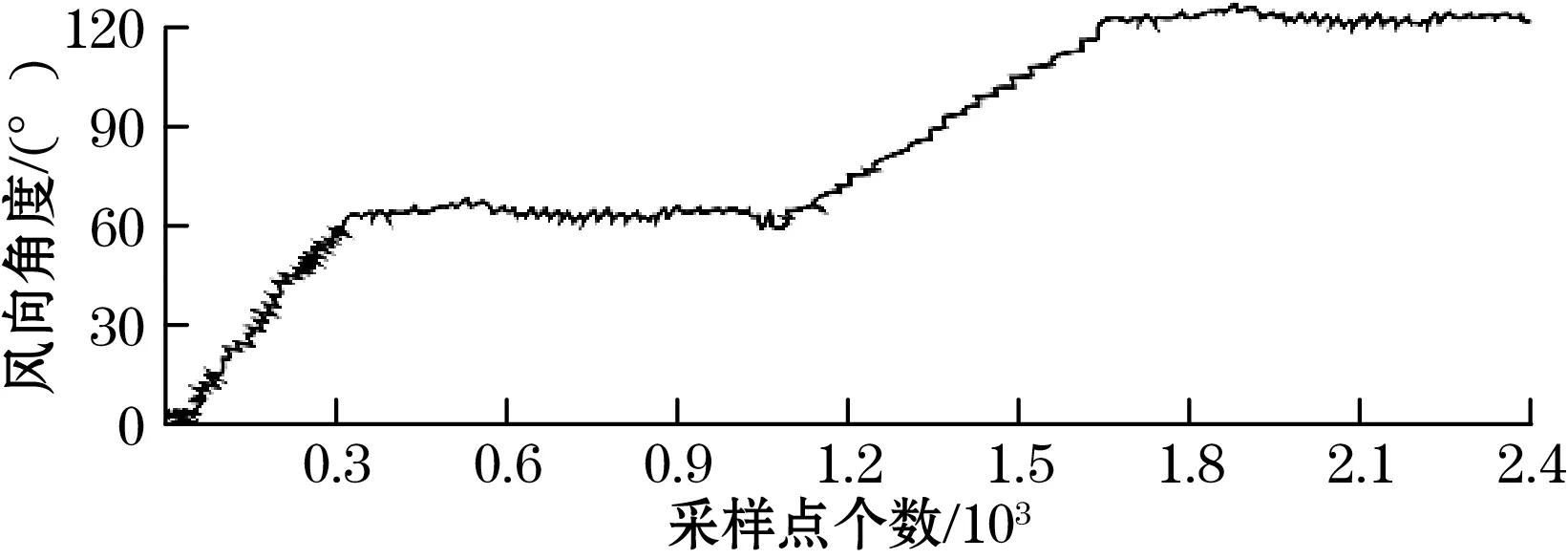
图14 风向信号波形

5 结束语

本文采用超声波原理设计了风力发电机高精密风速检测系统，首先分析风速检测原理，然后对风速检测硬件系统、发送200 kHz方波的驱动模块和16位高精度数据采集模块进行设计，设计时差提取程序判断风速，风向向量合成程序计算风向，搭建基于风扇的风速风向试验平台。分析结果显示，在不同风速风向模式下，风速测量精度为0.1 m/s，风向精度为5°。