非线性压电俘能技术研究现状及趋势分析

陈孝玉，张旭辉，左 萌，汪 林，佘 晓，陈路阳

(1.西安科技大学机械工程学院；陕西西安 710054；2.遵义师范学院工学院，贵州遵义 563006； 3.陕西省煤矿机电设备智能检测与健康维护重点实验室，陕西西安 710054)

0 引言

能源问题已成为全世界共同关注的问题，各国科技者都在致力于发展新型能源以及克服传统能源所带来的问题。当前无线传感网络节点大多采用电缆或电池供电，电缆供电布线复杂，需要电源有线连接，严重影响无线传感技术的应用；化学电池电能输出稳定，但其能量容积有限，需要定期维护或者更换，频繁更换或者维护电池不仅增加使用成本，而且在一些特殊场合的应用变得极为不便甚至难以触及，如野外监测、人体内、深海等无线传感器的应用。同时，化学电池废弃对环境构成严重的污染也是亟待解决的问题。考虑到无线传感器等电子产品功耗较低，可以通过俘获外界能量以为其提供电能实现自供电。环境中的能量包括：太阳能、温差能、噪声和振动等，太阳能和温差能受天气条件的影响大，难以满足微电子产品稳定供电的需求，而振动和噪声广泛存在于环境中且不受气候条件的影响。将振动能量转化为电能有压电式、电磁式、静电式等转换方式[1]。相对而言，压电式转换方式具有能量密度高、结构简单、易于和微电子产品结合等优点[2]。

在早期的压电能量转换技术研究中，研究者多集中在单自由度的线性压电俘能器，线性压电俘能器有效工作频带很窄，一旦外界频率偏离其固有频率后，电能输出会急剧下降[3]。这显著限制了压电俘能器的应用，如何拓宽压电俘能器的有效工作频带被关注。比较而言，非线性压电俘能器在不牺牲能量密度条件下，可以在大的、连续的频带实现电能输出，有效提高俘能效率[4]。成当前压电俘能技术研究的重点，代表了压电俘能系统研究的发展方向[5]。本文对近几年非线性压电俘能器的研究进行了综述，主要内容包括非线性压电俘能器工作原理，不同原理的非线性压电俘能器以及相应特性等，最后对非线性压电俘能技术发展趋势进行了分析与总结。

1 非线性压电俘能器简介

压电俘能器工作原理是基于压电材料的正压电效应，将振动能量转化为电能输出，对于非线性压电俘能器而言，其振动俘能过程是非线性振动过程，非线性振动能拓宽俘能器工作频带，使其在较宽频带范围产生有效电能输出。

1.1 非线性振动宽频机理

非线性振动能量采集振荡器的运动方程可表示为[6]

(1)

式中：x为振动位移；γ为阻尼系数；f(x)为外界激励；U(x)为系统势函数。

多数非线性振动能量采集振荡器可以用Duffing振荡器表示，故其势函数U(X)由式(2)确定：

(2)

式中a、b均为常数。

将式(2)带入式(1)即可得非线性振动微分方程：

(3)

其振动频率-位移响应曲线如图1所示[7]。

图1 振动频率-位移响应曲线

由图1中可以看出，当b>0时，频率-位移响应曲线向左弯曲，称为软弹簧特性非线性系统；当b<0时，频率-位移响应曲线向右弯曲，称为硬弹簧特性非线系统；b=0时即为线性振动系统。相对于线性系统频率-位移单值对应的特点，非线性振动系统频率-位移响应曲线的弯曲特性可使系统在较宽频带范围有大的位移输出，从而实现振动能量采集器的拓频，但这也会带来解的不稳定性，如图中虚线部分，同一频率对应位移并非单值，如何引导系统向大幅位移高能输出轨道运行是基于非线性振动的压电能量采集器需要重点研究的问题。

非线性系统包括单稳态系统、双稳态系统等，这主要与系统势函数相关。不同的势能函数可得到对应非线性系统势能函数曲线，依据式(2)，可得基于Duffing振荡器的势函数曲线，曲线如图2所示。

图2 势能函数曲线

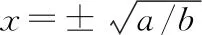
1.2 非线性压电俘能器机电耦合理论

2005年，Lefeuvre[8]等建立了线性压电俘能器的机电耦合方程；2009年，Stanton[9]等在随机激励条件下，建立了非线性压电振动能量收集器机电耦合方程，基于此，可建立压电俘能器在不同激励条件下的机电耦合方程：

(4)

式中：α为机电耦合系数；CP为等效电容；R为负载电阻；V(t)为输出电压；f(t)为外界激振力。

势函数U(x)的不同则可以得到不同类型非线性压电俘能器耦合方程。耦合方程通常具有强非线性特性，难以获取解析解，通常只能以近似解析结果或数值解分析俘能器响应性能。

2 非线性压电俘能器研究现状

依据不同分类方法，可得到不同的非线性压电俘能器，依据是否具有多方向俘能功能可分为多方向压电俘能器和单方向压电俘能器；依据势能函数特性有单稳态和多稳态压电俘能器；依据不同非线性引入方式可分为基于外力耦合、基于非线性应变、基于分段线性等的压电俘能器。文中主要从不同非线性引入方式，结合其他分类对非线性压电俘能器研究状况进行综述。

2.1 基于外力耦合的非线性压电俘能器

非线性外力耦合压电俘能器主要是通过施加外力场来改变俘能器刚度，使系统呈非线性，最常见的类型就是在悬臂梁结构中引入磁力。2009年，A.Erturk等[10]采用F.C.Moon和F.J.Holmes[11]提出的磁力双稳态模型用于压电俘能器俘能研究，结构如图3所示，其通过理论分析与实验研究证明该结构在简谐激励下具有较宽的低频俘能范围，电路断态下的输出电压比线性结构高2倍，输出功率高出8倍。

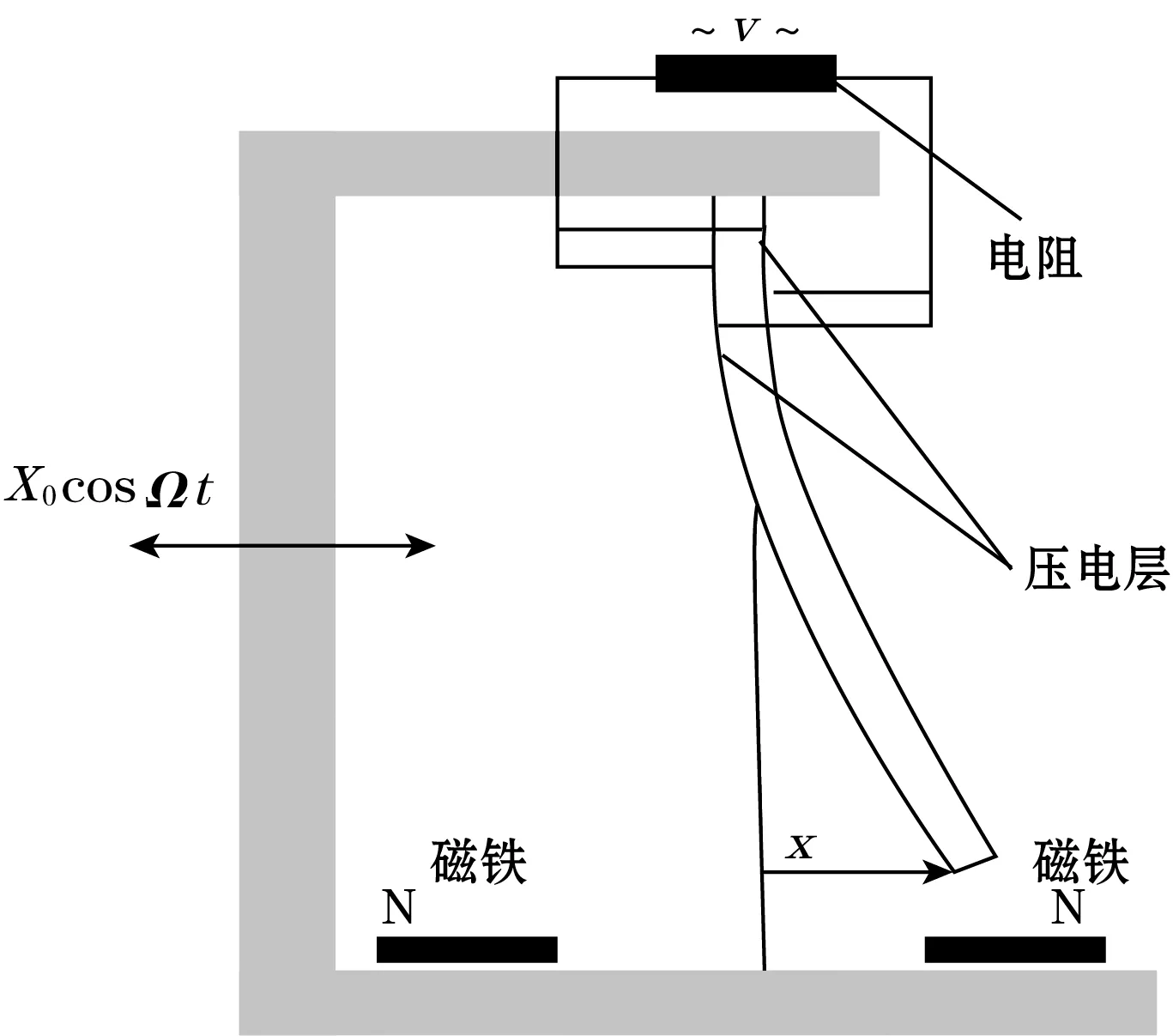
图3 磁引力作用下的双稳态俘能器

2011年，M.Ferrari 等[12]对如图4所示压电振子在随机激励下的共振位移特性进行了实验研究，理论分析了非线性对双稳态现象的影响，但没有对双稳态发电响应特性进行研究。该压电振子在悬臂梁自由端增设了一磁块，另一磁块固定布置，且与自由端磁块保持磁斥力关系，这成为双稳态压电俘能器典型结构。

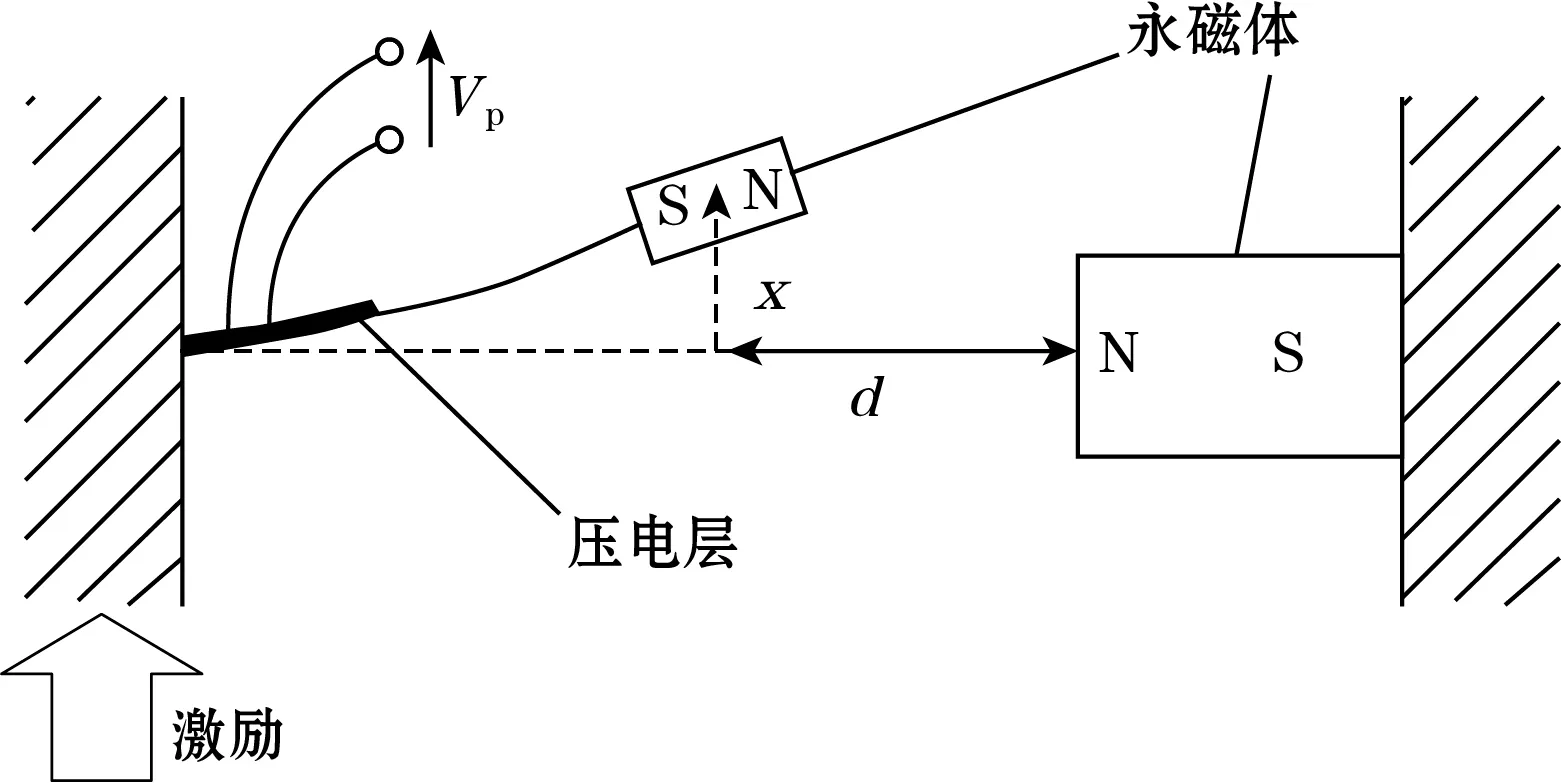
图4 磁斥力作用下的双稳态俘能器

陈仲生[13](2011年)、孙舒[14](2012年)、唐炜[15](2014年)等均对此典型结构展开了研究。

2016年，张旭辉等[16]提出基于磁力耦合的直梁加拱形梁新型组合梁结构俘能器，该结构具有结构简单、能够多方向收集能量的优点； 2018年，该团队[17]对其展开深入研究，组合梁结构如图5所示。建立了新型组合梁动力学模型，分析了阻抗、机电耦合系数、阻尼等对系统响应特性的影响，实验验证了该结构俘能器有效工作带宽是相应线性结构3.1倍。

图5 线形-拱形组合梁原理图

2017年，C. Lan[18]等其基于典型压电俘能结构，在固定磁铁上、下两端分别对称布置磁块，且与悬臂梁自由端磁块保持吸力关系，通过理论分析与实验验证了该俘能器能在弱激励下相对于典型压电振子更易实现阱间振荡，在随机激励下有更好的俘能性能。

2014年，H. Wu[19]、W. J. Su[20]、M. S. Nguyen[21]等均提出一种具有两自由度的双稳态压电俘能器，2019年，M. S. Nguyen所设计两自由度压电振子如图6所示，两自由度压电振子主要通过结构参数优化使各个自由度离散的共振频率接近，从而形成共振频率带以拓宽频率，总体来看其俘能效率优于典型单自由度压电振子。

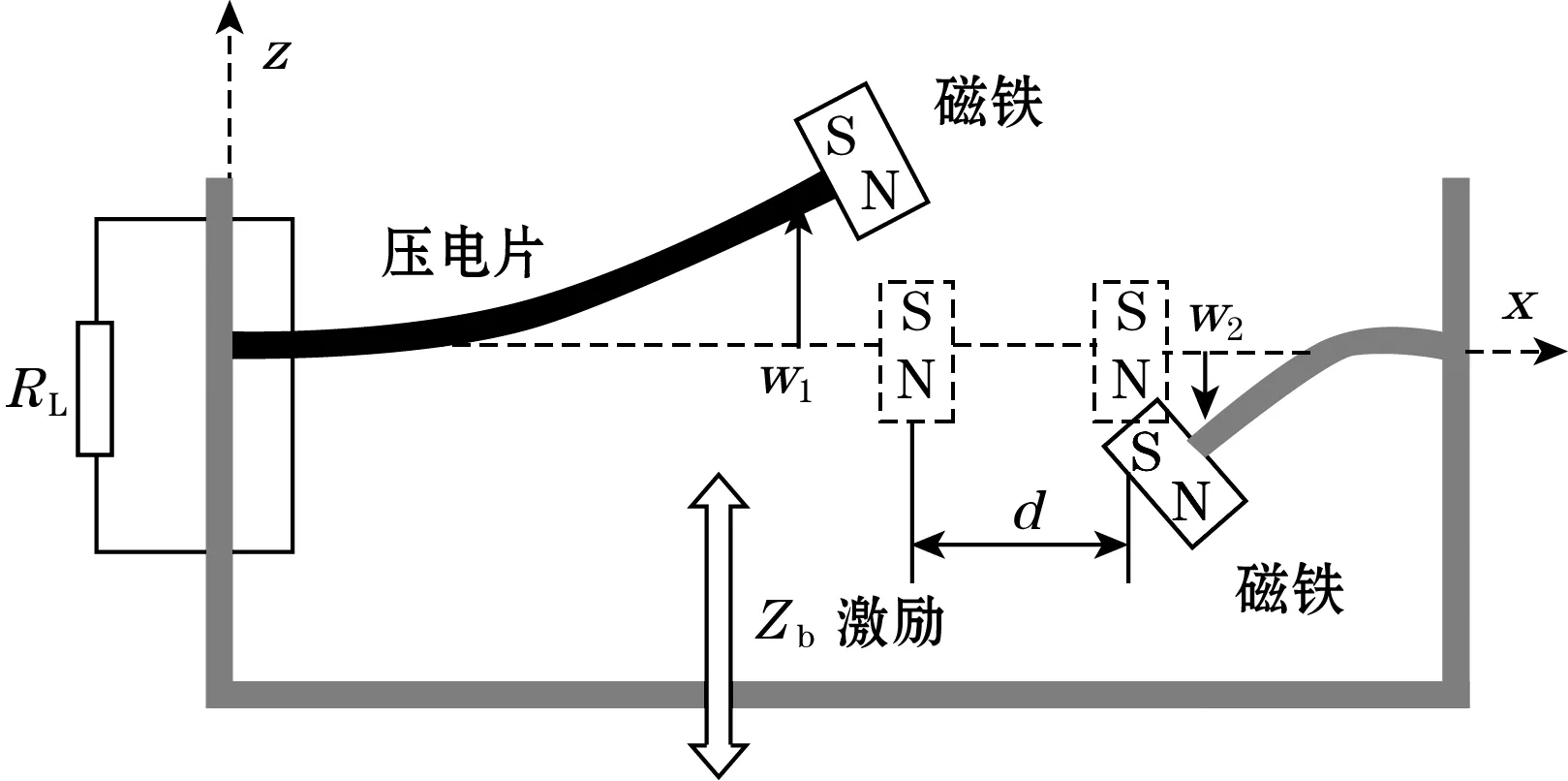
图6 两自由度非线性压电俘能器

非线性双稳态能量收集器相对于线性能量收集器具有更宽的有效工作频率范围，能产生大幅的阱间振荡而获得大的电压输出，但也存在势阱较深，需要大的激振幅值或频率才能激发阱间大幅振荡。相对于双稳态结构、三稳态或多稳态系统具有较浅的势阱，更易实现阱间振荡获得大的电压输出。

S. Zhou[22](2014年)，M. Panyam[23](2017年)，A.Kumar[24](2019年)等均对磁力引入的非线性三稳态压电俘能器展开了研究，其中S. Zhou[25-26]对三稳态压电俘能器做了系统的研究，其通过理论分析与实验验证了在简谐激励频率1～20 Hz范围内，三稳态俘能器相对于双稳态可以获得更高的能量输出。

除了将磁力引入压电俘能器外，2019年，汪灿[27]、王光庆[28]等将弹簧力引入俘能器构成非线性压电俘能器的动力学特性进行研究，仿真验证了压电振子在一定激励条件下，可以调节参数可以实现单稳态、多周期、局部双稳态、大幅值双稳态、混沌和三稳态等做多种运动，呈明显的非线性特性，俘能器结构如图7所示。该压电振子振动时，末端质量块的大位移和线性弹簧的大变形将引起能量采集器几何非线性变形，弹簧产生的恢复力与悬臂梁末端振动位移成非线性关系，导致压电能量采集器表现出非线性的复杂运动特性。

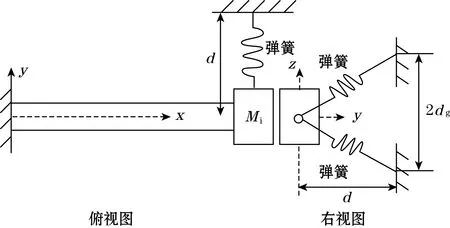
图7 弹簧力引入式压电俘能器

除此之外，还有将电磁力等引入压电俘能器构成非线性压电俘能器。

2.2 基于分段线性结构的非线性压电俘能器

分段线性压电俘能器实现非线性的原理是利用俘能器在振动过程中与限位器发生碰撞，从而改变系统等效刚度，获得分段的线性恢复力，其系统总体表现为非线性行为。2011年，K. H. Mak[29]对如图8所示具有凸起的止动器的悬臂压电俘能器进行了研究，通过数值仿真方法研究了止动器的位置、间隙距离等对系统行为及输出电压的影响。

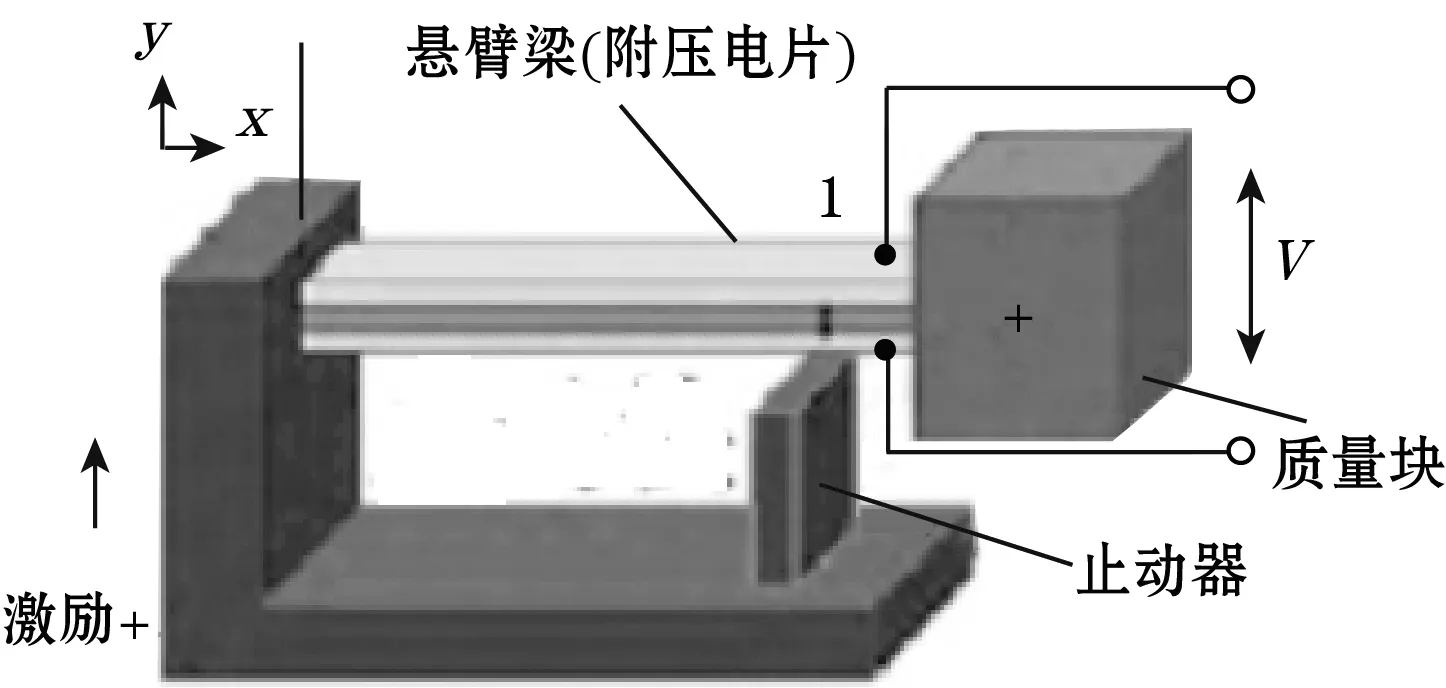
图8 分段线性压电俘能器

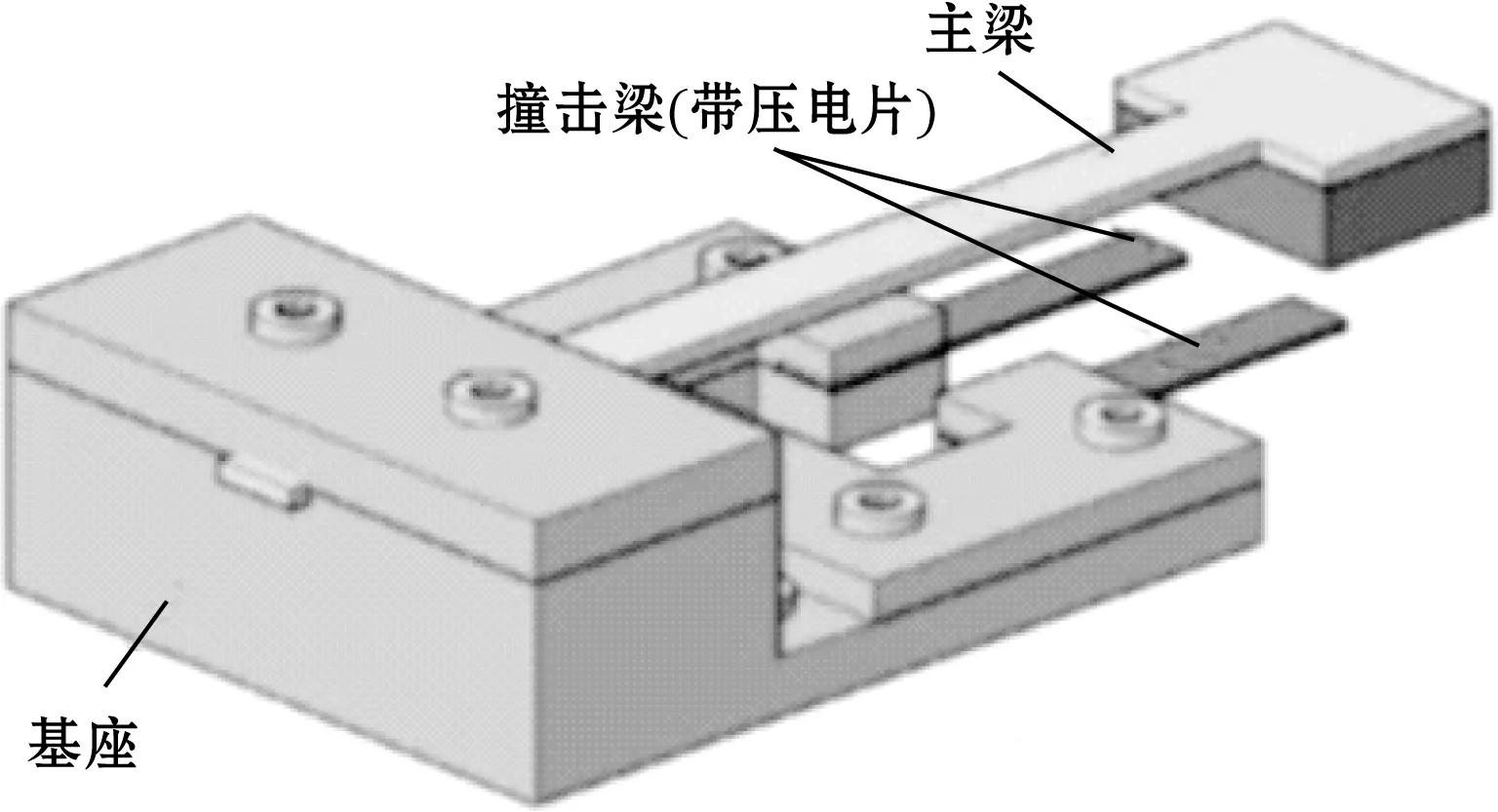
图9 分段线性结构俘能梁

2014年,M. A. Halim[30]等针对图9所示分段线性压电俘能器进行了理论分析与实验验证，其压电悬臂与普通悬臂梁相似，不同之处在与其在受到激励振动时会与主梁的质量块发生碰撞，刚度会发生分段线性变化，其研究表明该结构通过与主梁质量块发生撞击可以有效将低频振动转为悬臂梁高频振动，其综合有效工作频率范围为7～14.5 Hz，单梁压电片最小输出功率为233 μW，俘能器最大输出功率达734 μW，验证了由撞击产生的全局非线性行为能有效拓宽系统工作频率。

2016年，刘少刚[31]针对分段线性压电俘能器接入负载后，产生反馈而形成机械阻尼的实际情况进行了耦合建模分析，并验证了模型的精度。2018年，D. Zhao[32]等针对单自由度分段线性梁，采用谐波平衡法分析了其有效工作带宽、输出电压峰值等并实验验证了方法的有效性，为优化设计分段线性压电梁参数奠定了一定理论基础。

2016年，M. A. Halim[33]等针对两自由度分段线性悬臂式压电俘能器进行了研究，其结构如图10所示。俘能器主要由主梁、副梁(带压电片)以及连接主、副梁间质量块构成，这种结构有别于一般双自由度系统，当主梁与基座发生碰触后，会为副梁的振动提供动力放大，使压电梁产生大的冲击力，同时相对于直接碰撞式分段线性结构，减少了能量的损失，该结构半功率带宽与平均功率分别是普通两自由度线性梁的2.5倍和4倍。

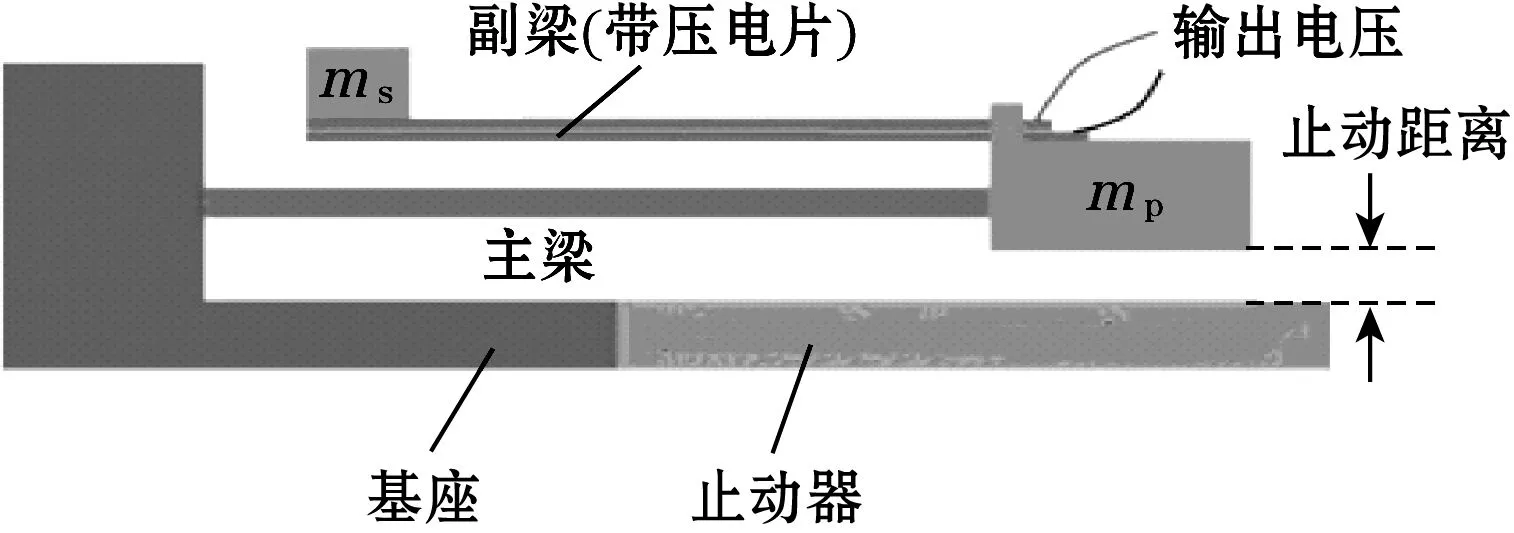
图10 两自由度分段线性压电俘能

2016年,S. Liu[34]等提出一种两自由度分段线性压电俘能器，并对结构进行了理论分析与实验研究，结果表明前两阶模态的频率带宽是相应线性压电俘能器的5.2倍，第一、二阶模态的输出功率分别达429 μW和411 μW，与单自由度分段线性压电俘能器相比，双自由度在低频时有更宽的有效响应频率，也优于双自由度线性压电悬臂梁。

2017年，G. Hu[35]等设计了图11所示具有止动器的两自由度分段线性结构。其理论分析的结果表明这种两自由度分段线性结构在加速度为2 m/s2的激振条件下，其有效工作频率是线性单自由度与两自由度压电俘能器232.1%与289.8%，最大功率输出幅值分别提高了64.4%和118.9%。

图11 具有末端止动器的压电俘能器

2019年,H. Farokhi[36]等设计基于碰撞的非线性压电俘能器，俘能器结构与普通悬臂梁结构类似，但其自由端为圆形质量块，悬臂梁振动过程中末端质量块会与基座上、下沿发生碰撞产生非线性行为，他建立了完整的非线性动力学方程对其进行了分析与验证。结果表明：该结构输出功率是无约束压电悬臂梁的263%，且增加约66.8%的共振带宽。

2.3 基于非线性大应变的压电俘能器

非线性大应变是利用机械结构产生大的形变，致使结构出现非线性应变，从而具有非线性弹簧刚度，系统响应呈非线性特性，当前主要采用预加载或摆式结构使压电梁发生屈曲变形。

2011年，R. Masan[37]提出一种两端固支的屈曲梁，当在右侧向左逐渐增大轴向载荷P后，梁将发生屈曲变形，从而在外界激励下具有宽频效应。其结构如图12所示。

图12 受轴向载荷的俘能梁

Masans针对不同载荷下的俘能器有效工作频率带宽进行了研究，且表明俘能器非线性随着轴向载荷的增加而增强，当轴向载荷减小向发生屈曲状态的临界值靠进时，俘能器非线性急剧减弱。

2012年，M. I. Friswell[38]等采用竖直放置悬臂梁结构实现压电俘能，其结构如图13所示，施加横向激励可使梁发生屈曲变形，实现双稳态俘能，随机激励的仿真结果表明该结构较线性俘能器而言，具有更好的俘能效果和有效工作带宽，但该结构不易激发阱间振荡。

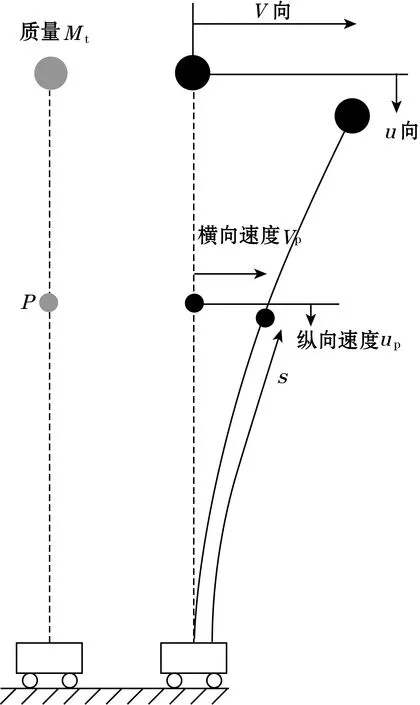
图13 纵置式悬臂梁

A. Hajati[39]等利用 MEMS提出了一种超宽频压电俘能器，其将固支梁的拉伸应变引入非线性刚度，研究表明这种俘能器频带宽度和能量密度较之前类似的俘能器高出一个数量级。A. J. Sneller[40]针对两端夹持式压电俘能器进行了研究，其结构如图14所示，梁两端用支撑夹夹持，中部施加一质量块，外部激励时，梁在质量块力轴向载荷的作用下可实现双稳状态，收集较低频率振动能量。

图14 夹持式压电俘能器

F. Cottone[41]等对屈曲梁结构压电俘能器在宽频带随机激励条件下的发电特性做了相关研究，发现屈曲状态输出功率是非屈曲状态下的 10 多倍。2017年，X. Y. Jiang[42]等设计了通过磁力诱导，使梁发生屈曲变形的非线性压电俘能器，结构如图15所示，他通过理论与实验验证了这种具有双稳态特性俘能器能在4.4 Hz以下的低频范围下产生3.6 μW的平均功率，磁极间距对于功率输出有较大影响，优化结构参数可在低频下可获得较好的俘能效果。

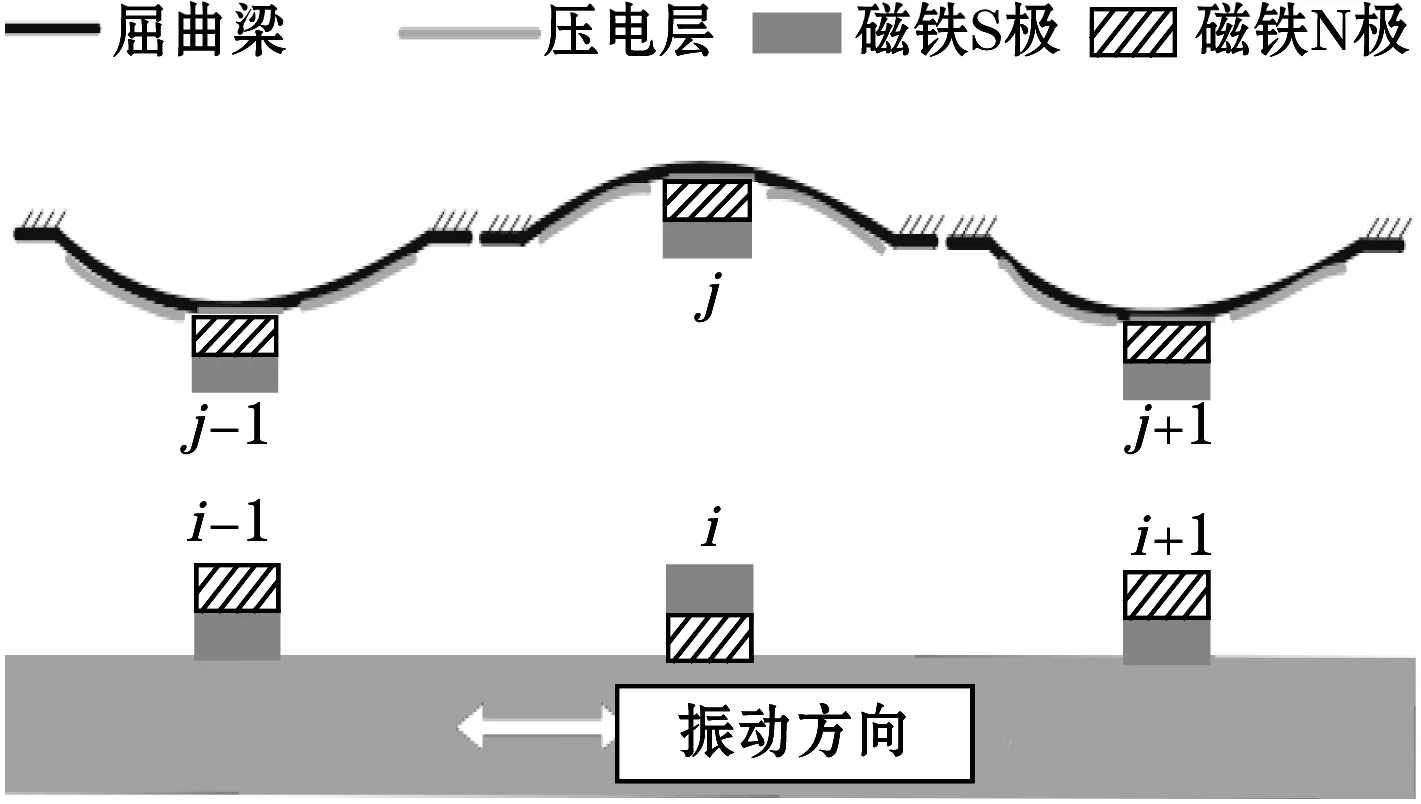
图15 磁力诱导屈曲梁

2018年，M. Darakhshani[43]等针对图16所示双稳态屈曲梁结构进行了动力学分析，该结构由扭力梁将主梁和2个带质量块的悬臂梁连接而成，扭力梁在振动时承受扭力矩，研究表明，两悬臂梁对于实现主梁的双稳态响应具有重要的作用，通过优化参数，主梁可在更宽激振力范围和更低频率下实现双稳态，有利于低频振动下的能量收集。但他没有对结构进行压电发电性能的研究。

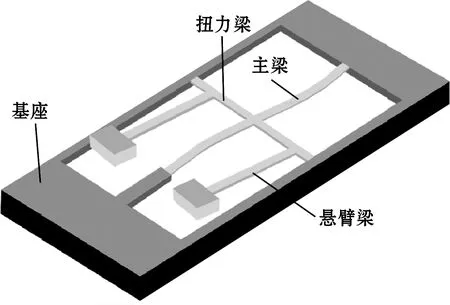
图16 双稳态屈曲梁俘能器

以上综述了最常用的非线性引入技术，除了可以独立采用外，近年来部分学者还将2种以上的非线性技术共同引入压电俘能器中实现非线性复合俘能，如X. Wang[44]、W. Yang[45]等研究均采用非线性复合俘能技术，这些技术增强了俘能器的工作效率与适应性，但同时也增加了装置的复杂性，不利于装置微型化，给系统的理论建模、分析、优化等都带来挑战。

2.4 多梁结构非线性压电俘能器

多梁结构非线性压电俘能器采用多悬臂梁排列组合而成，梁通常具有不同共振频率，形成相邻的共振频率带，以进一步拓宽压电俘能器有效工作带宽。

2009年，M. Ferrari等[46]提出采用多悬臂梁阵列式压电俘能器，俘能器结构如图17所示。装置中心布置了磁铁以引入磁力非线性，4个磁性质量块分别固定在悬架臂梁自由端，每组悬臂梁具有不同尺寸，具有不同的势能曲线以实现不同带宽的响应。他对该俘能器进行了实验研究，结果表明：施加纵向激振，加速度为1.2g时，悬臂梁在振动过程中出现大幅阱间振荡，呈非线性特性，输出功率会明显增加。

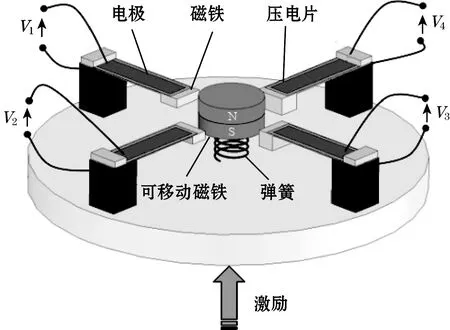
图17 圆形阵列式俘能器

2014年，W. J. Su[47]等提出基于磁耦合具有内外梁的非线性压电俘能器，结构如图18所示，该俘能器由内梁和外梁构成，内、外梁在相对布置磁铁作用下呈排斥力关系，使得梁具有两个稳态特性。他将每个梁看成一个施有磁力的单自由度系统，建立该压电俘能器理论模型。仿真和实验结果表明：该压电俘能器具有宽频响应特性，2个梁的磁铁间距d对采集器的输出功率和带宽有影响，d减小可增大谐振频率附近的输出功率，但在其他某个频段会减小输出功率，这是由于d减小磁力大，使梁无法越过2个稳态振动，产生较小的功率输出。通过外接整流电路后向一个电阻负载提供能量，结果表明在 0.3g加速度振动激励下,俘能器在整个频带内能输出0.5 mW以上的输出功率。相对于线性结构，该磁耦合双梁结构可增加主梁和副梁的带宽，主梁输出电压得以提高,但副梁输出电压略有降低。

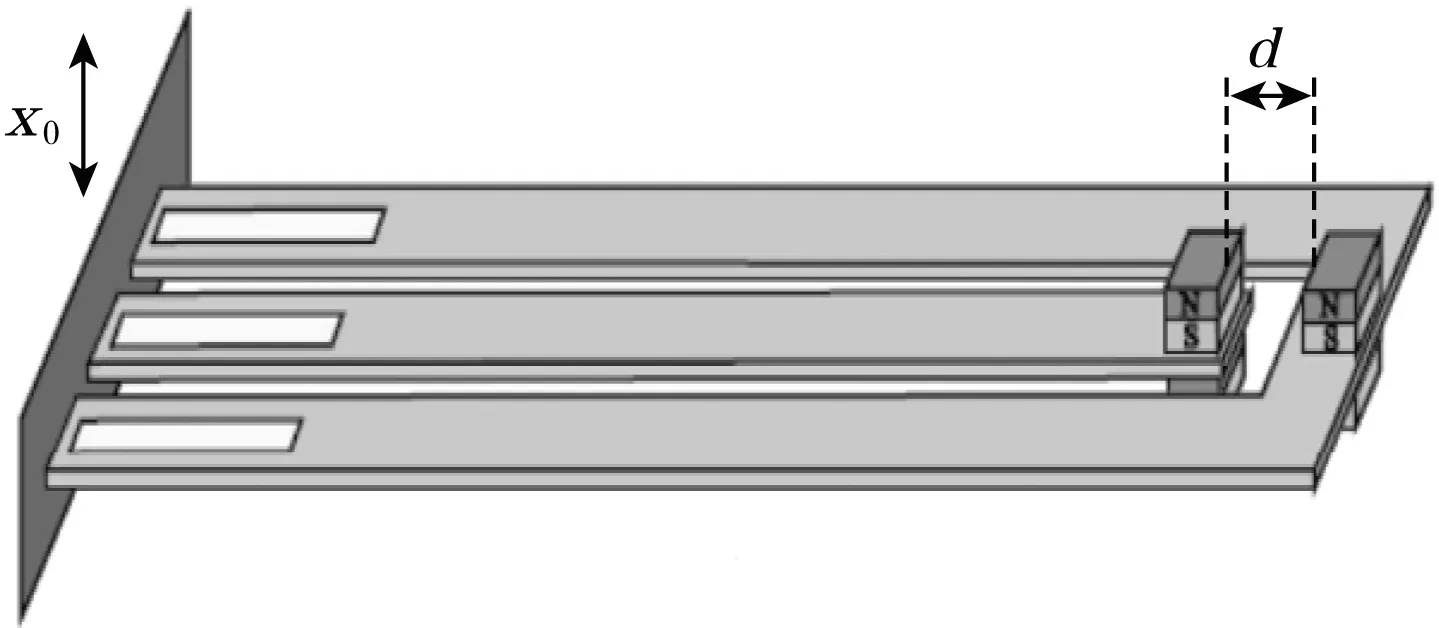
图18 双梁式压电俘能器

2015年，沈威[48]将三组悬臂梁平行布置，引入非线性磁力，设计了多梁结构的非线性压电俘能器，俘能器主要包括3组平行布置的悬臂梁，梁自由端与同一磁块相连，另一磁块固定于基座，两磁块磁力相斥。他建立系统动力学模型，研究了在简谐激励条件下，不同磁间距、不同负载与输出功率之间的关系，确定激励幅值A=0.4g，R=250 kΩ时理想磁距为d=7 mm，并在不同磁距条件下俘能器俘能性能进行了对比分析，数值仿真结果表明在激励频率低于35 Hz条件下，压电俘能器输出功率是d=30 mm时的3.3倍。

2018年，S. X. Zhou等[49]设计了一种新型非线压电悬臂梁式俘能器，其结构如图19所示，该结构中悬臂梁采用线性弹簧横向连接，通过动力学理论分析表明该结构在振动过程中出现明显的非线性特性，分别与具有2组、3组相应线性压电悬臂梁俘能特性做了对比分析，结果表明：该种具有2组和3组多梁结构俘能器的输出功率分别是相应线性结构的268.8%和339.8%,线性结构的有效工作频带分别为0.86 Hz和1.53 Hz，该结构相应有效带宽为3.30 Hz和3.51 Hz。

图19 弹性连接式多梁非线性压电俘能器

2.5 多方向非线性压电俘能器

上述均为单方向压电俘能器，其对方向的选择性很强，方向偏离后能量收集能力严重削弱，为提高收集效率，研究者积极研究多方向压电能量收集器。

陈仁文[50]等提出了一种立方体-质量块结构的全方向振动能量收集装置，结构如图20所示。该装置由1个立方体形金属框架、1个金属质量块、8个相同的Rainbow型压电换能器组成(也可以是其他换能元件)。装置受到外界环境激励时，质量块会产生受迫振动，Rainbow型压电换能器因而产生弯曲变形，使得粘贴在换能器上的压电材料随之产生变形，从而输出电荷，实现对不同方向振动能量的收集。Rainbow型压电换能器具有受环境振动方向影响小、便于安装、适应性强等优点。但该结构仍存在制作复杂、当振动方向处于装置对角线方向时能量收集效率低等缺点。

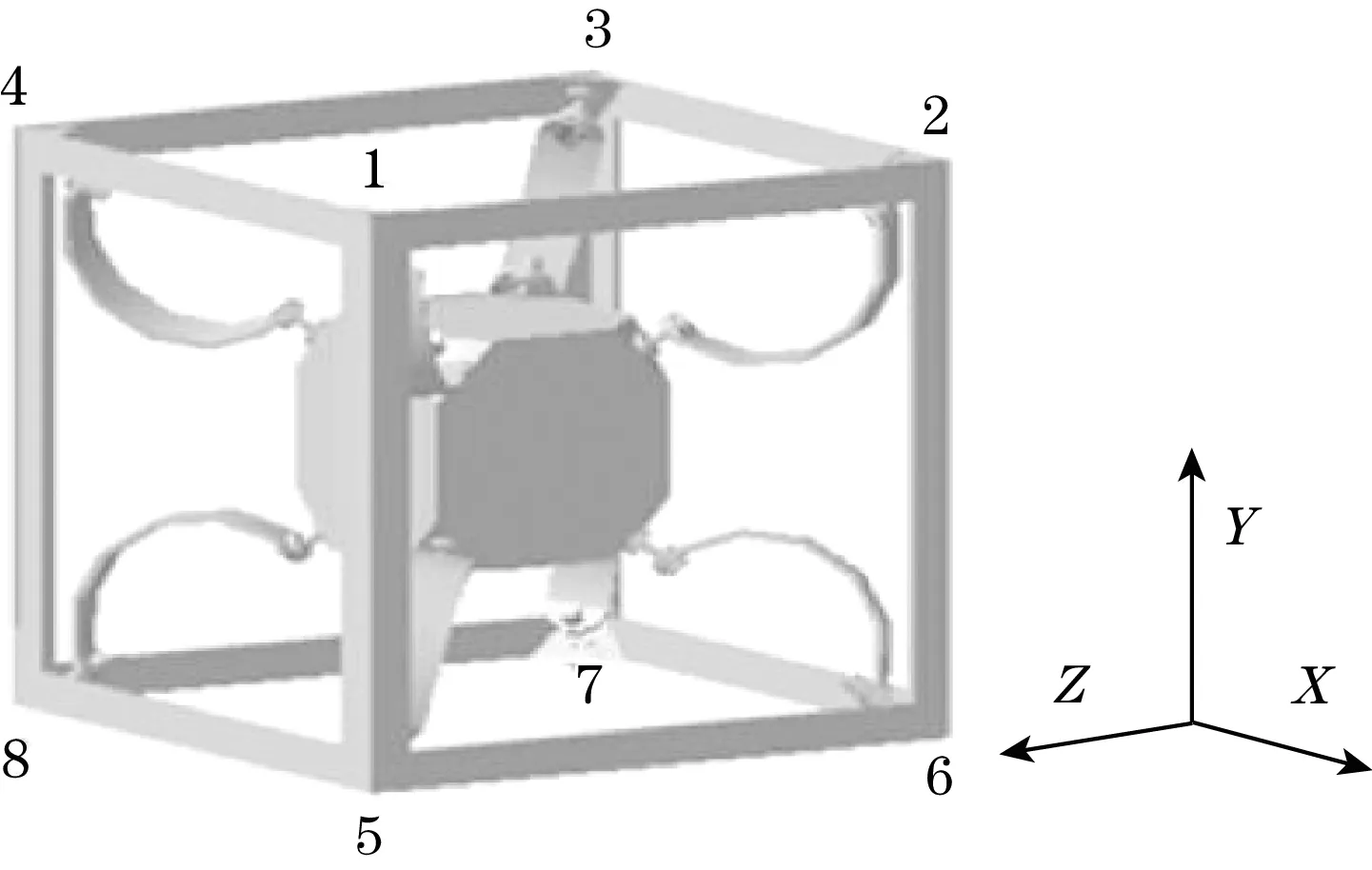
图20 立方体压电俘能器

2013年，W. J. Su等[51]设计了由1个弹簧-质量块系统、1个主悬臂梁和1个副悬臂梁组成的多方向压电器，其结构如图21所示，主梁用来感应u方向振动,副梁用来感应y方向振动，弹簧-质量块系统用来感应z方向振动，3个组成部分之间通过磁力耦合作用构成非线性系统，以实现对3个方向振动能量收集。理论和实验研究表明：在 0.3g振动加速度下，采集器3个方向的频率电压响应都呈现硬弹簧非线性特性，带宽均超过5 Hz；采集器在u和z方向振动作用下，输出的电压最高，最大幅值达到10.2 V，y方向输出电压最低，最大幅值只有2 V。

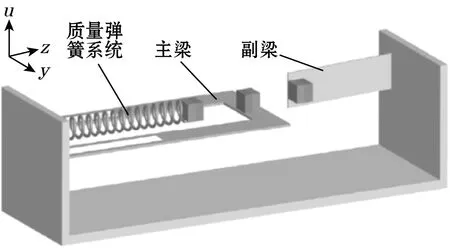
图21 三方向压电俘能器

B. Andò等[52]提出了一种两维的双稳态宽频压电俘能器.其结构如图22所示，它由2个相互垂直的压电悬臂梁组成，2个压电悬臂梁自由端均布置一磁铁，磁铁间相互排斥，排斥力使梁之间具有2个稳定状态，由于悬臂梁间存在磁力的耦合作用，任一悬臂梁发生振动都会带动另一梁振动，因此采集器可实现二维振动能量收集。他建立了俘能器机电耦合动力学模型，并根据不同振动方向对俘能器俘能性能进行了仿真和实验研究。研究结果表明：当ψ=0°时(ψ为振动方向与z轴的角度)，激励加速度必须大于60 m/s2,才能使压电梁产生振动,该值与悬臂梁结构参数密切相关，可通过优化结构调整最小加速度激励值；当加速度为 95 m/s2时，330 kΩ为压电俘能器最佳负载值,可获得5.6 μW的最大功率。

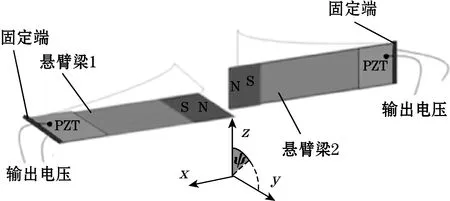
图22 双向压电俘能器

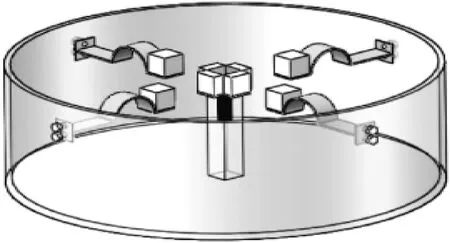
图23 组合梁结构压顶俘能器

张旭辉[53]等设计了一种磁力耦合多方向组合梁结构压电俘能器，其结构如图23所示。该组合梁结构压电俘能器具有结构简单，能够响应纵向、横向多方向激励的优点，他利用广义Hamilton变分原理建立了系统分布式力-电-磁耦合模型，结合数值计算和实验验证方法体现了磁铁间距、外界激励条件对压电俘能系统响应特性的影响规律。

张旭辉等[54]团队设计了另一种多场耦合多方向压电俘能器，该结构较前一种俘能器结构更加紧凑，其结构如图24所示。该俘能器由4个线形-拱形组合梁、永磁铁质量块和可调磁铁组成，线形-拱形组合梁以金属梁为基层，其表面贴有压电换能元件，4个组合梁拱形端分别连接永磁铁质量块4个面，线形端固定在外壳上。外壳上下表面通过调节螺纹可调整磁铁间距。他建立了俘能器力、电、磁耦合非线性动力学模型，并进行横向激励、纵向激励下俘能特性进行分析，结果表明：当施加纵向激励，磁铁间距为15 mm、激励幅值0.5 m/s2时，相比无磁力输入的情况，系统响应电压提高了6倍左右，谐振频率从18 Hz降至9.5 Hz左右，有效改善了压电俘能器俘能性能；施加横向激励时，由于系统横向刚度大于纵向刚度，系统横向振动响应会受到磁吸力的作用减小，输出量远小于纵向振动的输出电压。

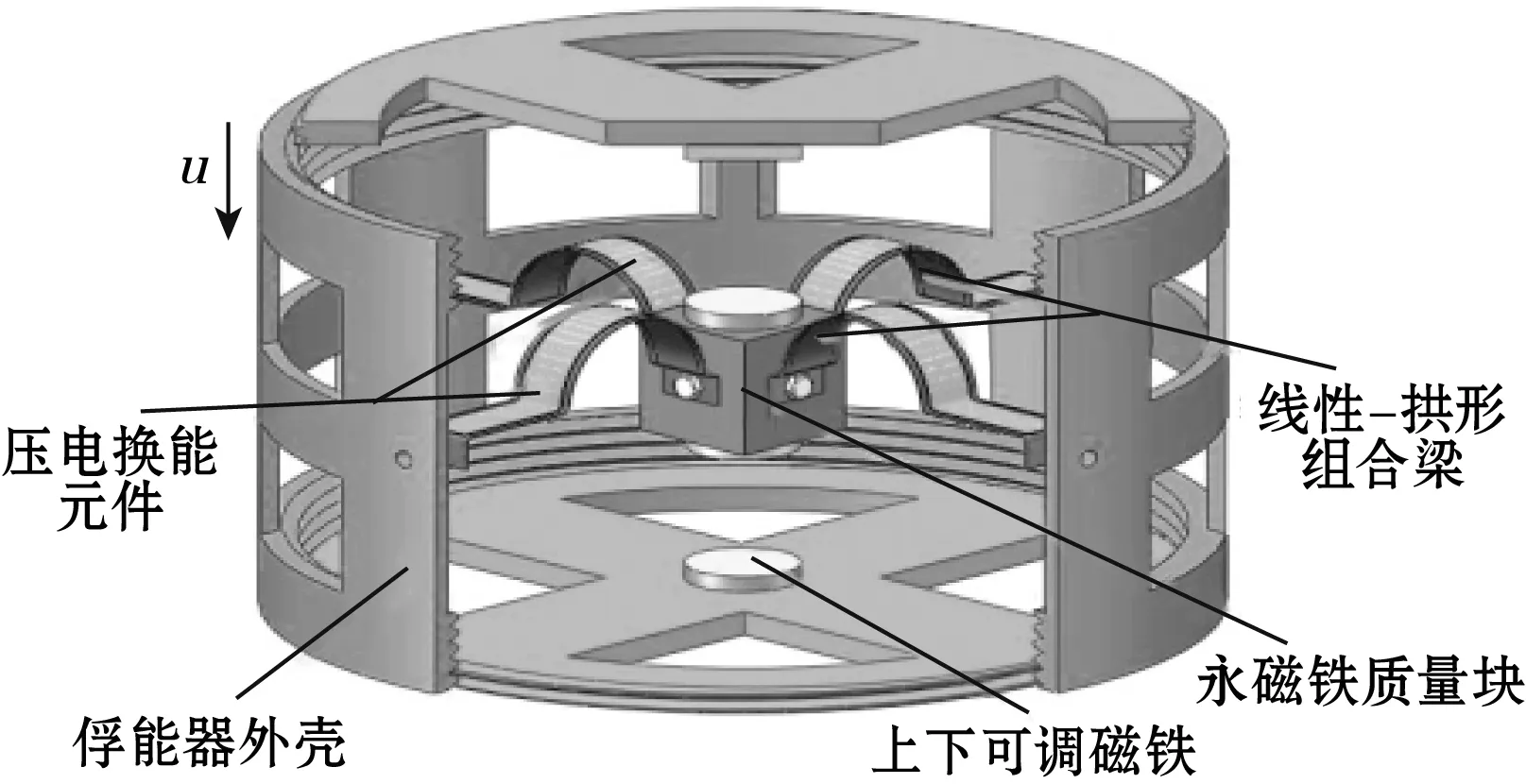
图24 多场耦合多方向压电俘能器模型图

3 各类非线性压电俘能器性能比较分析

非线性双稳态俘能器是当前研究常采用的结构形式，双稳态阱间振荡能有效提升俘能效率。但双稳态有较深的势阱深度，弱激振难以激起双稳态响应，得到有效的输出，低水平激励使得其相对于线性俘能器并无优势；总体来说，相对于线性压电俘能器，非线性压电俘能器能拓宽有效工作频率，提高俘能效率。各类非线性压电俘能器存在不同特点，针对各类俘能器特性进行分析如下：

(1)基于磁力引入的非线性多稳态压电俘能器容易调节磁距改变非线性特性，使得其有较强的适应性，但适宜激励条件的势阱深度不易获取，过低的势阱深度将会使装置接近于单稳态系统而难以拓宽有效工作频带。

(2)分段线性压电俘能器不需引入其他力场即可实现，其局限在于俘能器在撞击过程有能量损失，会限制俘能器最大响应幅值，而得到有限功率输出。同时，长期的撞击对于悬臂梁刚度、系统稳定性的影响也值得考虑。

(3)基于非线性大应变的压电俘能器常通过预加载方式实现，这可以放大外部激励对装置的影响作用，降低共振频率，拓宽俘能器有效工作频带。但也存在前述双稳态压电俘能器存在的特点，且长期预加载力导致的机械结构形变易影响系统性能。

(4)基于多梁结构的非线性压电俘能器是非线性与多模态拓频技术的综合，采用不同的结构参数形成相邻的工作频带以拓宽整体有效频带，但多梁结构必然带来装置的复杂性，体积较大不利于微型化。

(5)基于多方向的非线性压电俘能器通常采用多个振荡器来拾取相应方向的振动，减弱了压电俘能器对方向的依赖性，但是目前多方向压电俘能器各方向间收集效率不一，相差较大；总体收集效率依然较低，且装置体积较大，制作、装配复杂。

4 非线性压电俘能技术发展趋势

压电俘能技术是一种绿色、可持续发展技术。工作带宽窄、俘能效率低是制约其应用的关键因素。非线性技术的应用对压电俘能技术的发展起到促进作用，综合前文所述，本文认为针对非线性压电俘能技术发展，可在以下方面深入展开：

4.1 理论模型的完善

非线性压电俘能技术理论模型构建是建立在一系列假设与简化基础上，使得理论模型还不能精确反映压电转换过程，下一步可从压电转换本质规律。

4.2 高效求解算法研究

非线性压电俘能器理论模型复杂，涉及参数较多，多为强非线性微分方程，由于相应求解工具尚不完备，故求解结果多为近似结果，尤其对于随机激励条件下的响应性能的分析、获得准确结果更困难。探索高效、先进求解算法，通过理论模型和求解方法的结合，以获得准确定量分析结果，揭示非线性参数与系统能量转换的本质规律。

4.3 双稳态系统俘能性能研究与改善

非线性双稳态系统是当前研究热点，其具有易实现、结构简单等特点，是未来研究的重点方向，但其仍有以下问题亟待解决：如何降低势垒阈值，低水平激励下实现阱间振荡以充分发挥俘能效率；由于多解的存在，如何确保双稳态系统处于俘能高能轨道上运行值得深入研究。

4.4 基于非线性技术与振源特性的俘能器一体化设计研究

特定应用背景的振源有其相应特性，而不同非线性技术有相应的性质，基于振源特性分析，结合非线性技术性质，展开压电俘能器一体化设计、优化，使非线性技术的研究更具针对性。

4.5 与其他技术的结合研究

当前压电俘能器转换效率仍然较低，可结合新型压电复合材料、能量收集电路等技术的研究综合提高能量转化效率，以期压电俘能器早日投入工程化应用。

5 结论

本文对非线性压电俘能器的研究现状进行了综述，对当前不同非线性压电俘能器进行了总结，分析了其相应的特点，并基于研究现状对未来的发展趋势进行了简要概述。目前非线性压电俘能器的研究已取得了较大进展，但当前研究主要集中于结构的设计、特定类型激励或条件下俘能性能的研究。在这些条件下，即使非线性压电俘能器展现了较好的拓频性质，但与俘能器实际工作环境仍存在较大的差距。今后研究应充分结合振源性质、能量收集电路、转换电路等进行综合、系统的研究，使理论研究尽可能与实际的情况吻合。