自适应多启发蚁群算法的无人机路径规划

尹雅楠 甄然 武晓晶 张春悦 吴学礼

摘 要：为了解决蚁群算法在无人机实现路径规划中容易陷入局部最优的问题，提出改进的蚁群算法。对信息素的挥发因子以及信息素进行上、下限设置，防止由于较短路径上的信息素过高以及较长路径上的信息素过低，使蚂蚁陷入局部最优，同时在多启发因素的影响下，将路径的整体长度作为决定状态转移概率的一个自适应启发函数因子，当路径长度很大时，自适应启发函数因子较小，使得蚁群选择该路径的概率减小。实验结果表明，改进的算法在路径长度上减少了6.4%，最优路径长度方差降低了85.78%，增加了对环境整体性的考虑，缩短了路径长度，降低了迭代次数，跳出局部最优。在环境复杂度加大的情况下，引入自适应启发函数因子之后的算法可以有效地选择较好的路径，为无人机路径规划提供了理论依据。

关键词：航空、航天科学技术基础学科其他學科;无人机;蚁群算法;路径规划;启发因素

中图分类号：TP301.6;V279 文献标识码：A

文章编号：1008-1542（2021）01-0038-10

随着现代科技的发展，无人机可执行的任务逐渐增多，例如无人机可以承担起运输医疗救援包等应急物资的任务[1]。为了使无人机能够更好地在实际中应用，学者对无人机的路径规划进行了大量的研究，提出了很多算法来提高路径规划的效率，目前有人工势场法[2]、A*算法[3]、蚁群算法[4]、遗传算法[5]、粒子群算法[6]、蝙蝠算法[7]、模拟退火法[8]、快速扩展随机树算法[9]、D*算法[10]、人工鱼群算法[11]、蝗虫算法[12]以及萤火虫算法[13]等。遗传算法是用编码来表示问题的解，在编码进行选择、交叉、变异等操作之后，将适应度函数的值作为进化的评价依据，最后得到最优的种群，也就是问题的解[14]。蚁群算法与遗传算法在选择最优解时，操作相似。蚁群算法也是通过迭代寻找最优解，但是蚁群算法在选择最优解时没有交叉和变异这2个操作，所以求解更简单。

蚁群算法是一种基于启发的搜索算法，是由DORIGO等于20世纪90年代初通过模拟蚂蚁群在环境中的觅食行为而提出的算法[15]。蚁群算法具有正反馈、并行计算、鲁棒性好等特点[16]，许多学者在研究路径规划方面的问题时，将蚁群算法应用其中，并且得到了较好的结果。蚁群算法搜索范围广，有较快的收敛速度，可以应用在离散优化的问题上[17]，但是由于该算法具有正反馈特性，可能会造成局部路径上的信息素堆积，从而存在陷入局部最优等问题[18-19]。蚁群算法通过将当前位置与下一位置之间的距离作为启发信息，当遇到障碍物时，在提前躲避障碍物方面还存在一些问题[16]。对于蚁群算法的不足，许多学者对算法本身的不足进行改进。随着研究的不断深入，结合路径规划的特性，学者将如何提高算法的搜索效率作为研究的重点[20]。

路径平滑能够降低无人机的飞行风险，HUANG等[21]引入K度平滑方法，生成光滑的路径。TAO等[22]因当前节点与多个相邻节点的距离完全相等，导致在选择下一个节点时启发不能发挥重要作用，于是提出将起始点与目标点之间的最短距离作为路径搜索的引导，通过计算当前节点和下一个待走节点的距离和下一个待走节点到最短路径的垂直距离的加权和的倒数，加快了算法的搜索。孙功武等[23]设计了一种自适应启发函数，该启发函数引入了当前栅格与待走栅格的距离以及待走栅格到目标栅格的距离选择较好的节点，但是该自适应启发函数只考虑当前栅格以及待走栅格到目标栅格的距离。黄心等[24]根据多尺度路径搜索的思路，提出了改进后的引导因子，该引导因子考虑了节点到目标点的距离以及节点到起始点的距离，同时通过地形的高度决定无人机的飞行，但只局部考虑了启发函数的引导作用。李理等[25]在路径平滑问题上，将转弯次数引入启发函数中，对改进的启发函数进行影响，同时对信息素的更新方式也进行了改进，路径平滑性得到较大提高，收敛性和全局搜索能力都较好，但是转移概率只受信息素和启发函数的影响，迭代次数较大，容易陷入局部最优。

文献[21]在对路径平滑问题上引入K度平滑方法，而文献[25]不仅将平滑问题考虑到启发函数中，还将路径的转弯次数考虑到启发函数中;文献[22]对转移概率进行了改进，保证了算法的收敛速度，以提高算法的性能，但是所得到的路径长度不是最短的;文献[23]根据当前栅格与目标栅格的距离设计了自适应启发函数，但是只考虑了路径长度这一因素，文献[25]的启发函数考虑了多个启发因素;文献[24]将节点的引导因子引入到转移概率中进行改进，但是没有对启发因素进行改进。文献[25]在使路径尽可能短的同时，对路径的转弯次数以及路径平缓性进行考虑，进而提出了将距离修正函数、安全性函数以及平滑性函数这3种因素考虑到启发函数中的多启发因素蚁群算法。在蚂蚁寻找最优路径时，以多启发因素为基础选择路径。

但是文献[25]中的路径因素只考虑了当前栅格的各个邻接栅格到目标栅格的距离，没有从路径的整体性考虑。本文在多启发因素的作用下，从路径的整体性考虑，将文献[24]的引导因子引入转移概率中，并对启发函数、信息素和信息素挥发因子进行处理，增加算法的准确性。仿真结果表明，该方法提高了路径搜索效率，降低了迭代次数，路径长度得到改善。

1 环境建模

本文采用二维栅格法[26]对路径环境建模。考虑到无人机的安全问题，将无人机路径与栅格障碍物之间的距离定为栅格长度的一半。每个栅格有8个邻接栅格[27]可以走，如图1所示。dis（i，j）表示当前栅格i到其第j个邻接栅格的距离。

蚂蚁选择下一栅格的流程如下。

2 多启发因素

文献[25]基于路径规划需要路径长度短、转弯的次数不宜过多、路径尽量平缓以及适应环境性等问题，提出将距离修正函数、安全性函数以及平滑性函数这3种因素考虑到启发函数中。距离修正函数使当前栅格的各个邻接栅格到目标栅格的距离差值增大，在选择下一个待走栅格时，增加路径长度对蚂蚁的启发。安全性函数对无人机飞行中的转弯有一定的引导作用，当无人机当前的方向与上一时刻的方向相同时，该方向的安全性函数值就较大。平滑性函数会给无人机选择平缓路径的启发。

2.1 距离修正函数

2.2 安全性函数

在无人机飞行过程中，如果规划的路径转弯次数较多，不仅使无人机飞行的路径距离增加，还会增加无人机飞行的危险程度。尽可能地减少无人机的转弯次数，对路径规划来说是有必要的。

式中：j∈allowedi;rij（t）为安全性函数;u为启发常数;θ表示安全性的重要程度;visitedi为第t次迭代过程中，第k只蚂蚁走到当前第i号栅格时所走过的栅格号的集合;v为当前第i号栅格的上一个栅格的标号，v=visitedi（end-1）;J（allowedi）表示当前栅格的可行邻接栅格的数量;drvi（t）表示在第t次迭代时，从第v号到第i号栅格的方向转向;drij（t）表示在第t次迭代时，从第i号到第j号栅格的方向转向。通过drvi（t）和drij（t）的比较，如果两者相同，则会增大下一步沿同一个方向走的可能性，从而使路线能够较好地保持直线。

2.3 平滑性函数

式中：hmax为当前第i个栅格的高度与其邻接栅格的高度之差的最大值;hmin为当前第i个栅格的高度与其邻接栅格的高度之差的最小值;h（i）为栅格高度。

3 改进的蚁群算法

本文让蚁群在构建的栅格图中根据信息素、启发函数以及转移概率，从当前栅格的8个相邻栅格中选择下一个要走的栅格，寻找一条从起始点到目的点最近的路径。在蚁群开始寻找路径之前每栅格的信息素是相同的，蚂蚁通过转移概率选择下一个待走栅格行走，走过的路径会留下信息素，没有走过的路径的信息素会在迭代中不断减少。同时间内，较短路径上的蚂蚁很快就找到食物，而较长路径上的蚂蚁找到食物较慢。因此，較短路径上蚂蚁留下的信息素总和较多，从而吸引更多的蚂蚁来走这条路径，也就找到了最短路径。

3.1 转移概率

蚁群算法的转移概率受启发函数和蚂蚁留下的信息素这2个因素影响。在实际环境中有障碍物存在，多启发函数可以使蚂蚁对障碍物进行躲避、选择较短的路径以及减少转弯次数等。存在较多信息素的路径会引导许多蚂蚁选择该路径，当过多的蚂蚁从同一条路径行走时，在蚂蚁没有找到最优路径的情况下，认为当前路径为全局最优，从而使蚂蚁陷入局部最优。

3.1.1 自适应启发函数因子

为了能够提高蚂蚁搜索路径的效率，跳出局部最优，本文在转移概率中引入了自适应启发函数因子，见式（5）。自适应启发函数因子是待走栅格到起始栅格的距离与待走栅格到目的栅格的距离和的加权倒数。在待走栅格与目标栅格距离的基础上，再加上待走栅格到起始栅格的距离，即在考虑该待走栅格是否为最佳待走栅格时，将自适应启发函数因子作为转移概率的影响因素之一，增加对环境的整体性考虑。

式中：μij为自适应启发函数因子;dAj为起始点与待走栅格的距离;A为起始点;j为待走栅格标号;djE为待走栅格与目的点的距离;E为目的点;a，b为权重系数。待走栅格与起始点以及待走栅格与目的点的距离越小，自适应启发函数因子越大，转移概率相应地越大，从而能较好地选择较短的路径。

通过对转移概率引入自适应启发函数因子，使得蚂蚁尽可能地选择最短路径，加快搜索路径的效率。

3.1.2 改进的转移概率

改进后的转移概率：

式中：k为蚂蚁的标号;i为当前栅格号;j为将要走的下一个栅格号;t为当前的迭代次数;τ为信息素强度;η为启发函数;α为信息素重要程度因子;β为启发因子;allowedk为蚂蚁k下一步可以选择的栅格。后面的蚂蚁会根据前面蚂蚁留下的信息素来其行走进行引导，路径越短，蚂蚁留下的信息素越多，信息素同时也会蒸发，信息素的更新方式如下：

3.2 启发函数

在启发函数中加入当前栅格到其邻接栅格的欧式距离，作为影响启发函数因素之一。通过距离修正函数，在当前栅格的邻接栅格中选一个距离目标栅格最近的邻接栅格。当前栅格到其邻接栅格的距离不完全相同，为了能够更加准确地考虑路径长度对蚁群选择下一栅格的影响，在启发函数中加入当前栅格到其邻接栅格的欧式距离d（i，j）。当d（i，j）距离较大时，[SX（]1d（i，j）[SX）]的值则会减小，使得多启发函数值ηij（t）减小，进而影响转移概率的值，构成了一个闭环反馈。启发函数见式（12）。

4 算法仿真

4.1 算法流程

步骤1：对栅格地图进行构建，设置起始点A和目的点E的坐标。

步骤2：初始化参数，将所有蚂蚁放在起始点上，构建禁忌表。

步骤3：根据式（12）计算启发函数以及根据式（6）计算转移概率来确定蚂蚁下一个要走的栅格，将走过的栅格号放禁忌表中。当蚂蚁到达目的点时，即完成一次搜索，记录本次迭代的最优路径。

步骤4：根据式（9）对信息素进行更新。

步骤5：对各次迭代的最优路径进行比较，确定目前最优路径。

步骤6：判断迭代次数是否达到最大，若达到最大，则输出结果，否则继续进行迭代。

根据以上步骤的描述，给出部分改进蚁群算法的伪代码如下：

算法流程图见图4。

4.2 参数设定

为了能够更好地进行数据对比，本文参数的选取是在对比算法所采用参数的基础上进行的更改，并根据经验不断地运行调试，找到合适的数值。初始化参数见表1。

4.3 仿真比较

为了提高转移概率的可靠性，本文对转移概率进行了改善，引入了自适应启发函数因子，并将当前栅格到其邻接栅格的欧式距离作为启发函数的影响因素之一。

由于本文采用的算法是一种启发式随机优化方法，为了验证

算法改进之后的有效性，本文用MATLAB7将改进的算法与文献[25]进行了30次的仿真比较，研究的地形环境分别在10×10以及30×30的栅格障碍物地图上。

4.3.1 10×10栅格环境下的仿真

如图5所示，虚线为文献[25]的最优路径，实线为本文改进蚁群算法的最优路径，从图中可看出路径大部分是重叠的。但是从路径整体效果来看，实线的转弯次数为4次，虚线转弯次数为6次。在虚线第4次转弯时，实线保持原路径方向继续前进，路径的平滑性较好。

图6为不同迭代次数時最优路径长度的比较。在开始时，实线的路径长度比虚线的路径长度长，但是在进行迭代之后，实线较快地找到了较短路径，而虚线在相同迭代次数下，找到的路径长度并不是最佳的。

图7为不同迭代次数时最优路径的高度均方差的比较。开始时，实线与虚线的初始值相同，随着迭代次数的增加，可以看出实线的高度均方差在迭代5次以内达到稳定值，而虚线在迭代5次以外达到稳定值。

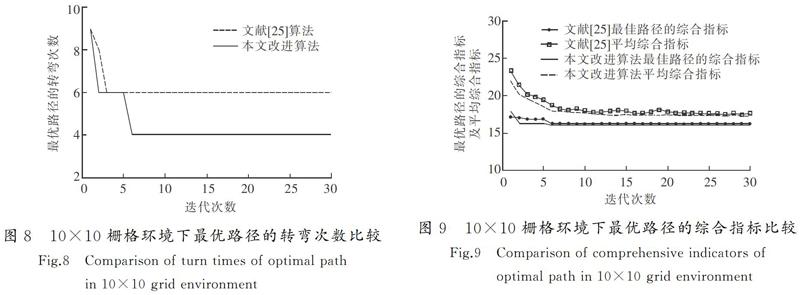
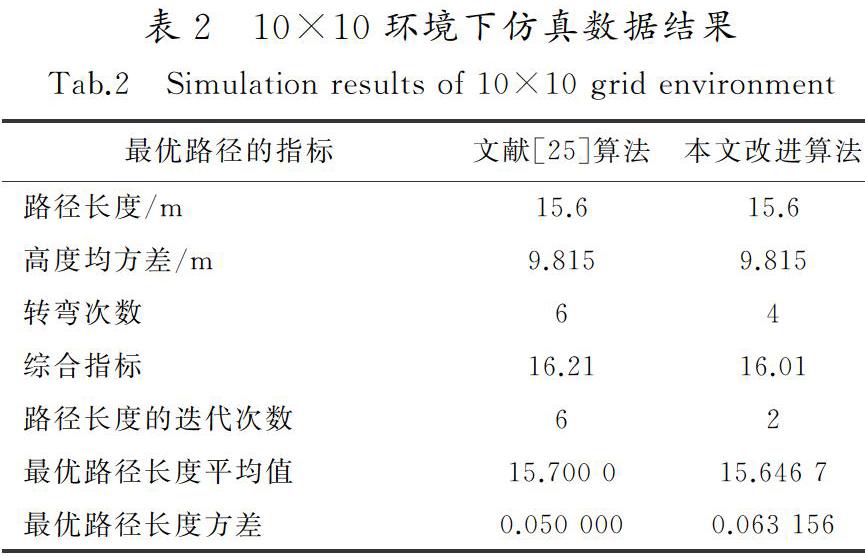
图8为不同迭代次数时最优路径的转弯次数的比较。从图8中可以看出，实线和虚线初始在同一迭代次数下，转弯次数是相同的，当迭代次数大于5时，随着迭代次数的增加，引入自适应启发函数因子的实线得到一个新的较少的转弯次数，而虚线保持原来的转弯次数，表明改进的蚁群算法增加了蚁群对路径环境的整体性考虑，跳出了局部最优。

图9为不同迭代次数时最优路径的综合指标以及平均综合指标的比较，综合指标即为距离修正函数、安全性函数以及平滑性函数的综合评价，指标越低则算法越优。从图9可以看出，本文改进算法最优路径的综合指标在初始时的值较大，随着迭代次数的增加，较快地收敛到稳定值。

通过表2可以看出，本文的改进算法降低了迭代次数，综合指标相对较小。为了减少算法随机性对实验结果带来的影响，本文在运行30次的情况下，对最优解的平均值以及方差进行了计算，如表2中的最优路径长度平均值以及最优路径长度方差所示。对于最优路径长度平均值之间的比较，从数据上看，差别不太大，为了更充分地体现差别，同时考虑到实际无人机飞行环境是复杂的，所以继续加大复杂程度，将环境建立在30×30的栅格环境中。

4.3.2 30×30栅格环境下的仿真

如图10所示，虚线为文献[25]的最优路径，实线为本文改进算法的最优路径。从图10可看出，在第二次转弯的地方，虚线的路径为直线，而实线的路径为斜线，实线的路径长度较短。从路径整体效果来看，实线的转弯次数为19次，虚线转弯次数为16次。从路径的整体性考虑，虽然转弯次数增加了，但是路径的长度减少了。

图11为不同迭代次数时最优路径的长度比较。从图11中可以看出，在引入自适应启发函数因子的情况下，开始迭代时，本文改进算法的路径长度较短，经过迭代后，很快找到较短路径并且达到稳定值。从结果可以得出，本文算法增加了蚂蚁考虑路径整体性的能力，并且提高了蚂蚁搜索路径的效率。

图12为不同迭代次数时最优路径的高度均方差的比较。开始时刻，实线与虚线的初始值相同，随着迭代次数的增加，可以看出实线的高度均方差在迭代次数10以内达到稳定值，而虚线在迭代次数10以外达到稳定值，而且实线达到稳定值的速度较快。

图13为不同迭代次数时最优路径的转弯次数的比较。从图13可以看出，由于引入自适应启发函数因子，蚂蚁选择路径时考虑路径整体性，所以实线较为平缓，波动不太大。

图14为不同迭代次数时最优路径的综合指标以及平均综合指标的比较，指标越低则算法越优。从图14可以看出，本文改进算法最优路径的综合指标曲线整体较为平缓，并且随着迭代次数的增加，较早地趋于稳定值。

通过表3中路径长度、高度均方差、转弯次数、综合指标以及路径长度的迭代次数等数据结果可以看出，改进的蚁群算法找到的路径长度相对较短，并且在路径长度的迭代次数上，改进的蚁群算法的迭代次数相对较少。

5 结 语

蚂蚁在栅格环境中寻找路径时，当前栅格到其邻接栅格的距离不完全相同。

为了能够更加准确地考虑路径长度对蚁群选择下一栅格的影响，本文在启发函数中加入当前栅格到其邻接栅格的欧式距离，增加了启发函数的影响因素，构成了一个闭环反馈，同时在转移概率中引入自适应启发函数因子，即将起始点到待走栅格再到目的点的距离作为蚂蚁选择下一个栅格的转移概率影响因素之一，增加了对环境整体的考虑，并对信息素以及信息素挥发因子进行改善，减小因路径上过多或过少的信息素对蚂蚁选择路径产生的影响，避免蚂蚁在搜索路径过程中陷入局部最优。

本文改进算法提高了蚂蚁搜索路径的效率，实验结果表明，改进算法减少了路径的长度，降低了迭代次数，路径更平缓，得到的曲线较为平稳，能够较快地达到稳定值。自适应多启发蚁群算法使得无人机路径规划的综合指标以及平均综合指标均有所降低。

本文将无人机的三维环境投影到二维进行研究，简化了飞行环境，未来还需增加飞行环境的复杂度，以提升算法的实际应用性。

参考文献/References：

[1] 唐立，郝鹏， 张学军. 基于改进蚁群算法的山区无人机路径规划方法[J]. 交通运输系统工程与信息， 2019， 19（1）： 158-164.

TANG Li， HAO Peng， ZHANG Xuejun. An UAV path planning method in mountainous area based on an improved ant colony algorithm[J]. Journal of Transportation Systems Engineering and Information Technology， 2019， 19（1）： 158-164.

[2] CHEN Yongbo， LUO Guanchen， MEI Yuesong， et al. UAV path planning using artificial potential field method updated by optimal control theory[J]. International Journal of Systems Science， 2016， 47（6）： 1407-1420.

[3] 何燕.基于动态加权A*算法的无人机航迹规划[J].河北科技大学学报，2018，39（4）：349-355.

HE Yan.UAV route planning based on improved dynamic weighted A* algorithm[J].Journal of Hebei University of Science and Technology，2018，39（4）：349-355.

[4] 甄然， 张春悦， 矫阳， 等. 基于自适应多态融合蚁群算法的无人机航迹规划[J].河北科技大学学报， 2019， 40（6）： 526-532.

ZHEN Ran， ZHANG Chunyue， JIAO Yang， et al. Research on UAV route planning based on adaptive polymorphic ant colony algorithm[J]. Journal of Hebei University of Science and Technology， 2019， 40（6）： 526-532.

[5] 王琪， 马璐， 邓会亨. 基于遗传算法的UAV自适应航迹规划[J]. 计算机系统应用， 2013， 22（1）： 200-203.

WANG Qi， MA Lu， DENG Huiheng. Adaptive path planning of the UAV based on genetic algorithm[J]. Computer Systems & Applications， 2013， 22（1）： 200-203.

[6] 熊华捷， 蔚保国， 何成龙. 基于改进粒子群算法的UAV航迹规划方法[J]. 计算机测量与控制， 2020， 28（2）： 144-147.

XIONG Huajie， YU Baoguo， HE Chenglong. UAV path planning method based on improved PSO[J]. Computer Measurement & Control， 2020， 28（2）： 144-147.

[7] WANG G G，CHU H E，MIRJALILI S.Three-dimensional path planning for UCAV using an improved bat algorithm[J].Aerospace Science and Technology，2016，49：231-238.

[8] MIAO Hui， TIAN Yuchu. Dynamic robot path planning using an enhanced simulated annealing approach[J]. Applied Mathematics and Computation， 2013， 222： 420-437.

[9] 武晓晶， 许磊， 甄然， 等. 动态步长BI-RRT的无人机航迹规划算法[J]. 河北科技大学学报， 2019， 40（5）： 414-422.

WU Xiaojing， XU Lei， ZHEN Ran， et al. Dynamic step BI-RRT UAV path planning algorithm[J]. Journal of Hebei University of Science and Technology， 2019， 40（5）： 414-422.

[10]赵娟. 启发点引导D*算法扩展的无人机航迹规划策略[J]. 机械设计与制造， 2020（2）： 153-157.

ZHAO Juan.Unmanned air vehicle route planning strategy based on D* algorithm extension guided by inspiration point[J]. Machinery Design & Manufacture， 2020（2）： 153-157.

[11]許江波， 刘琳岚. 基于改进人工鱼群算法的无人机三维航迹规划[J]. 计算机工程与设计， 2019， 40（2）： 540-544.

XU Jiangbo， LIU Linlan. 3D trajectory planning for UAV based on improved artificial fish swarm algorithm[J]. Computer Engineering and Design， 2019， 40（2）： 540-544.

[12]程泽新， 李东生， 高杨. 基于蝗虫算法的无人机三维航迹规划[J]. 飞行力学， 2019， 37（2）： 46-50.

CHENG Zexin， LI Dongsheng， GAO Yang. UAV three-dimensional path planning based on the grasshopper algorithm[J]. Flight Dynamics， 2019， 37（2）： 46-50.

[13]余胜东， 吴洪涛， 马金玉. 应用混沌萤火虫算法的无人机航迹规划[J]. 机械设计与制造， 2018（11）： 113-116.

YU Shengdong， WU Hongtao， MA Jinyu. Path planning for unmanned air vehicle based on chaotic glowworm swarm optimization[J]. Machinery Design & Manufacture， 2018（11）： 113-116.

[14]陆天和， 刘莉， 贺云涛， 等. 多无人机航迹规划算法及关键技术[J]. 战术导弹技术， 2020（1）： 85-90.

LU Tianhe， LIU Li， HE Yuntao， et al. Multi-UAV path planning algorithm and key technology[J]. Tactical Missile Technology， 2020（1）： 85-90.

[15]肖作林，王鹏，冷淑香，等.多无人作战飞机双精度航迹规划技术[J].战术导弹技术，2016（3）：53-57.

XIAO Zuolin，WANG Peng，LENG Shuxiang，et al.Research on the double precision mission planning in multi-UCAV system[J].Tactical Missile Technology，2016（3）：53-57.

[16]朱莉凯，沈朝萍，沈宝国，等.无人机航迹规划群智能优化算法综述[J].数字技术与应用，2019，37（8）：126.

ZHU Likai，SHEN Chaoping，SHEN Baoguo，et al.A survey of intelligent optimization algorithms for UAV route planning group[J].Digital Technology and Application，2019，37（8）：126.

[17]王辉， 胡晓阳. 基于蚁群算法的无人机航迹规划研究[J]. 科技资讯， 2020， 18（10）： 29-30.

[18]刘蓉，杨帆，张衡.基于改进混沌蚁群算法的无人机航路规划[J].指挥信息系统与技术，2018，9（6）：41-48.

LIU Rong，YANG Fan，ZHANG Heng.Path planning for UAV based on improved chaotic ant colony algorithm （CACA）[J].Command Information System and Technology，2018，9（6）：41-48.

[19]张松灿， 普杰信， 司彦娜， 等. 蚁群算法在移动机器人路径规划中的应用综述[J]. 计算机工程与应用， 2020， 56（8）： 10-19.

ZHANG Songcan， PU Jiexin， SI Yanna， et al. Survey on application of ant colony algorithm in path planning of mobile robot[J]. Computer Engineering and Applications， 2020， 56（8）： 10-19.

[20]王琼， 刘美万， 任伟建， 等. 无人机航迹规划常用算法综述[J]. 吉林大学学报（信息科学版）， 2019， 37（1）： 58-67.

WANG Qiong， LIU Meiwan， REN Weijian， et al. Overview of common algorithms for UAV path planning[J]. Journal of Jilin University（Information Science Edition）， 2019， 37（1）： 58-67.

[21]HUANG Liwei， QU Hong， JI Peng， et al. A novel coordinated path planning method using k-degree smoothing for multi-UAVs[J]. Applied Soft Computing， 2016， 48： 182-192.

[22]TAO Jihua， WANG Yinqiu， YANG Huanhuan， et al. Three-dimensional path planning of unmanned aerial vehicle under complicated environment[C]//第28届中国控制与决策会议论文集（下）. [S.l.]：[s.n.]，2016： 1498-1503.

[23]孙功武，苏义鑫，顾轶超， 等. 基于改进蚁群算法的水面无人艇路径规划[J/OL]. 控制与决策.

[2019-11-04]. https：//doi.org/10.13195/j.kzyjc.2019.0839.

SUN Gongwu， SU Yixin， GU Yichao， et al. Path planning for unmanned surface vehicle based on improved ant colony algorithm[J/OL]. Control and Decision. [2019-11-04].https：//doi.org/10.13195/j.kzyjc.2019.0839.

[24]黄心，向煜. 基于改进蚁群算法的无人机航迹规划仿真研究[J]. 城市勘測，2019（1）：83-87.

HUANG Xin， XIANG Yu. Simulation research on UAV route planning based on improved ant colony algorithm[J]. Urban Geotechnical Investigation & Surveying， 2019（1）： 83-87.

[25]李理，李鸿，单宁波.多启发因素改进蚁群算法的路径规划[J].计算机工程与应用，2019，55（5）：219-225.

LI Li，LI Hong，SHAN Ningbo.Path planning based on improved ant colony algorithm with multiple inspired factor[J].Computer Engineering and Applications，2019，55（5）：219-225.

[26]陈劲峰，黄卫华，王肖，等.基于改进蚁群算法的移动机器人路径规划[J].高技术通讯，2020，30（3）：291-297.

CHEN Jinfeng，HUANG Weihua，WANG Xiao，et al.Research on path planning based on an improved ant colony algorithm for mobile robot[J].Chinese High Technology Letters，2020，30（3）：291-297.

[27]KHALED A， FARID K. Mobile robot path planning using an improved ant colony optimization[J]. International Journal of Advanced Robotic Systems， 2018， 15（3）： 1-7.