穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲的FEM-SPH 耦合计算模型*
刘 赛,张伟贵,吕振华
(1. 中国运载火箭技术研究院,北京 100076;2. 清华大学车辆与运载学院,北京 100084;3. 中国科学院空间应用工程与技术中心,北京 100094)
对小口径穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲(透明装甲)的仿真分析普遍采用有限元方法(finite element method,FEM)与光滑粒子流体动力学(smooth particle hydrodynamics,SPH)方法的耦合算法。FEM-SPH 耦合算法可分为两类[1]:一类是固定耦合算法,在初始时刻确定采用有限元方法和SPH 方法的计算区域,并且在后续计算过程中固定不变;另一类是自适应耦合算法,在初始时刻仿真模型全部采用有限元建模,在后续计算过程中将材料大变形或损伤失效的单元自动转化为SPH 粒子,采用SPH 方法计算。对枪弹侵彻这两种复合装甲的仿真分析通常采用固定耦合算法,本文中也采用固定耦合算法进行仿真计算。
SPH 方法是一种无网格数值计算方法,不存在网格畸变问题,而且能够描述物体的边界和模拟材料断裂。SPH 方法对一般固体部件的材料变形和结构响应的计算分析精度仍不及同等尺度的有限元方法。但对于脆性材料的冲击断裂问题,由于有限元方法通常采用网格删除技术模拟断裂,而SPH 方法是采用解除粒子之间的约束来模拟断裂,不存在材料的删除缺失,所以SPH 模型的计算分析精度一般高于同等尺度的有限元模型。因此,对于穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲的仿真分析,一般对脆性材料(陶瓷和无机玻璃)建立SPH 模型,其他部件建立有限元模型,采用FEM-SPH 耦合算法进行仿真分析,得到的脆性材料裂纹、背板变形、弹体剩余质量等与弹道实验的结果较符合[2-3],但弹道极限速度计算值与实验值差异较大。这说明传统FEM-SPH 耦合计算模型的仿真分析精度不高,并不能准确模拟各种弹速下的冲击响应过程。
本文中,利用成熟的显式动力学有限元商业软件,针对小口径穿甲燃烧弹侵彻陶瓷/纤维增强复合材料复合装甲和玻璃复合装甲的仿真分析过程,通过改变传统FEM-SPH 耦合计算模型中穿甲弹弹芯的建模方式和材料模型,提出新型FEM-SPH 耦合计算模型,并研究有限元/粒子尺度和建模尺寸对仿真分析结果的影响规律。
1 陶瓷复合装甲-枪弹系统的新型FEM-SPH 耦合计算模型
陶瓷复合装甲的设计目标是抵抗53 式7.62 mm 穿甲燃烧弹的侵彻,采用两种复合装甲方案,见表1,G 为玻璃纤维增强复合材料,K 为Kevlar 纤维增强复合材料。两种方案的总厚度相同,陶瓷块间距为0.2 mm。方案1 和方案2 的弹道极限速度实验值(着靶速度,下同)分别为778 和764 m/s。A 陶瓷抗冲击能力优于B 陶瓷,但B 陶瓷具有减重优势。

表 1 陶瓷复合装甲组成Table 1 Composition of ceramic composite armors
1.1 新型FEM-SPH 耦合计算模型建模参数
目前陈斌等[2]和卿尚波等[3]建立的FEM-SPH 耦合计算模型中,穿甲燃烧弹弹芯采用FEM 模型和JC(Johnson-Cook)材料模型。孙素杰等[4]和蒋志刚等[5]的试验表明穿甲燃烧弹弹芯在侵彻陶瓷复合装甲的过程中,发生类似脆性材料的碎裂现象,见图1,因此本文中对穿甲燃烧弹弹芯采用SPH 模型代替有限元模型,对弹芯采用适用于陶瓷、无机玻璃等脆性材料的JH2(Johnson-Holmquist-ceramics)材料模型[6]代替JC 材料模型,提出了新型FEM-SPH 耦合计算模型,建模方式等见表2。

图 1 侵彻后收集到的穿甲燃烧弹扭曲变形的被甲和脆性碎裂的弹芯[5]Fig. 1 Twisted jackets and comminuted cores of armor piercing bullets after penetration[5]

表 2 陶瓷复合装甲的新型FEM-SPH 耦合计算模型的建模方式和材料模型Table 2 Modeling methods and material models for the new FEM-SPH model of ceramic composite armors
穿甲燃烧弹的FEM-SPH 耦合计算模型如图2(a)~(b)所示。对铅套和被甲采用六面体单元建模,采用JC 材料模型,屈服应力和失效准则不再赘述,单元失效后即删除,材料模型中屈服应力和失效准则输入参数的具体取值参考文献[7]。陶瓷板是由对边距为50 mm 的正六边形陶瓷块拼接而成。侵彻区陶瓷块的粒子尺度为0.5 mm,非侵彻区陶瓷块的粒子尺度为1 mm。以弹着点在陶瓷块中心的情况为例,建立7 块陶瓷块组成的陶瓷板,如图2(c)所示。
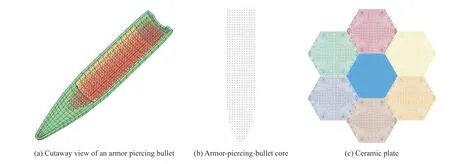
图 2 穿甲燃烧弹的FEM-SPH 耦合计算模型和陶瓷板的SPH 模型Fig. 2 The FEM-SPH model of an armor piercing bullet and the SPH model of a ceramic plate

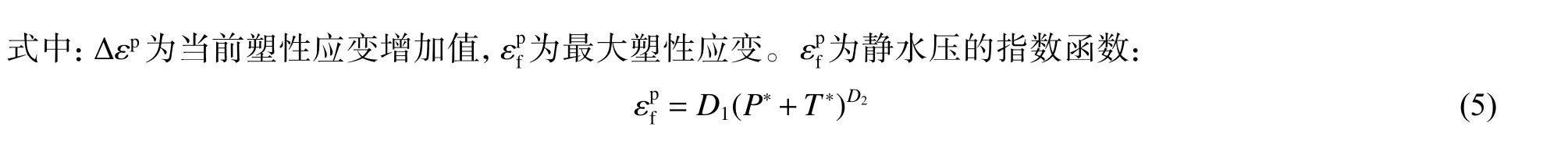
式中:D1、D2为材料模型输入参数。
由式(2)可知,材料完全损伤后不能承受静水拉(即负的静水压),SPH 粒子在静水拉作用下分离,模拟材料脆性碎裂现象,但在静水压下材料由于内摩擦,仍保留一定的屈服应力,弹芯材料模型的主要参数见表3,陶瓷材料模型中式(1)~(5)输入参数的具体取值参考文献[6,8]。

表 3 穿甲燃烧弹弹芯的JH2 材料模型主要参数Table 3 Material constants for the JH2 model of an armor-piercing-bullet core
对靶板中的复合材料采用六面体单元建模,圆形靶板的直径为300 mm,对其采用正交各向异性的连续损伤本构模型[9],考虑了纤维方向拉-剪损伤,纤维面内、面外压缩损伤,基体面内、面外损伤等多种破坏模式,下文举例说明纤维方向拉-剪损伤的破坏模式。定义复合材料单层板面内纤维方向为方向1,垂直于方向1 的面内方向为方向2,面外方向为方向3,方向1 纤维的拉-剪损伤的损伤因子f1的表达式为:

式中: σ1为沿方向1 的应力,〈 〉 表示应力为负时取零, τ12、τ13分别为平面12、13 内的剪应力,S1,t为方向1 纤维拉伸强度,S1,fs为方向1 纤维剪切强度,损伤因子f1增长到1 时,此方向纤维断裂,使该方向纤维拉伸强度和剪切强度降为零,单元并不删除,因为在其他方向可能仍具备承载能力,直到到达预设的临界应变后删除。应变率效应通过应变率效应项来体现,参考式(1)和(2)。复合材料材料模型中弹性模量、剪切模量、强度极限的具体取值参考文献[10-11]。

当粘接的粒子与单元间、单元与单元间的某些界面局部不再满足式(7)或式(8)后,界面此处发生脱粘,转为一般接触。其他非粘接部件间,包括穿甲燃烧弹各部分间、穿甲燃烧弹与靶板间、靶板非粘接部件间,设置一般的自动接触,不考虑摩擦。靶板边界简支,方案1 和方案2 的新型FEM-SPH 耦合计算模型如图3 所示。
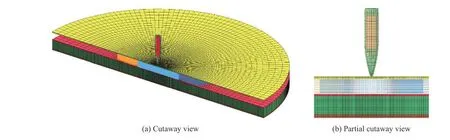
图 3 方案1 和方案2 的新型FEM-SPH 耦合计算模型Fig. 3 The new FEM-SPH model of structure 1 and structure 2
1.2 新型FEM-SPH 耦合计算模型计算结果
着靶速度为750 m/s、侵彻0.15 ms(零时刻为着弹时刻,下同)时,方案1 和方案2 的仿真计算结果见图4,方案1 和方案2 的仿真计算结果均出现层间脱胶的现象,复合材料背板均发生撕裂。陶瓷板和弹芯的等效塑性应变云图见图5,陶瓷锥尺寸基本一致,与B 陶瓷相比,A 陶瓷的裂纹更易形成和扩展,陶瓷碎片飞溅的现象更明显;两种方案仅侵彻区陶瓷出现裂纹,而且径向裂纹的数量基本一致,迎弹面出现约5 条径向裂纹,背面出现约8 条径向裂纹,呈均匀分布;A 陶瓷背面出现一圈周向裂纹,而B 陶瓷没有出现周向裂纹。新型FEM-SPH 耦合计算模型可以有效模拟弹芯碎裂的现象,见图5(i)和(g),方案1和方案2 的弹芯剩余长度基本一致,分别为15 和16 mm。采用二分法获取弹道极限速度计算值,二分法速度间隔取10 m/s(下同),例如着靶速度为750 m/s 时靶板未穿透,着靶速度为760 m/s 时靶板穿透,则弹道极限速度计算值为755 m/s。方案1 和方案2 的弹道极限速度计算值分别为755 和745 m/s,分别低于弹道实验结果3.0%和2.5%。
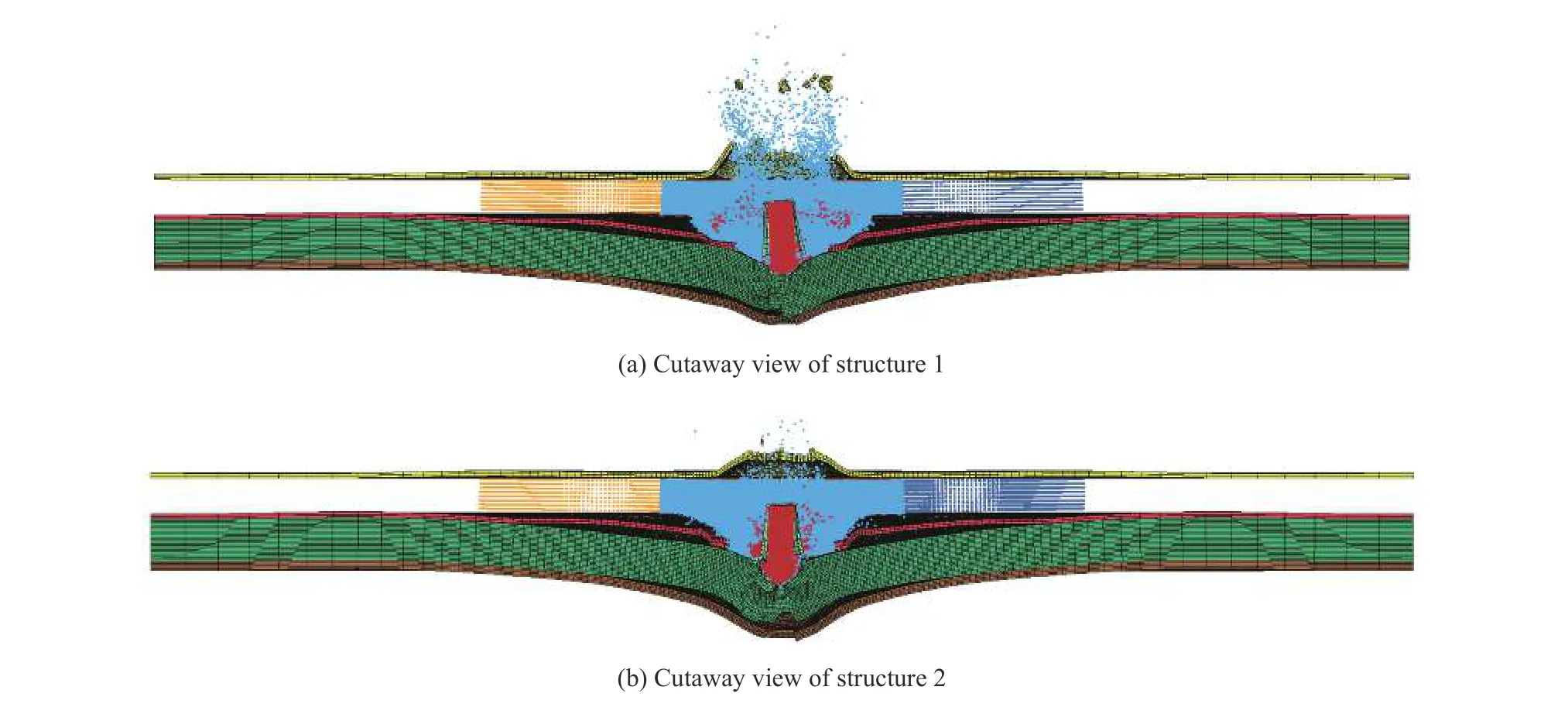
图 4 方案1 和方案2 的数值模拟结果Fig. 4 Simulation results of structure 1 and structure 2
2 陶瓷复合装甲-枪弹系统的有限元计算模型和传统FEM-SPH 耦合计算模型
2.1 有限元计算模型和传统FEM-SPH 耦合计算模型简介
将表2 中全部SPH 粒子替换为相同尺度的六面体单元,弹芯换用JC 材料模型,材料模型中屈服应力和失效准则输入参数的具体取值参考文献[7],得到方案1 的有限元计算模型,见图6(a);将表2 中弹芯的SPH 粒子替换为相同尺度的六面体单元,弹芯换用JC 材料模型,材料模型参数与方案1 的有限元计算模型一致,得到方案1 的传统FEM-SPH 耦合计算模型,见图6(b)。
2.2 有限元计算模型和传统FEM-SPH 耦合计算模型计算结果
采用有限元计算模型和传统FEM-SPH 耦合计算模型得到的弹道极限速度分别为465 和495 m/s。着靶速度为弹道极限速度,侵彻0.20 ms 时的仿真计算结果见图7~9。与图5 中新型FEM-SPH 耦合计算模型的仿真计算结果相比,有限元计算模型侵彻区陶瓷的裂纹分布并不自然,而传统FEM-SPH 耦合计算模型侵彻区陶瓷的裂纹数量较少,两种模型的陶瓷锥尺寸较小,弹芯剩余长度较大(分别为22 和18 mm)。图8(a)表明,有限元计算模型和传统FEM-SPH 耦合计算模型的弹芯单元失效后删除,无法模拟图1 和图5(i)~(g)中弹芯碎裂现象,而弹芯碎片在弹芯与靶板作用过程中起到扩大接触面积、阻碍弹芯侵彻的作用,因此有限元计算模型和传统FEM-SPH 耦合计算模型的弹道极限速度明显低于实验值。
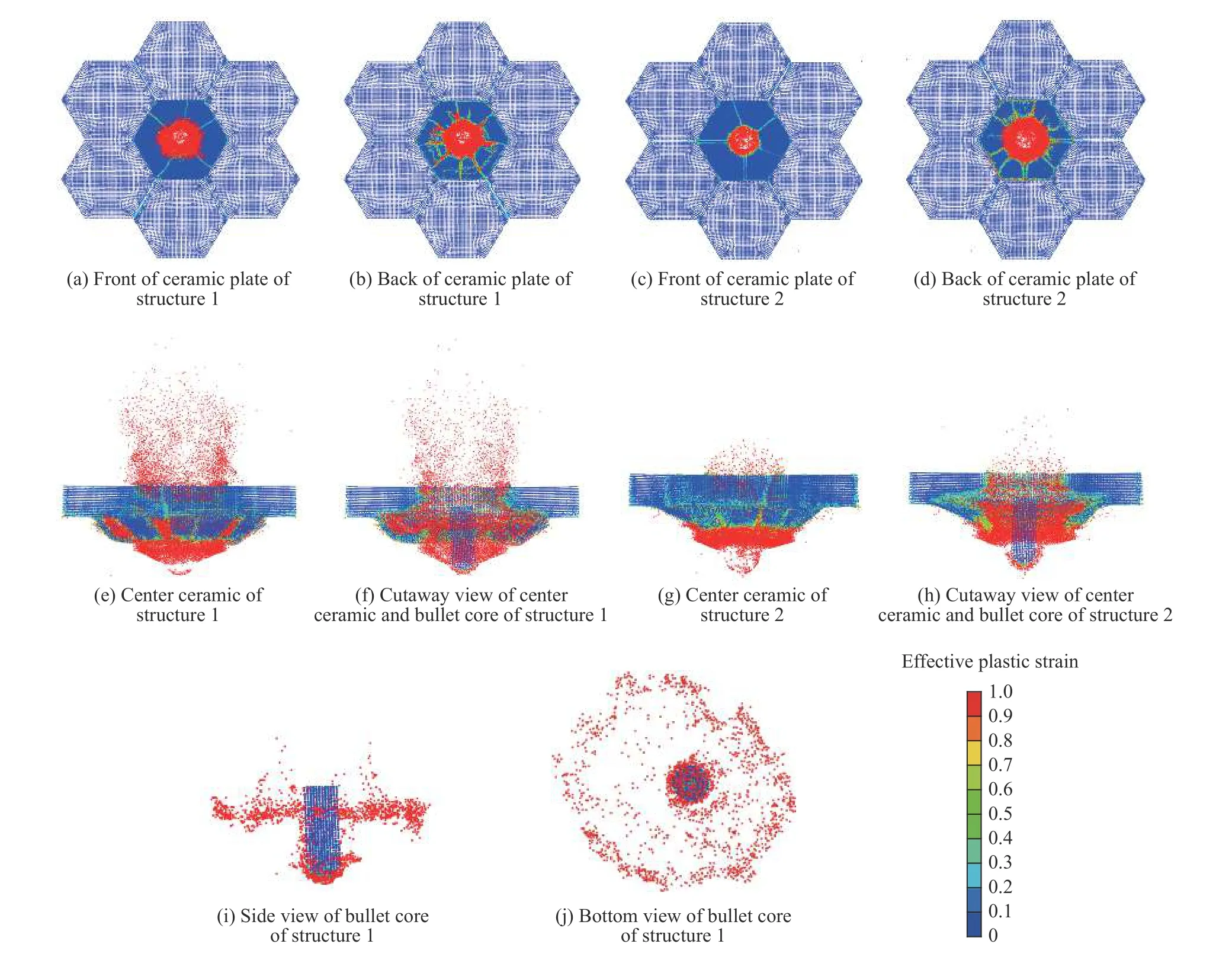
图 5 陶瓷板和弹芯的等效塑性应变云图Fig. 5 Effective-plastic-strain contours of ceramic plates and bullet cores

图 6 方案1 的有限元计算模型和传统FEM-SPH 耦合计算模型Fig. 6 The FEM model and traditional FEM-SPH model of structure 1
方案1 采用不同计算模型得到的弹道极限速度以及5 核并行计算所用的时间见表4,表中OFS为传统FEM-SPH 耦合计算模型,NFS 为新型FEM-SPH 耦合计算模型,NFSA 在NFS 基础上侵彻区陶瓷块SPH 尺度改为1 mm,NFSB 在NFS 基础上侵彻区陶瓷块SPH 尺度改为0.35 mm,NFSC 在NFS 基础上陶瓷块数量改为1,NFSD 在NFS 基础上陶瓷块数量改为19,弹道极限速度以实验值(778 m/s)为归一化标准值,计算时间以NFS 模型的计算时间(6.7 h)为归一化标准值。从表4 可以看出,新型FEM-SPH 耦合计算模型在计算分析精度和计算效率方面均具有较大优势:与传统FEMSPH 耦合计算模型相比,新型FEM-SPH 耦合计算模型的弹道极限速度与实验值的相对偏差由36.4%降低至3.0%,计算时间减少了82.1%。弹芯和陶瓷均为SPH 粒子模型,可大大减少SPH 粒子和有限元耦合计算的计算量,因此减少了计算时间。

图 7 方案1 的有限元模型和传统FEM-SPH 耦合模型的仿真计算结果Fig. 7 Simulation results of structure 1 by FEM and traditional FEM-SPH models
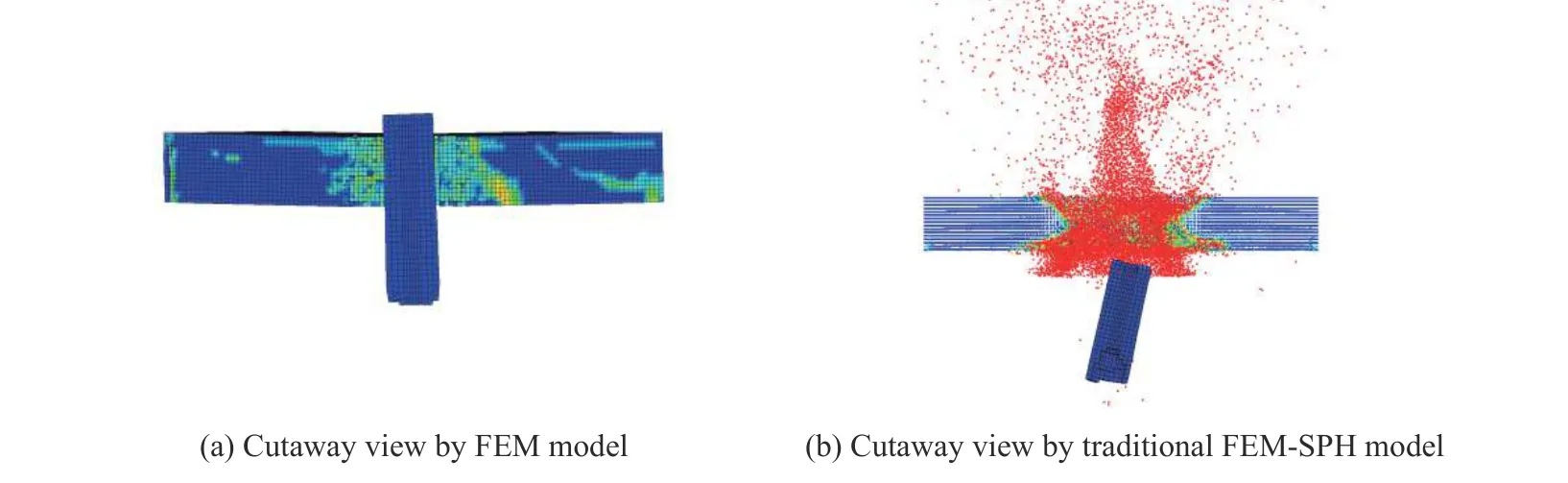
图 8 采用有限元模型和传统FEM-SPH 耦合模型得到的中心陶瓷和弹芯的等效塑性应变云图Fig. 8 Effective-plastic-strain contours of center ceramics and bullet cores simulated by FEM and traditional FEM-SPH models

图 9 有限元模型和传统FEM-SPH 耦合模型的陶瓷板的等效塑性应变云图Fig. 9 Effective-plastic-strain contours of ceramic plates of FEM model and traditional FEM-SPH model

表 4 方案1 采用不同计算模型得到的弹道极限速度以及计算所用的时间Table 4 Ballistic limit velocities of structure 1 by different computational models and the corresponding time used for computation
3 陶瓷复合装甲-枪弹系统的新型FEM-SPH 耦合计算模型的建模参数探讨
改变新型FEM-SPH 耦合计算模型的侵彻区陶瓷块SPH 尺度和陶瓷块数量后,弹道极限速度以及5核并行计算所用的时间见表4。从表4 可以看出,陶瓷块SPH 尺度为0.5 mm、陶瓷块数量为7 块时,弹道极限速度已经达到较高的仿真分析精度。
陶瓷块间距对弹道极限速度计算值的影响如图10 所示。图10 表明,当陶瓷块间距较小时,弹着点位置对弹道极限速度计算值的影响较小,随着陶瓷块间距的增大,弹道极限速度计算值降低,弹着点位置对弹道极限速度计算值的影响增大,此时弹着点位于陶瓷块的接缝处会严重弱化复合装甲的抗弹性能。

图 10 陶瓷块间距对弹道极限速度计算值的影响Fig. 10 Influence of ceramic spacing to computed ballistic limit velocity
4 透明装甲-枪弹系统的新型FEMSPH 耦合计算模型
透明装甲的设计目标是抵抗53 式7.62 mm穿甲燃烧弹的侵彻,采用的装甲方案见表5,G为无机玻璃,PU 为聚氨酯,PC 为聚碳酸酯,总厚度为39 mm,弹道极限速度实验值[12]为584 m/s。
4.1 新型FEM-SPH 耦合计算模型建模参数

表 5 透明装甲组成Table 5 Composition of the transparent armor
采用与上文相同的改进方法建立穿甲燃烧弹侵彻透明装甲的新型FEM-SPH 耦合计算模型,如图11所示,建模方式等见表6。53 式7.62 mm 穿甲燃烧弹的模型和材料参数与1.1 节中的穿甲燃烧弹一致。透明装甲的方形靶板边长为100 mm,无机玻璃的JH2 材料模型中式(1)~(5)输入参数的具体取值参考文献[8],聚氨酯和聚碳酸酯的弹塑性材料模型中屈服应力和失效应变的具体取值参考文献[13-19]。装甲各层材料之间粘接,拉脱强度、实现方式和各部件接触设置与1.1 节中的靶板一致。

图 11 透明装甲的新型FEM-SPH 耦合计算模型Fig. 11 The new FEM-SPH model of the transparent armor

表 6 透明装甲的新型FEM-SPH 耦合计算模型的建模方式和材料模型Table 6 Modeling methods and material models for the new FEM-SPH model of the transparent armor
4.2 新型FEM-SPH 耦合计算模型计算结果
着靶速度为560 m/s,侵彻0.25 ms 时,透明装甲的仿真计算结果见图12~13,弹体部分穿透靶板,无机玻璃碎片飞溅,各层无机玻璃均出现4 条扩展至边界的径向裂纹,呈均匀分布,未发现周向裂纹。弹芯剩余长度为25 mm,弹道极限速度计算值为555 m/s,低于弹道实验结果5.0%。
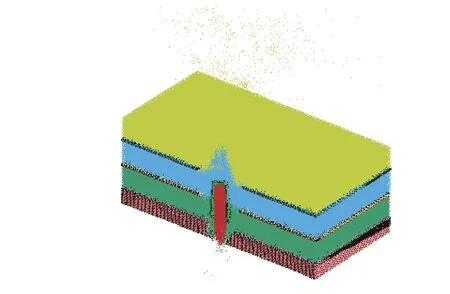
图 12 新型FEM-SPH 耦合计算模型的仿真计算结果剖视图Fig. 12 Cutaway view of simulation result by the new FEM-SPH model

图 13 无机玻璃的等效塑性应变云图Fig. 13 Effective-plastic–strain contours of glasses
5 透明装甲-枪弹系统的有限元计算模型和传统FEM-SPH 耦合计算模型
5.1 有限元计算模型和传统FEM-SPH 耦合计算模型简介
将表6 中全部SPH 粒子替换为相同尺度的六面体单元,弹芯换用JC 材料模型,材料模型参数与2.1 节中的弹芯一致,得到透明装甲的有限元计算模型,见图14(a);将表6 中弹芯的SPH 粒子替换为相同尺度的六面体单元,弹芯换用JC 材料模型,材料模型参数与2.1 节中的弹芯一致,得到透明装甲的传统FEM-SPH 耦合计算模型,见图14(b)。
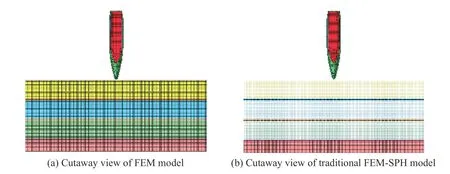
图 14 透明装甲的有限元计算模型和传统FEM-SPH 耦合计算模型Fig. 14 The FEM and traditional FEM-SPH models for the transparent armor
5.2 有限元计算模型和传统FEM-SPH 耦合计算模型计算结果
采用有限元计算模型和传统FEM-SPH 耦合计算模型得到的弹道极限速度分别为415 和505 m/s。着靶速度为弹道极限速度,侵彻0.18 ms 时的仿真计算结果见图15~17。与图13 中新型FEM-SPH 耦合计算模型的仿真计算结果相比,有限元计算模型的无机玻璃裂纹分布并不自然,传统FEM-SPH 耦合计算模型的无机玻璃裂纹数量较少。
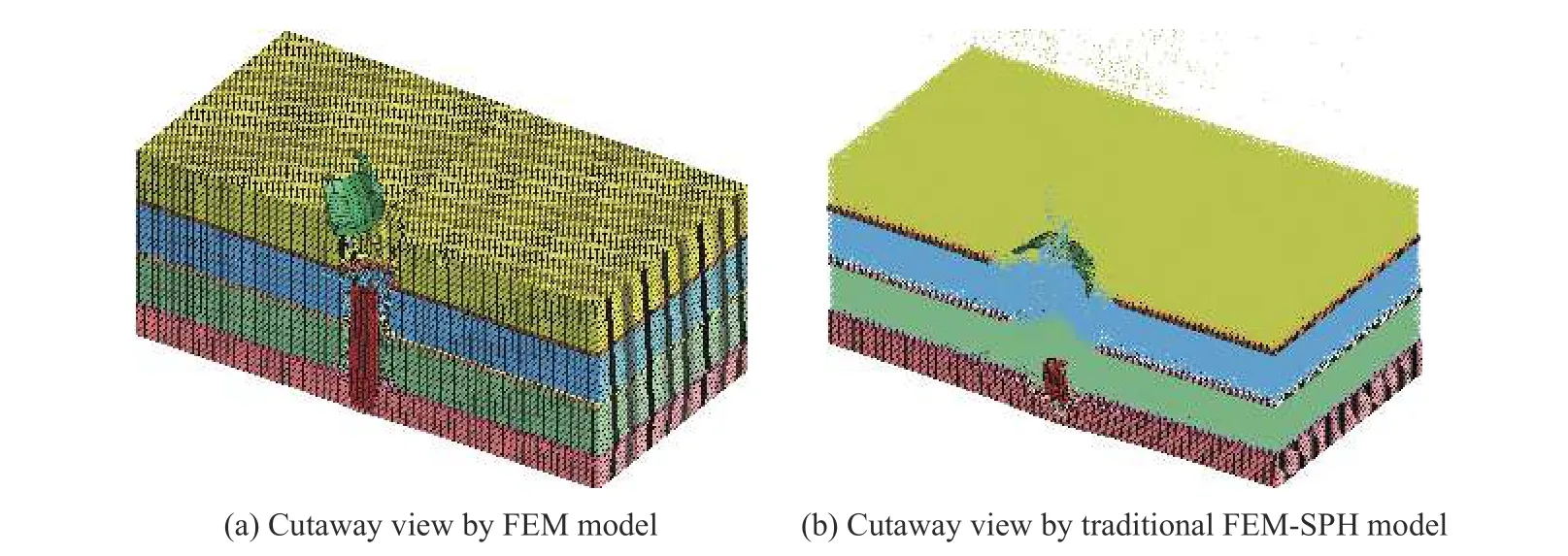
图 15 透明装甲的有限元模型和传统FEM-SPH 耦合模型的仿真计算结果Fig. 15 Simulated results of the transparent armor by the FEM and traditional FEM-SPH models

图 16 采用有限元模型得到的无机玻璃的等效塑性应变云图Fig. 16 Simulated effective-plastic-strain contours of glasses by the FEM model

图 17 采用传统FEM-SPH 耦合模型得到的无机玻璃的等效塑性应变云图Fig. 17 Simulated effective-plastic-strain contours of glasses by the traditional FEM-SPH model
采用不同计算模型得到的弹道极限速度以及7 核并行计算所用的时间见表7,表中OFS 为传统FEM-SPH 耦合计算模型,NFS 为新型FEM-SPH 耦合计算模型,NFSA 在NFS 基础上靶板SPH 和有限元尺度改为0.8 mm,NFSB 在NFS 基础上靶板SPH 和有限元尺度改为0.4 mm,NFSC 在NFS 基础上靶板尺寸改为50 mm×50 mm,NFSD 在NFS 基础上靶板尺寸改为150 mm×150 mm,弹道极限速度以实验值(584 m/s)为归一化标准值,计算时间以NFS 模型的计算时间(14.6 h)为归一化标准值。从表7 可以看出,新型FEM-SPH 耦合计算模型在计算分析精度和计算效率方面均具有一定优势:与传统FEM-SPH 耦合计算模型相比,新型FEM-SPH 耦合计算模型的弹道极限速度与实验值的相对偏差由13.5%降低至5.0%,计算时间减少了81.4%。

表 7 透明装甲采用不同计算模型得到的弹道极限速度以及计算所用的时间Table 7 Ballistic limit velocities of the transparent armor by different computational models and the corresponding time used for computation
6 透明装甲-枪弹系统的新型FEM-SPH 耦合计算模型的建模参数探讨
改变新型FEM-SPH 耦合计算模型的靶板SPH 和有限元尺度、靶板尺寸后,弹道极限速度以及7 核并行计算所用的时间见表7。从表7 可以看出,透明装甲靶板SPH 和有限元尺度为0.6 mm、靶板尺寸为100 mm×100 mm 时,弹道极限速度已经达到较高的仿真分析精度。
7 结 论
本文研究了穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲的FEM-SPH 耦合计算模型的建模方法,基于穿甲燃烧弹弹芯穿甲过程中的脆性碎裂现象,将传统的FEM-SPH 耦合计算模型中穿甲燃烧弹弹芯的有限元模型和JC 材料模型分别替换为SPH 模型和JH2 材料模型,提出了新型FEM-SPH 耦合计算模型,并分析了有限元/粒子尺度、建模尺寸等对仿真分析结果的影响规律,显著提高了穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲的仿真分析精度和计算效率。本文的研究成果具有一般性意义,适用于其他穿甲燃烧弹弹道冲击的仿真分析,有助于提高弹道冲击仿真分析的精度和效率。

