顺层非贯通节理边坡稳定性及破坏模式研究

冯开帅， 姜谙男， 吴洪涛， 焦明伟， 段龙梅

(1.大连海事大学 道路与桥梁工程研究所，辽宁 大连 116026; 2.吉林省交通规划设计院， 吉林 长春 130000)

1 概述

近年以来，随着我国经济的飞速发展，岩土工程数量逐渐增加，其中节理岩质边坡在各类建筑行业中如交通、采矿、土木建筑、水利水电等广泛存在，其稳定性和破坏机制一直受到岩土工程领域的极高关注。岩质边坡的稳定性大部分取决于形成边坡的岩体的物理力学和结构特征，不同的岩体成因和地质构造运动使岩体在岩性和岩体结构上的极大差异性，使边坡具有不一样的潜在破坏模式和稳定性特征[1-2]。岩质边坡中节理的存在，对其岩体强度和破坏模式有较大影响，研究节理问题在岩质边坡工程中不可忽视，这对岩质边坡的安全和防护有着极为重要的作用。

结构面是具有一定方向、延伸较大而厚度较小的二维面状地质界面。其在岩体中的变化极为复杂，结构面的存在使岩体显示构造上不连续性和不均匀性[3-4]。节理是一种重要的地质结构面，它可以分为贯通节理、半贯通节理和非贯通节理，其中非贯通节理较贯通性节理更为复杂且更具有普遍性[5]。在非贯通节理的研究中，李新平[6]等通过数值模拟分析了高陡边坡中节理组的几何分布情况对开挖的影响以及对岩体的影响；周喻[7]等以某铜矿边坡为背景，通过PFC2D软件建立含非贯通节理的顺层边坡模型，研究断续节理内部微观的力学破坏机制问题；卞康[8]等通过PFC2D软件建立含非贯通节理的边坡模型，研究了不同组合形式下的岩桥倾角和节理间距在地震的影响下的边坡破坏模式等问题。阎石[9]等采用FLAC3D软件建立了顺层贯通节理的岩质边坡模型，对其进行稳定性分析，并研究了在结构面倾角、剪切强度、边坡坡率和边坡高度4种因素作用下的边坡稳定性影响规律。金爱兵[10]等通过PFC2D软件建立非贯通节理边坡模型，研究岩桥长度、节理长度、节理倾角3个因素对岩体力学性质的影响。罗福君[11]等以成都至兰州高速某边坡为工程背景，采用FLAC3D中的遍布节理模型分析了顺层节理边坡中节理和岩体参数对安全系数的影响。但目前国内外对岩质非贯通节理边坡的研究还有一定的局限性，在实际工程中，顺层非贯通节理边坡影响因素更为复杂，而对顺层岩质边坡非贯通节理间参数的敏感性分析的文章较少，亟需更为细致的理论方法来合理的评价其稳定性。

本文以吉林某边坡为工程背景，采用Phase有限元软件建立基于Parallel statistical节理网络模型的顺层岩质边坡模型，并运用强度折减法对非贯通节理进行敏感性分析及其破坏规律研究，研究成果可为本类岩质边坡非贯通节理工程提供可靠的参考价值和安全保证。

2 节理有限元与强度折减法

2.1 节理有限元理论

PHASE有限元软件中节理部分的模拟是通过Goodman单元实现。Gooodman是一种无厚度单元，常用于模拟岩体中的软弱结构面。Goodman提出的无厚度四节点八自由度单元(见图1)，1-2和3-4为两片接触面，中间用微小弹簧连接。其中法相刚度系数为kn，切向刚度系数为ks。假设为线弹性接触，则其本构关系表示为：

(1)

式中:σn为节理面法向应力；τs为节理面的切向应力；ωn为节理面的法向位移；ωs为节理面的切向位移。

在外力作用下该单元的接触面处的摩擦强度和变形力学特性是由强度和变形参数来描述的。因此，该单元能较好地模拟节理处的切向力和变形特性。PHASE有限元软件对Goodman单元在受压时接触面两侧相互嵌入的缺陷进行了修正，允许节理部分相互错动，使其产生切向和法向位移，节理部分可出现塑性屈服。

图1 Goodman节理单元Figure 1 Goodman joint unit

2.2 强度折减法

强度折减法是利用Mohr-Coulomb准则，将土体的抗剪强度指标c和φ，用式(2)和式(3)进行折减,将c和φ值同时除以折减系数Fsr,得到一组新的c′和φ′值，反复计算直至达到临界破坏状态，塑性应变发生破坏，坡体发生失稳，在失稳之前的临界折减系数值，即为安全系数Fs。

c′=c/Fsr

(2)

φ′=arctan(tanφ/Fsr)

(3)

式中：c′和φ′为折减之后的强度指标；Fsr为每次计算的折减系数。临界折减系数即为安全系数Fs。

3 模型建立

3.1 工程背景

吉林某公路桩号为K235+900～K235+945段的自然高陡边坡，位于公路左侧，边坡高约45～50m，坡度近直立，坡面凹凸不平，在坡体中下部形成凹腔，坡面岩石主要由强—中风化玄武岩组成，节理裂隙较发育，节理主要产状为226°∠79°、335°∠75°、240°∠35°，节理成顺层断续形状，节理贯通不明显，在重力和风力的长期作用下，岩体中的各结构面不断张开，由闭合向微张、张开、宽张发展，岩体垂直结构面易于张开，与横向结构面贯通之后，被切割的岩体形成潜在崩塌体，并产生掉块、落石，堆于坡脚，其节理裂隙发育如图2所示。

图2 坡面岩体节理裂隙发育

3.2 几何模型建立

本工程数值模拟以吉林省某边坡为研究对象，采用有限元软件Phase建立几何尺寸长为90m，高为50m的高陡边坡，边坡左右边界以及与坡面的交界点处采用水平约束，底部采用固定端约束，坡面为自由边界，初始应力场按自重应力考虑。网格划分为三角形网格,坡面进行了网格加密，如图3所示。

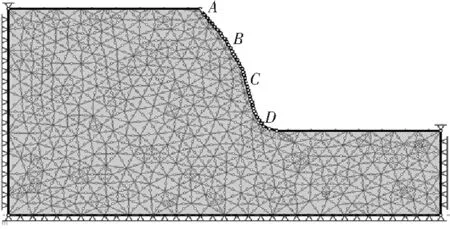
图3 有限元模型网络Figure 3 Finite element model mesh

3.3 Parallel statistical节理模型

Parallel statistical节理网络模型是具有固定的方向、间距和岩桥比例的平行统计节理网络模型，节理倾角、长度、间距和岩桥比例可按泊松分布、均匀分布、指数分布、对数分布生成。根据实际情况，本文选取均匀分布生成断续节理网络模型，如图4所示。

图4 均匀断续节理模型网络Figure 4 Uniform intermittent joint model

3.4 参数设置

边坡和节理本构采用Mohr-Coulomb 屈服准则，节理模型利用PHASE有限元软件中的Parallel statistical节理网络模型，岩体为Ⅳ级岩体，运用降低强度参数的方法模拟节理参数，并参考现场调研情况及勘察资料，岩体参数和节理参数如表1、表2所示。

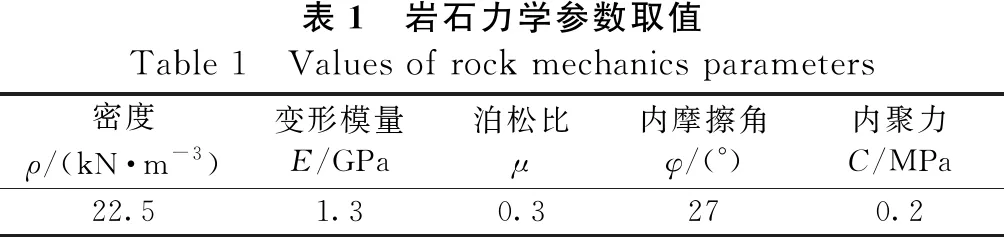
表1 岩石力学参数取值Table 1 Values of rock mechanics parameters密度ρ/(kN·m-3)变形模量E/GPa泊松比μ内摩擦角φ/(°)内聚力C/MPa22.51.30.3270.2

表2 节理力学参数取值Table 2 Joints of rock mechanics parameters抗拉强度σ/kPa内聚力C/kPa内摩擦角φ/(°)切向刚度kn/(MPa·m-1)法向刚度ks/(MPa·m-1)0302310100

4 正交试验设计

正交试验设计是一种研究多因素多水平的试验方法。最主要是选出所有试验中有代表性的点进行试验设计，这些有代表性的点往往是均匀分散的点。这就避免了大量试验工作所带来的困难，方便试验高速有效的进行，是进行多因素多水平计算的最常用优化方案。

4.1 方案设计

根据现场的调研情况和勘察资料选择参数取值范围是：节理倾角0°～80°，节理长度4～6m，节理间距2～4m，岩桥比例L1/L2(如图5所示)0.4～0.8。对这4种因素进行正交试验设计分析，实验有5种水平，具体试验如表3所示，对每种试验进行数值模拟计算，共进行25次数值模拟计算，其结果如表3所示。

图5 岩桥比例Figure 5 Proportion of rock bridge

4.2 计算结果整理分析

用强度折减法计算边坡的安全系数时，把位移突变点作为评价边坡失稳的一种标准。根据现场情况，在边坡上采取4个监测点如图3所示，通过监测坡体内的4个监测点：A点位于坡顶位置，B点位于坡面中上部位置，C点位于坡面中下部位置，D点位于坡脚位置，发现监测点A、B、C、D随着折减系数的增大先比较平稳的增大，到折减系数为1.7附近时，水平位移突然急剧增大，如图6所示，因此其突变点对应的折减系数即为边坡的安全系数。

a.节理倾角与安全系数的关系分析。

为了研究结构面倾角对边坡稳定性的影响，根据现场调研情况，节理采用Parallel statistical节理模型网络，在节理间距为2.5m；节理长度为4.5m；

表3 正交试验Table 3 Orthogonal tests因素倾角/(°)间距/m长度/m岩桥比例安全系数试验10440.41.95试验203.54.50.51.96试验30350.61.98试验402.55.50.71.98试验50260.81.92试验62044.50.61.91试验7203.550.71.72试验82035.50.81.65试验9202.560.41.32试验1020240.51.82试验1140450.81.29试验12403.55.50.41.59试验1340360.51.42试验14402.540.61.78试验154024.50.71.03试验166045.50.51.77试验17603.560.61.69试验1860340.71.85试验19602.54.50.81.75试验2060250.41.73试验2180460.71.97试验22803.540.81.97试验238034.50.41.96试验24802.550.51.96试验258025.50.61.87

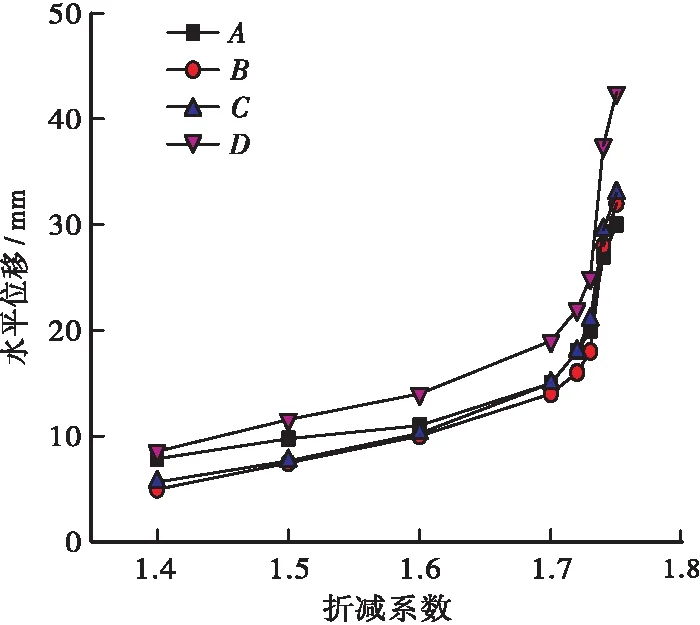
图6 折减系数与水平位移关系图Figure 6 Relationship between reduction coefficient and horizontal displacement

岩桥比例为0.7的情况下，取节理倾角为0°、20°、40°、60°、80°采用强度折减法对顺层非贯通性节理边坡进行安全系数的计算，不同节理倾角的剪切应变云图如图7所示。

其安全系数与节理倾角关系如图8所示。

通过以上分析发现，在节理长度、节理间距、岩桥比例不变的情况下，控制节理倾角由0°到80°渐变，边坡安全系数先减小后增大，在40°时边坡安全系数最小，在0°时边坡安全系数最大；由此认为，边坡在40°角度附近较容易发生塌落掉块现象。研究结果与文献[10]的结论相同，也证明了本文模型的正确性。

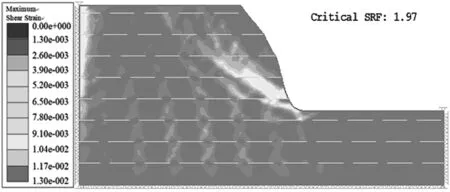
倾角为0°

倾角为20°

倾角为40°

倾角为60°

倾角为80°

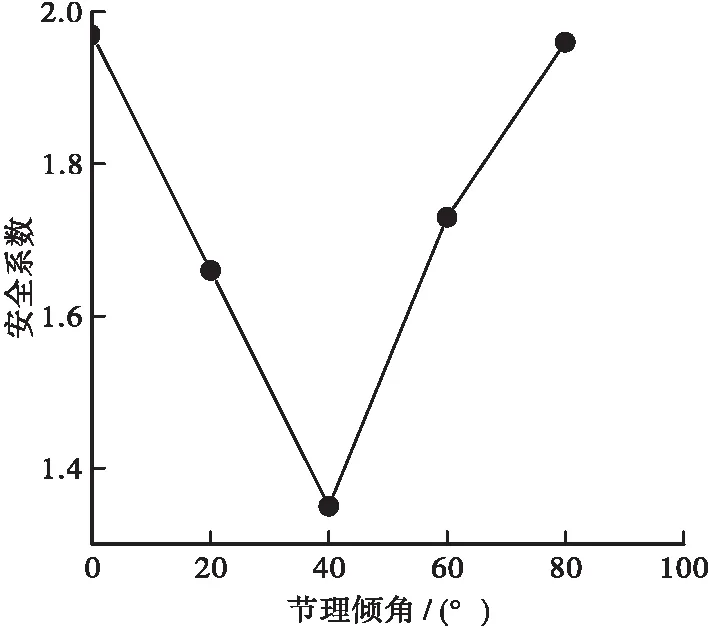
图8 节理倾角与安全系数关系图Figure 8 Relation between joint dip Angle and safety factor

b.节理长度与安全系数的关系分析。

为了研究节理长度对边坡稳定性的影响，并根据现场调研情况，控制节理倾角、间距和岩桥比例不变的情况下，只改变节理长度，对非贯通性节理边坡进行分析，取节理间距为2.5m；节理倾角为40°；岩桥比例为0.7；其节理长度与安全系数关系如图9所示。

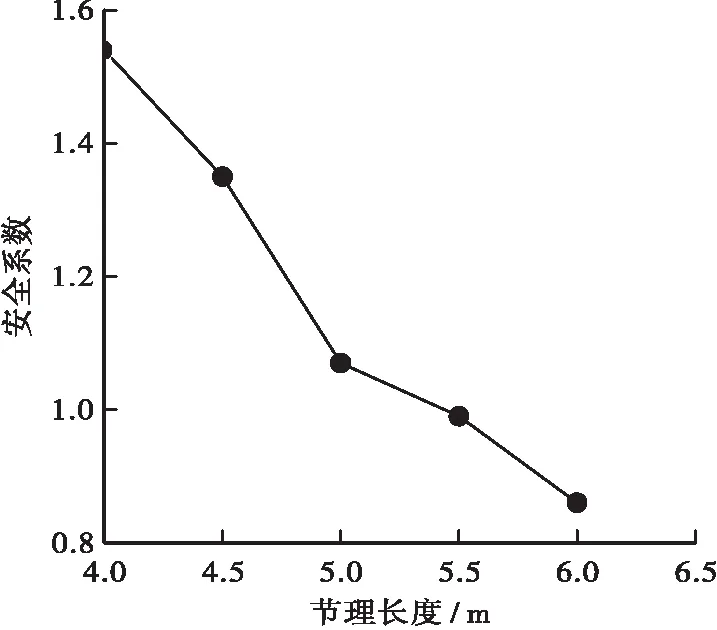
图9 节理长度与安全系数关系图Figure 9 Relationship between joint length and safety factor

从图9中可以看出，控制节理倾角、间距和岩桥比例不变的情况下，只改变节理长度，随着节理长度的增加，安全系数逐渐减小，在该工程中应根据节理长度情况采取相应的措施。

c. 敏感性分析。

为了更好地描述各因素之间的关系，应进行相应的敏感性分析，根据表3中的正交试验设计，利用极差法分析，图10为各因素与安全系数关系图，其中K1、K2、K3、K4、K5为各因素下各水平的综合平均值，表4为极差的计算结果，极差为相应因素各个水平下的极大值和极小值之间的差。

通过图10和表4可以看出节理倾角极差最大，所以节理倾角是影响顺层非贯通节理岩质边坡稳定性的最大因素，当倾角为40°左右时，边坡最容易破坏，其次影响顺层非贯通节理岩质边坡稳定性的是节理长度、节理岩桥比例和节理间距。在极差分析中，极差法虽然简单明了，但是极差分析不能区分试验过程中的因素水平改变和试验误差所造成的数据波动，也不能对因素影响的显著性做出准确的判断。为了弥补直观分析的缺点，还应对试验结果进行方差分析。

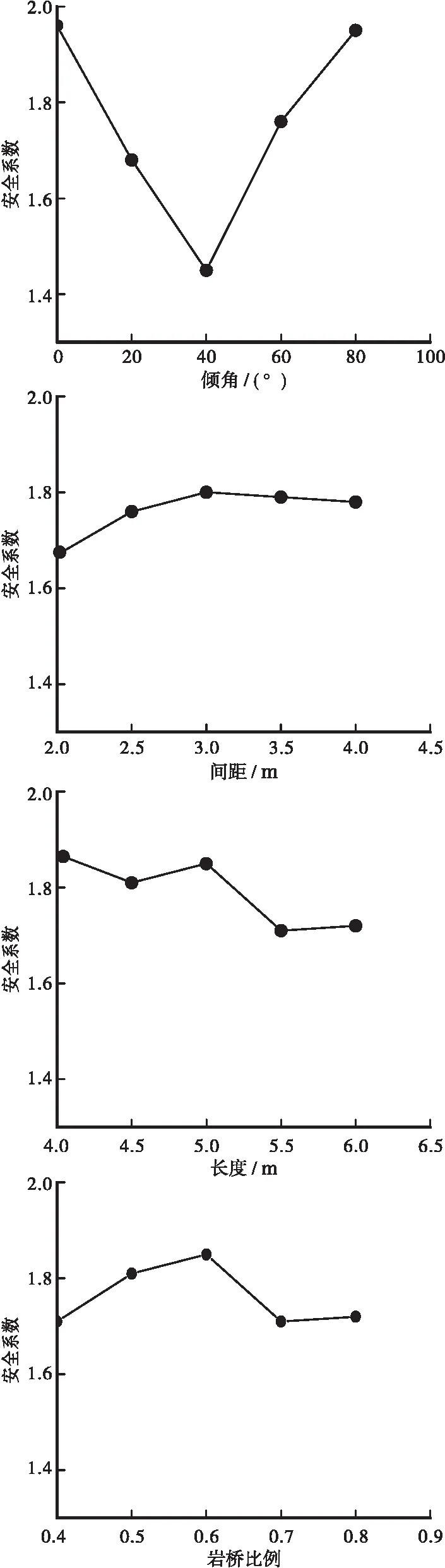
图10 各因素与安全系数关系图Figure 10 The relation diagram of each factor and safety factor

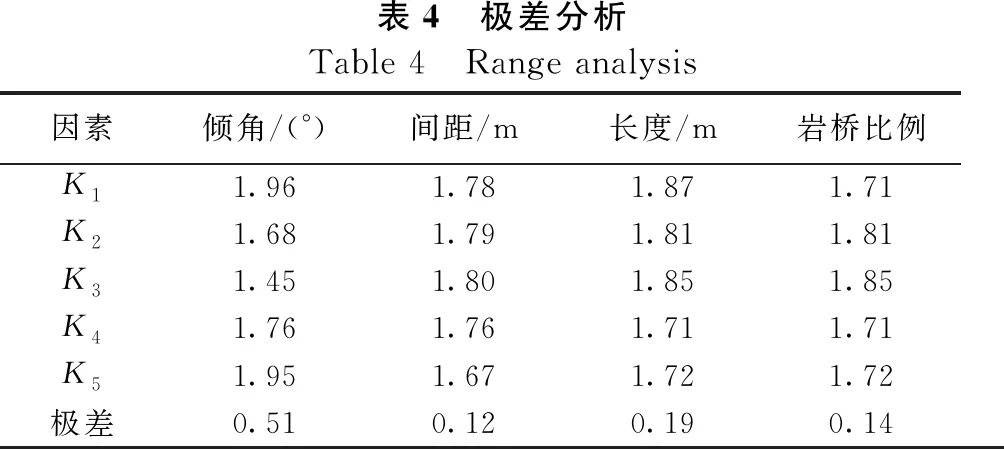
表4 极差分析Table 4 Range analysis因素倾角/(°)间距/m长度/m岩桥比例K11.961.781.871.71K21.681.791.811.81K31.451.801.851.85K41.761.761.711.71K51.951.671.721.72极差0.510.120.190.14

表5为方差分析表，由表5可以看出，对顺层非贯通节理岩质边坡稳定性有极为显著影响的是节理倾角，对边坡稳定性有显著影响的是节理长度，其次是节理岩桥比例和节理间距。当节理倾角为40°左右时，边坡最容易破坏。

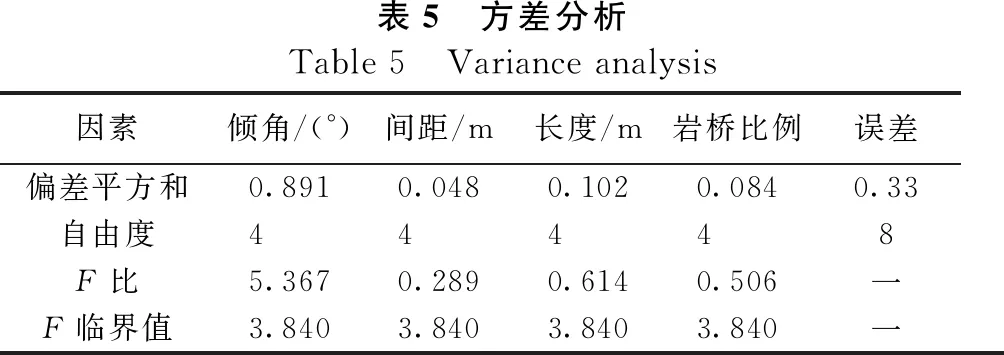
表5 方差分析Table 5 Variance analysis因素倾角/(°)间距/m长度/m岩桥比例误差偏差平方和0.8910.0480.1020.0840.33自由度44448F比5.3670.2890.6140.506一F临界值3.8403.8403.8403.840一

5 破坏模式分析

为了研究非贯通性节理与贯通性节理的破坏模式并根据工程实际情况，对节理倾角为40°的非贯通性节理和贯通性节理边坡进行分析，非贯通性节理选取节理倾角为40°，节理间距为2.5m，节理长度为4.5m，岩桥比例为0.7；贯通性节理选取节理倾角为40°，节理间距为2.5m。两种破坏模式对比如图11所示。

非贯通节理

贯通节理

通过图11可以看出，在节理间距、长度和岩桥比例不变的情况下顺层边坡倾角为40°时非贯通节理和贯通节理破坏模式不同，非贯通节理在节理两端易产生应力集中，节理裂隙发展路径先由坡脚非贯通节理端部产生，再逐渐发育到相邻非贯通节理，并向坡体上部发展，最终较多节理裂隙相连导致边坡发生沿节理面破坏，安全系数为1.35。而贯通节理的节理裂隙发展路径是由坡脚产生，并沿节理面直线上升到坡顶发生破坏，破坏较为明显，且安全系数较低，为0.77，于是可知，贯通节理较非贯通节理更易破坏，工程中应对不同破坏模式做好相应的措施以防止危险发生。

6 结论

含有非贯通性节理的岩质边坡在边坡工程中广泛存在，破坏性大，不易控制，对施工影响颇大，其稳定性和安全性日益受到岩土工程的广泛关注。本文主要通过研究非贯通性节理的稳定性和破坏模式得出以下结论:

a. 利用PHASE有限元软件，并采用了Parallel statistical节理模型，较好地模拟了工程实际，为工程提供了一定的参考价值。

b. 通过正交试验，并采用极差和方差法分析可以看出，对顺层非贯通节理边坡稳定性影响最显著的因素是节理倾角，影响边坡稳定性的因素排序依次是节理倾角、节理长度、岩桥比例和节理间距，节理倾角过小，应立即采取有效措施进行防护，以避免对安全造成威胁。

c. 通过对比非贯通节理和贯通节理的破坏模式可知，非贯通节理的破坏一般先从坡脚开始，然后发生沿节理的剪切破坏，之后节理之间相互贯通导致边坡失稳；贯通节理的破坏一般也由坡脚先破坏，之后沿节理面发生整体的滑移破坏，导致边坡失稳。贯通节理岩质边坡破坏较剧烈，破坏性强。这对该工程支护位置的选择以及采取何种措施有一定的参考意义。