聚合物锂电池P2D模型的参数辨识方法

肖 席，王建立，阮 喻

（陆军工程大学通信士官学校，重庆 400035）

0 引 言

聚合物锂电池工作原理与普通锂离子电池相同，主要区别是其正极采用高分子聚合物或无机化合物，电解质采用胶态或固态的高分子电解质或有机电解液。此外，聚合物锂电池一般为软包电池，且外形设置比较多样。锂离子电池结构如图1所示。

图1 锂离子电池结构

伪二维模型（Pseudo 2 Dimensional Model，P2D模型）是Newman等人利用电压和电流等参数结合微分方程建立的电化学模型，其主要以电池结构和电池内部的化学反应行为为依据，模型精度较高，能较大还原电池内部的物理化学过程[1]。

物理化学过程包括电极材料活性粒子间的固相扩散过程、锂离子在电解液中的液相扩散、电极表面活性粒子处的电化学反应以及锂离子在电解质迁徙和在电极中的移动。其中，固相和液相扩散均遵循Fick第二扩散定律，电化学反应遵循Bulter-Volmer方程。Gregory等进一步解析为电极和电解液的电荷守恒方程和质量守恒方程、电极电解液之间锂移动速率方程[2]。由于模型包括十多个微分方程，计算复杂，实际使用受限，因此需对模型简化分析并明确各极化过程参数的辨识方法。

1 聚合物电池及实验设备

聚合物方形电池的标称容量为2 000 mAh，标称电压为3.6 V，截止电压为4.2 V，重40 g。实验设备包括LX-PCBT-100-8D力兴电池测试仪、恒温箱（勤卓环试-70～+150 ℃）、计算机以及YR1030电池内阻测试仪。

2 各过程参数辨识方法

2.1 欧姆极化过程参数辨识

应用YR1030电池内阻测试仪，常温25 ℃下接电池的两极，直接测得欧姆内阻23.1 mΩ，欧姆极化电势为：

式中，ηohm为欧姆极化过电势；Rohm为实测欧姆内阻。

2.2 固相扩散过程参数辨识

此过程主要是辨识电极的基本参数y0，x0，D1，D2，其中，y0和x0分别为正极、负极初始嵌锂浓度；D1，D2为浓度变化范围。

2.2.1 基本计算式

小倍率放电时，近似认为测得的端电压为理想电动势，即：

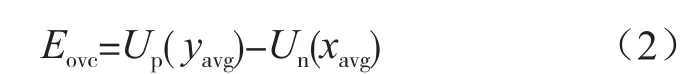
式中，Eovc为理想电动势；Up(yavg)、Un(xavg)分别为正负极电势。

由于电流较小，忽略极化影响，近似认为：

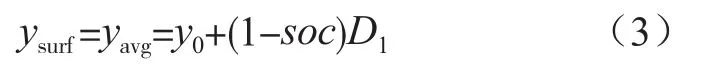
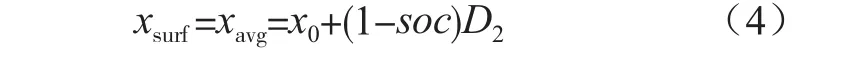
式中，ysurf和yavg分别为表面嵌锂浓度和平均嵌锂浓度；y0，x0，D1，D2分别为初始嵌锂浓度及变化范围；soc为荷电状态。

2.2.2 小倍率放电实验

设计在小倍率0.02 C（40 mA）倍率下放电工况，此时可忽略极化过电势，将式（3）和式（4）代入式（2）进行求解。小电流放电测试结果如图2所示。

图2 0.02 C放电电压-容量曲线图

由于正负极电极容量Up(ysurf)和Un(xsurf)对某一特定电极来说是已知的函数，据此可推导Eovc和(x0,y0,D1,D2,soc)关系，与实测理想电势变化曲线对比并利用最小二乘拟合，可求解(x0,y0,D1,D2,soc)[3]。

2.2.3 结果分析

由图2中0.02C放电实验数据，可在Matlab中利用最小二乘拟合描绘Eovc-soc曲线，如图3所示。多次设定初始值并作各阶拟合后确定选择3次多项拟合以保证曲线与实测值的吻合程度（本文拟合时均方根误差RMSE=13.22），此时最小二乘法求解得到x0=0.54，y0=0.01，D1=0.05，D2=0.1。

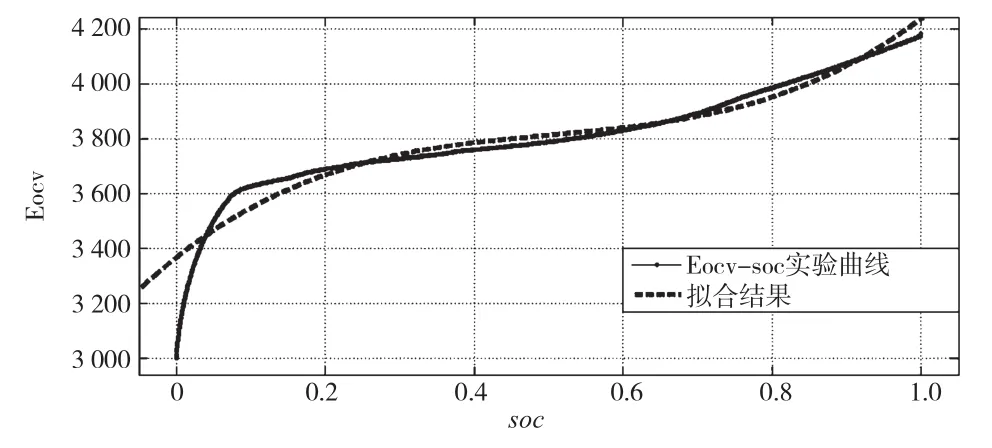
图3 利用最小二乘拟合描绘的Eove-soc曲线

2.3 反应极化过程参数辨识

2.3.1 反应极化过电势的基本计算式

反应极化过电势的基本计算式为：

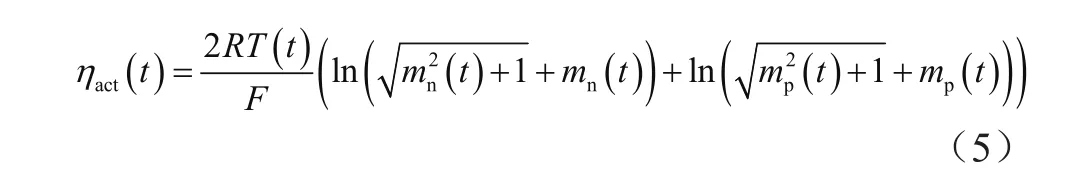
式中，ηact(t)为反应极化过电势；Qp，Qn为正负电级容量；c0为电解液初始锂离子浓度；R为理想气体常数，单位为J·mol-1·K-1；T为热力学温度，单位为K；mp，mn为中间变量；F为法拉第常数，单位为C·mol-1；Pact为反应极化常数，单位为m-1.5·mol0.5·s，且Pact越大，表征电化学反应过程越难，反应速率越低。

2.3.2 外加激励电流的参数辨识方法

设计外部激励电流循环进行电池充放电，根据各步骤电压突变和欧姆过电势可求解反应极化过电势ηact(t)，进而求解各反应极化过程参数。设计激励电流工况如表1所示。

先在恒温箱中静置2 h，再进行循环1。表1中“0”表中指静置状态，且每个静置过程持续10 min。分别记录循环2～8第一步的电流值I（用于计算欧姆过电势）、电压值ΔU1～ΔU7，ΔUi表示循环i+1开始时施加电流瞬间的电压突变。

电压下降过程中，图5电流显示为正，实际为负值（按照设计工况对照即可）。电流施加瞬间，记录电压突变ΔUi，减去计算的欧姆极化过电势，得反应极化过电势，即ηact=ΔUi-ηohm。表2为激励电流工况下电压及过电势实验结果。

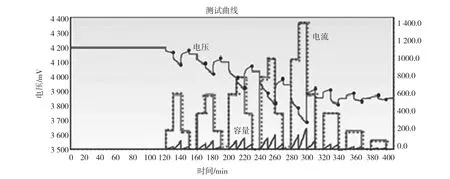
图5 电流激励工况测试

表1 设计激励电流工况及步骤

表2 激励电流工况下电压及过电势实验结果

先计算式（3）和式（4）中平均嵌锂浓度，代入式（5）即可求解Pact。辨识结果为Pact=103 586 m-1.5·mol0.5·s。

2.3.3 结果分析

反应极化在施加电流瞬间即完成，可根据瞬时电压突变分离欧姆过电势，从而解耦出极化过电势及反应极化系数。由式（5）知，Pact受温度影响较大，该处仅选取的温度为常温25 ℃实验为例求解。

2.4 液相扩散参数辨识

2.4.1 基本求解计算式

液相扩散极化过电势为：

恒流时：

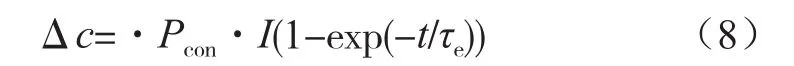
式中，ηcon为液相扩散极化电势；Pcon为液相扩散比例系数，单位为mol·m-3·A-1；τe为液相扩散时间常数，单位为s；Δc为电极电解液交界面液相锂离子浓度变化值，单位为mol·m-3。

选取研究激励工况中21个恒流充放电截止点均达到稳态[4]。如图5所示黑色圆点标注为扩散平衡的截止点，各截止点端电压计算满足：

式中，yavg、xavg在固相扩散中已求解，直接代入，此时ysurf1=yavg+Δy，xsurf1=xavg-Δy。

各截止点：

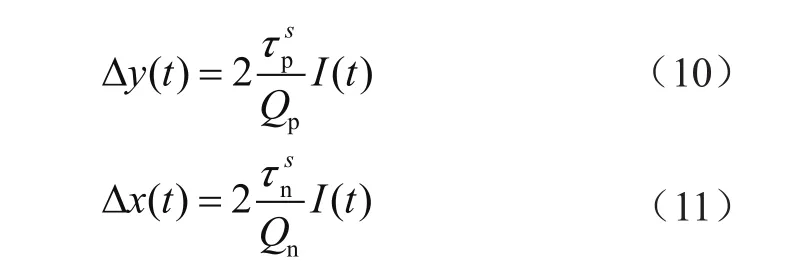
2.4.2 求解过程

基于不同截止点建立的方程，最小二乘拟合求式（9）中未知项Δy，Δx，ηcon。

根据式（10）和式（11）在所测温度求出的结果取平均值，求得τsp=394.56 s，τs

n=143.22 s。

Δc的求解，根据式（6）。

Pcon的求解，由式（8），Δc(稳态)=Pcon·I(t)，其中Δc(稳态)为某恒流维持t=10 min时，即液相扩散进入稳态，求得Pcon=48.33 mol·m-3·A-1。

τe的求解，由式（7），将Pcon和Δc代入反向求解，τe=50.87 s。

2.4.3 结果分析

由稳态时间截止点的电压和电流值，结合端电压计算式（9），最小二乘可解耦液相扩散相关参数。该过程需要注意，扩散平衡时间预留10 min，近似认为已达到稳态；温度对扩散过程影响较大，温度影响需进一步在其他温度下实验并进行参数辨识。

3 结 论

通过0.02 C小电流放电辨识固相扩散过程参数，各参数最小二乘3阶拟合误差较小。

交流激励实验可辨识反应极化和液相扩散过程参数，反应极化选取电流突变时的电流电压值进行分析辨识，液相扩散选择各过程持续10 min即极化进入稳态的电压、电流值结合固相扩散过程已辨识出的结果进行参数辨识。

各极化过程参数与温度相关，需改进并修正建立温度相关模型以提高本方法的温度适用性。