基于粒子群优化算法的无功和电压控制及仿真
李旭炯
(兰州资源环境职业技术学院,甘肃 兰州 730021)
0 引 言
无功功率和电压控制(Reactive Power and Voltage Control,RPVC)是考虑负荷变化和无功功率均衡来保持电力系统的电压。目前, RPVC是通过运行点的潮流灵敏度分析,利用有限执行时间和来自实际目标系统的可用数据来实现。降低发电成本是电力企业关心的问题之一,因此,RPVC需要一种最优控制以使传输损耗最小化,而不仅是简单的潮流灵敏度分析。
RPVC可以建模成为 混合整数非线性优化问题(Mixed-integer Nonlinear Optimization Problem,MINLP),其中包括连续变量,如自动电压调制器(Automatic Voltage Regulator,AVR)操作值,也包括离散变量,如变压器的有载分接开关位置(Tap Positions of on-load Tap Changer,OLTC),及一定数量的无功功率补偿装置(Reactive Power Compensation Equipment,RPCE),如静态电容器(Static Condenser,SC)和并联电抗器(Shunt Reactor,ShR)。以往对RPVC的处理方法主要是采取模糊算法、专家系统、数学规划及敏感性分析方法等。本文将RPVC建模成为一个具有连续和离散状态变量的MINLP,引入PSO,并确定了具有连续和离散控制变量的控制方法[1]。
粒子群优化算法(Particle Swarm Optimization,PSO)是一种进化计算技术[2]。本文所述方法既能处理连续状态变量,也可处理离散状态变量,因此可将RPVC建模成为MINLP。当然,已研发并用于MINLP方法,如分解法(GBD)和OA/ER,这些方法将整个问题分解成若干子问题。相反,PSO可从整体上更有效地解决MINLP。此外,RPVC需要各种难以用数学方法处理的约束,而PSO很容易地处理这些约束。
本文阐述了利用PSO将RPVC建模成为MINLP,通过与实际系统模型的主动禁忌搜索(Reactive Tabu Search,RTS)和枚举法的比较,证明了其可行性,并取得了预期结果。
1 RPVC公式化
1.1 问题公式化
电力系统中RPVC公式化为:
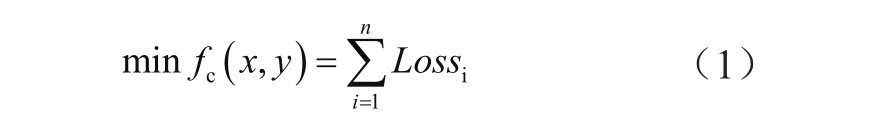
式中,n为分支的数量;x为连续变量;y为离散变量;Lossi为支路i上的功率损耗。
利用连续变量(AVR操作值)和离散变量(OLTC与RPCE),可得出RPVC中功率损耗。潮流计算结果可用来校验电压和潮流约束,若违反约束则加罚值。实际应用中RPVC应考虑电压安全评估。
1.2 状态变量
无功功率和电压控制中使用如下控制设备:自动电压调制器、变压器的有载分接开关位置及一定数量的无功功率补偿装置。
其中,AVR操作值(连续变量)、OLTC(离散变量)、RPCE(离散变量)3个状态变量在负荷潮流计算中处理如下:
AVR操作值——电压标准值,OLTC——每个抽头位置的抽头比率,RPCE——相应的电纳值。
2 PSO在MINLP中的扩展
PSO是对简化社会模型的仿真而发展起来的,其搜索过程可描述为:一群粒子优化某一个特定的目标函数,且每个粒子都知道各自的最佳值(体极值)和坐标,此外每个粒子也知道其在组群中的最佳值(全局极值)。利用当前速度及与体极值与全局极值的距离,可得出每个粒子的修正速度,公式为:
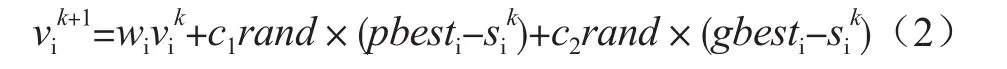
其中,vik为迭代k时粒子i的速度;vik+1为粒子i的修正速度;rand为[0,1]的随机数;sik为迭代k时粒子i的当前位置;pbesti为粒子i的体极值;gbesti为粒子i的全局极值;wi为粒子i的速度权函数;ci为每一项的权重系数。
利用式(2),可算出一个逐渐接近体极值和全局极值的速度。对当前位置修正如下:

离散变量只需稍加修改,就可用式(2)和式(3)处理,连续变量和离散变量都可在算法中处理。
3 利用PSO的RPVC方程
3.1 状态变量的处理
PSO中, 可对每个变量做如下处理。
(1)AVR:初始操作值在电压规范值的上、下界间随机产生,在搜索过程中确定的范围内修正。
(2)OLTC:抽头位置最初在最小至最大间随机产生,搜索过程中在现有位置之间修正,然后计算相应的变压器阻抗,进行潮流计算[3]。
(3)RPCE:数量从0到变电站原有设备的数量,搜索过程中在0和现有设备数量之间修正。
3.2 基于PSO的RPVC算法
将RPVC建模成为MINLP的PSO步骤如下:
步骤一,利用上述状态变量随机生成粒子的初始搜索点。
步骤二,每个粒子搜索点损耗由潮流计算得到,如违反约束,在损失基础上增加惩罚。
步骤三,将体极值设为每个初始搜索点。将体极值中的初始最优评估值(损失加惩罚)设为全局极值。
步骤四,计算新速度使用式(2),连续变量采用连续方程,离散变量采用离散方程。
步 骤五,计算新搜索点使用式(3),连续变量采用连续方程,离散变量采用离散方程。
步骤六,计算新搜索点和估计值的损耗。
步骤七,如每个粒子的估算值优于之前的值,则将这个值设为体极值;如最优体极值优于全局极值,将此值设为全局极值,存储所有全局极值作为最终控制策略的候选值。
步骤八,如迭代数达到最大值则修正,否则回到步骤四。
如违反电压和潮流约束,则对最大和最小边界的绝对违反值加权,并将其作为惩罚项添加到目标函数中。通过预模拟,确定最大迭代次数。如上所述,即使对于大规模问题,PSO的迭代次数也不超过百次。
4 数值实例
将PSO应用于改进型IEEE14节点系统,与RTS和枚举法相比。
4.1 仿真条件
图1为一个改进型的IEEE14节点系统,表1为运行条件,控制变量如下:(1)节点2、3、6和8处,发电机和同步补偿器的连续AVR运行值为0.9~1.1 p.u.;(2)节点4-7、4-9和5-6之间,变压器抽头位置为离散,假设变压器有20个抽头位置;(3)节点9和14,SC的离散值为假设每个节点有3个0.06 p.u.的 SC。

图1 改进型的IEEE14节点系统

表1 IEEE14节点系统的运行条件
该方法试图为运行条件生成最优控制,原系统的损耗为0.134 9 p.u.。在仿真中,比较PSO、RTS和枚举法,根据预模拟,仿真采用如下参数:
式(2)中函数的系数w设为如下方程[4]:
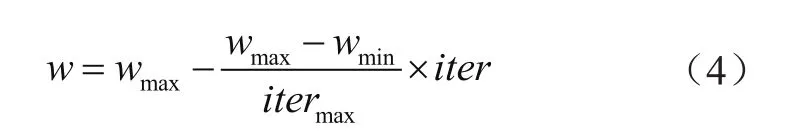
式中,wmax=0.9,wmax=0.4,itermax为最大迭代数;iter为当前迭代次数。
式(2)中,c1,c2设为2.0,根据预模拟,wmax,wmin,设为 0.9和0.4。PSO中粒子数为10,RTS参数通过预模拟确定。仿真中,RTS初始仿真步长为10,仿真步长增减率为0.2。将结果与300次搜索迭代比较,RTS和枚举法采用数字化AVR操作值,间隔为0.01 p.u.,在500 kV系统中间隔为5 kV。组合优化公式大约有109个组合,系统采用C语言开发,所有仿真均采用EWS进行。
4.2 仿真结果
表2给出了PSO、RTS和枚举法的最优结果,表3给出了PSO和RTS结果的损失值和计算时间[4]。RTS的最优结果和枚举法相似,但由PSO得到的损耗小于最优值,同时一个分接开关对应的结果也不相同。当RPVC以能效比衡量时,只搜索离散值的解,同时目标函数在离散区间之间的形状也是值得关注的。因此作为MINLP和能效比的最优解决方法不同。结果表明,将RPVC作为MINLP来建立方程更有效。PSO损耗比RTS少15%,而计算时间却快15%。仿真中,式(4)中wmax,wmin及式(2)中ci都发生了改变,对每种情况,经过100次搜索迭代,结果显示wmax,wmin为0.9和0.4,ci最优值为1.5。

表2 IEEE14节点系统的最优控制
表2中,AVR2为节点2的AVR操作值,单位为p.u.;Tap4-7为节点4和7之间的分接头比例;SC9为节点9的电纳,单位为p.u.。
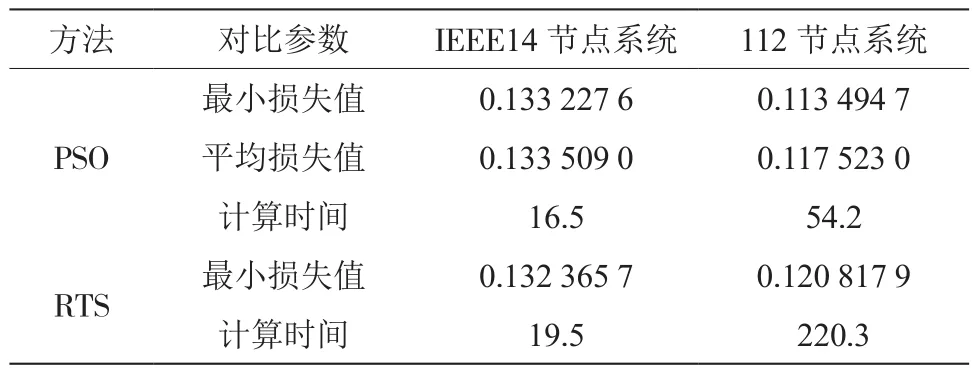
表3 PSO和RTS的计算结果对比
表3中,损失值为有功功率损失,单位为p.u.;计算时间为平均计算时间,单位为s。
5 结 论
本文阐述了电力系统中针对RPVC的PSO,该方法将 RPVC建模成为MINLP,用连续和离散控制变量决定控制策略,如AVR操作值、OLTC及RPCE,在实际电力系统中验证了可行性,取得了良好效果。

