智能汽车换道轨迹规划曲线研究

张甫城，胡敏，江书真

（长安大学汽车学院，陕西 西安 710064）

引言

在高速公路上，换道是最常见的驾驶行为之一。随着自动驾驶技术的发展，对换道轨迹规划的研究的方法也很多，其中包括人工势场法、曲线拟合方法和搜索算法等，换道车辆的轨迹规划[1]直接决定了自动驾驶汽车能够高效、安全的完成换道任务，因此对轨迹规划曲线的就显得特别具有意义。

1 人工势场法

通过人工建立势场，把障碍物设置成为斥力，把目标设置成引力，通过这种力的叠加的方法，对车辆的运动轨迹进行规划。

引力场：

斥力场：

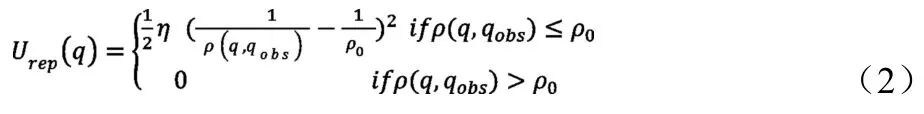
其中ξ和η是尺度因子，ρ（q，qgoal）表示物体当前状态与目标的距离，ρ（q，qobs）表示物体与障碍物之间的距离，ρ0代表每个障碍物能产生影响的半径范围。

用人工势场法去研究轨迹规划，简单实用，同时其具有实时性。但是，在目标点距离比较远的时候，引力的作用就会非常大，物体的路径可能会碰到障碍物，同时当目标点附近存在障碍物的时候，会导致斥力非常大，这样容易影响到达最终的目标点。

2 曲线拟合法

2.1 等速偏移模型

等速偏移模型包括三个直线阶段A1A2、A2A3、A3A4，车道宽Yab，变道纵向距离为Xab，由于模型的轨迹全部由直线组成，导致在每一个拐点处形成了突变，一阶导不连续，所以等速偏移作为换道轨迹无法满足实际的变道情况。

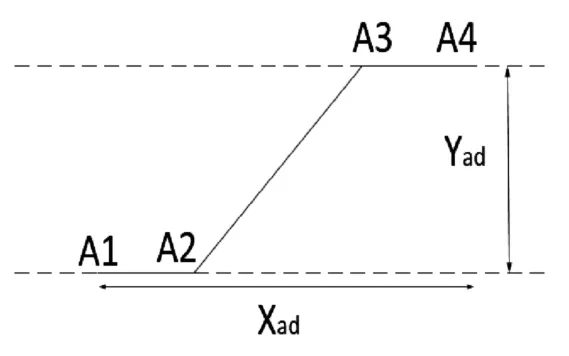
图1 等速偏移模型

2.2 圆弧变道曲线模型

圆弧轨道模型是由两端圆弧和一段直线所组成B1B2、B3B4、B2B3，车道宽Yab，变道纵向距离为Xab，直线部分二阶导为零，圆弧上每点二阶导为定值，但是在B2、B3两点处也存在曲率的突变，在实际的换道过程中轨迹曲线无法满足圆弧变道模型。

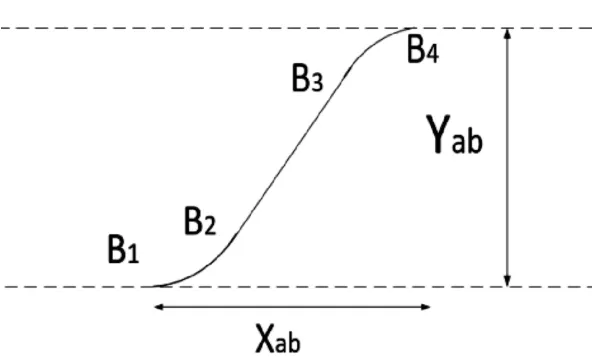
图2 圆弧变道模型

2.3 梯形加速度变道模型

坐标系纵轴是横向加速度，横向加速度的变换满足线性变换，切是关于对称的大小相等、方向正好相反的两个梯形，且加速度存在最大值，但是加速度变道模型相比较复杂，在实际车道变换的时候容易造成变换不灵活。

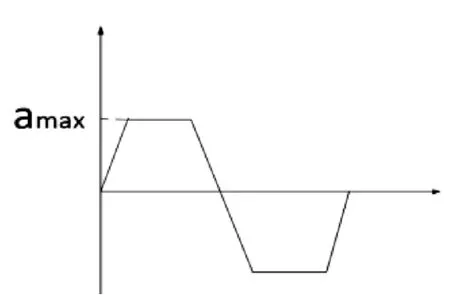
图3 梯形加速度变道模型

2.4 五次多项式曲线

五次多项式函数满足的一般表达式：

式中，y（t）是时间关于横向位移的函数关系，x（t）是时间关于纵向位移的函数关系，目前广泛应用于换道轨迹规划的就是五次多项式[2]，由于其一阶导、二阶导都具有连续性，换道过程中能满足车辆对平稳性、效率性、舒适性等的要求[3]，后面以五次多项式的最优轨迹的求解上也便于计算，对换道轨迹规划具有重要的作用和意义。

2.5 贝塞尔曲线

式中：Pi是表示控制点，Bi,n（t）是伯恩斯坦基函数；贝塞尔曲线简单易用，在初始点处与特征多变行相切，具有缩减性等良好的性质，且满足一阶导、二阶段连续，但是在实际的换道轨迹规划中，控制点的选取相对而言比较困难，主要用于解决整体形状的控制问题，在换道轨迹规划也有一定的应用。

曲线拟合法除了等速偏移模型、圆弧变道曲线模型、梯形加速度变道模型、五次多项式和贝塞尔曲线，还有样条曲线、等速偏移模型与正弦函数模型等，曲线拟合法与人工势场法比较起来，通过给定了起始点和终点，通过曲线拟合，能生成满足换道舒适性、安全性、效率等，还能满足动力性约束和其他约束的轨迹，在智能汽车换道轨迹规划上面具有十分重要的作用。

3 搜索算法

搜索算法在轨迹规划中，也是常用的方法之一。在搜索算法中，快速搜索随机树是应用的最广泛的，RRT 是一种多维空间中有效率的规划方法，它以一个初始点作为根节点，通过随机采样增加子节点的方式，生成一个随机扩展树，当随机树中的叶子节点包含了目标点或进入目标区域，便可以在随机树中找到一条由初始点到目标点的路径。

但是通过这种方法生成的曲线会存在曲线突变的现象，是的曲线不够平滑，在实际的换道的轨迹规划中也不易实现。

4 总结

随着自动驾驶技术的不断发展，换道轨迹规划已经具有越来越成熟的方法，目前人们在换道轨迹规划上面，应用最广泛的是拟合曲线法中的五次多项式曲线去拟合换道轨迹，既能生成具有舒适性、效率、安全等优点的曲线，也能满足实际中车辆的动力学约束和其他约束的要求，在换道轨迹规划中具有十分重要的作用。