形状可调3次三角域Bézier曲面及其几何迭代
徐梦豪,严兰兰
(东华理工大学理学院,330013,南昌)
0 引言
Bernstein多项式具有很多独特的性质,正因为如此,以Bernstein多项式作为基函数的Bézier方法拥有许多良好的特性。这使得Bézier方法自产生开始,便受到了来自工业界和计算机辅助几何设计(CAGD)学术界的广泛青睐[1]。虽然优点众多,但任何造型方法都不可能十全十美。Bézier方法的不足主要体现在2个方面:首先,Bézier曲线曲面的形状由其控制顶点唯一确定,当需要对形状进行修改的时候,唯一的办法是调整控制顶点,重新计算曲线曲面上的点。这种方式不仅操作起来不方便,而且如果控制顶点是来自实物的精确测量点,那么修改控制顶点本身就是勉为其难。另外,虽然Bézier方法可以表示灵活多变的自由曲线曲面,但却无法精确表示部分常见的初等解析曲面,只能采用近似表达,带来的后果是会引起设计误差,使原本简单的问题变得异常复杂。
对于Bézier方法的上述2个不足,有理Bézier方法在一定程度上能够克服,但有理方法自身又有其不足。例如:微分、积分等运算比较复杂,不恰当的权因子可能会破坏参数化。为了扬长避短,在保留Bézier方法优点的同时,避开上述这些不足,构造新的造型方法成为CAGD中的热点研究主题之一。
Bézier方法包括Bézier曲线、四边域张量积Bézier曲面、三角域Bernstein-Bézier曲面,这三者都面临着上述对于固定控制顶点形状无法调整的不便,以及无法给出除抛物线(面)以外的二次曲线(面)的精确表达的不足。
相对于曲面而言,曲线的结构比较简单,因此讨论更方便。已有众多文献专门围绕Bézier曲线的不足加以改进。改进的途径主要有2种:1)通过构造含参数的基函数,来实现不改变控制顶点也能修改曲线形状的目标[2-3];2)通过在非多项式空间中构造合适的基函数,来实现无需有理形式也能精确表示二次曲线的目标[4-5]。四边域上的Bézier曲面是采用张量积方法构造的,因此其采用的是与Bézier曲线完全一致的单变量Bernstein多项式作为基函数。这样一来,只要实现了对Bézier曲线的改进,也就同时实现了对四边域张量积Bézier曲面的改进。但由于三角域Bézier曲面并非张量积形式,其采用的是双变量Bernstein多项式作为基函数,所以要实现对三角域Bézier曲面的改进,需要独立地构造基函数。现有文献中,对Bézier曲线做改进研究的较多,对三角域Bézier曲面做改进研究的相对较少。
梳理国内外围绕三角域Bézier曲面的不足进行改进研究的文献, 根据其采用的基函数所在的空间将它们分为两大类。
第1类:依然在代数多项式空间中构造基函数,但基函数中融入了参数。例如文献[6-7]构造了3次双变量多项式基函数,定义了分别含3个、6个形状参数,且取特殊参数时都可以退化为2次三角域Bézier曲面的新曲面;文献[8-9]分别构造了3次、4次双变量多项式基函数,定义了分别含3个、1个形状参数,且取特殊参数时都可以退化为3次三角域Bézier曲面的新曲面;文献[10-11]都构造了n次双变量多项式基函数,定义了分别含1个、多个形状参数,且取特殊参数时都可以退化为n次三角域Bézier曲面的新曲面;文献[12]构造了n+1次双变量多项式基函数,定义了含多个形状参数,且取特殊参数时可以退化为n次三角域Bézier曲面的新曲面;采用递推的方式,在初始3次双变量多项式基函数的基础上,文献[13]构造了n+1次基函数,在初始4次双变量多项式基函数的基础上,文献[14-15]都构造了n+2次基函数,文献[13-15]中的曲面都含1个形状参数,且取特殊参数时都可以退化为n次三角域Bézier曲面。
第2类:在非代数多项式空间中构造基函数。例如在三角多项式空间中,文献[16]和[17]分别对2次、3次三角域Bézier曲面做出了改进,文献[18-19]在对3次三角域Bézier曲面做出改进的同时还引入了3个形状参数,文献[16-19]中曲面的边界曲线可以是圆弧、椭圆弧;在指数函数和多项式函数的混合空间中,文献[20]构造了含3个形状参数,且取特殊参数时可以退化为3次三角域Bézier曲面的新曲面;同样是在三角多项式空间,文献[21]构造了一种结构较为特殊的三角域Bézier曲面,其每张曲面片由19个控制顶点定义,该曲面可以精确表示球面。
得益于所融入的形状参数,由文献[6-15]定义的曲面不仅继承了传统Bernstein-Bézier曲面的基本性质,而且都可以实现不改变控制顶点,仅通过调整形状参数来修改形状的目标,因此这些新曲面使用起来更加灵活、方便。由于文献[16-17,21]构造的曲面都未引入形状参数,因此它们都并不具备形状可调性。虽然文献[16-19,21]构造的曲面定义于三角多项式空间,具备表示部分2次曲面的潜能,但只有文献[17]讨论了球面的表示。
考虑到代数多项式函数在所有函数类型中计算最简单,且基于代数多项式函数的曲线曲面易于向CAGD中的传统造型曲线曲面转化,因此在构造新曲线曲面时,若能保持调配函数类型为代数多项式,且新方法在保留传统曲线曲面基本性质的同时,还能获取一些新的性质,则不失为好的方法。
在工程实际中,低次曲线曲面的使用频率较高,因此本文选择3次三角域Bézier曲面作为改进对象。通过在控制顶点中融入参数,定义了含3个形状参数的新曲面,取特殊参数时可以退化为3次三角域Bézier曲面。对曲面的G1光滑拼接条件以及几何迭代算法进行了讨论,并对迭代算法的敛散性进行了分析。
1 曲面及其性质
1.1 曲面构造过程
给定三角域D={(u,v,w)|u,v,w≥0,u+v+w=1},以及呈三角阵列的控制顶点Vijk(i+j+k=3)∈3,可定义一张三角域上的3次Bézier曲面

曲面r(u,v,w)具备凸包性、角点插值性以及轮换对称性;由边界控制顶点确定的Bézier曲线构成了曲面的边界曲线;由角点和与之相邻的2个控制顶点张成的平面为曲面在角点处的切平面。
注意到在控制顶点Vijk(i+j+k=3)给定的情况下,曲面r(u,v,w)的形状唯一确定。下面分析如何在顶点Vijk中融入形状参数,从而定义具有形状可调性的三角域曲面r*(u,v,w),同时保持r*(u,v,w)与r(u,v,w)的角点一致,并且角点切平面相同。
为此,定义曲面r*(u,v,w)如下:
r*(u,v,w)=B300V300+B030V030+B003V003+
B111V111+B210[αV210+(1-α)V300]+B120[αV120+(1-α)V030]+B021[βV021+(1-β)V030]+B012[βV012+(1-β)V003]+B102[γV102+(1-γ)V003]+B201[γV201+(1-γ)V300]
(1)
其中u,v,w∈D,参数α,β,γ∈(0,1]。
将r*(u,v,w)记作
(2)
也就是将r*(u,v,w)当作常规的3次三角域Bézier曲面来看待,其控制顶点如下:
(3)

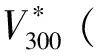
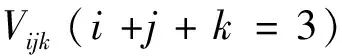
1.2 调配函数及其性质
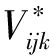
(4)
(5)
其中参数α,β,γ∈(0,1]。
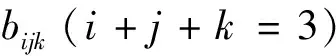
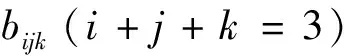
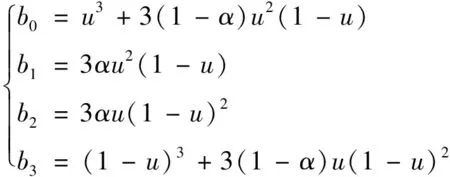
(6)
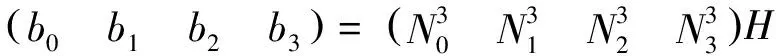
(7)
其中转换矩阵为
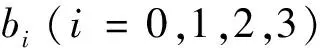
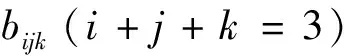
1)退化性。取α=β=γ=1,含参数的调配函数退化成双变量3次Bernstein基函数。
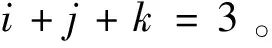
4)轮换对称性。当α=β=γ时,有
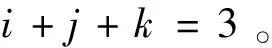
6)角点导数。对i+j+k=3,有
7)线性无关性。若参数α,β,γ∈(0,1],则含参数的调配函数之间是线性无关的。
证明:假设
(8)
其中xijk∈。将式(5)代入式(8)并整理,得到
x300B300+x030B030+x003B003+x111B111+[αx210+(1-α)x300]B210+[αx120+(1-α)x030]B120+
[βx021+(1-β)x030]B021+[βx012+(1-β)x003]B012+[γx102+(1-γ)x003]B102+[γx201+(1-γ)x300]B201=0。
由于普通的双变量3次Bernstein基函数之间是线性无关的,因此有
注意到α,β,γ≠0,故方程组的解为xijk=0,i+j+k=3,这表明bijk(i+j+k=3)线性无关。
1.3 曲面性质
根据调配函数的性质,并结合曲面r*(u,v,w)的表达式,不难推出形状可调三角域曲面的下列性质。
1)凸包性。曲面r*(u,v,w)完全落在其控制网格形成的凸包内部。
2)几何不变性与仿射不变性。曲面r*(u,v,w)的形状直接取决于其控制顶点以及参数α、β和γ的取值,与坐标系的选择无关;对曲面进行仿射变换,其结果与对控制网格进行同样的变换后所确定的曲面完全一致。
3)角点插值性。控制网格的3个角点都落在曲面r*(u,v,w)上,具体地,有r*(1,0,0)=V300,r*(0,1,0)=V030,r*(0,0,1)=V003。
4)角点切平面。在角点(1,0,0)处,曲面的切平面由点V300、V210和V201张成;在角点(0,1,0)处的切平面由点V030、V120和V021张成;在角点(0,0,1)处的切平面由点V003、V012和V102张成。
5)边界曲线。曲面上w=0的边界曲线由边界控制顶点Vij0(i+j=3)与式(6)所示函数组定义的曲线;曲面上u=0的边界曲线由控制顶点V0jk(j+k=3)与式(6)所示函数组(将参数α改为β)定义的曲线;曲面上v=0的边界曲线由控制顶点Vi0k(i+k=3)与式(6)所示函数组(将参数α改为γ)定义的曲线。由于函数组bi(i=0,1,2,3)具有全正性,因此边界曲线具备保形性。
6)形状可调性。在控制顶点Vijk(i+j+k=3)给定的情况下,可通过改变参数α、β和γ的值来调整曲面形状。
1.4 参数对曲面形状的影响
首先,由曲面边界曲线性质可知,当α保持不变时,对应w=0的边界曲线固定不变(比较图1(a)~图1(d));当β不变时,对应u=0的边界曲线不变(比较图1(b)、图1(c)、图1(e)和图1(f)或图1(d)和图1(g));当γ不变时,对应v=0的边界曲线不变(比较图1(b)、图1(e)和图1(f)或图1(d)和图1(g))。
另外,由表达式(4)可知,曲面r*(u,v,w)为控制顶点Vijk(i+j+k=3)的加权线性组合,点Vijk处的权重为bijk。而由式(5)可知,函数b300关于α和γ单调递减,b210和b120关于α单调递增;函数b030关于α和β单调递减,b021和b012关于β单调递增;函数b003关于β和γ单调递减,b102和b201关于γ单调递增。因此当α增加时,点V210和V120的权重增加,点V300和V030的权重减小,曲面对应w=0的边界曲线随α的增加而逼近以V210和V120为端点的线段,随着这条边界曲线的变化,整张曲面也会发生相应的改变(对比图1(b)、图1(e)和图1(f))。增加β(比较图1(c)和图1(d))或增加γ时的效果类似。当α、β和γ中有2个同时增加时,就有对应的2条边界曲线发生明显改变,例如当α固定,β和γ同时增加时的效果可以比较图1(a)、图1(b)和图1(d)。当α、β和γ三者同时增加时,3条边界曲线均发生明显改变,整张曲面对控制网格的逼近程度会不断增加,可以通过比较图1(a)、图1(e)和图1(g)来观察效果。
在固定控制顶点的前提下,图1展示了通过调整参数生成的形状各不相同的三角域曲面。
(a)参数 参数
与现有的形状可调三角域曲面相比,这里定义的形状可调三角域曲面具有如下优点:1)在赋予曲面形状调整灵活度的同时,并没有增加调配函数的多项式次数;2)边界曲线具有对边界控制顶点的保形性;3)曲面中含有的形状调整参数数量达到了同等条件下的最大值,因此具有最佳的形状调整灵活度。
2 曲面拼接
虽然含参数的调配函数依然为代数多项式,计算相对简单,但由于引入了参数,所以其表达比Bernstein基函数要复杂一些。这样一来,直接分析形状可调三角域曲面的拼接问题,虽然在理论上是可行的,但是实际操作起来具有一定的困难。为了降低分析的难度,依据3次三角域Bézier曲面的拼接理论,以及形状可调三角域曲面与3次三角域Bézier曲面之间的关系,来分析形状可调三角域曲面为实现光滑拼接应满足的条件。
2.1 3次三角域Bézier曲面的拼接
给出如下2张3次三角域Bézier曲面:
其中u,v,w∈D。当
(9)
时,r1(0,v,w)=r2(0,v,w),两曲面具有公共的对应u=0的边界曲线。为使曲面沿公共边界G1连续,须满足[19-21]
(10)
其中ξ和η为任意因子。条件(10)可转化为
(11)
根据式(9)、式(11),可以推出3次三角域Bézier曲面的G1光滑拼接条件为
(12)
2.2 形状可调三角域曲面的拼接
给出如下2张形状可调三角域Bézier曲面:

(13)
其中u,v,w∈D,bijk(u,v,w;α1,β1,γ1)表示参数取α1、β1和γ1的调配函数,bijk(u,v,w;α2,β2,γ2)则取参数α2、β2和γ2。
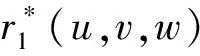
(14)
由式(9)可知,当
(15)
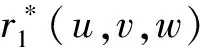
(16)
进一步地,由式(11)可知,若
(17)
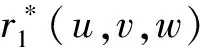
(18)
将式(16)代入式(18)并整理可得
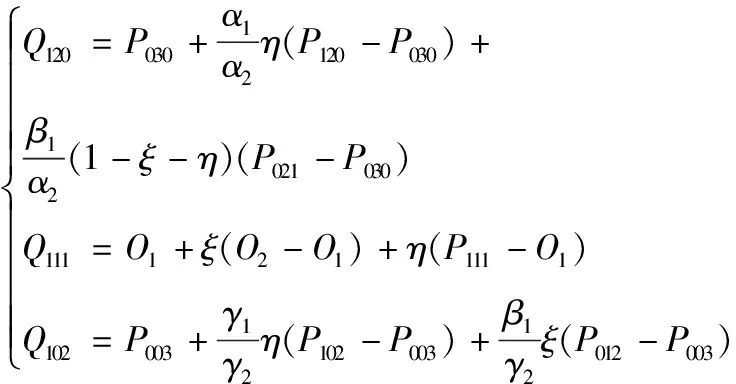
(19)
其中O1=β1P012+(1-β1)P003,O2=β1P021+(1-β1)P030。
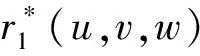
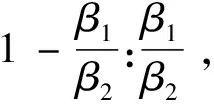
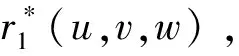
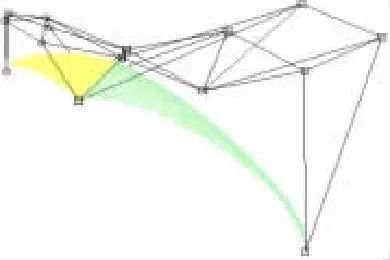
(a)参数(视角1)
3 曲面的几何迭代算法
几何迭代法[22]具有明确的几何意义。这种方法始于一条曲线或者一张曲面,通过不断地迭代调整曲线或曲面的控制顶点,让最终生成的曲线或曲面要么插值、要么逼近最初所给的控制点列。
3.1 算法描述
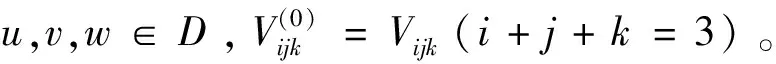
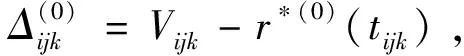
构造第1次迭代所生成的曲面
假设第n次迭代后得到的曲面为
为进行第n+1次迭代,首先计算差向量
(20)

构造第n+1次的迭代曲面
3.2 收敛性分析
按照3.1节中给出的迭代过程,不断地进行下去,将会生成一个曲面序列
为了分析迭代过程的收敛性,依据字典排序方法[23],将含参数的调配函数按以下顺序排列
b={b300,b210,b201,b120,b111,b102,b030,b021,b012,b003}
(21)
同步地,与控制顶点对应的参数也依据字典排序方法进行排列,并记
t={t300,t210,t201,t120,t111,t102,t030,t021,t012,t003}
(22)
由式(20)可得
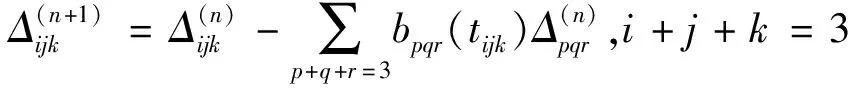
(23)
记
则式(23)可用矩阵表示成Δ(n+1)=(I-C)Δ(n),其中I为10阶单位矩阵,C为调配函数(21)关于参数序列(22)的配置矩阵,即
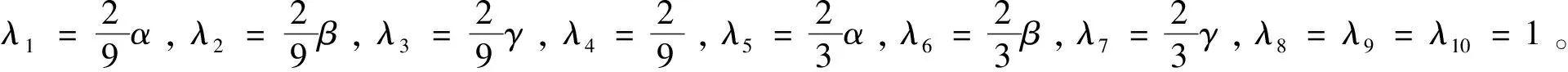
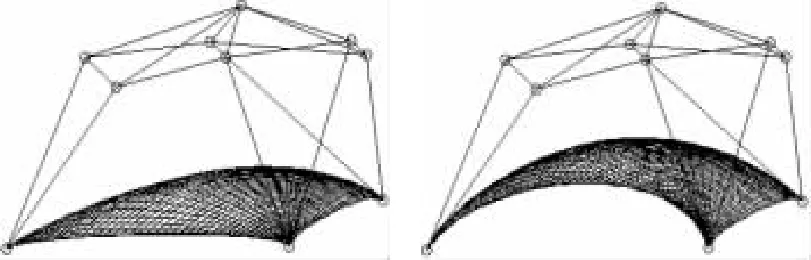
图3所示为:在球面上挑选10个点作为控制顶点,选择相异的2组参数,执行不同的迭代次数,得到的曲面结果。
将图3中第1列和第2列的4张曲面分别进行比较,不难看出,当迭代次数逐渐增加时,曲面逐渐变化到插值于给定点列的曲面。分别比较图3中每一排的2张曲面,不难观察出,参数取值越大,曲面与极限结果的插值曲面愈加接近。

(a)迭代0次:(左); α=β=γ=1(右) (b)迭代3次:(左); α=β=γ=1(右)
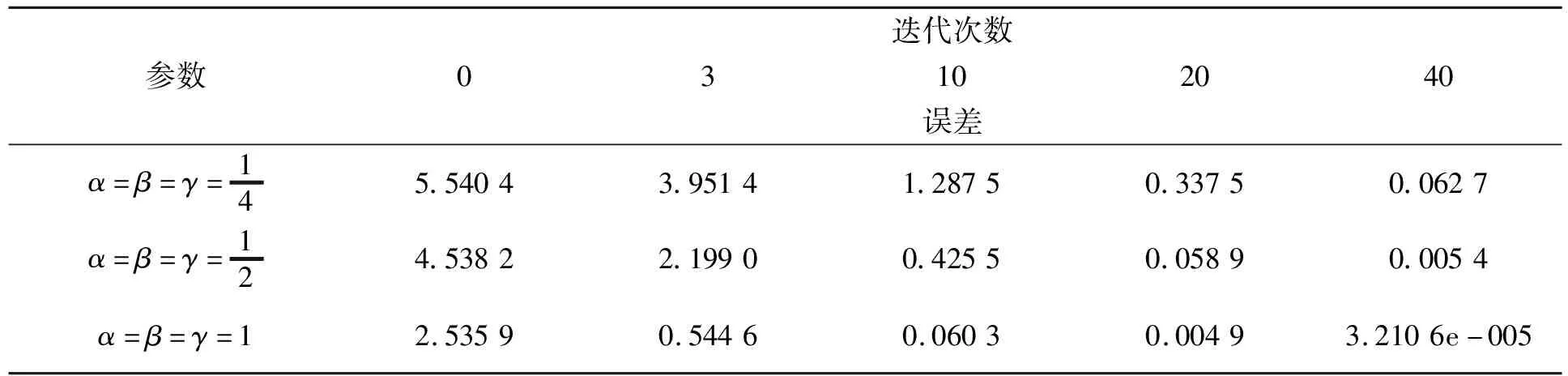
表1 迭代误差
4 结束语
以3次三角域Bézier曲面作为研究对象,本文欲从形状表示的灵活性这个角度对其进行扩展,在既没有改变基函数的类型(与文献[18-20]相比),又没有增加基函数的次数(与[6,7,9,12-15]相比)的前提下,赋予了曲面形状可调性,这些特点与文献[8,10-11]相同。本文给出的曲面含3个形状参数,比只含1个形状参数的文献[10]能构造出更加丰富的形状。文献[8]中的曲面和文献[11]中n=3时的曲面一致,虽然也含3个形状参数,但本文中的3个参数分别控制曲面的3条边界,参数的变化引起边界的变化进而带动曲面形状的改变,文献[8,11]中的3个参数则没有这种直观的调控作用。为了构造形状可调的三角域曲面,现有文献采用的方法基本相同,即先构造带有参数的调配函数,然后与控制顶点做线性组合,参数值改变时,参与计算的调配函数随之改变,从而引起曲面形状的变化。本文采用全新的思路,在控制顶点而非调配函数中融入参数,然后与常规的双变量Bernstein基函数做线性组合,以构造曲面。随着参数取值的改变,参与计算的曲面控制顶点随之变化,进而带动曲面形状的变化。这种方法从纯几何而非代数的角度出发,给出了可调曲面之所以形状可调的直观解释,即控制顶点的改变引起曲面形状的改变。
在讨论形状可调三角域曲面的光滑拼接条件时,为了降低分析的难度,先对常规3次三角域Bézier曲面的拼接条件进行讨论,再根据新曲面与3次三角域Bézier曲面之间的关系,得到形状可调三角域曲面的G1光滑拼接条件,条件的几何意义明确,这有利于手工确定与已有曲面光滑拼接的曲面控制顶点。
为了构造视觉上插值于控制顶点的曲面,对文中构造的形状可调三角域曲面的几何迭代算法做出了讨论,对迭代算法的收敛性、收敛速度以及拟合误差进行了分析,这些理论分析结果为曲面的应用打下了基础。

