数学形态学与布料模拟滤波算法适用性分析

王 凯，鲁铁定*，鲁春阳，刘 盈

(1.东华理工大学测绘工程学院，330013，南昌；2.河南城建学院测绘与城市空间信息学院，467036，河南，平顶山；3.井冈山大学电子与信息工程学院，343009，江西，吉安)

0 引言

机载激光探测和测距(LiDAR)作为一种高效、快速的大面积采集三维(3D)点云的遥感技术，已经在各个领域得到了广泛的应用，例如生成数字地形模型(DTM)[1]、森林生态系统调查[2]和三维建筑建模[3]。大多数点云数据应用中，区分为地面点和非地面点是一个必不可少的步骤，该过程也称为点云滤波。在过去的几十年中，众多学者根据不同的理论基础，提出了许多自动过滤地面点的点云滤波算法，这些算法主要可分为6类[4]。

基于数学形态学的点云滤波算法具有原理简单、实现效率高的特点，被众多学者研究，并进行相关改进。形态学滤波(Morphological filters)首先应用于数字图像处理，其能够去除图像中的细小部分，从而使图像更加平滑。Lindenberger[4]等首先将数学形态学方法引入到机载LiDAR点云滤波中。Zhang[5]等提出了一种经典的渐进形态学滤波方法。在该方法中，滤波窗口按一定的规则从小到大，不同的滤波窗口对应不同的高程阈值。此后，许多学者大都基于此方法进行形态学滤波算法改进。改进主要从以下3个方面入手[6]：1)进行格网误差的改进；2)对地形坡度、最大滤波窗口、高差阈值等参数设置的改进；3)地形坡度常量假设的改进。尽管已经产生了许多不同的改进算法，但是基于数学形态学的滤波算法对滤波窗口大小的选取敏感，以及很容易对陡峭地形中的点进行错误分类，如何提高基于形态学的滤波算法在地形起伏较大的区域中的鲁棒性仍是众多学者研究的重点与难点。

Zhang[7]等2016年提出的布料模拟滤波算法(CSF)，因其用户定义的参数少且易于设置，开始受到广泛关注。张凡[8]等将布料模拟算法在LiDAR点云中进行生成DEM实验，结果表明该算法生成的DEM能够很好地表现连续起伏区域的地形和细节特征，与实际地表地形能够很好地拟合。李雅盟[9]等提出一种顾及地形特征的布料模拟滤波改进方法，采用基于坡度的动态格网分割方法，对粗差剔除后的点云建立格网索引；然后利用每个格网的邻域格网中的最低点建立曲面方程来拟合高程值，最后计算真实高程与拟合高程差值从而实现高程归一化；最后使用布料模拟算法模拟布料下降过程得到地形布料的最终形态，进而通过限定阈值实现地面点提取。结果表明，该改进算法在保证大范围复杂场景区域滤波正确率的基础上，对不同地形具有较强的自适应性，且提高了滤波计算效率。Cai[10]等提出了一种将CSF和渐进不规则三角网加密(PTDF)相结合的滤波算法。在所提出的算法中，利用CS得到了一种高质量的初始临时数字地形模型(DTM)，并根据统计分析，从初始临时DTM中估计PTD的参数阈值。最后，利用具有自适应参数阈值的PTD对初始临时DTM进行了细化。这些细化实现了滤波精度的提高以及相关参数的优化。该算法的滤波精度优于直接使用PTDF算法。此外，与公开的改进PTDF算法相比，该算法不仅精度高，且更实用。针对布料模拟的相关特点，在点云分类方面，佟国峰[11]等针对室外大场景提出了一种基于聚类分割的点云分类算法，该方法通过滤除法向量差大的点改善地面滤波效果，为后面的点云分割提供了更好的非地面点数据。在点云精简算法方面，李绕波[12]等提出一种基于布料模拟滤波、方法库和曲率分级等综合算法的点云精简优化方法。由于布料模拟滤波算法(CSF)提出时间较晚，对布料模拟的其他相关应用，众多学者还在不断开发研究中。

本文通过对提出时间早、做过大量相关改进的经典的数学形态学滤波与最近提出的相关应用和改进都做的较少的布料模拟滤波算法进行滤波实验并进行精度评定。比较、分析和总结2种滤波算法的优缺点，对其适应性进行分析，希望能够对以后相关算法的研究有参考借鉴意义。

1 点云滤波原理

1.1 数学形态学滤波

数学形态学滤波算法原理：点云在进行形态学运算后非地面点的高程会发生很大的变化。将高度差大于阈值的点分类为非地面点并进行滤除。滤波窗口的大小对滤波结果的影响很大。

膨胀、腐蚀，闭运算和开运算是构成数学形态学运算的4个公式。f(x,y)为输入图像，b(x,y)为“结构元素”，定义如下。

1.1.1 膨胀 结构元素b对f进行灰度膨胀记为(f⊕b)，如式(1)：

(f⊕b)(s,t)=max{f(s-t,t-y)+b(x,y)|(s-x),(t-y)∈Df;(x,y)∈Db}

(1)

其中Df和Db分别是f和b的定义域。膨胀运算是在由结构元素确定的领域中，选取(f⊕b)的最大值。

1.1.2 腐蚀 结构元素b对f进行灰度腐蚀记为(fΘb)，如式(2)：

(fΘb)(s,t)=min{f(s+t,t+y)+b(x,y)|(s+x),(t+y)∈Df;(x,y)∈Db}

(2)

其中Df和Db分别是f和b的定义域。腐蚀是在由结构元素确定的领域中选取(fΘb)的最小值。

1.1.3 闭运算和开运算 由膨胀和腐蚀进行组合。

闭运算，用b闭运算f，记为f·b，定义如式(3)：

f·b=(f。b)⊕b

(3)

将结构元素内的所有数据填充为区域最大值，然后再填充为该区域最小值。

开运算，用b开运算f，记为f。b，定义如式(4)：

f。b=(f。b)⊕b

(4)

将结构元素内的所有数据填充为区域最小值，然后再填充为该区域最大值。

在渐进形态学滤波时，滤波结果的好坏对滤波窗口的大小选取十分敏感。对于滤波窗口的增长方式，本文选择方法是通过线性方式增加窗口大小，如式(5)：

wk=2kb+1

(5)

其中k=0,1,2,3,…,m；b是初始滤波窗口，最大滤波窗为2mb+1；采用2kb+1作为窗口大小可保证滤波窗口绕中心点对称，简化了开运算。线性增加窗口大小的优点是可以有效地保留渐进变化的地形特征。但是，对于具有大型非地面物体的区域，则需消耗大量的计算时间。

高程阈值可基于研究区域的地形坡度决定，对于最大高程差与地形dhmax(t)，k，窗口大小wk和地形坡度s的关系如公式(6)，得出坡度常数。

(6)

因此，高程阈值dhT,k可由公式(7)得：

(7)

其中：dh0是原始高程阈值；s是坡度；c是单元格网大小；dhmax是最大高程阈值。

以指数方式增长的滤波窗口优点在于增长速度快、效率高，但缺点在于滤波精度与线性增长方式相比效果不是很好。因此，本文采取滤波窗口线性增长方式。窗口大小wk和高程阈值dhT,k上增长方式如式(6)、式(7)所示，使用C++语言与点云库PCL相结合，并将所得的点云数据在VS2013平台上进行数学形态学滤波实验。

1.2 布料模拟滤波

CSF算法原理：首先使用布料模拟(CS)估算初始地形，然后基于实际地形应在某个局部区域内接近水平面的假设，仅通过使用高程信息将未过滤点的地面点添加到初始地形。布料模拟滤波算法(CSF)，首先将LiDAR点云翻转倒置，即将点云坐标中的z变为-z，此后布料粒子因受重力影响而下降，通过分析布料节点与相对应的LiDAR点云之间的作用关系，从而确定布料粒子最终所处的位置，以此来确定布料最后所形成的形状，从而达到点云滤波的目的，布料模拟过程如图1所示[6]。

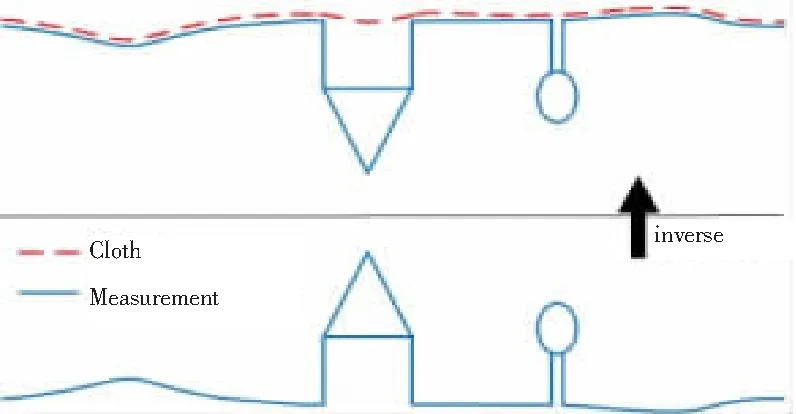
图1 布料模拟过程图

由于限制了布料粒子的移动方向，因此2个具有不同高度的粒子将试图移动到同一高度。若2个相关联的粒子都为可移动的，则沿相反方向将它们移动相同的位移。如果其中一个不可移动，则另一个将被移动。否则，若这2个粒子有同一的高度值，则不移动。因此，通过式(8)计算每个粒子的位移(矢量)：

(8)

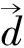
图2 刚性参数化

CSF的主要过程如下：先将布料粒子和LiDAR点云投影到同一水平面，其次在此2D平面中为每个布料粒子找到与其相临近的LiDAR点(称为对应点，CP)。定义交叉点高度值(IHV)以记录CP的高度值(投影前，该值表示粒子可以到达的最低位置)。每次迭代过程中，将该粒子的当前高度值(CHV)与IHV进行比较；若CHV≦ IHV，则粒子移回IHV的位置，并设为不可移动。

CSF主要由4个用户定义的参数组成：网格分辨率(GR)，表示相邻粒子之间的水平距离；时间步长(DT)，表示每次迭代过程中粒子受重力影响而产生的位移；刚性度(RI)，其控制布料的刚度；距离阈值(hcc)，该距离阈值根据与布料网格的距离决定将LiDAR点的最终分类为BE(地面点)和OBJ(地物点)。

CSF算法的实现过程如下。

1)使用第三方软件(如Cloudcompare)自动或手动去除躁。

2)使原始LiDAR点云倒置。

3)布料格网的生成，根据网格分辨率(GR)确定粒子数,布料的起始位置一般设置在最高点之上。

4)将所有LiDAR点云和网格粒子投影到一个水平面，并找到该平面中每个网格粒子的对应点(CP)，并记录IHV。

5)对每个布料粒子，若该粒子为可移动，计算其受重力影响产生的位移，并将该粒子的高度与IHV进行比较。若粒子的高度≦IHV，则将该粒子置于IHV的高度，并设为“不可移动”粒子。

6)计算每个布料粒子受内力影响产生的位移距离。

7)重复5)～6)至所有布料粒子的最大变化高度足够小或超设定的最大迭代次数时，则布料模拟停止。

8)计算布料粒子与其相对应点(CP)之间的距离。

9)区分地面点和地物点。若每个LiDAR点到模拟粒子的距离小于距离阈值(hcc)，分类为BE(地面点)，否则分类为OBJ(地物点)。

除了这些用户定义的参数外，根据CSF算法原理，当将原始LiDAR点云倒置时，地面上方的物体将出现在地面测量点以下。因此，根据实验样本地形特征的不同，在视觉上将实验样本分为不同的组别，以此依据来设定滤波参数。例如地形非常平坦且没有陡峭或有坡度的梯田，则将RI设置为相对较大的值(RI= 3)，且不需要坡度处理(ST=false)；如存在陡峭的斜坡(例如河岸、沟渠和梯田)，则需要中等软布(RI=2)且需要进行坡度处理(ST =true)；当处理非常陡峭的斜坡时，需要非常柔软的布料(RI=1)且需要进行坡度处理(ST=true)。

2 实验结果与分析

由于Zhang[5]等提出的渐进形态学滤波方法最为经典，较具有代表性。此后的相关数学形态学滤波方法的改进大都是基于这种经典算法的改进，本文选用Zhang[5]等提出的渐进形态学进行点云滤波实验，与Zhang[7]等2016年提出的布料模拟的滤波算法进行实验，最后分别对2种滤波算法进行精度评定并进行适应性分析。实验数据采用ISPRS(国际摄影测量和遥感学会)数据，对2种算法的性能进行了测试，该实验数据由Optech ALTM扫描仪收集，包括由不同地形环境组成的8个站点(命名为站点1～8)：4个城市站点和4个农村站点。从站点1～7中选择了15个具有不同地形特征和土地覆盖类型的参考样本，进行滤波精度评定。由于缺乏参考数据，因此站点8被排除在外。对于每个实验样本，参考数据是用先验知识和可用的航空图像手工识别生成的[13]，15组样本数据地形特征如表1所示。

表1 15组样本的地形特征

本文实验数据使用C++语言与点云库PCL相结合，并将所得的点云数据在VS2013、点云处理软件Cloudcompare进行数据处理。为尽量避免不同噪声点对滤波结果的影响，在进行滤波实验前，15组样本数据都通过手工进行了去噪处理。此外，为定量分析2种算法的滤波性能，根据ISPRS规定的Ⅰ类误差(将地面点错分为地物点的误差)、Ⅱ类误差(将地物点错分为地面点的误差)和总误差对实验结果进行定量精度评定分析。15组样本数据滤波实验结果Ⅰ类误差、Ⅱ类误差和总误差如表2所示。

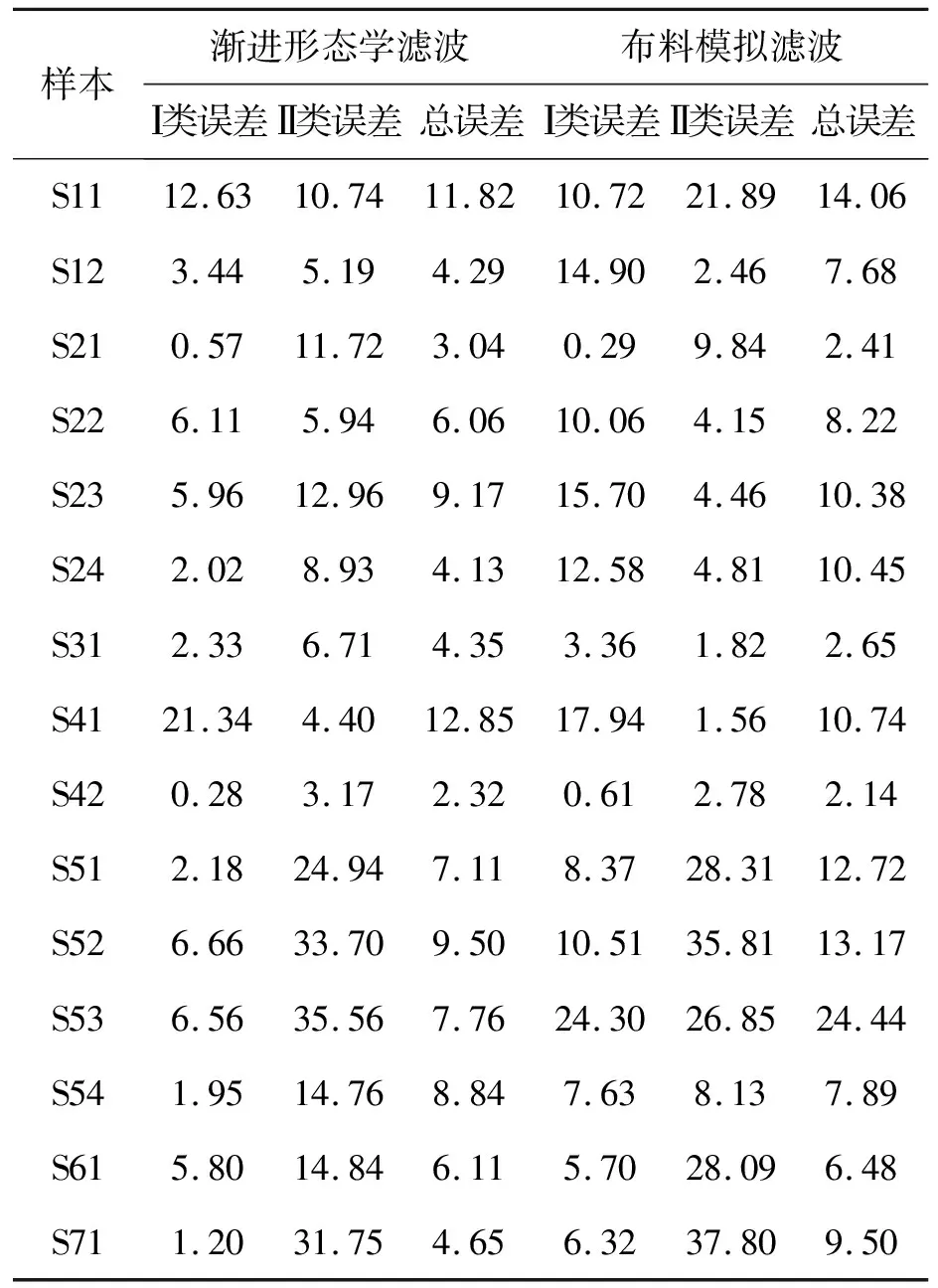
表2 2种算法滤波结果

从表2中可以看出，2种算法在地形平坦区域(S21、S31、S42、S51、S54)都取得了良好的滤波效果，Ⅰ类误差、Ⅱ类误差和总误差都处于较低水平，较具有代表性的有S21、S31，如图3、图4所示。

(a)S21 DSM (b)参考DEM

(a)S21 DSM (b)参考DEM

2种算法在城市等综合复杂地形区域(S11、S22、S23、S24、S41)滤波效果一般，由于数学形态学滤波算法需要一定的先验知识去预估最大建筑物尺寸，以设定最大滤波窗口大小，而CSF的局限性在于已将粒子运动的物理运动过程改为2个离散的步骤，当在城市等综合地形复杂区域处理超大型低矮建筑物时，布料粒子可能会粘在屋顶或低矮植被上，从而可能会将某些地物点错误地分类为地面点。所以2种算法在城市等综合复杂地形区域的滤波效果一般，优缺点各异。较具代表性的有S22、S24，如图5、图6所示。

(a)S22 DSM (b)参考DEM

(a)S24 DSM (b)参考DEM

在山区等陡峭地形区域(S52、S53、S61、S71)2种算法都取得了较差的滤波效果。此外，这4组样本数据都在乡村区域，地面点数量远大于非地面数量，地面上覆盖的大多数是植被及低矮灌木。在用数学形态学滤波算法时，选取相对小的滤波窗口就能获得相对好的滤波效果。而布料模拟滤波算法(CSF)，斜率是影响该滤波算法准确性的重要因素。斜坡上，模拟的布料会躺在斜坡上，但无法完美贴合粘附在地面上，即使进行后处理后，滤波精度的提升也相对有限。较具有代表性的有S52、S53，如图7、图8所示。

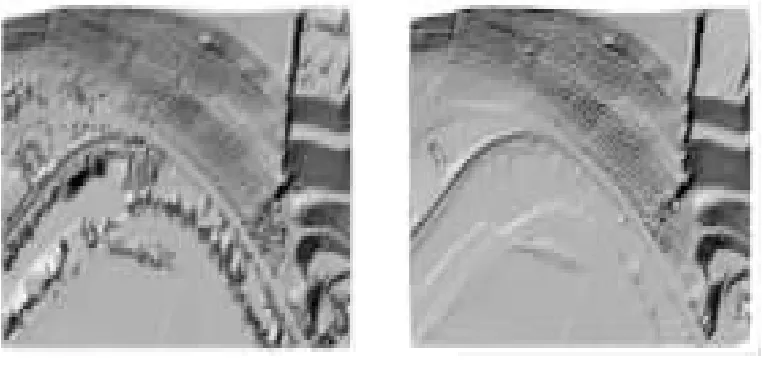
(a)S52 DSM (b)参考DEM

(a)S53 DSM (b)参考DEM

3 总结与展望

基于数学形态学的滤波算法原理简单、效率高，其缺点在于滤波窗口大小的选取，这需要对地形有一定的先验知识。布料模拟滤波算法(CSF)的优点在于用户定义的参数少且易于设置。但局限性在于将粒子运动的物理运动过程改为2个离散的步骤，当在城市等综合地形复杂区域处理超大型低矮建筑物时，布料粒子可能会粘在屋顶或低矮植被上，从而可能会将某些非地面点错误地分类为地面点。2种算法优缺点各异，在地形平坦区域都取得了良好的滤波效果，在城市等综合复杂地形区域取得了相对较好的滤波效果，但从便利性来看，由于形态学滤波需要一定的先验知识估算最大建筑物大小，从而确定滤波窗口大小的选取，布料模拟滤波在处理各类地形上更具便利性，设置参数少。2种算法在山区等陡峭地形区域取得了较差的滤波效果。这2种滤波算法和其他的滤波算法一样，在陡峭地形区域的滤波精度低，滤波效果差。如何有效提升地形陡峭区域的滤波精度，这也是机载LiDAR点云滤波算法一直研究的热点与难点。