MOSFET寄生参数对LLC谐振变换器性能影响研究*

沈 华，甄昊涵，童 涛，沈培刚，陈海敏，陈圣泽

(国网上海市电力公司电力科学研究院，上海 200090)

0 引言

随着电力电子技术的发展，对电子元器件自身造成的损耗要求越来越严格，人们期望通过技术的改变，大幅降低开关器件的功耗，达到节约能源，提升控制精度的目的。近年来，开关电源作为电力电子的一个重要应用方向，其频率日益高频化。然而，开关速度的提高，使某些在低频下能够忽略的寄生参数，如印制电路板的布线、器件封装形式导致的寄生电感以及开关器件的寄生电容，它们在高频的工作环境下，容易形成振荡[1]，给应用电路带来过高的电压和电流，增加了器件损坏的风险[2-3]。

为此，许多学者对于开关器件的寄生参数问题开展了大量研究工作。如文献[4-5]针对MOSFET开关器件的Miller电容的非线性问题进行了研究，得出了影响Miller电容非线性特性的一些因素和数学模型；文献[6]研究了MOSFET寄生参数(电感、电容、电阻)对 MOSFET开关器件开关性能的影响，对理论分析和实验结果进行了对比分析；文献[7]分别研究了栅极、漏源级回路中的寄生电感对开关器件的影响以及开关损耗的分析。

基于前人所做工作，本文以LLC谐振变换器作为研究对象，研究MOSFET寄生参数对电路性能的影响。

图1 LLC谐振变换器电路

常见LLC谐振变换器结构如图1所示，整个变换器由可控开关网络、谐振网络、变压器、整流网络以及低通滤波及负载构成；其中电路的谐振部分由谐振器件Lr、Cr以及变压器的等效漏感Lm共同构成，该电路由于存在两个参加谐振的电感元件而得名。

电路的谐振频率有两个：

其中fs为串联谐振频率，fmin为最小谐振频率。这种变换电路利用谐振网络谐振时，电压或者电流自然过零点的特性，对开关进行导通或者关断，从而形成软开关[8]，达到减小开关损耗的目的。这种电路通常采用变频控制，通过对开关动作频率的改变，实现改变谐振网络中各部分阻抗上的分压，最终达到调节输出电压的目的：当外界功率需求较低时，LLC谐振变换器的工作频率较高，超出谐振点fs，当功率需求较高时，控制回路降低开关频率。通常，LLC谐振变换器工作的理想的状态频率范围为：(1)高于 fs频率运行；(2)直接在 fs频率点运行；(3)介于fs和fmin频率点间运行，在这三种频率范围内运行的LLC谐振变换器，其变压器的输入阻抗呈现感性特性，此时输入的电流相位滞后于输入电压，变换电路才能保证MOS管实现零电压开关的功能。

通常，LLC谐振电路在一个周期内有多种工作模式的交替变换，即：

[t0-t1]阶段：开通延迟阶段。此阶段主要特点是在MOSFET的栅极和漏极间加脉冲电压，栅极将会产生电流 ICS，该电流将向 Cgd、Cgs充电。栅－源极间电压按式(3)所示的指数方式增长。

式中，UG为栅极电压；τg=(Rs+Rg)(Cgs+Cgd)为时间常数。在该阶段，由于MOSFET器件的工作状态没有改变，故此状态下的损耗为零。

[t1-t2]阶段：该阶段为电流上升阶段，由于寄生参数的存在，输出电压、电流都有一定变化，该阶段的漏极电流按式(4)规律变化，其中K为拟合系数，vt为阈值电压。

[t2-t3]阶段：Miller平台形成。在该阶段，漏极电感LS和电容Cgd形成了漏极至栅极间的反馈通路，导致漏极电流上升，栅极电压下降，形成Miller平台。当电感LD与电阻Rg相比很小时，即Rg很大时，漏极电流在未达到最大值前，漏源极电压将会有很大的跌落过程，此时栅-漏极间电压数学关系式见式(5)：

[t3-t4]开通末期，此时 Miller平台结束，vgs从 vgsp开始按指数的方式增长，在此阶段，由于寄生电容的非线性特性，该阶段电容值较大，导致开通延迟时间长。

此时MOSFET器件已经完全开通，漏极电流的上升速度与寄生电感参数决定。

[t4-t5]关断延迟阶段。该阶段器件的栅极电压发生变化，此时，Cgd、Cgs开始释放能量，栅-漏极间的电压以指数方式下降：

[t5-t6]Miller平台。当vgs=vgsp时，Crss开始将储存的能量进行释放，漏源间的电压按式(8)变化：

[t6-t7]电流下降阶段，vgs从 vgsp开始按指数的方式下降，该阶段Miller平台结束。

[t7-t8]此阶段振荡关断，漏源极间的电压出现明显的阻尼振荡，漏极电流开始下降，此时电路可等效为二阶电路。

至此，整个电路完成一次完整的开通到关断的过程。从变化的过程可以看出，电路的状态变化以及输出与MOSFET器件的寄生参数(电容、电感)都有关联，这些参数在变换过程中，呈现出非线性特性。因此，在电路参数的设计中，寄生参数的影响因素将不能忽略，尤其是对电压输出要求严格的场合。

1 MOSFET寄生参数建模

在图2所示的等效模型中，Cgd、Cgs以及 Cds分别表示MOSFET的栅极、漏极和源极之间的极间电容；LD和LS分别为漏极和源极之间的寄生电感；Rg为栅极寄生电阻。输入电容Ciss、输出电容Coss和反馈电容Crss之间的关系为：

输入电容Ciss、输出电容Coss和反馈电容Crss成为MOSFET的Miller电容，可用C表示。根据半导体器件的特性，Miller电容与漏-源极间的电压成对数关系，可由式(11)表示：

图2 MOSFET等效模型

其中 a、b为 Miller电容变化的对数拟合曲线系数；VDS为漏-源极电压。

对MOSFET的非线性物理基建模可以从器件的基本原理出发，根据器件的具体结构，尺寸大小以及物理方程计算来预测器件的工作性能。但是对于射频MOSFET应用而言，物理基模型存在只限于计算DC方程(计算S参数和大信号性能时间过长，对软件的要求也非常高)的缺点。Angelov模型是由Angelov等人提出的统一的FET模型，涵盖 MESFET、MOSFET、HEMT器件。模型从数学角度出发，引入了多项式和双曲正切tanh函数，将器件的直流DC I-V和交流ACC-V工作特性使用拟合公式来表述[9]。Angelov DC I-V 模型如式(12)～式(13)所示，Ipk是跨导达到最大时的漏源极电流，Vpk是跨导达到最大时的漏源极电压，α是电压饱和因子。1+γVDS被用来表征MOSFET器件的沟道长度随VDS调制变化的特性。

在本文的仿真中，首先基于Angelov模型，仿真电路中的开关MOSFET器件，并将仿真结果与厂方提供的技术参数进行对比，用以确认MOSFET寄生参数模型的有效性。

2 电路输出特性

在实际的电路设计中，可以利用基波分量法，将副边的等效负载折算到变压器的主边，可以得到交流的等效负载为：

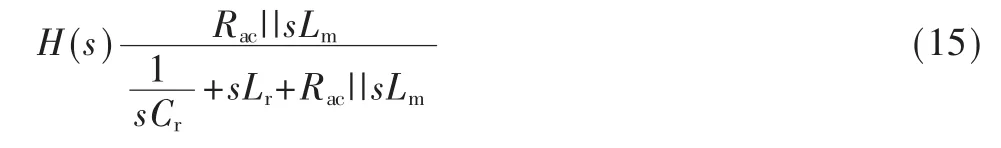
式中S表示为复频率，根据传递函数，系统对应的直流增益[10]为：

定义归一化电压增益M(f)为：

则对于任意频率下的电压增益，可表示为：

其中 fS为串联谐振频率，fn=f/fS为归一化频率，f为开关频率，n为变压器的变匝比。令，则系统的直流增益可以表示[11]为：

由上式可以看出，对直流增益有影响的因素有比例系数K、品质因素Q以及变压器的变匝比n。

3 模型仿真

为了研究寄生参数对电路输出特性的影响，本文首先将LLC电路中的开关器件建模为理想开关和考虑寄生参数的MOSFET，开关器件的模型如图3所示。图3中，真实开关模型是考虑了寄生参数的MOSFET器件，理想开关器件是将开关器件建模为理想二级管、开关以及等效电容构成，这些参数在仿真过程中都保持恒定值，其余参数设定为 Cr=100 nF；Lr=40 μH；Lm=170 μH；Rg=50 Ω。

图3 理想开关VS真实开关

为了验证MOSFET器件模型的正确性，利用第1节的寄生参数建模知识，将寄生参数的变化考虑进模型的搭建中，并以MOSFET元件厂家提供的出厂数据作为对比基准，不断修正拟合参数，最终得到图4、图 5所示的器件输出特性曲线，其中，图4表示了器件的输出特性，图5表示器件的转移特性。

图4 MOSFET输出特性

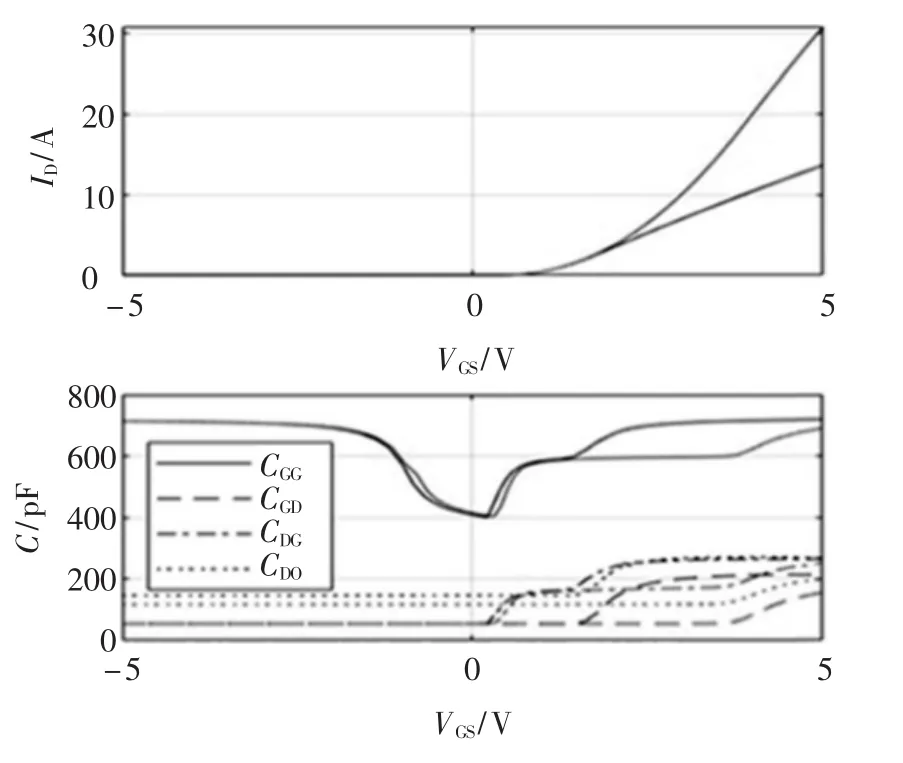
图5 MOSFET转移特性

图4是根据等效模型进行仿真得到的输出特性曲线，从图4可以看出，随着漏-源极间电压VDS的增加，寄生容量值减小。从图4还可以看出，输出特性分为截止、饱和与非饱和3个区域。当处于饱和区时，是漏极电流ID不随漏源电压VDS的增加而增加，基本保持不变。

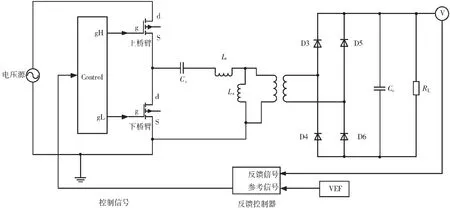
图6 仿真模型

图5反映了漏极电流ID和栅源间电压VGS的关系，称为 MOSFET的转移特性。由图可知，ID较大时，ID与VGS的关系近似线性，曲线的斜率为跨导 Gfs，此阶段，寄生电容随着VGS的增大而增大，但两者关系呈现出非线性特性，这与前面分析一致。

根据图1所示的LLC谐振电路，在MATLAB环境下搭建仿真模型如图6所示，图6中的上臂与下臂分别对应上开关MOSFET管和下开关MOSFET管，在仿真时，分别仿真开关特性为理想特性与实际特性时系统的输出，通过对输出的分析，比较寄生参数对电路的影响。仿真电路采用反馈控制机制，通过反馈，使系统的输出能够尽快达到输出的期望。

图7模拟了当MOSFET器件真实工作时，输出的变化曲线，从图7可以看出，整个电路在1.4 ms时，输出才能够达到期望值，该数值比期望输出时间(1 ms处)大约滞后0.4 ms，滞后特性反映了MOSFET开关的延迟导通性，其工作过程对应于[t0-t1]时间段的状态。同时，从图中可以看出，达到稳态输出时，开关的频率维持在75 kHz左右，即谐振频率，该频率与本电路设计的参数基本一致。

图7 电路输出曲线

从图8中的曲线对比可以看出，由于寄生参数的影响，输出达到稳态的电压的时间较理想时间有一定的延迟，但延迟时间大约为千分之一毫秒，这一时间对于普通的开关电路，其延迟可以忽略；此外，在稳态时输出电压较理想输出电压有很小的下降，大约2 V，当对电压精度要求较高时，需要在设计时考虑将该值。

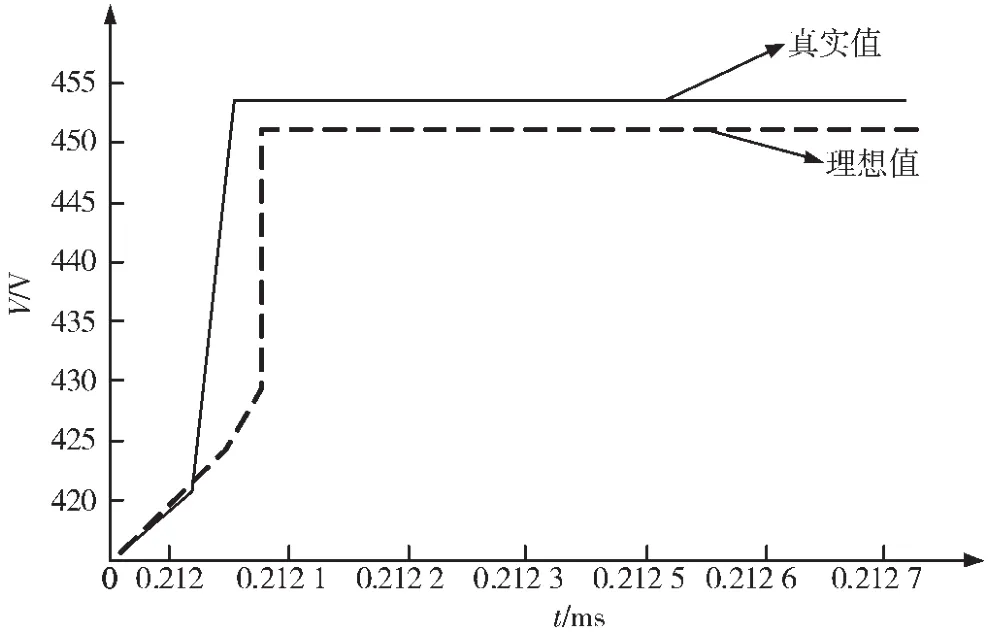
图8 电路输出对比

图9为理论谐振频率与实际谐振频率的对比，从图中可以看出，理论的谐振频率较实际的谐振频率要高，这是因为寄生电容的存在，导致等效电容变大，根据谐振频率计算公式可知，整体的频率将降低。通过对比可知，实际频率大概有70 kHz，较正常值减少了大概5 kHz，说明寄生电容的存在对系统的频率影响较大。在实际的电路设计中，在选择谐振电容、电感参数时，应将寄生参数的影响计入参数设计中，最大程度地消除寄生参数的影响。

图9 谐振频率对比

4 结论

本文分析了开关器件MOSFET的寄生参数对LLC谐振电路性能的影响。本文首先从寄生参数模型入手，对MOSFET的寄生参数建立了等效分析模型，并基于该分析模型，分析了寄生参数在MOSFET工作各阶段的影响，最后在MATLAB下建立了LLC谐振电路模型，实现了整个系统的仿真。仿真结果表明，本文利用的等效模型，可以准确反映MOSFET寄生参数对于LLC谐振变换器的影响。通过仿真结果对比发现，寄生参数的存在将对输出电压、谐振频率都有影响，尤其是谐振频率的影响较大，因此在高频电路设计时，需要对寄生参数重点关注，在电路参数选择时，需要计入寄生参数的影响。