铁路桥梁门式墩结构简化计算与快速设计

阮 良 奉

(中铁第五勘察设计院集团有限公司，北京 102600)

1 概述

近年来，随着我国高速铁路建设的快速发展，新建铁路与既有铁路、公路以及石油燃气管道的交叉变得越来越频繁。门式墩结构因其布置方式灵活、工期短、经济性好、可以有效地解决线路间小角度交叉的问题，在铁路工程中得到了广泛的应用[1]。

然而门式墩结构相比普通桥墩的设计要繁琐，荷载作用于横梁的位置是不确定的，横梁、墩柱、基础之间存在相互作用，往往需要反复试算确定最终的结构尺寸。目前随着有限元单元法的广泛使用，利用计算机进行结构分析已成为当前设计的主要计算手段。门式墩结构亦是如此，常使用Midas Civil建立空间有限元模型，用梁单元模拟横梁、墩柱和承台，利用等效刚度矩阵采用弹性支承约束模拟桩基础，然后对各荷载工况进行计算和组合以验算结构的刚度与强度[2]，建模过程并不复杂，但是单工点建模分析给批量设计带来困难。尤其是在设计准备阶段，通常根据以往设计经验拟定结构尺寸，试算后又频繁调整计算模型影响设计效率。因此门式墩结构的快速简算设计还是很有必要的。早在2003年刘彦文等[3]就针对轻轨框架墩结构采用力法进行纵向受力分析，但随着计算机的广泛应用，这种通过力学公式推导进行结构设计的方法不被设计者所好。其实通过力学公式推导可以很直观地得到结构自身的受力情况，有利于快速设计。

因此本文首先对铁路门式墩结构进行力学模型简化，再通过力法、位移法利用对称和反对称结构的特点[4]推导得出门式墩纵横桥向线刚度以及恒载、活载、温度、支座沉降、地震作用下的内力解析解，其中利用等效质量法将门式墩多质点体系用单质点体系代替[5]，减化地震力计算。最后结合工程实例对门式墩结构的墩顶线刚度、结构自振周期、横梁高度、预应力钢束面积、墩柱尺寸、桩基布置、桩长等进行简化计算与快速设计，并与Midas Civil计算结果进行对比。

2 简化计算模型

门式墩作为三维空间结构，横梁主要承受弯矩及剪力，墩柱主要承受弯矩及轴力，且横梁、墩柱及基础间均为固结，三者的内力、变形互相影响。因此要准确的计算出结构内力，就必须将横梁、墩柱与基础作为整体一起计算。

门式墩计算时可以简化分为平面内和平面外两个方向[6]。在平面内按框架结构简化，在平面外方向按悬臂结构简化，基础均按完全固结处理，如图1所示。其中ib=EIb/L为横梁线刚度；ic=EIc/H为墩柱线刚度；n=ib/ic为横梁与墩柱线刚度比值；a为线路中心到墩柱(荷载近侧)中心的距离a=mL≤b，m∈[0,0.5]。

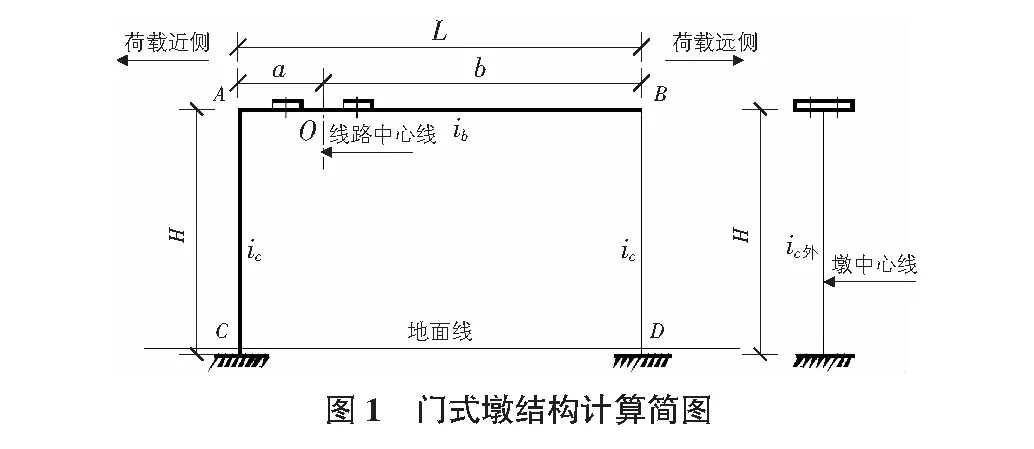
2.1 门式墩纵、横桥向刚度

铁路无缝线路设计规范中提出墩台最小线刚度的要求[7]，因此需要对门式墩纵横桥向线刚度进行简化计算。桥墩刚度k可以理解为墩顶作用单位水平力时，墩顶产生位移f的倒数，此位移由两部分组成，一是墩身的弹性水平变形f1;二是基础水平位移f2及基础转角引起的墩顶水平位移f3，因此可以得到式(1)。

(1)

其中,k1=1/f1为墩身刚度；k2=1/(f2+f3)为基础刚度。k1/k2可以根据线路地质情况大致确定，根据经济性要求通常k1/k2=3/2～7/3。则k=(0.3～0.4)k1。而k1则通过结构力学[4]推导得出：

1)顺桥向刚度：忽略横梁顺桥向的挠度变形，Ic外为墩柱平面外抗弯惯性矩。

(2)

2)横桥向刚度:Ic为墩柱平面内抗弯惯性矩。

(3)

2.2 门式墩结构内力简化计算

根据门式墩结构主要荷载类型[8]可以划分以下几种计算图式。并规定平面内横梁及墩柱弯矩以内侧受拉为正，外侧受拉为负；轴力以受压为正，受拉为负。

1)结构自重。

结构自重主要为材料自身重量，q为横梁自重线荷载，q′为墩柱自重线荷载，L为横梁跨度，H为横梁形心到墩柱底的高度，如图2所示。

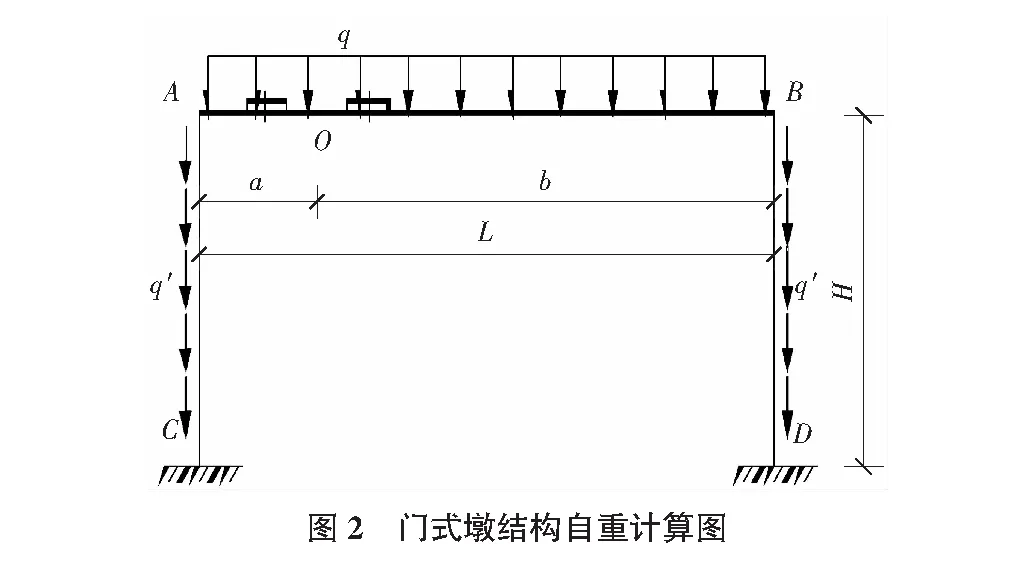
利用力法、位移法[4]可以计算得出各关键点位置的弯矩式、轴力式。墩柱、横梁剪力可以通过墩柱、横梁两端弯矩推算得出，下同。

(4)

(5)

2)横梁竖向荷载。

横梁竖向荷载主要为梁部恒载及列车活载引起的竖向反力。P为横梁竖向荷载，如图3所示。

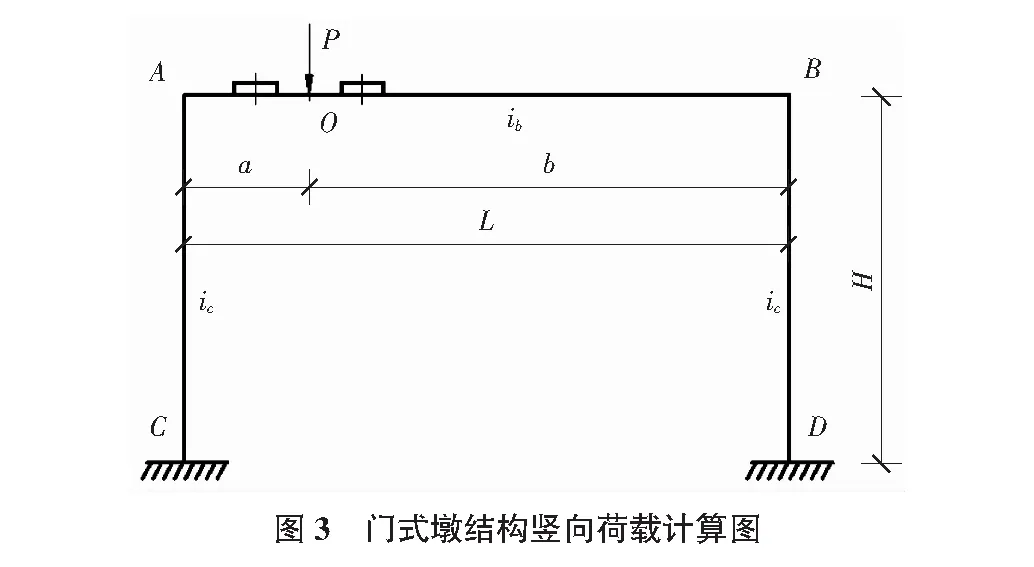
通过力法、位移法利用对称和反对称结构可以减少超静定结构约束变量，计算推导得出各关键点位置的弯矩式、轴力式。

从式(6)可以得出：当n→0,ib≪ic，则横梁刚度远小于墩柱刚度，相当于横梁两端固结。

当n→∞,ib≫ic,则横梁刚度远大于墩柱刚度，相当于横梁两端铰结则MA=MB=0。

(6)

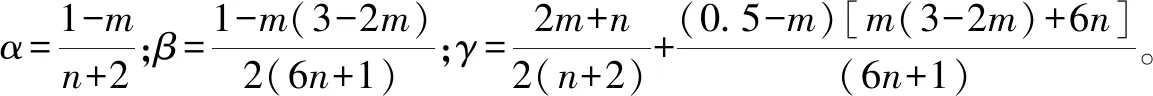
(7)

3)横梁水平荷载。

横梁水平荷载主要为列车离心力、摇摆力。F为横梁水平荷载，如图4所示。

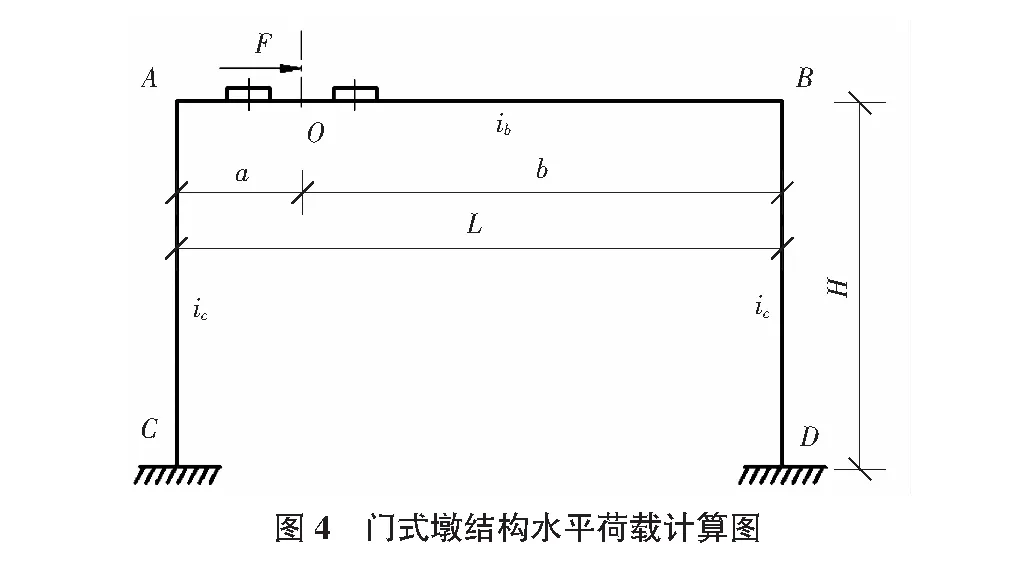
利用力法和位移法[4]计算推导得出各关键点位置的弯矩式(8)。

(8)

墩柱顶、底的轴力大小为横梁两端的剪力值，因此可以得出各关键位置的轴力式(9)。

(9)

4)基础沉降。

基础沉降主要为门式墩结构两侧基础不均匀沉降导致结构出现次内力。Δ为墩柱不均匀沉降值，如图5所示。

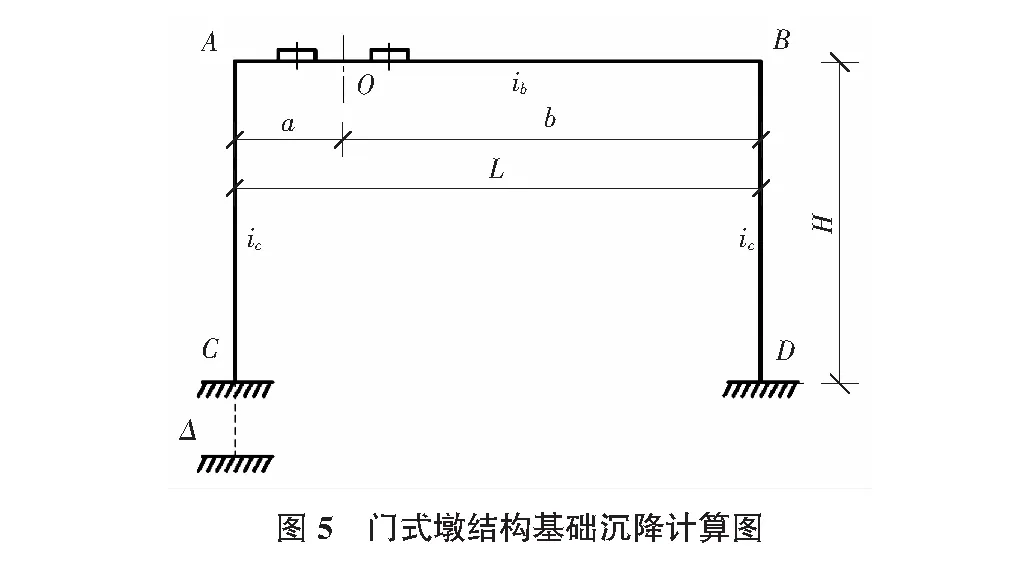
通过结构力学[4]推导得出各关键点位置的弯矩式、轴力式。

(10)

(11)

5)温度作用。

温度作用主要包括门式墩结构整体升、降温以及不均匀升温。其中，ΔT为整体升、降温度；Δt为门式墩外侧不均匀升温；αc为材料线膨胀系数。通过结构力学[4]计算推导可得出各关键点位置的弯矩，式(12)为整体升、降温作用，式(13)为不均匀升温作用，其中，hb,hc分别为横梁高度、墩柱横桥向宽度。

(12)

(13)

6)制动力。

制动力Fb属于平面外荷载，横梁按两端铰接处理，墩柱按悬臂梁结构计算。因此墩柱底平面外弯矩MC=(1-m)FbH，MD=mFbH。

7)地震作用。

首先利用等效质量法将门式墩多质点体系用单质点体系代替，使单质点体系的自振频率和原体系的基本频率相近，如图6所示。按照此法使门式墩结构近似简化为单自由度体系，墩柱质量全部集中在横梁上。

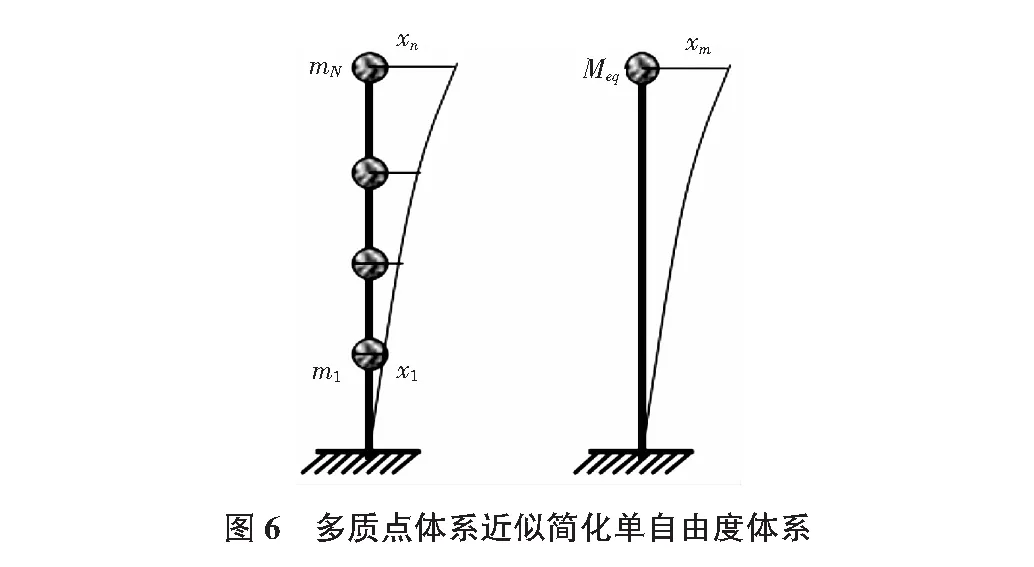
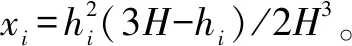
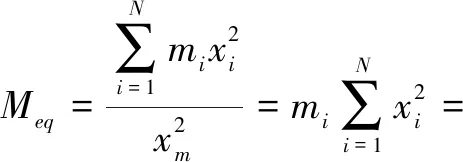
(14)

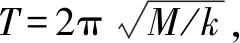
3 工程实例

新建中卫至兰州铁路为双线250 km/h客运专线，其中新建刘家湾特大桥Z38号门式墩结构采用预应力混凝土横梁，为跨越中石油天然气管道所设。横梁跨度20 m，墩柱高度17 m，如图7所示。按本文计算L=20 m，H=18.9 m，m=0.37。梁跨布置为2孔单线32 m简支箱梁，图号“通桥(2008)2211A-Ⅱ”，位于R=2 200 m圆曲线上(离心力由近荷载侧指向远荷载侧)。建设场地地震设防烈度为7度，地震动峰值加速度为0.15g，地震动反应谱特征周期0.45 s。地质以砂质黄土、泥质夹砂岩为主。

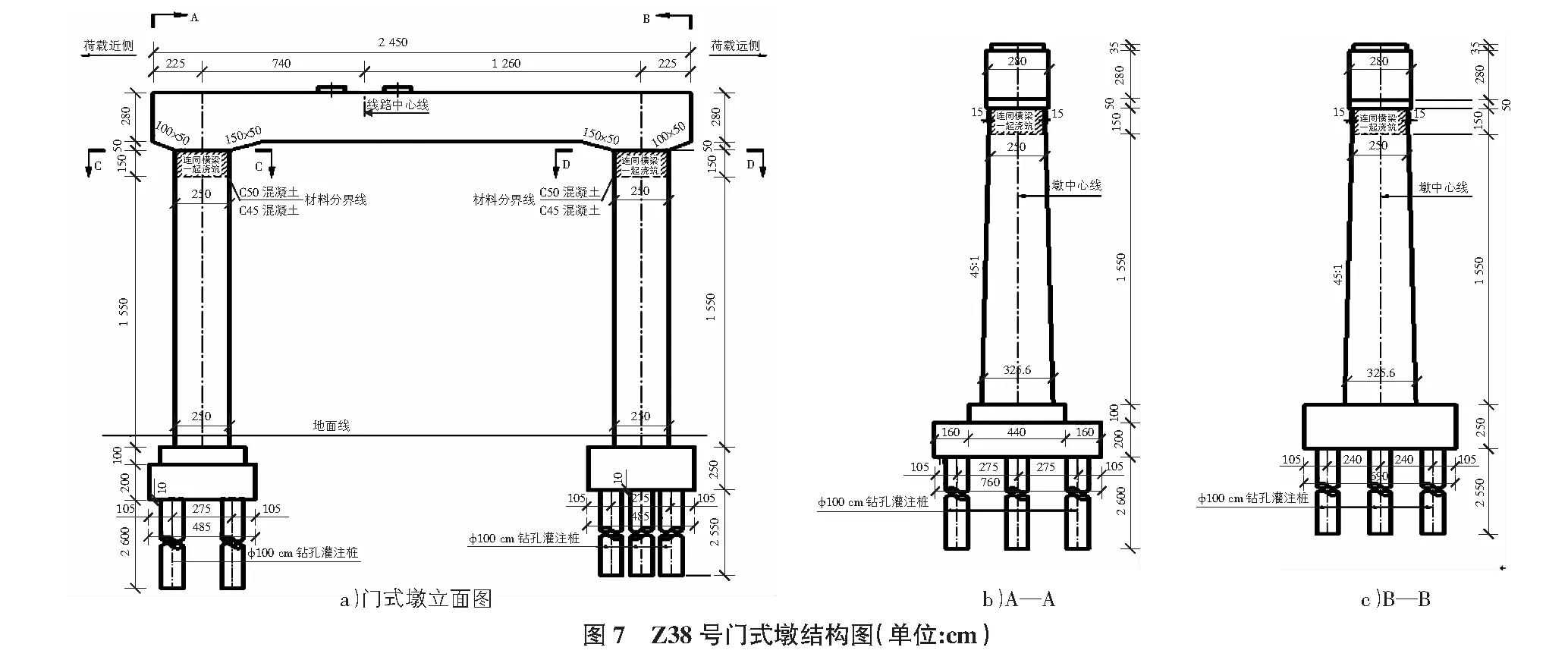
门式墩荷载信息[10]：梁部恒载(梁部自重+二恒)8 626 kN；双重活载(考虑冲击系数)2 471 kN；摇摆力100 kN；制动力240.6 kN；离心力(双重活载考虑折减系数)299.8 kN；基础不均匀沉降按1.0 cm考虑；温度按整体、升降温30 ℃；外侧不均匀升温5 ℃。

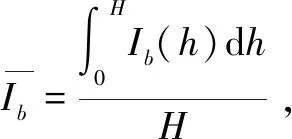
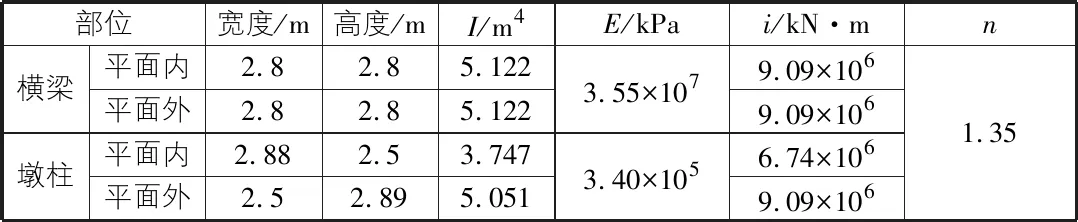
表1 门式墩结构截面几何特性

3.1 门式墩结构刚度计算对比

根据本文纵、横桥向刚度解析表达式式(2)，式(3)得出不考虑基础刚度影响的门式墩结构顺、横桥向刚度，计算结构刚度时，截面刚度应按铁路桥涵混凝土设计规范取0.8EI计算[11]。考虑到地质条件较好则k1/k2取3/2，则桥墩k纵=457 kN/cm，桥墩k横=1 090 kN/cm，均满足最小线刚度要求。

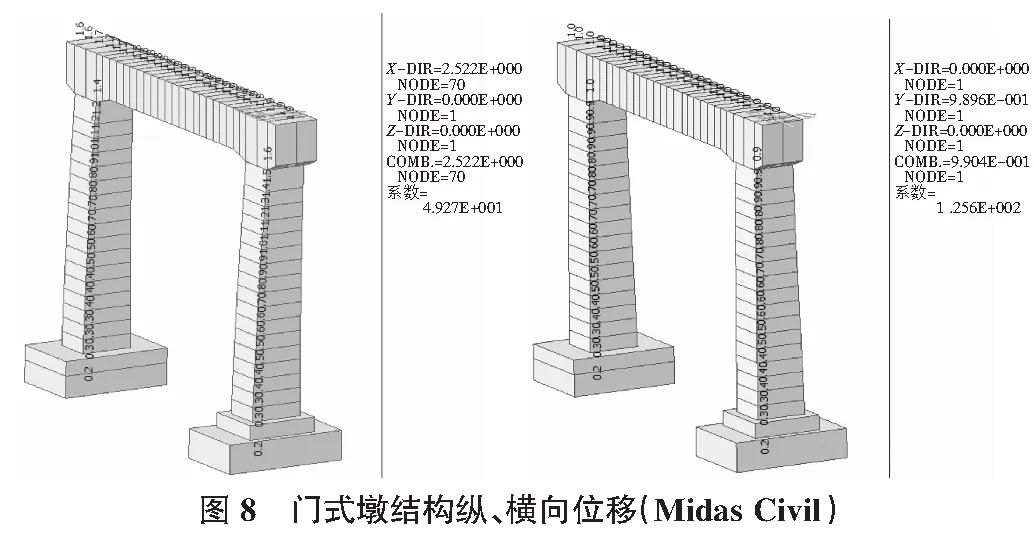
采用Midas Civil建模计算[12]，并考虑基础一般弹性支承，截面刚度取0.8EI，得出门式墩在纵横向1 000 kN作用下纵、横向位移如图8所示，得出桥墩k纵=476 kN/cm，桥墩k横=1 000 kN/cm，与简化计算结果基本一致。

3.2 门式墩结构内力计算对比

通过式(4)～式(14)内力解析表达式，计算得出门式墩结构关键截面内力，如表2所示。其中计算地震作用力时，利用式(14)得出墩柱等效质量Meq=211 t，通过桥墩纵、横向刚度(不考虑截面刚度0.8倍的拆减)得出门式墩结构纵向自振周期T1=1.053 s;横向自振周期T2=0.708 s，分别对应门式墩结构的一阶和二阶自振周期，与Midas Civil分析得出T1=1.057 s，T2=0.825 s，结果基本一致，见图9。

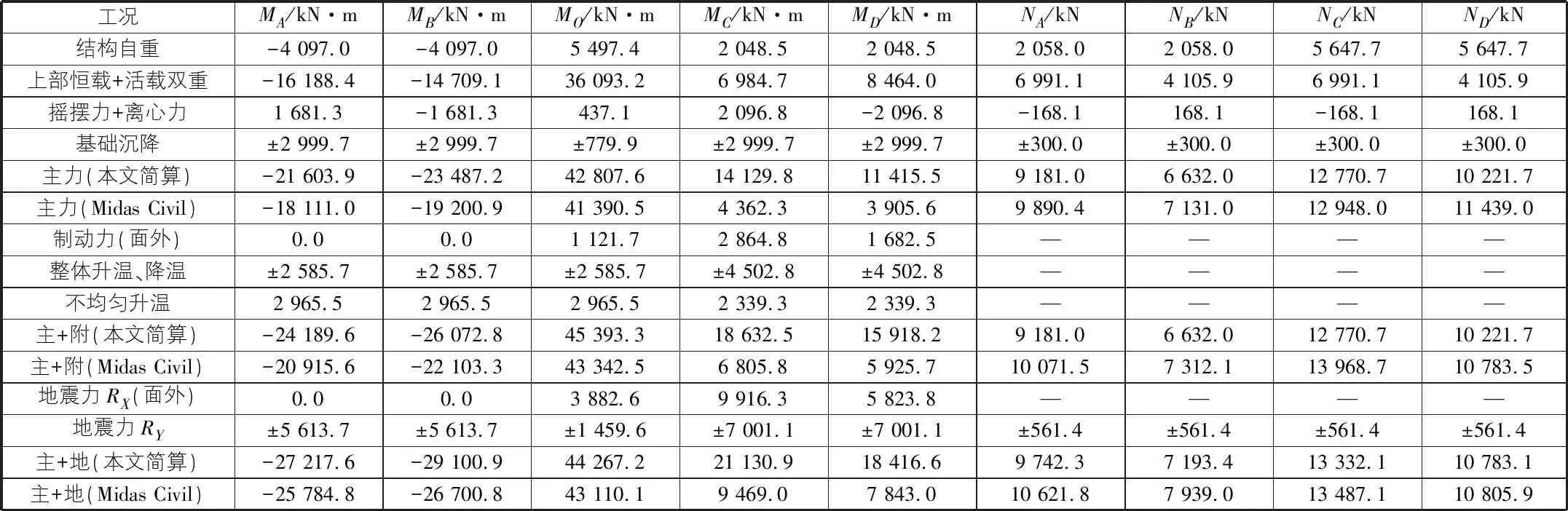
表2 门式墩结构关键截面内力

通过表2关键截面内力与Midas Civil计算结果对比发现采用本文简化计算方法得出的墩柱顶、底弯矩偏大，尤其墩柱底相差较大，这是由于简化计算模型将墩柱底完全固结导致[13]。这对于墩柱下部桩基的设计影响较大，需要适当调整墩柱底的弯矩。因此引入基础刚度影响折减系数λ，λ=0时墩柱底完全铰结，λ=1时墩柱底完全固结。基础刚度影响折减系数λ在0～1之间，需通过地质条件、桩基布置形式综合确定，本文取0.5。

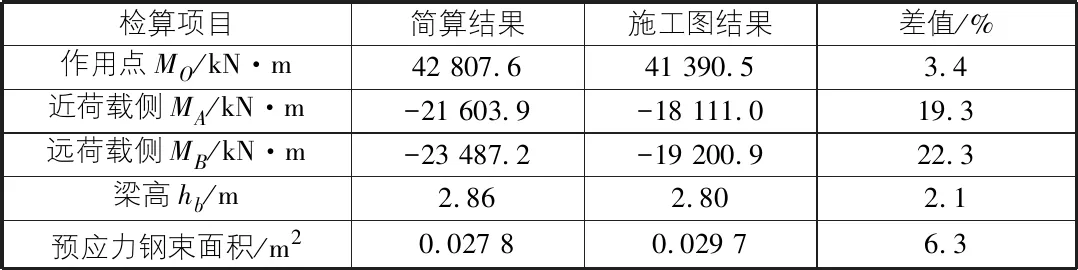
表3 横梁简化计算与施工图结果对比表

对于桩基设计[15]，还需要考虑承台重量、承台顶填土重量以及墩柱底剪力引起的承台底的弯矩，通过计算得出主+地工况控制桩基计算结果，与施工图对比如表4所示。

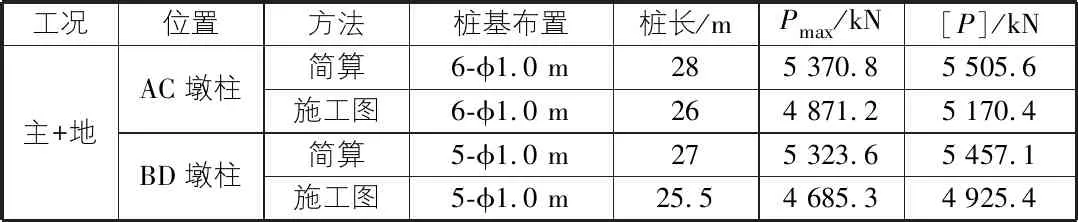
表4 桩基简化计算与施工图结果对比表

通过对比发现桩基简化计算比施工图结果偏保守。这是由于简化计算模型将墩柱底完全固结导致，使调整后的墩柱顶、底弯矩仍偏大，但是这种偏保守的设计误差还是能够接受的。

4 结论

1)利用本文推导得出的门式墩墩身纵、横桥向刚度k1解析表达式，再通过墩高和地质条件确定墩身刚度k1和基础刚度k2的比值，可以准确地得到门式墩顺、横桥向墩顶线刚度k。从而根据桥墩最小线刚度的要求确定墩柱截面尺寸以及桩基布置形式。

2)地震作用通过采用能量等效原则将多质点的门式墩结构转化为单自由度结构，能够快速、准确地计算出结构的自振周期，简化地震力计算。

3)根据门式墩结构在各种荷载作用下的内力解析表达式，通过编制电子表格按规范要求进行荷载组合，与Midas Civil设计结果对比发现：a.对于横梁两端负弯矩虽存在偏差，但不影响设计，可以通过本文简化计算快速、有效地确定横梁高度、预应力钢束面积等。b.对于桩基简化计算门式墩柱底弯矩偏大，主要原因是门式墩基础完全固结导致。故墩柱底在本文简化计算的结果上乘以基础刚度影响折减系数λ，调整后的墩柱底内力可以确定桩基根数、桩长等，从而实现门式墩结构快速设计。