基于极限平衡分析法的公路土质边坡稳定性分析

孟 泽 彬

(山西路桥集团隰吉高速公路有限公司，山西 太原 030006)

0 引言

公路土质边坡在外力荷载以及地下水运动、地震等内力作用下，边坡的内部某一位置上的滑动力超过了土质本身的抗滑力，将会失去原有的边坡稳定性。边坡失稳是一种十分严重的灾害，具有较大危险性，威胁着人们的安全[1]。由此认为，公路土质边坡稳定性分析十分必要，不仅可以找出潜藏的危险，也能够为社会经济发展提供保障。作为岩土工程中的重要研究项目，分析方法涉及到周边房屋、道路、矿山以及水利水电等诸多工程领域。影响到边坡稳定性的因素较多，因此具有不确定性，在实际分析中较为复杂，此次分析中将极限平衡分析法应用于边坡稳定性分析中，可有效提高分析计算结果的精确度。

1 基于极限平衡分析法的公路土质边坡稳定性分析方法

在设计基于极限平衡分析法的公路土质边坡稳定性分析方法时，应将传统的极限平衡理论作为基础，对公路土质边坡进行条块划分，并遵循如下原则：第一，假设边坡的稳定性安全系数为Wd，且Wd的定义应将土质的抗剪强度指标降低；第二，公路土质边坡的各垂直条块的最底侧和最外侧应当满足Tresca屈服准则和Mises屈服准则，不同的是，条块的底部处于极限破坏状态，公路土质边坡中失去稳定性的滑体与各个条块应同时满足力的平衡以及力矩的平衡条件；第三，考虑到土质边坡中含有大量的孔隙，因此，进行极限平衡分析时，要将孔隙中的水压力、地震力以及外界荷载造成的影响进行综合的考虑[2]。

1.1 构建边坡受力模型

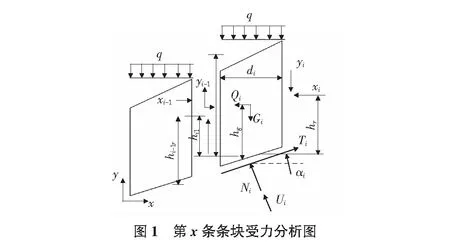
在构建边坡的受力模型前，首先要按照通用条分法的基本原理对公路土质边坡进行划分。再通过构建边坡受力模型对边坡的稳定性进行分析[3]。将公路土质边坡中失去稳定性的滑动体从左到右划分为m条垂直条，从中选取第x条进行受力分析。图1为第x条条块的受力分析图。

图1中Ti为第x条条块的底部切向阻力；Qi为水平方向的地震力；Gi为条块自身的重量；Ni为条块底部的有效法向力；Ui为条块底部的孔隙水压力；xi-1和xi为条块左右两侧水平条间力；yi-1和yi为条块竖直方向上的相互作用力；αi和di分别为条块的底部坡角和条块宽。由于滑动部位的面积、形状已知，因此对条块进行划分后，条块的底长、宽、中心平均高度、底部坡角等参数均可确定。对于整体公路土质边坡而言，需求解出的未知量为：每条条块的底部切向力以及有效法向力；相邻两个条块分界面上的法向条间力和切向条间力；条块两侧法向条间力到公路土质边坡底部的中心位置距离；公路土质边坡的安全稳定系数，本文设计的分析方法假设每块滑体与整个公路土质边坡的安全稳定系数均相同。

1.2 确定极限平衡分析方程

根据需要确定静止状态下，公路土质边坡的极限平衡分析方程：

第x条条块底部切向力方向平衡方程：

Ti-(xi-xi-1)cosαi-Qicosαi-(yi-yi-1)sinα=0

(1)

第x条条块底部有效法向力方向平衡方程：

Ni+Ui+(xi-xi-1)sinαi-(yi-yi-1)cosαi=0

(2)

式(1)，式(2)中各物理量含义与图1相同。

为了方便后续求解出公路土质边坡的安全稳定系数，按照常用思维逻辑将假定进行简化。主要从以下方面进行：

第一，简化后的假定应满足公路土质边坡的力学特征，以及条块的合理性要求，划分条块的侧面剪应力不能超过该条块上表面的最大抗剪强度，即Fv>Fs，其中，Fv为条块沿垂直方向上的安全稳定系数；Fs为划分条块的侧面剪应力，此时条块侧面并未达到极限平衡的状态。

第二，垂直方向上的条块间没有相互作用力，边坡所受作用力的合力，垂直于边坡内侧。根据Tresca屈服准则和Mises屈服准则，边坡滑动面上的安全稳定系数应为：边坡抗剪强度指标降低与安全系数相同数值的倍数后，边坡的滑动面处于极限平衡状态。

第三，以通用条分法结合边界约束条件，对边坡边界条件的数值进行提取，当条块宽度到达极限最小值时，边坡端点两侧作用力的合力与条块顶点相平行，并确保边坡滑动面两端点的外侧应力与力矩的取值为0。

以极限平衡方程计算条块间应力，发现条块与条块间的作用力较多，所以，在实际分析过程中，应着眼于作用力相关的量。以Tresca屈服准则和Mises屈服准则作为理论基础，设边坡条块间的切向力与垂直作用力在边坡滑动面上的法向力具有线性关系。分析边坡滑动面的实际受力情况，经分析发现，滑动面的受力包括条块侧面的剪切力，以及条块所受的法向力，二者的力共同作用于边坡应力圆上，具体的受力分析如图2所示。

由此可得出土质边坡中条块之间的相互作用力存在的关系为：yi=kxi，其中，k为作用力间的系数，为变量，且k的取值在每一条划分的条块中的数值均不相同。

1.3 设计数值分析步骤

数据分析具体步骤为：根据公路土质边坡的具体情况进行分析，选择对应的最简方法确定整个边坡的安全稳定系数的迭代初始数值，从左至右依次进行计算；按照上文确定的平衡公式求解出第二条块的各项参数数值，再以第二块条块为基准，求解出下一条块的各项参数数值，以此类推直至最右端的条块数据计算完成。对于公路土质边坡而言，在分析时需满足力的平衡，若不满足，则需要对划分条块的侧面剪应力进行调整，直至满足力的平衡要求，获取相应的曲线关系；将力矩平衡与上文平衡公式结合得出第二条块的各项参数数值，再以第二条块作为基准推导出下一条块，同理得出最右侧的侧边值。

2 实验论证分析

2.1 实验准备

首先，利用SLIDE仿真软件构建一个完整的模拟公路土质边坡，并设定边坡相应的参数数据：边坡坡角为23.84°，边坡坡长1 350 m，边坡坡宽450 m，边坡坡高65 m。分别利用两种稳定性分析方法对该模拟公路土质边坡的稳定性进行5次分析，设置对照组为传统稳定性分析方法，实验组为本文设计的稳定性分析方法。为了确保实验的准确性，实验应符合单一变量原则。

2.2 实验结果及分析

将实验过程中产生的数据信息：安全稳定系数、分析结果误差等进行记录,如表1所示。

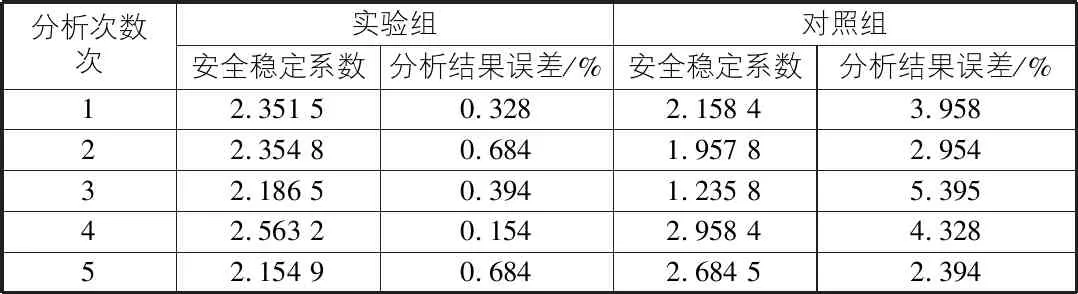
表1 实验组与对照组实验结果对比

通过实验及表1中的数据可知，通过实验数据可知，实验组的稳定性分析结果误差明显低于对照组，且由表1中第3次分析可以看出，对照组的分析结果误差大于5%，不符合稳定性分析误差范围在5%的要求，而实验组的分析结果误差均小于1%。因此，通过实验证明，本文设计的稳定性分析方法的精准度更高，更适用于实际的应用中。

3 结语

本文通过将极限平衡分析法结合到公路土质边坡稳定性分析中，通过对比实验证明了该方法的可行性。但该方法的不足之处在于，只能在设定好的边坡滑动面上进行分析计算，若对边坡进行最危险滑动面的搜索需要进行更多的试算，降低了分析方法的效率同时使分析过程更加复杂。因此，在日后的研究中还将对这一方面问题进行更加深入的研究。