基于ARMA-GARCH-M 模型的沪深300 指数波动研究

王毅 同济大学

一、文献综述

经验证明金融波动率随时间变动，即B-S 模型的第一个假设中的常数波动率与实际情况并不相符。Engle（1982）在《计量经济学》的一篇论文中提出了ARCH 自回归条件异方差模型，为波动率建模开创了系统框架。该模型的提出也为Engle 赢得了2003 年诺贝尔经济学奖。其基本思想为：收益率的扰动at虽然序列不相关但并不独立，且这种不独立可用延迟值的简单二次函数来刻画。充分描述数据的波动率过程用ARCH 建模时往往需要较高的阶，这增加参数估计的难度，进而最终影响模型拟合精度。为了解决这个问题，Bollerslev（1986）在他的老师Engle 的成果的基础上，提出了GARCH 模型。金融资产收益率常常会依赖其波动性，为刻画该现象，Engle（1987）提出应把风险引入到均值方程以反映风险溢价，Chou，R.F.（1988） 构 造 出GARCHM（GARCH in the mean）模型。此后，几乎所有自回归条件异方差领域的新成果都是基于GARCH 模型。Nelson（1991） 的指数 GARCH，Glosten，Jagannanthan 和Runkle（1993） 及 Zokoian（1994） 的 门 限GARCH 等等，不断在其基础上衍生、拓展、改进，以求更好的描述数据波动性特征。

二、研究方法和步骤

本文选取沪深300 指数作为研究对象，Campbell，Lo 和MacKinlay（1997）认为：一方面，资产的投资机会完全由其收益率体现，与投资规模并没有关系；另一方面，收益率序列具有更加良好的统计性质，相对价格序列更易处理。因此多数金融研究针对的是资产的收益率，而非其价格。

本文将资产的简单毛收益率取自然对数处理，即可得到对数收益率，也叫连续复合收益率。当面对多期收益率等问题时，对数收益率rt较之简单收益率Rt具有更容易处理的统计性质。我们记pt= lnPt，通过简单的推导，有：

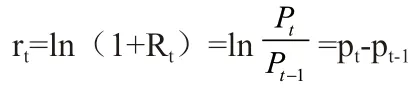
本文把通过Wind 金融终端获取的沪深300 指数每日收盘价视为其“资产价格”，先取对数再进行差分获取相应对数收益率序列，并以此为样本数据进行后续实证研究。

收益率序列基本围绕零在波动，波动幅度不一致，07 年至09 年初、14 年下半年至15 年两个时段波动性较强，其余时间波动性相对而言较弱。这也印证了前述分段处理的合理性和准确性，说明它成功地区分了市场的平稳时期和极端时期，为后续更好地建模打下基础。

一个收益率序列建模需如下三个步骤：1.检验相关性并建立均值方程，如有必要，通过ARMA 等模型消除线性依赖2.对上一步模型的残差进行ARCH 效应检验3.若上一步ARCH 效应显著，再建立波动率模型，对均值方程和波动率方程进行联合估计4.对模型拟合效果进行检验。本文按这样的顺序对数据进行处理，探索沪深300 指数收益率序列更多的性质与特征。

三、研究结论和意义

本文通过实证检验得到沪深300 指数对数收益率序列的分布无论在整体研究期还是细分时段都不满足传统正态性假设，表现为左偏和尖峰厚尾。从收益率时间图还可看出序列波聚现象明显。

本文采用的误差项服从NIG 分布的ARMA-GARCH 模型较好地刻画了沪深300指数波动特征，消除序列自相关性与异方差性的效果良好。实践证明，GARCH（1，1）拟合效果最佳，在普通序列研究中最为常用不无道理，阶数升高易导致系数不显著。另外，5 个模型拟合出的ARCH 参数与GARCH 参数都满足和小于1 但非常接近1，揭示了收益率的条件方差序列具有平稳性，模型可测，A 股受外部冲击产生的波动具有持久性，即长记忆性特征明显。

根据模型拟合结果，A 股从整体研究期看，风险溢价效应并不显著。但分时段再看，就会有新的发现。剧烈震荡的金融危机时期和1415 大起大落时期archm 系数皆同样不显著；但在比较平稳的金融危机前期和金融危机后期，收益具有明显的正的风险溢价。这说明我国股市还是不够成熟，与选择好标的分享企业的发展与成长的理念相左，在市场平稳时“耐不住寂寞”，投机性交易多。