基于动态闭环反馈的信号交叉口车速引导方法
王文辉,吕小磊,彭 峰,褚端峰
(1.武汉理工大学 人事处,湖北 武汉 430070;2.东风汽车公司技术中心,湖北 武汉 430056;3.武汉理工大学 智能交通系统研究中心,湖北 武汉 430063;4.武汉客车制造股份有限公司,湖北 武汉 430200)
随着我国经济的快速发展,人民生活水平的不断提高,居民汽车保有量持续增加,导致城市交通拥堵现象日益严重,而道路信号交叉口控制区域则决定了城市道路的整体通行能力。在信号交叉口的车路协同系统中,基于车载设备获取的交通信息和车辆行驶信息,结合车速引导模型给予车辆动态的速度引导,有利于减少车辆不必要的加减速、怠速和启停等行为,提高信号交叉口处的车辆通行效率。
目前,国内外已经有学者对信号交叉口的车速引导方法进行研究。如ASADI等[1]设计了一种基于交通信号的车速引导模型,车辆以参考速度行驶并保持车辆之间的安全距离,可减少车辆制动时间,及时在绿灯期间到达信号灯交叉口。为了可以平滑地跟踪ASADI等提出的参考速度,BARTH等[2]提出了一种三角函数速度优化模型来提前调整车速,使车辆在不停车的情况下通过信号交叉口。WAN等[3]以提高燃油经济性和通行效率为目标,通过交通信号预测系统计算燃油经济性次优解的车速咨询系统,并证明了该系统不仅提高了自身的燃油经济性,还对其他常规车辆有一定的经济效益。YANG等[4]开发了一种ECACC算法,该算法通过对交叉口队列的估计计算最优车速轨迹。HAN等[5]以最小车距和最大道路限速作为状态约束,以能耗作为最优函数推导出实时的速度分布图,该系统在不增加行车时间的前提下,能显著降低能量消耗,避免碰撞。ZHAO等[6]提出了一种基于队列的协同生态驾驶模型,并证明自动驾驶车辆与普通车辆的协同能够降低整个交通系统的油耗。HUANG等[7]将交通状态预测(以求目标车速)、生态驾驶车速控制和动力传动系统控制相结合,形成了一个生态驾驶系统,在不同的交通场景下都表现出了鲁棒性。
但上述研究主要集中于自动驾驶环境中的生成速度优化曲线上,忽略了驾驶员对引导车速的响应能力。同时,自动驾驶技术尚未完全普及,这使得车速引导系统的适应性较低。因此,笔者以现有的三角函数优化车速引导模型为基础,考虑到驾驶员在实际驾驶时无法完全跟踪速度引导曲线,设计了一种闭环反馈的车速引导方法,以动态补偿人车响应特性造成的跟踪偏差,提高车速引导系统对驾驶员的适应性。
1 基于动态闭环反馈的车速引导方法
信号交叉口处单车的车速引导模型主要为在近信号控制区的驾驶员提供引导速度。结合实际行驶情况,笔者做出如下假设:
(1)在行驶过程中不存在行人与非机动车的影响;
(2)以单个交叉口为研究对象;
(3)主要引导车辆直行,不考虑换道情况;
(4)《道路交通安全法实施条例》规定,黄灯亮时已越过停止线的车辆可以继续通行,还未越过停止线的车辆应停车。因此,将黄灯亮时看作禁止通行,将黄灯时间看作红灯时间。
1.1 车辆通行预判模型
在道路交叉口,由于信号灯的影响,车辆在近信号控制区主要存在加速、匀速、减速和停车4种操作行为。车速引导模型首先需要结合信号交叉口处的交通信息和自身车辆信息,计算出最优引导车速区间,并判断车速是否需要调整,即构建车辆通行预判模型。车辆通行预判模型的构建步骤为:
(1)在进入近交叉口信号控制区时,车载设备接收到路侧设备发送的信号灯相位信息MSPAT、红灯/绿灯剩余时间tr或tg和信号交叉口的位置,根据自身车辆的位置信息,计算出车辆到达信号交叉口的距离dint。基于车辆初始速度v0,由式(1)计算车辆到达信号交叉路口的时间treach。
(1)
(2)在treach时刻,若信号灯相位变为绿灯,则车辆匀速通过。
(3)在treach时刻,若信号灯相位变为红灯,则需要判断此时信号灯的相位信息。若当前时刻的信号灯为红灯,则判断车辆是否可以采用减速不停车的方式通过交叉路口。若当前时刻的信号灯为绿灯,则判断是否可以加速通过。假设车辆在绿灯剩余时间tg内,以最大加速度amax加速到道路最大限制速度vlim行驶,通过式(2)计算车辆在时间tg内行驶的路程d。若d>dint,则车辆可以采用加速不停车的方式通过交叉路口;否则,转至步骤(4)。
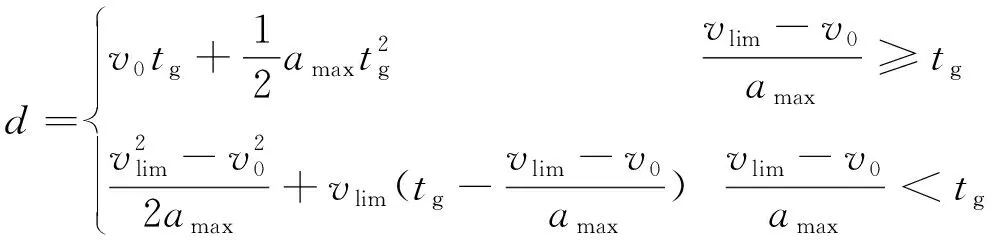
(2)
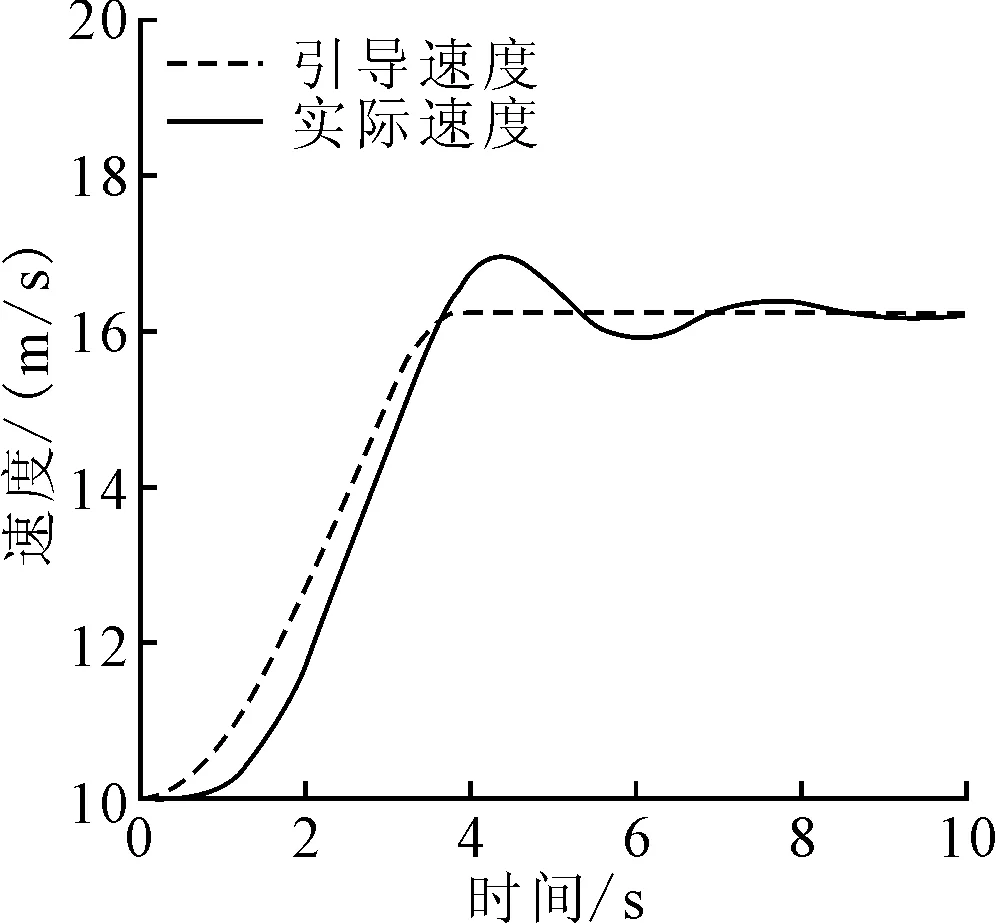
(4)判断车辆是否可以采用减速不停车的方式通过交叉路口。假设车辆减速到不影响道路交通的道路最低行驶速度v′lim,通过式(3)计算车辆在第二次绿灯亮起的剩余时间t′g内行驶的路程d′。若d′ (3) 其中,amin为最小减速度。 基于上述车辆通行预判模型,为了实现平稳节油的车速引导,文献[2]提出三角函数优化方式实现加减速优化,如式(4)所示。 vopt(t)= (4) 式中:vopt(t)为t时刻基于三角函数优化后的车辆速度;va为车辆的平均目标车速;vd为车辆平均目标车速与初始车速v0之差;ω为当车速介于当前速度vc与平均目标车速va之间时的加速/减速的变化率;φ为车辆速度低于平均目标车速va时的加速/减速的变化率;tf为目标距离与平均目标车速va的比值。 综合以上方程,建立约束方程组: (5) 式中:J为加速度变化率,其不能超过一定的值;amax为最大加速度,其值不得超过2.5 m/s2;约束条件φ=max{φ}表示为尽快使车辆速度在加减速阶段达到匀速,尽可能取φ的最大值。 上述模型生成的速度引导曲线是按照绿灯开始或结束时刻车辆正好通过交叉路口的要求生成的。在实际情况中,当车辆速度高于引导速度时,会产生车辆到达路口绿灯还未开始的情况。当车辆速度低于引导速度时,会产生车辆到达路口绿灯已经结束的情况。针对上述两个问题,笔者对上述模型进行改进。 考虑到驾驶员不能完全按照所提示的最优速度曲线行驶,通过对实际速度轨迹的反馈,动态更新速度引导曲线,建立闭环反馈速度模型,确保驾驶员可以在绿灯时间不停车通过信号交叉口。闭环反馈车速引导系统将车辆实际行驶速度vact实时反馈给速度优化模型作为输入,速度优化模型随之动态更新最优目标速度vopt。 文献[2]所提出的速度优化模型(见式(4))在生成速度引导曲线时,开始时刻的加速度为0。在反馈过程中,车辆的实际加速度不为0。因此,将vd用加速度、速度与时间的函数来表示,得到调整后的速度优化曲线和约束方程,分别如式(6)和式(7)所示。 vopt(t)= (6) (7) 为了避免更新过于频繁,同时保证更新阶段具有足够的更新时间,消除人车响应时延的影响,保证车辆不停车通过交叉路口。笔者以绿灯剩余时间为参考,将更新步长设定为绿灯剩余时间的一半。根据刘运通等[8]的调查结果,驾驶员的平均反应时间为1 s。为了满足所有驾驶员的需求,将最小更新步长设为2 s,即当绿灯剩余时间小于4 s时停止引导速度曲线的更新。 文献[8]的研究表明,驾驶员在跟踪动态目标时的波动性和控制领域中的PID(proportion integration differentiation)控制十分相似。PID控制中的比例参数、微分参数和积分参数可以分别表示驾驶员对当前速度误差、累计误差和误差变化率的反应程度。因此,笔者采用PID控制来模拟驾驶员跟踪最优速度曲线[9-10]。车辆的响应模型采用以下一阶响应模型来表述: (8) 将式(8)改写成传递函数的形式: (9) 根据实际车速vc(t)与引导速度vopt(t)的偏差,驾驶员通过改变u(t)来改变车辆行驶速度进而减小速度偏移量,经过循环反馈不断改变车辆行驶速度vc(t)直至通过交叉路口。其中,s为拉普拉斯算子,U(s)为u(t)的拉普拉斯变换。 PID控制的数学表达式为: 式中:e(t)=vopt(t)-vc(t) ;kp、ki、kd分别为比例控制参数、积分控制参数和微分控制参数。 同样将式(10)改写成传递函数的形式: (11) 结合式(9)和式(11)可得vc(s)与vopt(s)的关系式: 为了简化计算,将比例控制参数kp、微分参数kd和积分参数ki设置为定值,即kp=5、kd=5、ki=5。 基于Matlab的Simulink环境对上述车速引导模型进行仿真。所有仿真实验在同一驾驶工况下进行:未到达交叉路口停车线的部分为车速引导部分,长度为100 m;停车线后为自由行驶部分,长度为50 m。车辆以10 m/s的初始速度驶入车速引导区域,绿灯和红灯的周期时长均为20 s,道路限速vlim为20 km/h。仿真工况示意图如图1所示。 图1 信号交叉口车速引导仿真工况示意图 基于三角函数车速引导模型和基于闭环反馈车速引导模型的速度跟踪曲线分别如图2和图3所示,虚线为车速引导系统生成的引导速度曲线,实线为人车响应模型跟踪速度引导曲线生成的实际速度曲线。由图2和图3可知,车辆并不是完全按照车速引导曲线行驶的。在三角函数车速引导模型下,车辆的实际行驶速度围绕引导速度上下震荡,从而使车辆不断地处于加速和减速切换的状态;在闭环反馈车速引导模型下,车辆仅通过先减速后加速两种方式,更符合车辆的实际行驶情况。 图2 基于三角函数车速引导模型的速度跟踪图 图3 基于闭环反馈车速引导模型的速度跟踪图 图4 两种车速引导下的车辆跟踪时空图 两种车速引导下的车辆跟踪时空图如图4所示,可以看出车辆在闭环反馈车速引导模型下7 s时行驶的距离大于100 m,即车辆可以在7 s内通过信号交叉口。而三角函数车速引导模型在7 s时行驶的距离小于100 m,需要等待下一个绿灯。这表明闭环反馈车速引导模型相对于三角函数车速引导模型可以提前到达信号交叉口,即相较于三角函数车速引导模型,闭环反馈车速引导模型提高了通行效率。因此,所提出的闭环反馈车速引导模型相对于三角函数车速引导模型来说,提高了系统的适应性,保证车辆在既定时间内不停车通过信号交叉口。 笔者对车路协同系统下信号交叉口处车速引导模型进行改进,构建了基于动态闭环反馈的车速引导模型对车辆的速度和加速度进行动态反馈更新,该模型不仅可以有效提高道路交叉口处的通行效率,还可以增强系统对驾驶员的适应性。1.2 基于三角函数的车速引导模型
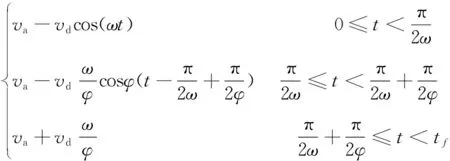
1.3 基于闭环反馈的车速引导方法
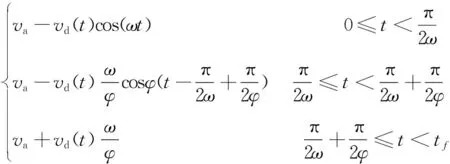
2 车速引导仿真实验设计

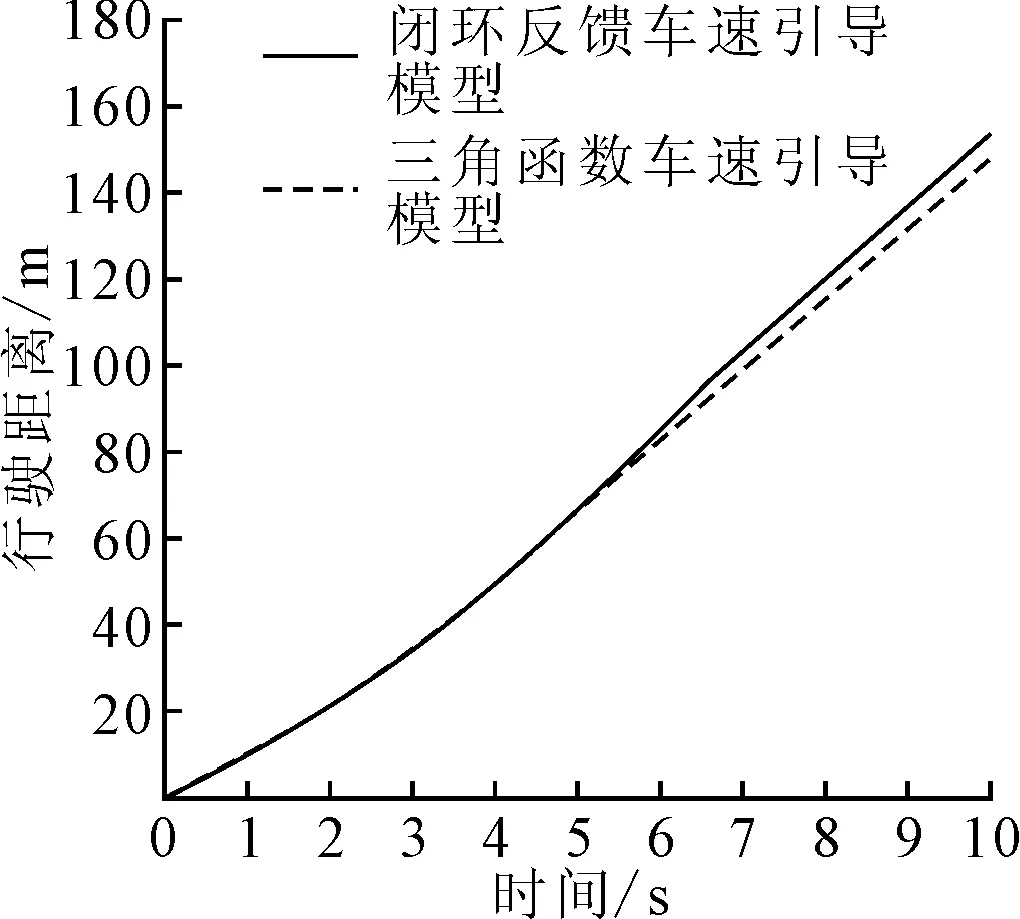
3 基于闭环反馈的车速引导仿真分析


4 结论

