基于改进型遗传算法的危险气体多泄漏源定位研究

王 吉，张 儒，李俊明

(1.中国石油大学(北京) 机械与储运工程学院，北京 102249；2.清华大学 能源与动力工程系，北京 100084)

近年来，关于危险气体泄漏事故的报道屡见不鲜，泄漏所引发的火灾、爆炸、中毒事件对人们的生命财产安全构成了极大的威胁。在泄漏事故发生后，需要利用有限的信息、采用科学的方法快速定位泄漏源并给出泄漏强度等信息，为应急响应决策提供技术支持。利用泄漏扩散场中的危险气体浓度传感器信息，采用计算机搜索定位泄漏源，称这一过程为“源强反算”，是危险气体泄漏事故应急响应任务的技术基础。某一区域发生的泄漏事故可能只有一个泄漏源，也可能有多个泄漏源。多源泄漏会明显增加源强反算的难度，尤其是当多个泄漏源产生的浓度场高度重叠时，有效区分并定位这些泄漏源就十分考验算法的能力。

在早期，学者们针对单源泄漏场景开展了一系列源强反算的算法探讨，包括模式搜索[1]、模拟退火[2]、遗传算法[3-4]等。其中，遗传算法因其并行运算能力、良好的鲁棒性和较高的运算效率获得了较多关注，针对源强反算问题也有学者提出了许多改进策略。针对多源泄漏的源强反算问题，由于多源定位势必引起优化求解问题的维度增加，故学者们考虑先找到方法进行降维，降维后再采用尽量简单快速的算法进行搜索，如最小二乘法等。HAUPT[5]采用最小二乘法结合伴随方程搜索多个泄漏源，但该方法需要对每个传感器进行伴随扩散方程的求解。LUSHI等[6]采用一种线性最小二乘法计算已知泄漏位置的4个泄漏源的气体泄漏强度，由于位置已知，大大降低了算法计算的复杂度。SHARAN等[7]则采用最小二乘法对多个泄漏源的位置和泄漏强度进行计算，并引入伴随方程对每一个传感器进行伴随扩散场的模拟。SINGH等[8-9]基于最小二乘法和改进的传感器伴随方程，对存在障碍物的扩散场内进行多个泄漏源的定位研究。ALBO等[10]基于数学推导提出了一个切向最小化算法，用于判断泄漏源的数目、位置和强度，但该方法对多个泄漏源的预估表现并不太好。总之，以上方法的实现均需要设计多源定位问题的降维方法，算法的鲁棒性还有待提高。

遗传算法应用于单个泄漏源的定位已有较多的研究积累[11-13]，然而用于多泄漏源定位问题却不十分成熟。ALLEN等[14]在遗传算法的基础上，加入一种SCIPUFF伴随扩散方程进行多源泄漏的定位，但该研究主要侧重于伴随方程的设计。ANNUNZIO等[15]采用一种基于拉格朗日推导的“多群体物理场近似”方法，使得遗传算法能够用于多个泄漏源的数量、位置预估，但计算时需要不断提出假想的泄漏源并进行判断，计算效率降低。CANTELLI等[16]将泄漏场离散为多个点，采用遗传算法实现4个泄漏源的位置和泄漏强度的计算，该方法本质上是一种多源问题的降维操作，定位精度取决于泄漏场的离散点密度。现有的遗传算法对于多源问题的求解还不太成熟，需要降维操作，会造成定位精度的下降。另外，多源问题的求解还需要遗传算法拥有较大的初始种群数量，这意味着需要更多的计算资源。

综上可知，针对多个泄漏源的源强反算问题，算法层面的工作还不够完善。鉴于此，笔者将对传统遗传算法进行改进，针对多个泄漏源采用序列定位的方法实现泄漏位置搜索，并分析泄漏源的相对位置、测量误差对算法定位成功率的影响。

1 研究方法

1.1 泄漏场景模拟

为了进行算法测试，构建二维开放空间内多个泄漏源释放危险气体后形成的浓度分布场。危险气体的扩散过程采用高斯烟团模型计算获得，扩散场内不同位置的危险气体浓度为多个泄漏源产生的浓度叠加：

(1)

(2)

图1 一个三源泄漏浓度场

以上方程也作为遗传算法求解过程中的正向浓度场计算模型。由以上方法模拟得到一个三源泄漏浓度场，如图1所示。泄漏场中还布置了多个浓度传感器，按照21×21均匀分布在1 000 m×1 000 m的扩散场内。浓度传感器的敏感度为10-6g/m3，这意味着只有当传感器位置的浓度值大于10-6g/m3时，传感器才能探测到浓度信息。定位过程中，风速和风向均为已知条件，即风沿着x轴方向吹入扩散场，风速为2.0 m/s。

1.2 遗传算法改进

传统遗传算法应用于多泄漏源定位问题，容易产生早熟收敛，算法找到了局部极值而非真实泄漏源。为了避免这一问题，一般采取扩大初代种群规模或者提高种群变异率，以迫使种群搜索更广的范围。然而，前者会增加相应的计算成本，后者具有一定的随机性，无法高效地确保遗传算法的全局搜索能力。因此，为提高遗传算法的全局搜索能力和收敛速度，对遗传算法进行如下改进：①将每次个体评价后被淘汰的个体收集到“淘汰者基因库”，当种群最优个体依然还在更新时，从淘汰者基因库中随机选取一个个体使其有一定概率参与交配；②当种群最优个体更新停止Smax代以上时，认为算法进入快速收敛阶段，这时使一部分个体向最优个体靠拢，另一部分个体与最优个体交配进行局部更优值的搜索。

改进遗传算法(modified genetic algorithm，MGA)中，每个个体即为假想的一个泄漏源，其坐标位置为(x0,y0)，泄漏的质量流量为Q0。由这个假想的泄漏源所产生的假想扩散浓度场由式(1)计算获得，个体的评价指标即为所有浓度传感器位置假想浓度值与测量浓度值的偏差：

(3)

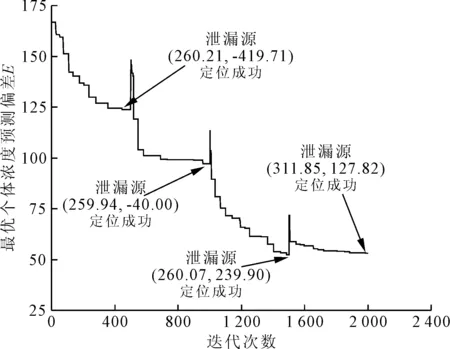
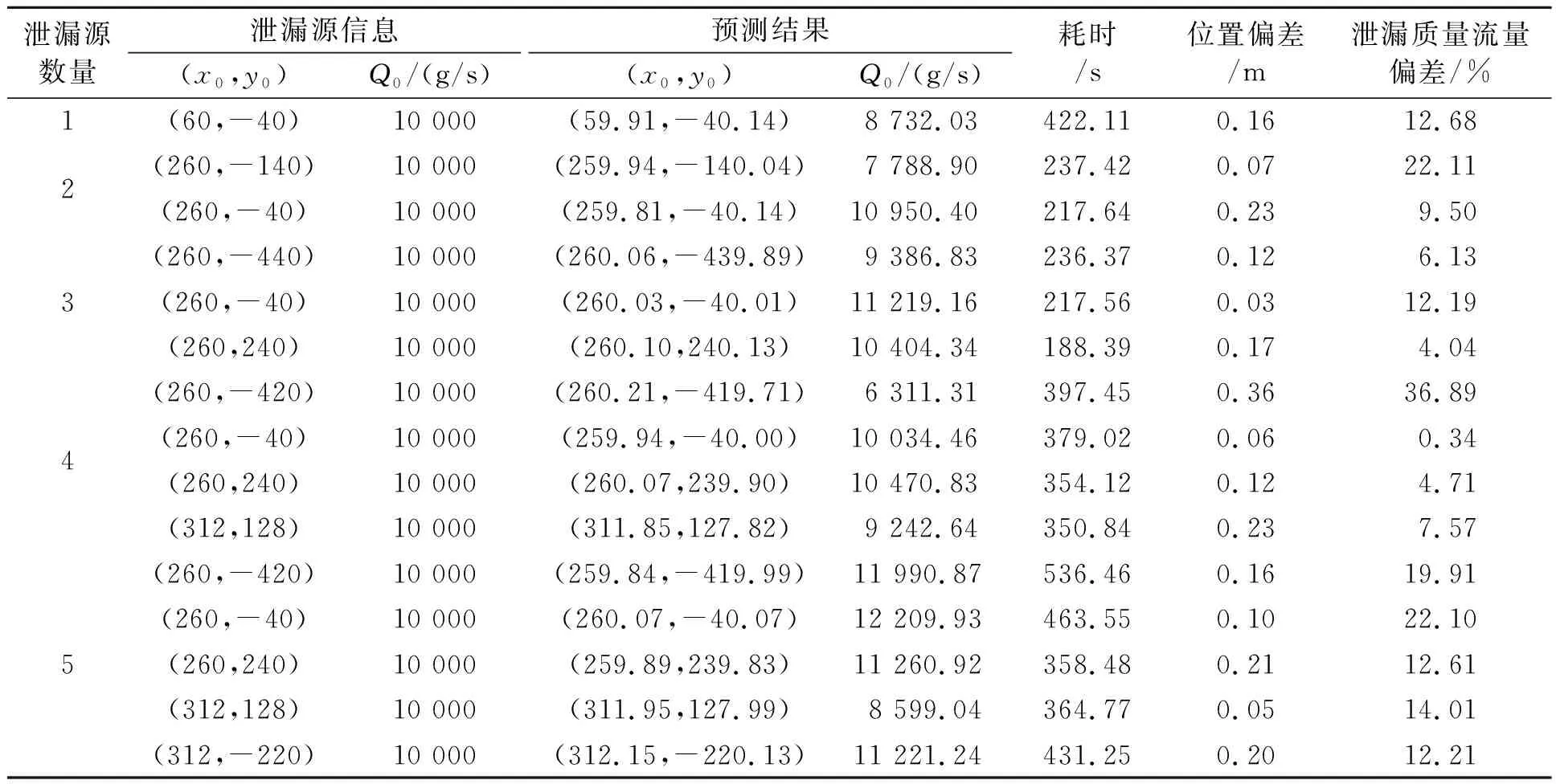
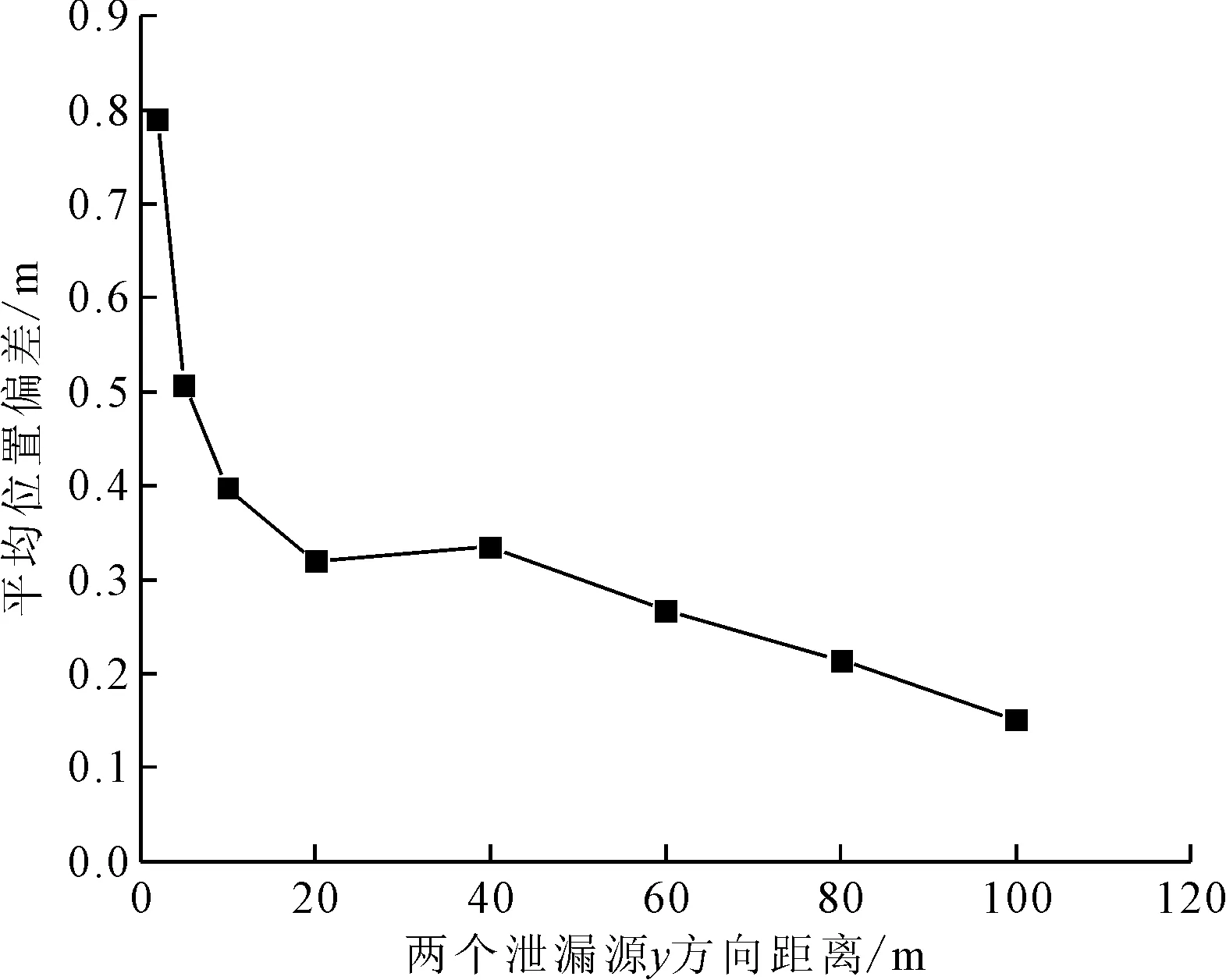
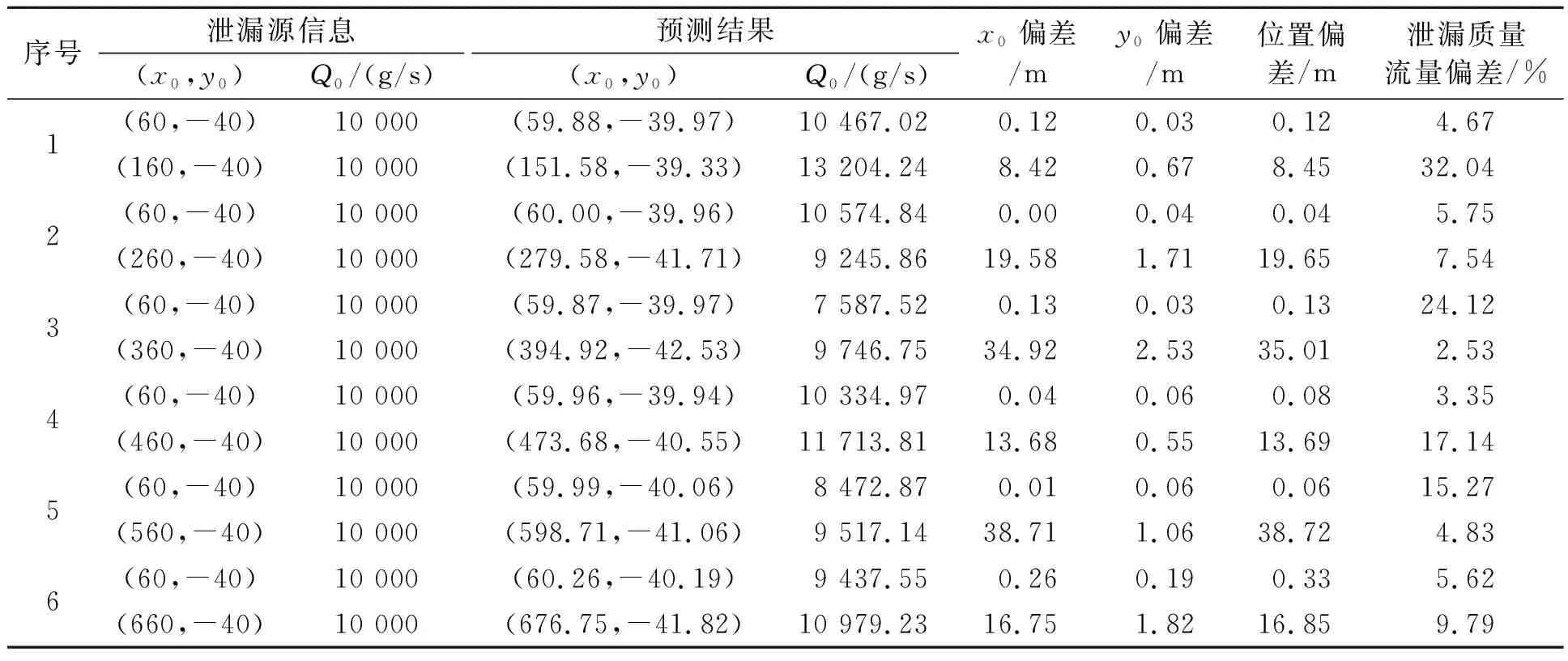
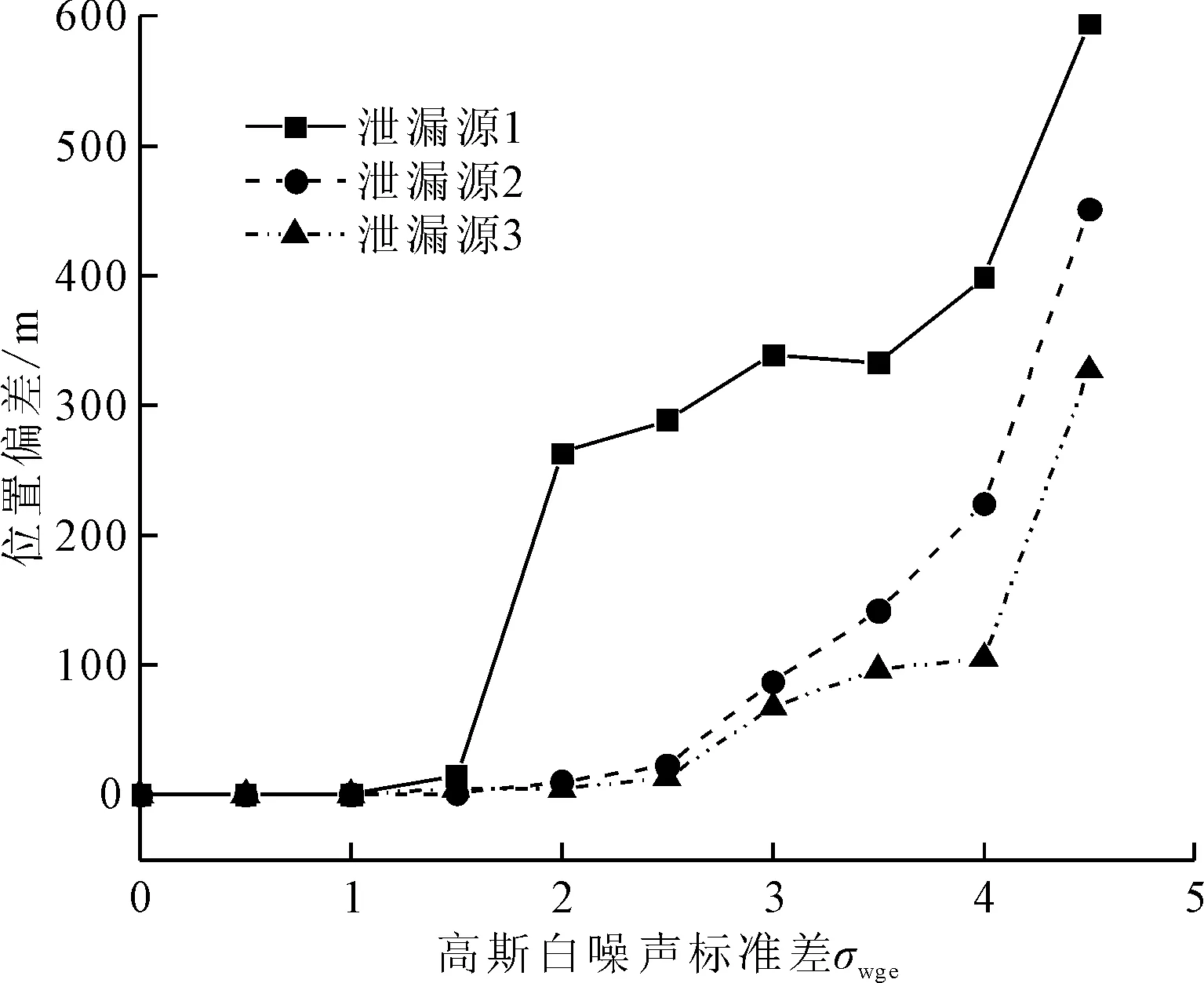
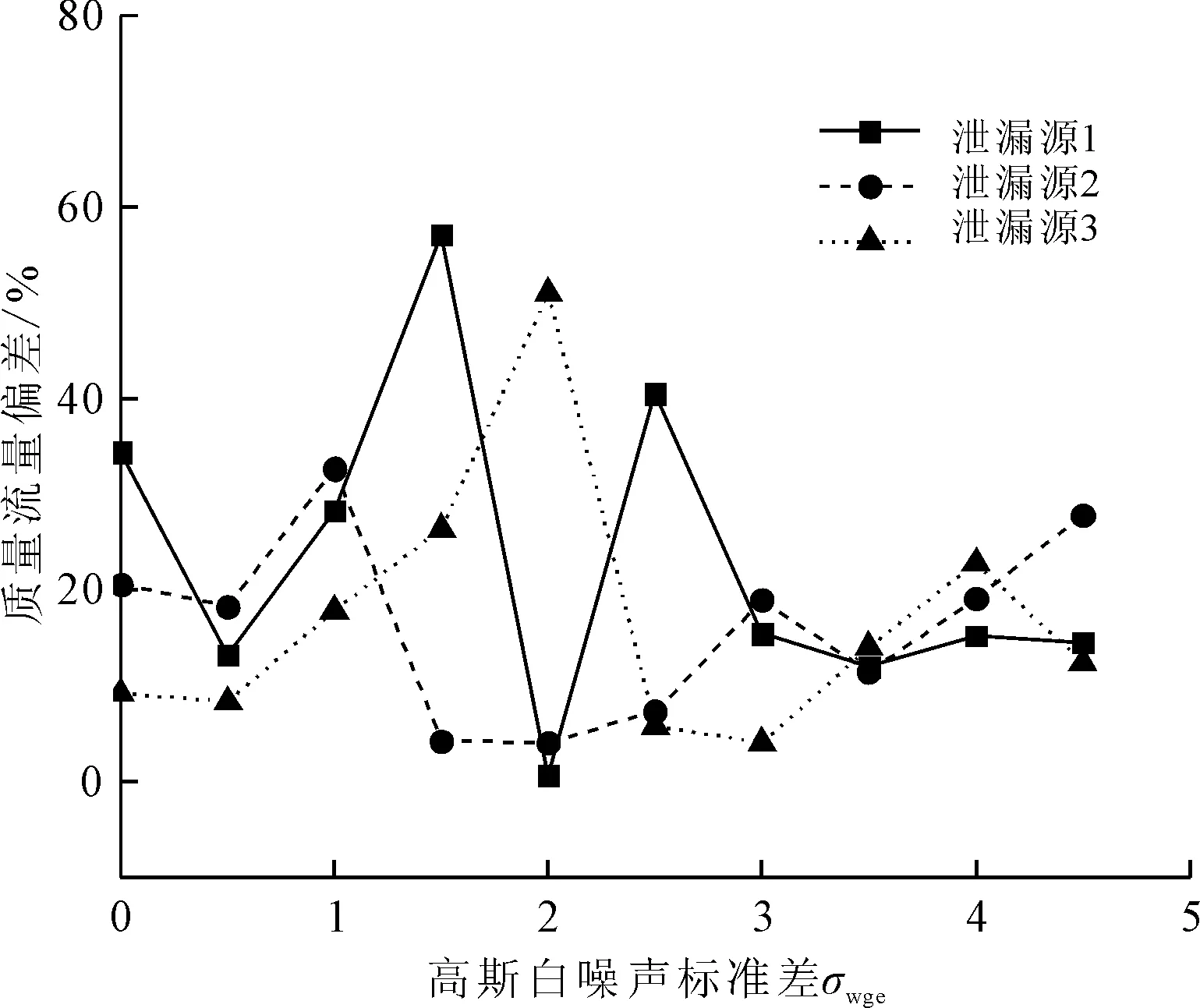
改进遗传算法(modified genetic algorithm，MGA)框架如图2所示。其中，S表示最优个体Pbest停止更新的代数，若最优个体在Smax代以内有更新，则令S=0；Hmax表示终止迭代的条件，若迭代次数超过Hmax，则停止计算并输出结果；α为交配率,用于调节正常交配和改进型交配(即与淘汰者基因交配或追随最优个体)的概率；β为母系遗传率；γ为追随率,表征某一个体靠近最优个体和在最优个体附近进行局部搜索的概率；θ为遗传算法的变异率。经过多次尝试，得到适用于多泄漏源场景定位的参数取值，如表1所示。令初始种群数量为100，最大迭代次数为500次，初始种群获取范围为图1所示的泄漏扩散场范围(0

图2 改进遗传算法框架

表1 改进遗传算法参数设置

若SSmax，则表示最优个体已经停止更新，需要加速算法收敛，这时需引导一部分个体(P1，P2)向最优个体Pbest靠拢(如式(4)所示)，再迫使一部分个体与最优个体交配(如式(5)所示)，从而实现最优个体附近的局部强化搜索。

(4)

(5)

式中：Pnew1和Pnew2为交配产生的新个体；Pbest为全局最优个体；Rf为[0,1]之间的随机数；P1和P2为随机选出的参与交配的个体；β为母系遗传率。

针对多源定位问题，需要重复进行多次MGA序列定位各个泄漏源。①假设泄漏场中只有一个泄漏源，对其进行MGA计算定位，从而找到一个潜在的泄漏源，并获得其泄漏扩散浓度场。②进行下一个泄漏源定位，假设上一个定位的泄漏源已经存在，并将其泄漏扩散浓度场的浓度分布加入正在求解的个体假想浓度场当中，再进行MGA计算定位。③每次求解一个新的泄漏源，都将前面所有已经定位出来的泄漏源浓度场加入到预测浓度场中，重复这一过程，直到所有的泄漏源均定位成功。序列MGA搜索多泄漏源的流程图如图3所示。

图3 序列MGA搜索多泄漏源的流程图

2 结果与讨论

2.1 MGA总体表现

为了测试MGA运算过程中最优个体的泄漏浓度预测偏差E随着迭代过程的变化规律，采用上述序列MGA方法对四源泄漏问题进行了测试。4个泄漏源的坐标分别为(260,-420)、(260,-40)、(260,240)、(312,128)，泄漏质量流量均为10 000 g/s，测量误差的标准差σwge设定为0.5，最终的定位结果如表2所示。其中，位置偏差为MGA预测各泄漏源位置与真实泄漏源的直线距离，泄漏质量流量偏差即为MGA预测各泄漏源的质量流量与真实泄漏源质量流量的差值绝对值在真实泄露源质量流量中所占的百分比。从表2可以看出，泄漏源预测的位置偏差均在1 m以内，泄漏质量流量的预测偏差均在40%以内，每个泄漏源定位的耗时在350～400 s之间。对于1 000 m×1 000 m的扩散范围，预测位置偏差在1 m以内可以认为定位成功。本次计算采用一台普通计算机运行，编程语言为Python，基本配置为Intel(R) Core(TM) i5-3450处理器搭载4.00 GB内存，算法并没有做并行运算处理。如果未来能够在工作站上进行并行运算，则可以减少计算时间。

针对上述四源问题，最优个体的预测偏差E的变化规律如图4所示，可以看出每次MGA计算的最优个体的E值均随种群迭代次数的增加而不断减小，直到定位成功一个泄漏源，这时E值基本保持不变。算法开始定位下一个泄漏源时，初始种群中最优个体给出的E值又重新经历迭代递减的过程。已定位的泄漏源越多，则定位成功时最优个体的E值就越小，到第4个泄漏源被定位成功后最优个体的E值与第3个泄漏源被定位时的E值已差别不大。之所以会有这样的变化规律，是因为采用了序列定位的策略。每次MGA只定位单个泄漏源，并将已经定位成功的泄漏源所产生的泄漏扩散浓度场加入正向模型(即式(1)中的浓度计算方程)的计算中。可见定位的泄漏源越多，则与所有泄漏源产生的真实浓度场越接近，所有传感器测量数据的对比偏差也就越小，这也导致了第1个泄漏源的质量流量和位置的预测偏差都最大。然而，由于前3个泄漏源定位均受到了其他泄漏源的干扰，泄漏质量流量和位置的预测偏差不断积累，这种影响随着多个泄漏源被定位成功逐渐体现在浓度值预测误差上，这也就导致了第3个和第4个泄漏源定位完成后最优个体的E值差别不大。总之，分析结果证明了序列MGA可以用于多个泄漏源的定位，且不会存在维度爆炸导致计算无法收敛的情况。

表2 序列MGA定位4个泄漏源的结果

图4 MGA最优个体泄漏浓度预测偏差E 的变化规律

为进一步测试MGA应对多个泄漏源场景的能力，采用MGA预测了1～5个泄漏源的场景，测量误差的标准差σwge均设为0.5，计算结果如表3所示。由表3可以看出，随着泄漏源数量的增加，单个泄漏源定位耗时略有增加，这主要是由于叠加更多泄漏源产生的浓度场造成的。针对不同的泄漏源数量，MGA预测的泄漏源位置偏差均小于1 m，泄漏质量流量偏差均在40%以内，再次证明了MGA定位多个泄漏源位置的能力。

表3 序列MGA定位不同数量泄漏源的结果

2.2 泄漏源相对位置的影响

一般而言，对于多源定位问题，比较难处理的情况包括：①多个泄漏源的扩散浓度场存在严重重叠，导致算法无法区别不同的泄漏源；②多个泄漏源沿风吹的方向分布、存在上下游关系时，泄漏源的扩散浓度场存在包含关系，算法无法准确判断泄漏源的扩散范围。针对这两种情况，笔者分别进行计算和分析。

(1)对于多个泄漏源产生的扩散浓度场存在重叠的情况，令两个泄漏源具有相同的x坐标，y轴方向距离不断缩小，即令扩散浓度场重叠的部分逐渐增加，用MGA预测二者的位置，测量误差的标准差σwge均设为0.5，结果如表4所示。由表4可以看出，随着两个泄漏源间的距离从100 m减小到2 m，MGA预测的位置偏差略有增加。当二者距离为2 m时，出现了大于1 m的位置预测偏差。但是，泄漏质量流量的预测偏差随二者距离的变化不显著，计算耗时随二者距离的减小也没有明显的变化规律。

为了更好地分析两个泄漏源扩散浓度场重叠所造成的影响，绘制MGA对不同y方向距离两个泄漏源预测位置偏差的平均值的变化情况，如图5所示。从图5可以看出，随着二者距离从100 m减小到2 m，两个泄漏源平均预测位置偏差逐渐增加。在小于20 m距离内，二者y方向距离的减小所导致的位置预测偏差增加得更加显著。图1显示单个泄漏源所产生的扩散浓度场大约覆盖了-50 m

(2)对于两个泄漏源处于相同的x方向，即二者沿着风吹的方向分布，存在上下游的关系，令两个泄漏源x方向距离从100 m增加到600 m，测量误差的标准差σwge均设为0.5，用MGA预测不同x方向距离下两个泄漏源的预测结果，如表5所示。从表5可以看出，处于风向上游的泄漏源预测位置偏差均小于1 m，而处于下游的泄漏源预测位置偏差较大，甚至有大于30 m的情况。这种偏差主要来源于对下游泄漏源x轴位置(即x0)预测的差别。处在风向上游的泄漏源(坐标(60,-40))的扩散浓度场覆盖范围明显会大于下游泄漏源，并将下游泄漏源的扩散场包含在内，因此MGA会有很大的概率先定位上游泄漏源且偏差较小。当MGA开始定位下游泄漏源时，由于其扩散浓度场的大部分信息被上游泄漏源干扰，有效信息较少，尤其是用于判断其x轴坐标位置的信息较少，因此MGA给出的x0预测偏差会比较大。可见，采用MGA预测两个存在上下游关系的泄漏源时，需要小心确定下游泄漏源的位置。

表4 两个具有相同x坐标的泄漏源不同y方向距离的MGA预测结果

图5 两个泄漏源y方向距离对MGA预测平均位置偏差的影响

表5 存在上下游关系的两个泄漏源不同x方向距离的MGA预测结果

2.3 测量误差的影响

在源强反算问题中，测量随机误差可能会对计算结果产生较大影响，因此有必要讨论MGA算法对于测量误差的适应能力。对3个坐标分别为(260,-420)、(260,-40)、(260,240)、泄漏质量流量均为10 000g/s的泄漏源进行MGA定位，在生成的测量数据中采用高斯白噪声分别加入不同大小的测量误差，预测的位置偏差和泄漏质量流量偏差分别如图6和图7所示。从图6可以看出，当测量误差的标准差小于1.5时，MGA对三源泄漏的位置预测表现较好。随着测量随机误差的增大，3个泄漏源的位置预测偏差也在不断增加。由于泄漏源1被第一个定位，泄漏场浓度包含了其他两个泄漏源浓度场的随机误差，因此其位置预测偏差最大。而泄漏源3被最后定位，由3个泄露源所预测的浓度场与真实浓度场之间的对比偏差已较小，故其位置预测偏差也较小。从图7可以看出，测量误差的变化对MGA预测多泄漏源质量流量的影响不显著。随着测量随机误差的增加，MGA对多泄漏源质量流量的预测偏差在60%以下随机波动，没有规律可循。在现场源强反算过程中，人们更加关注的是泄漏源位置的预判是否准确，因此MGA虽然在较大测量误差时无法非常准确地给出泄漏质量流量的判断，但还是可以指导现场泄漏源位置判断工作的。

图6 测量误差对三源MGA预测位置偏差的影响

图7 测量误差对三源MGA预测泄漏质量流量偏差的影响

3 结论

笔者提出了一种改进型的遗传算法(MGA)，用于开放扩散空间多个泄漏源的序列定位。对遗传算法的改进包括：给予被淘汰个体交配的机会，从而提高算法的全局搜索能力；在算法即将成熟阶段，引入部分个体追随最优个体的策略，加速算法收敛。针对采用高斯烟团模型获得的开放空间二维泄漏扩散浓度场进行了多个泄漏源的序列搜索，考察了泄漏源数目、泄漏源相对位置、测量随机误差的影响，并得到了以下结论：

(1)MGA可以实现1～5个泄漏源的定位，当测量随机误差的标准差为0.5时，预测位置偏差在1 m以内，泄漏质量流量偏差均在40%以内。

(2)当两个泄漏源的扩散浓度场发生重叠时，若二者垂直风向分布且距离在2 m以上，则MGA依然能够给出相对准确的定位。

(3)当两个泄漏源沿着风向分布导致二者的扩散浓度场存在包含关系时，MGA可以较准确地预测上游的泄漏源，但是对下游泄漏源的位置预测偏差较大。

(4)随着测量随机误差的增加，MGA对泄漏源位置的预测偏差逐渐增大，对泄漏质量流量的预测偏差变化不明显；当测量随机误差的标准差在1.5以下时，MGA的预测表现良好。