一类具比例时滞脉冲递归神经网络的全局多项式稳定性
周立群,宋协慧
(天津师范大学数学科学学院 天津 西青区 300387)
时滞递归神经网络(DRNNs)基于在联想记忆、优化控制、图像处理等领域的应用而被广泛研究。在这些应用中大多数都需要DRNNs 是稳定的,指数稳定性作为DRNNs 的一种重要的动力学性质[1-4],它的特征之一是Lyapunov 指数不等于0。然而大多数情况下,DRNNs 的最大Lyapunov 指数是等于零的,其状态轨迹渐近趋于平衡点,即此时DRNNs 是渐近稳定的[5-7]。
多项式稳定性是一种特殊的稳定性,它同指数稳定性一样蕴含着渐近稳定性,但其收敛速度比指数稳定性慢一些。它的特征之一就是其最大的Lyapunov 指数等于零。目前,这种系统的多项式稳定性研究较少,只有某些系统在某些特殊情况下才具有多项式稳定性,如波动方程[8-9]和随机微分方程[10-14]。需要说明的是,这里的多项式稳定性不是指对于一个多项式来研究这个多项式的稳定性,而是因为某些系统的解的估计式中含有t-λ(t≥t0, λ >0),类似于多项式,故称这种稳定性为多项式稳定性,具体见下文的定义。
由上所述,某种DRNNs 是否具有多项式稳定性?文献[15]回答了这个问题,文中给出了比例时滞递归神经网络(RNNs)多项式稳定性的定义,并研究了几类比例时滞RNNs 的多项式稳定性和多项式周期性。文献[16]将比例时滞引入细胞神经网络,提出比例时滞细胞神经网络模型。此后各种比例时滞RNNs 基于在二次规划问题和QoS 路由决策等方面的潜在应用得到了国内外学者的关注,并取得一些研究成果[17-26],但关于比例时滞RNNs的多项式稳定性的研究还很有限。
除了时滞效应外,脉冲也是影响神经网络动力学性质的重要因素之一。脉冲效应是指在网络运行过程中,系统的状态发生突变,导致网络的行为更加复杂,因此研究脉冲作用下系统的稳定性是非常必要的。目前,已有许多关于脉冲DRNNs 的动力学行为的研究成果[24,27-32]。文献[24]应用Lyapunov 稳定性理论结合线性矩阵不等式的方法研究一类比例时滞脉冲RNNs (IRNNs) 的无源性。然而,比例时滞IRNNs 的动力学行为的研究还很少。基于此,本文通过构造Lyapunov 泛函和LMI 的方法对一类比例时滞IRNNs的全局多项式稳定性进行探讨。
1 模型与预备知识



2 全局多项式稳定性









y=t-λ y=e-λt图1 函数 和 的图像
3 数值算例


且 λΞ= -12.756 7, -10.255 2, -7.726 6, -4.182 5,-2.375 5, -1.383 2, 即 Ξ <0。由定理1 可知,系统(19)是GPS。系统(19)的平衡点为x*=(0,0)T。时间响应轨线如图2~图5 所示。
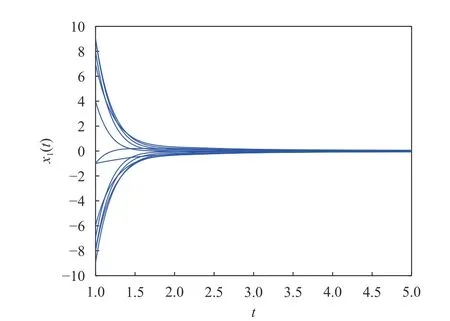
图2 系统(19)无脉冲时, x1(t)的时间响应轨线

图3 系统(19)带脉冲时, x1(t)的时间响应轨线

图4 系统(19)无脉冲时, x2(t)的时间响应轨线
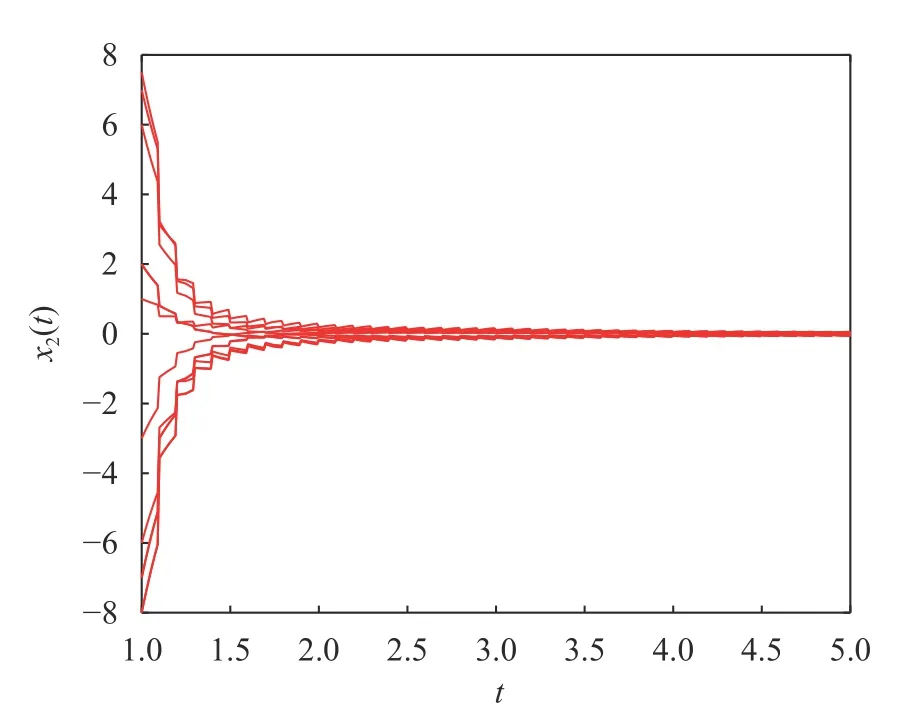
图5 系统(19)带脉冲时, x2(t)的时间响应轨线

得到矩阵 Ξ ,且 λΞ= -48.370 1, -21.586 4, -2.085 5,-5.302 1, -17.523 0, -8.011 9, -10.002 8, -14.865 7,-12.968 0, 由此可知Ξ <0,由定理1,可知系统(20)是GPS。由Matlab 计算,得系统(20)的平衡点为x*=(0.154 5, -0.539 5,1.880 5)T。时间响应曲线如图6~11 所示。
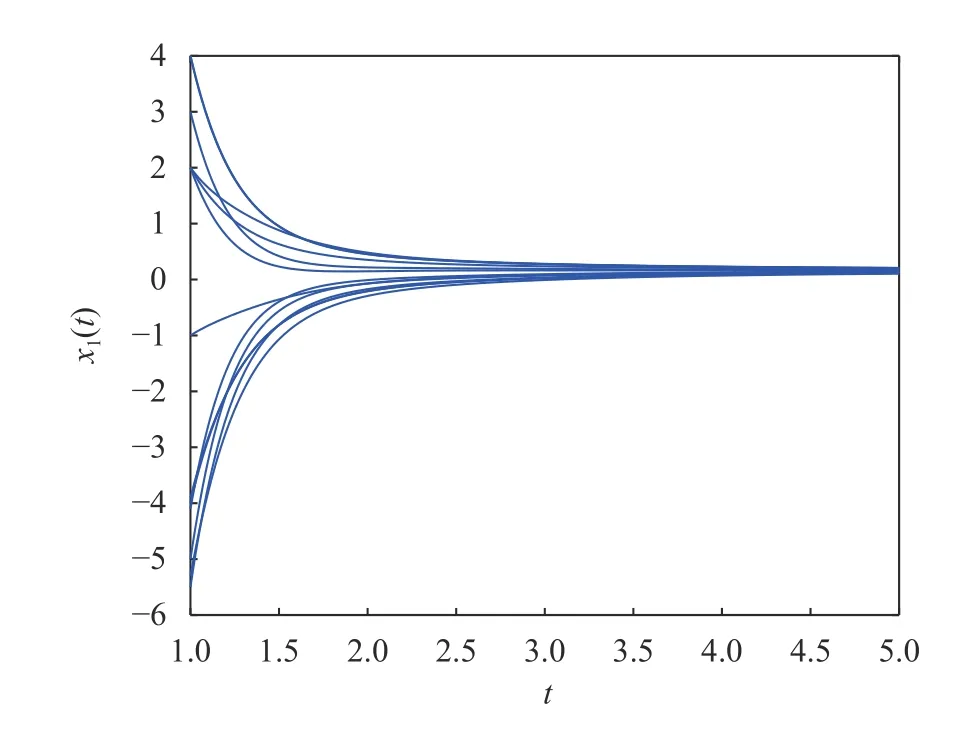
图6 系统(20)无脉冲时, x1(t)的时间响应轨线

图7 系统(20)带脉冲时, x1(t)的时间响应轨线
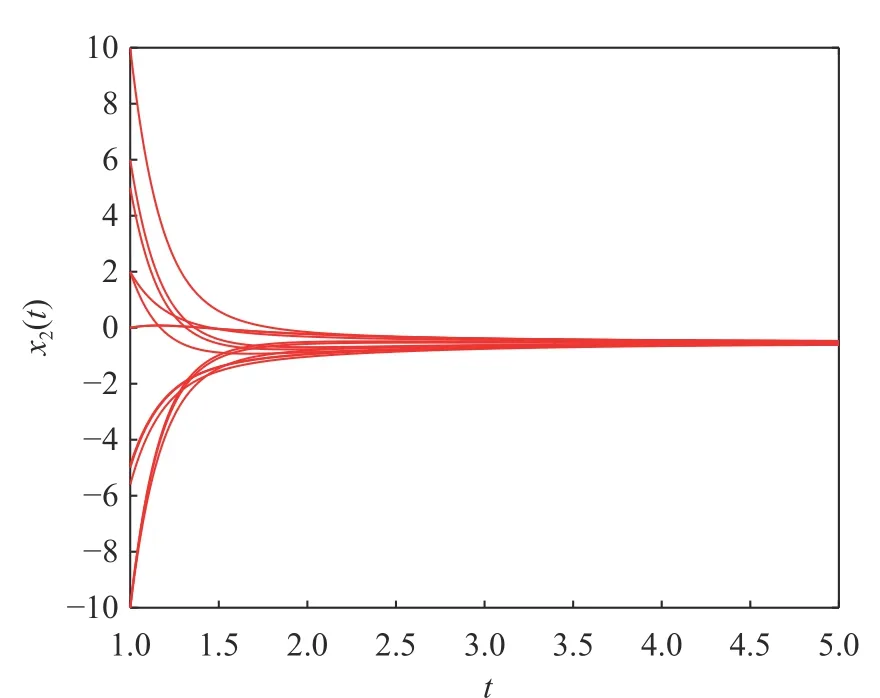
图8 系统(20)无脉冲时, x2(t)的时间响应轨线

图9 系统(20)带脉冲时, x2(t)的时间响应轨线
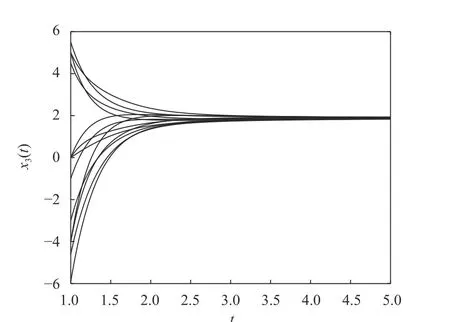
图10 系统(20)无脉冲时, x3(t)的时间响应轨线
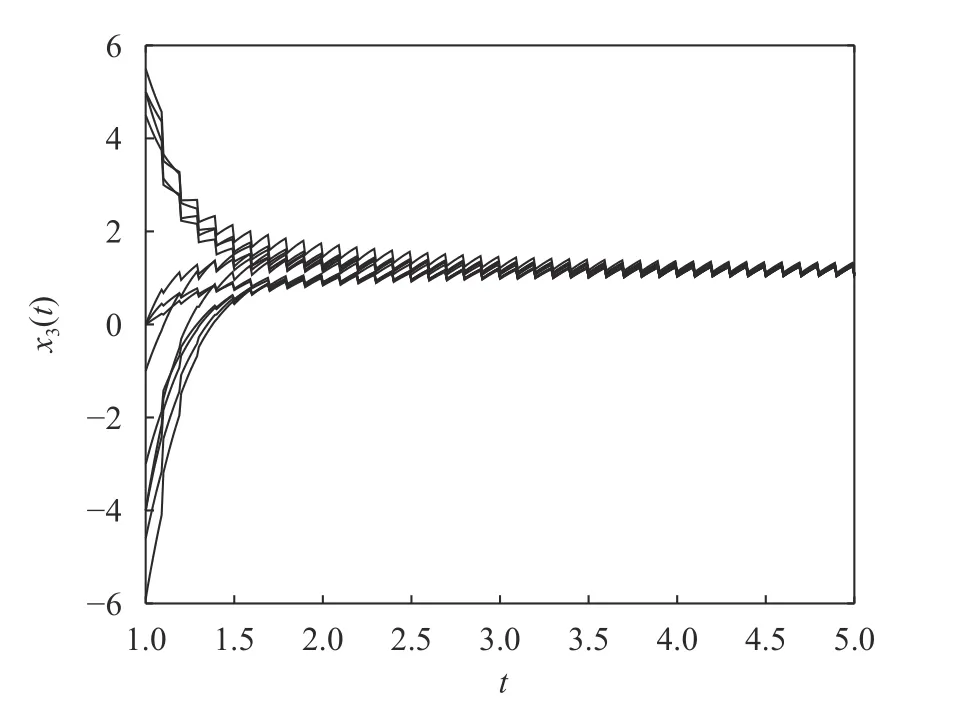
图11 系统(20)带脉冲时, x3(t)的时间响应轨线
4 结 束 语
本文通过构造合适的Lyapunov 泛函,研究了一类具比例时滞IRNNs 的全局多项式稳定性,所得准则是以LMI 形式给出的,便于应用Matlab 验证。可调参数的引入使得所得条件的适用范围扩大了。激活函数较广泛,可以是无界的,也可以是不可微的。本文的研究方法也适合于具比例时滞RNNs的多项式周期性、多项式同步性和多项式耗散性等动力学行为的研究。

