面向可穿戴生理信号的压缩感知实时重构

程云飞，叶娅兰*，侯孟书，何文文，李云霞

(1. 电子科技大学计算机科学与工程学院 成都 611731；2. 电子科技大学自动化工程学院 成都 611731)

近年来，人们对于自身健康越来越关注，基于可穿戴设备的远程健康监测得到了快速发展[1]。由于可穿戴设备对于功耗有着严格的要求，传统的奈奎斯特采样方法很难满足长期连续监测对于低功耗的需求，而压缩感知 (compressed sensing, CS)理论[2]很好地解决了这一问题。相较于奈奎斯特采样方法，压缩感知可以以较低的采样率对信号进行压缩采样，然后利用非线性的压缩感知重构算法从较少的采样值中重构出原始信号。通常，压缩感知假定信号在时域或某些变换域中是稀疏的，并利用信号的稀疏性来精确地重构信号。因此一些经典的针对稀疏信号的压缩感知重构算法被提出，如CoSaMP[3]、SL0[4]、BM-MAP-OMP[5]等。但是，有许多信号无论在时域还是在其他变换域中都是非稀疏的，如可穿戴远程健康监测系统中采集的生理信号[6]。因此，大多数压缩感知重构算法都不能很好地处理非稀疏生理信号。

为了解决非稀疏生理信号的压缩感知重构问题，文献[7]提出了一种块稀疏贝叶斯学习(block sparse bayesian learning, BSBL)框架以从压缩数据中恢复非稀疏信号，并基于边界最优化方法(bound optimization, BO)提出了BSBL-BO 算法，该算法可以以较高的精度直接从时域对非稀疏生理信号进行重构。然而该算法的时间复杂度较高，收敛速度慢，很难满足可穿戴远程健康监测系统对于实时性的要求。而文献[8]在BSBL 框架的基础上提出了BSBL-FM 算法，该算法虽然一定程度上提高了BSBL 算法的速度，但是其对于非稀疏信号的重构精度却无法保证。为了在不降低信号重构精度的前提下提高BSBL 算法的收敛速度，文献[9]基于交替向量乘子法(alternating direction method of multipliers,ADMM)对BSBL 算法的的迭代过程进行优化，提出了BSBL-ADMM 算法，在不降低重构精度的前提下大幅提高了BSBL 重构算法的收敛速度。尽管如此，所有传统压缩感知重构算法都是迭代式算法，这意味着这些算法必须经过多次迭代，直到收敛才能完成信号的重构。但在很多情况下，需要在一些计算能力受限的设备上(例如智能手机)进行实时数据处理，迭代式算法很难实时处理这些设备上接收到的压缩数据。

为了降低信号重构过程中的计算复杂度，文献[10]将深度学习中基于全连接层的堆叠去噪自编码器应用于生理信号的压缩感知重构。但随着信号长度的增加，网络参数的数量将急剧增加。这给模型的训练带来了很大的困难，并且还可能导致过度拟合。因此，这些基于全连接网络的方法通常在实验中会将生理信号划分为非常短的时间窗口 (远小于1 s)，而时间窗口太小可能会破坏信号结构的完整性并对后续的疾病诊断带来不利影响。

因此，本文基于深度学习中的一维扩张卷积[11]和残差网络[12]提出了一种面向可穿戴设备的生理信号压缩感知实时重构算法，扩张卷积可以大大减少模型参数数量，而残差网络则可以缓解模型训练期间的梯度衰减现象，从而提高网络模型的的性能。实验结果表明，在保证生理信号重构精度的前提下，本文所提方法的重构速度比传统的迭代式压缩感知重构算法快2～3 个数量级，从而更容易满足实际的可穿戴健康监护系统对于实时性的需求。

1 传统迭代式压缩感知重构

压缩感知是对信号边采样边压缩的一个过程，根据压缩感知的基本原理，其实际的采样过程是分时间窗对模拟信号进行随机的非等间隔采样，而这种随机非等间隔采样从数学的角度可以表示为预先生成的随机矩阵乘以一段高采样率的数字信号，即原始信号。因此压缩感知的采样过程可以表示为：

2 基于深度学习的生理信号重构算法

2.1 问题描述

在深度学习中，可以将压缩后的生理信号s与原始生理信号 α之间的关系看做是一个以s为输入，α为输出的非线性函数，根据通用近似定理[13]，深度神经网络可以通过学习在紧支撑集上逼近任意连续函数，这使得利用深度学习方法来实现压缩感知重构成为可能。

2.2 提出的网络模型结构

本文基于一维扩张卷积和残差网络设计了一个如图1 所示的面向可穿戴设备的压缩感知实时重构模型，简称为CS-DRN(compressed sensing-dilated residual network)。

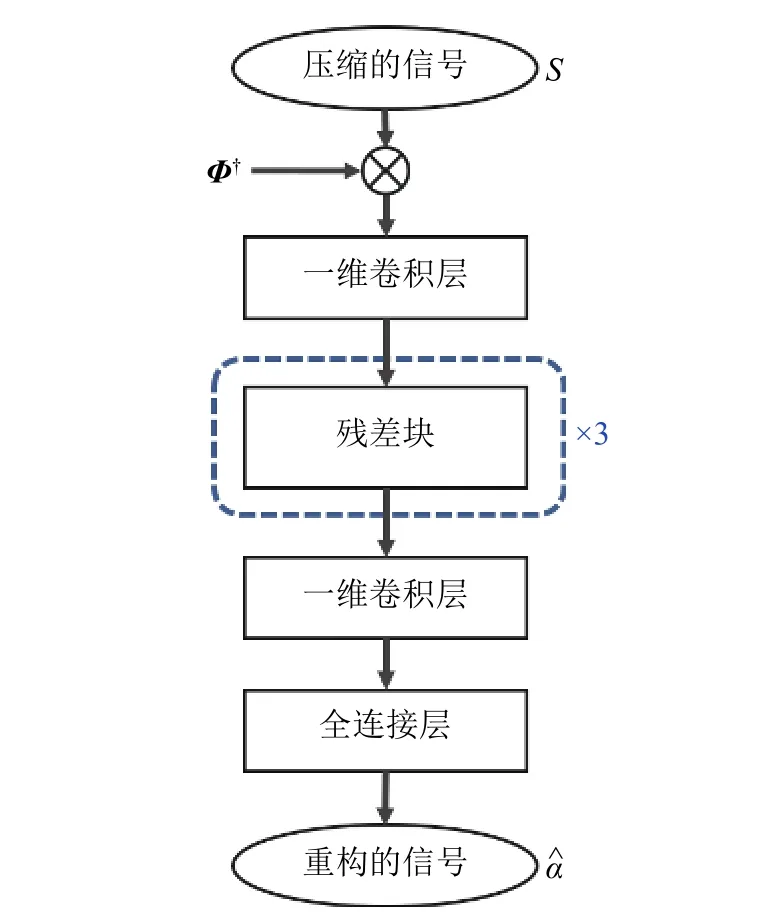
图1 本文提出的CS-DRN 模型整体结构

其中，所有卷积层均采用如类似图2 所示的一维扩展卷积。扩张卷积是传统卷积层的扩展，其为卷积层引入扩张率，扩张率定义了一个卷积核中的元素之间的间隔，扩张卷积通过在原始卷积核中插入间隔来扩大卷积核的感受野，同时确保卷积核中的参数数量不变。

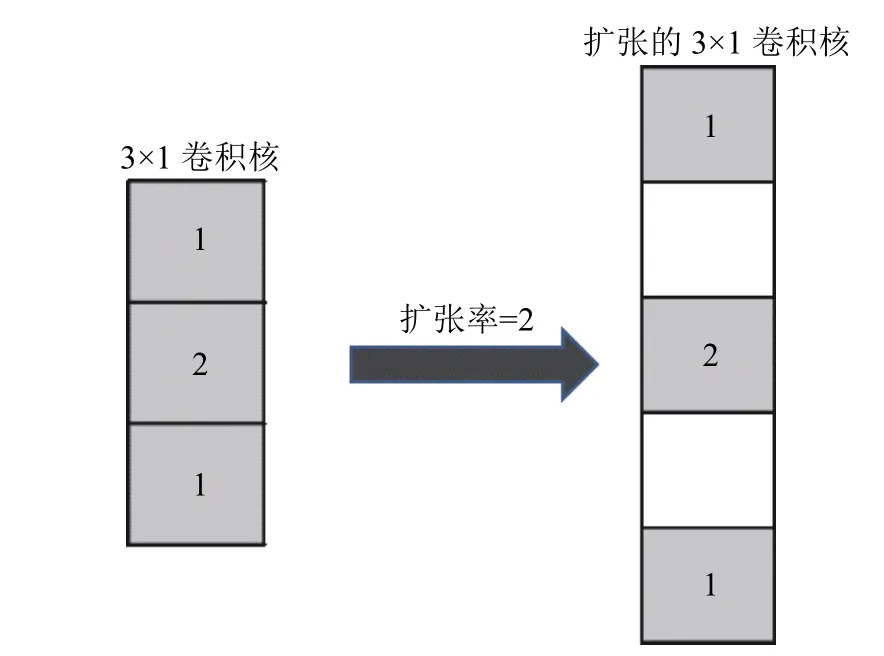
图2 本文所采用的一维扩张卷积

另外，为了解决一维生理信号的重构问题，提出了如图3 所示的3 层残差块单元。在残差网络中不仅将输入依次传递到下一层，并且还将输入叠加到到下一层的输出中。与传统的卷积神经网络相比，残差网络通过恒等快捷连接将数据流直接传递到后面的层，从而可以减轻由于多次堆叠的非线性变换而引起的梯度衰减。因此，残差网络可以构建更深的网络模型，并且训练也将更快。

图3 本文提出的残差块单元

本文提出的残差块单元包含3 个一维的扩张卷积层，在该残差块单元中，为了保证输入和输出可以直接相加，输入和输出的维度和尺寸必须保持一致，因此这里输入和输出均为16 个通道的特征图。残差块单元中3 个一维卷积层中的卷积核格式分别为32、64、16，对应的卷积核大小分别为7×1、5×1、3×1，并且所有卷积核的扩张率都设为2。为了保持特征图的尺寸保持不变，在每一层卷积中都根据当前卷积核的大小和扩张率设置合适的填充(Padding)值。在每一个卷积层后面都使用带泄露修正线性单元(Leaky ReLU)函数作为激活函数。

2.3 模型训练

在模型训练时，本文用Adam 优化器[14]对网络模型进行训练，学习率为0.001，训练过程中的批大小为128。模型基于python3.7.3 和pytorch 1.4.0深度学习框架进行实现。模型训练使用的计算机配备了英特尔i5-3 470 CPU、8 GB 内存和具有6 GB显存的英伟达GTX1060 显卡。

3 实验所用数据集以及评价指标

3.1 数据集

实验采用了两个公开的生理信号数据集，分别是OSET (open-source electrophysiological toolbox)[15]中的“signal01”数据集和mitdb (MIT-BIH arrhythmia database)[16]数据集。OSET 数据包括8 个采样率为1 000 Hz 的胎儿心电信号记录，而mitdb 数据集中则包含48 个长度为30 min 的两通道心电信号记录，采样率为360 Hz。两个数据集都被下采样到250 Hz，这也是在心电监测系统中最常用的采样率[17]。此外，从压缩感知原理来看，信号的采样与压缩应该是同时进行的。但是从算法研究的角度，需要原始的数字信号作为参照来评价算法的性能，因此基于压缩感知的数学模型，可以利用奈奎斯特采样的数字信号作为原始信号，通过数字方法对原始信号进行压缩，而不是直接从模拟信号进行压缩采样。

3.2 评价指标

PRD 越低代表着重构精度越高。

2) 为了评价信号重构算法的速度，本文将每个信号帧的重构时间作为反映算法速度的性能指标。为了便于比较几种算法的速度，除了深度网络模型训练时使用显卡计算外，生理信号的重构过程均只使用CPU 进行。

4 仿真实验

4.1 实验设置

由于压缩感知是对信号进行分段采集，因此本文的实验中，生理信号被分割为时间长度为2 s 的信号帧，在生理信号被分割后，随机选取其中80%作为训练集，剩余20%作为测试集。重构算法的对比都在测试集上进行。

由于生理信号被下采样到250 Hz，因此2 s 信号帧的长度为N=500。为了获得长度为M的压缩信号，需要先构建一个测量矩阵，本文使用稀疏二值矩阵[18]作为测量矩阵。在构造稀疏二值矩阵时，首先构造一个全零的矩阵，无论矩阵的行数是多少，在每一行中随机选择12 个元素，将其值置为1，从而生成稀疏二值矩阵。压缩率(compression ratio, CR)定义为：

4.2 算法对比

为了验证基于深度学习的非迭代方法在重构速度上的优势，本文将提出的CS-DRN 算法与BSBLADMM 算法、BSBL-FM 算法和BSBL-BO 算法的实验结果进行对比。此外，还对比了普通卷积神经网络 (CNN) 和堆叠去噪自编码器 (SDAE) 对生理信号重构的结果，从而证明本文提出的模型结构的有效性。对比实验中CS-CNN 模型采用了与CS-DRN基本相同的卷积层，但是未采用残差块结构，而SADE 的结构则参考文献[10]中提出的网络模型结构。由于可穿戴远程健康监测系统中采集的生理信号往往是非稀疏的[6]，因此在本文的所有实验中都是直接在时域对生理信号进行重构。以上算法中，迭代式压缩感知重构算法均基于Matlab 平台进行实现，而基于深度学习方法压缩感知重构算法都是利用python 语言和pytorch 框架实现。

表1 展示的是在OSET 数据集的测试集上重构误差的实验结果，从表中可以看出，BSBL-FM 算法的重构误差非常大，基本上无法对生理信号进行有效地重构。而BSBL-BO 算法的重构精度在大部分压缩率下都略优于BSBL-ADMM 算法，但在80%的压缩率下，BSBL-ADMM 算法的重构精度则略优于BSBL-BO 算法，而在90%的压缩率下，BSBL-BO算法的重构精度急剧降低，远差于BSBL-ADMM算法。相比之下，本文提出的CS-DRN 算法的重构精度在各种压缩率下均优于BSBL-ADMM 算法和BSBL-BO 算法。而对比CS-CNN 和SDAE 算法，CS-DRN 在各种压缩率下均优于这两种方法，这说明本文提出的深度网络模型结构相对更优。

表2 展示了6 种算法在不同压缩率下的平均重构时间，从表中可以看出，在同一压缩率下，BSBLADMM 算法的平均重构时间大约只有BSBL-BO算法的1/4 左右，而BSBL-FM 算法的平均重构时间介于前两者之间，并且这3 种算法的平均重构时间随着压缩率的增大而逐渐减小。而相比于这3 种迭代式压缩感知重构算法，另外3 种基于深度学习的非迭代压缩感知重构算法的平均重构时间要小2～3 个数量级，这是因为基于深度学习的方法在模型训练好以后，重构信号时只需要进行若干次矩阵向量乘法就可以完成对生理信号的重构。在这3 种非迭代压缩感知重构算法中，SDAE 算法的平均重构时间是随着压缩率的增大而逐渐减小，这是因为SDAE 算法的模型结构是基于全连接网络的，模型参数数量会随着输入信号长度的增加而呈指数级增加。而本文提出的CS-DRN 算法以及CS-CNN算法的平均重构时间并不会随压缩率的变化而产生较大差异，这是由于卷积层基于参数共享机制，通过卷积核的平移来提取特征，卷积核的参数数量并不会因为输入长度的不同而发生变化。因此当划分信号帧的长度大幅增加时，CS-DRN 算法和CSCNN 算法的平均重构时间不会急剧增加。另外，从表2 中看到，对于一个2 s 的信号帧，对比的几种算法在各种压缩率下的重构时间基本都在1 s 以内，似乎都满足了实时性需求。然而具体的算法重构时间是依赖于计算机硬件性能的。对于计算性能充足的高性能计算机来说，这些算法的实时性都没有问题，但是针对可穿戴健康生理信号监测场景来说，信号重构的过程很有可能需要在计算能力受限的便携式设备 (如智能手机) 上进行，此时迭代式压缩感知算法就很难满足实时性需求。因此需要尽量降低重构算法的复杂度，减少重构所需时间。

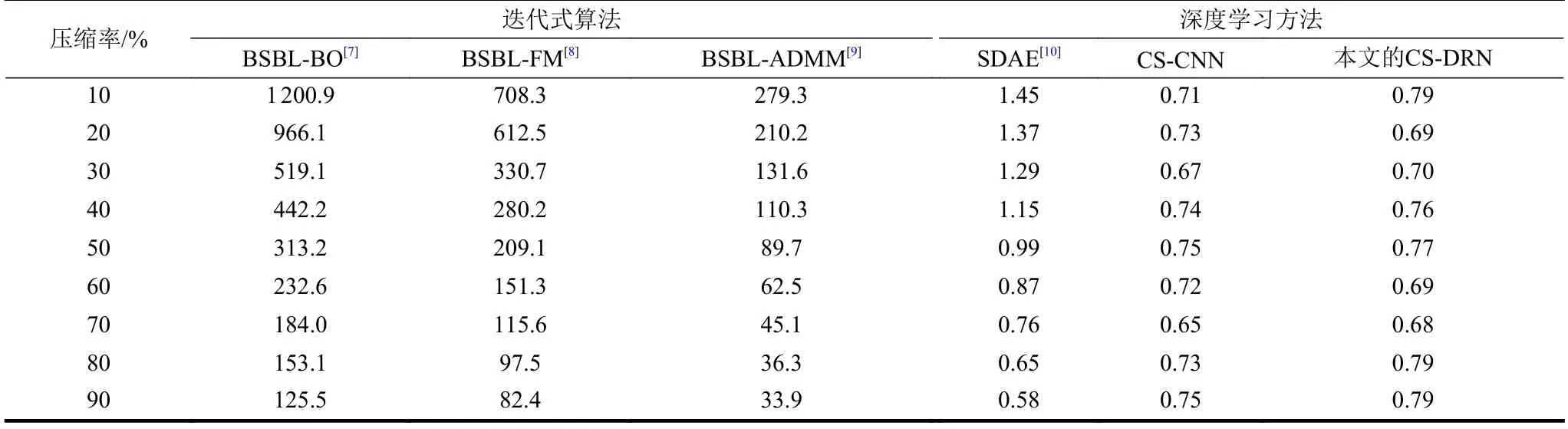
表2 OSET 数据集上6 种算法在不同压缩率下的平均重构时间 ms

为了更好地验证本文提出的CS-DRN 算法的性能，除了OSET 数据集以外，本文还在mitdb 数据集上进行了生理信号重构的实验。图4 展示了在mitdb 数据集上6 种压缩感知重构算法在不同压缩率下重构误差的对比情况。由图中可以看出，各种算法的重构误差都随着压缩率的增加而增大，其中BSBL-FM 算法的重构误差在各种压缩率下均远大于其他几种算法。除了BSBL-BO 算法在高压缩率下重构误差急剧增加外，其他几种算法的重构误差都比较接近。本文提出的CS-DRN 算法在不同压缩率下的重构精度都要优于另外几种算法。这与在OSET 数据集上的得到的结论一致。

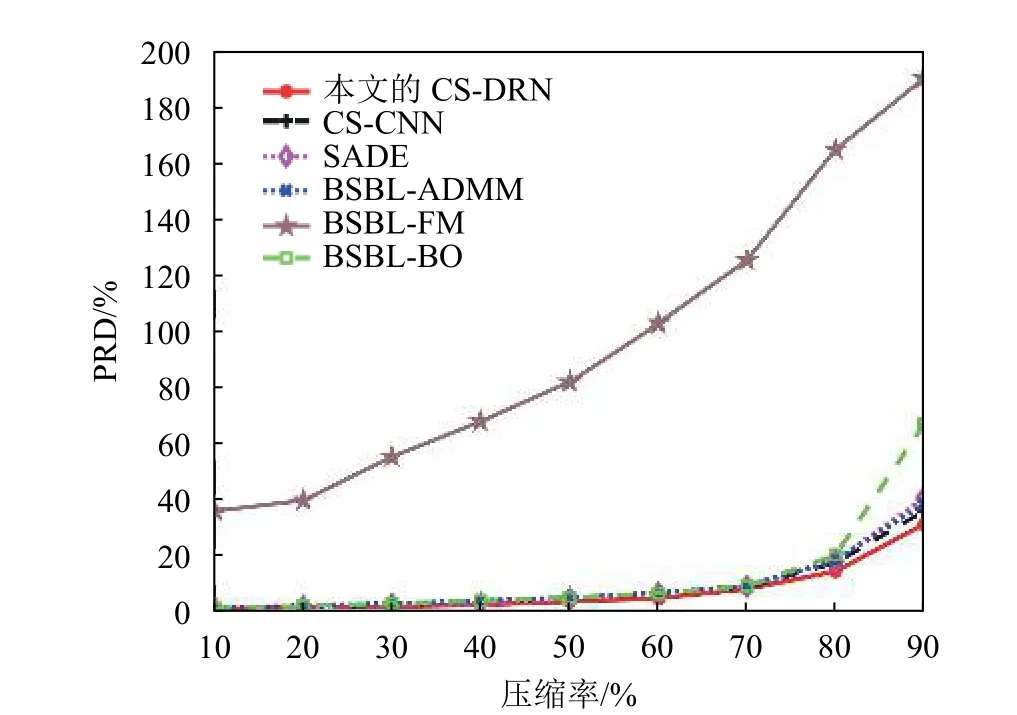
图4 6 种算法在不同压缩率下的PRD

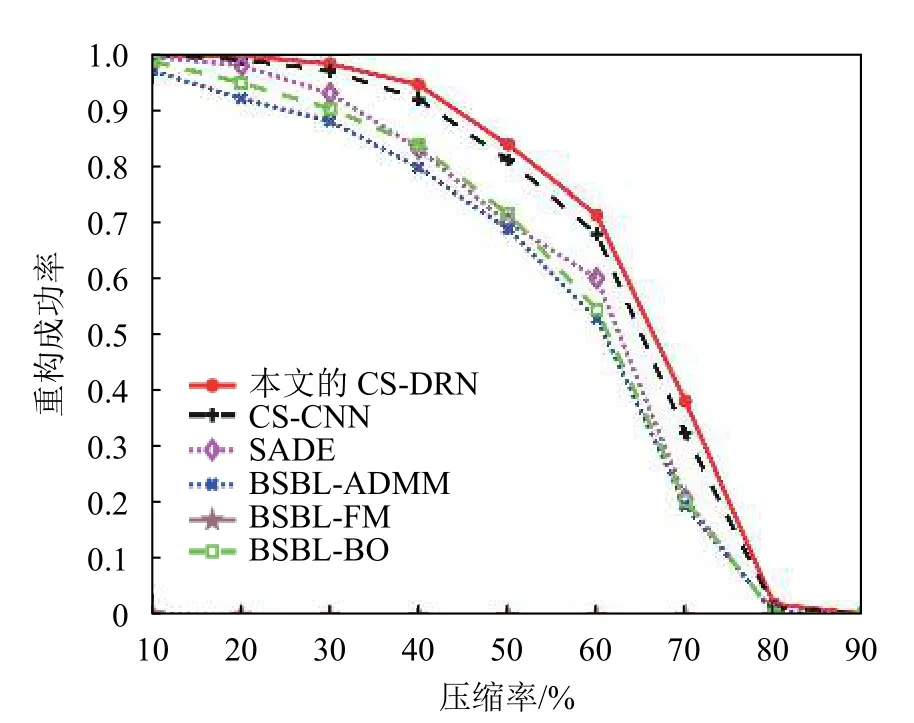
图5 6 种算法在不同压缩率下的重构成功率

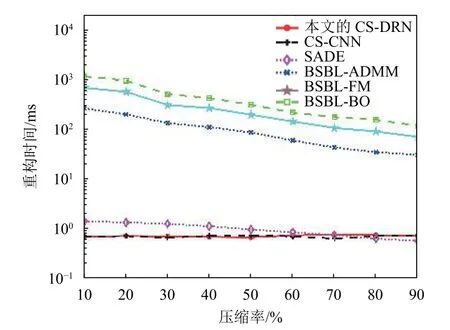
图6 6 种算法在不同压缩率下的平均重构时间

此外，本文定义了一个阈值 ε=5%，当一个信号帧的PRD 低于或等于这个阈值时，则认为该信号帧重构成功。本文将测试集中所有信号帧统计重构成功率作为算法重构性能的一个评价指标，重构成功率越高则代表算法的重构性能越好。图5 给出了6 种算法在mitdb 数据集上重构成功率的对比，从图中可以看到，除BSBL-FM 算法在各种压缩率下均无法有效重构生理信号外，其他几种算法的重构成功率均随压缩率的增大而减小，而本文提出的CS-DRN 算法则在各种压缩率下的重构成功率都优于另外几种算法，这说明CS-DRN 算法的重构性能在这几种算法中是最优的。

图6 给出了在mitdb 数据集上6 种算法的平均重构时间，为了便于展示，图中纵坐标轴的刻度以对数表示。从图中可以看到，BSBL-ADMM、BSBLFM 和BSBL-BO 这3 种算法的平均重构时间要比其他3 种非迭代式压缩感知重构算法大2～3 个数量级。在3 种基于深度学习的非迭代压缩感知重构算法中，SDAE 算法的平均重构时间是随着压缩率的增大而减小的，而本文提出的CS-DRN 算法以及CS-CNN 算法的平均重构时间则不会随压缩率的变化产生较大的差异。这也与OSET 数据集上得到的结论一致。

4.3 实验结论

综上所述，本文实验分别在OSET 数据集和mitdb 数据集上进行了压缩感知重构实验，并与另外两种基于深度学习的非迭代压缩感知重构算法和两种迭代式压缩感知重构算法在重构精度和重构速度上进行了比较。实验结果表明，对于生理信号的压缩感知重构问题，本文提出的CS-DRN 算法所需的平均重构时间要比BSBL-ADMM、BSBL-FM和BSBL-BO 这3 种迭代式的压缩感知重构算法小2～3 个数量级，并且CS-DRN 算法的重构精度在各种压缩率下均优于其他几种压缩感知重构算法。

5 结 束 语

本文提出了一种基于深度学习的非迭代方法来进行生理信号的压缩感知重构。相比于传统的迭代式压缩感知重构算法，本文所提出的方法在生理信号重构阶段无需进行迭代，在有着更高重构精度的前提下，其重构速度要比传统的迭代式压缩感知重构算法快2～3 个数量级，更容易满足实时性需求。因此，本方法在可穿戴远程健康监测系统中具有良好的应用前景。