基于环形抽样代理模型的结构可靠性分析方法

周成宁，肖宁聪*，李兴国，张 军

(1. 电子科技大学机械与电气工程学院 成都 611731；2. 成都步科智能有限公司 成都 611730；3. 西安航天动力测控技术研究所 西安 710038)

工程中的不确定性广泛存在，如振动、冲击、加速度、噪声及载荷等，这些因素对结构的性能和可靠性产生重要影响[1]。结构可靠性理论和方法为处理工程中各种不确定性问题提供有效解决途径。

蒙特卡洛仿真(monte carlo simulation, MCS)方法具有较高的精度和鲁棒性，其可靠性分析结果常常作为衡量其他方法优劣的标准，广泛应用于结构可靠性分析领域[2]。但对于小概率问题，MCS 方法需要大量样本来保证精度，尤其性能函数是隐式时，需通过数值仿真，如有限元分析(finite element analysis, FEA)[3-4]求解输入变量的输出响应，导致可靠性分析耗费大量时间，效率低下。为了提高可靠性分析的效率，一阶、二阶可靠性分析方法(first-/second-order reliability methods, FORM/SORM)[5]被广泛采用。FORM、SORM 在可靠性设计点(most probable point, MPP)对性能函数分别进行一阶、二阶泰勒展开。然而，由于忽略展开式中的高阶项，对于非线性程度较高的性能函数，FORM、SORM 的精度较低，很难得到准确的可靠性指标。为了更好地平衡精度和效率，近年来，代理模型技术在结构可靠性领域广泛发展。常见的代理模型有：响应面法(response surface method,RSM)[6-7]、神经网络(neural networks, NN)[8-9]、支持向量机(support vector machine, SVM)[10-11]、克里金插值(Kriging)[12-18]等。

Kriging 模型因具有准确的插值特性和提供估计值的不确定性方差，而被广泛应用于结构可靠性领域。文献[19]提出一种学习方程— U 方程，为Kriging 在结构可靠性领域广泛发展奠定了坚实的基础；文献[17]提出一种基于子集模拟(subset simulation, SS)的可靠性分析方法，为解决小概率失效问题提供了一种可行的途径；文献[18]考虑变量权重并保证所选样本点之间保持一定的距离且分布在极限状态方程周围；文献[20]引入了K-Means 聚类算法考虑变量之间的相关性问题；文献[21]连接极限状态方程两侧异号的特定样本点，再在此直线上随机产生n个样本点，寻找最佳候选样本点。虽然以上方法都在一定程度上提升了可靠性分析的效率，但很少关注代理模型更新过程中的抽样区域问题；鉴于此，本文通过 3σ准则、欧式距离确定代理模型更新过程中的抽样区域，避免因对失效概率贡献较小的区域持续抽样而造成计算资源的浪费，提高了可靠性分析的效率。另外，通过改变抽样区域带宽，该方法也可用于解决结构可靠性分析中的小失效概率问题。

1 Kriging 模型

Kriging 模型(高斯过程回归)是起源于地质统计学的一种插值方法，不仅可以估计样本点响应的均值，还可以表征估计结果不确定程度，目前在可靠性领域已得到广泛的应用。Kriging 模型通常分为线性回归部分和随机过程部分，其数学模型可表示为[22]：

2 代理模型更新与抽样策略

构建高效的代理模型，样本点的选取策略是关键。设计空间不同区域的样本点对失效概率的贡献不一样，因此在代理模型构建过程中，若在贡献较小的区域过多的选取样本点，或贡献较大的区域过少的选取样本点，都会影响代理模型的构建效率和精度；再者，依据传统的AK-MCS 方法选取样本点，同样避免不了对失效概率贡献较小的区域过多的选取样本点。基于代理模型的结构可靠性分析中，为了提高所构建模型的建模效率和精度，需构建特定的抽样区域，该区域的样本点相对其他区域样本点对失效概率有较大的贡献。因此，所选样本点应分布在极限状态方程附近；再构建抽样特定区域，通过选取该区域内的样本点对代理模型进行更新。分析如下。

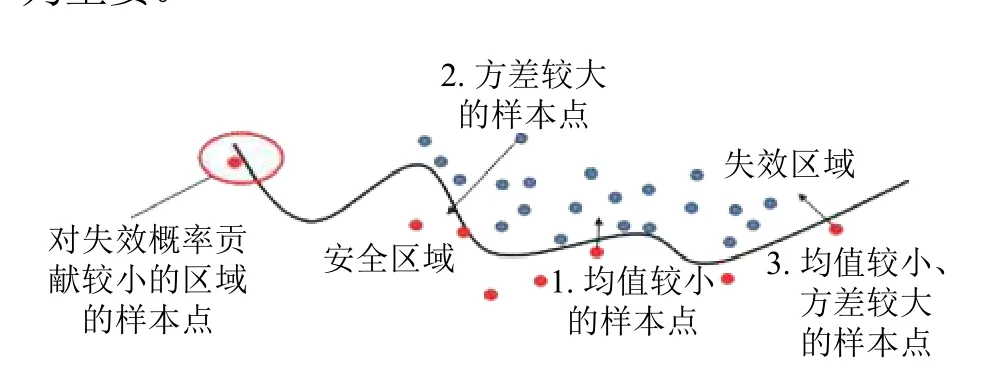
图1 U 方程选取的3 类样本点

2)蒙特卡洛抽样的样本分布情况如图2 所示(如变量服从高斯分布)，对于结构可靠性分析中的小概率失效问题，设计空间的最优样本点往往存在于蒙特卡洛抽样样本分布的边缘部分，如图3 中红色虚线之间的蓝色样本点；假设有1×106个样本服从标准正态分布，且失效概率的数量级为10-3，由3σ准则可得，分布在各个区间的样本量数目如图4所示，并且随着区间远离原点，区间内的样本数量急剧减少。如图4 所示，即使区间 [4,+∞)内的31.67 个样本全部落在失效域内，对失效概率的贡献仅仅为10-5数量级；况且，对于结构可靠性中小概率失效问题，区间[ 4,+∞)内的样本仅有少量分布于可靠性问题的失效区域。因此，此区域的样本点最终对失效概率的贡献估计仅为10-6数量级，甚至更小，可忽略不计。另外，如图3 所示，外圈红色虚线外侧的样本点对模型更新后的准确率影响较小；同理，内圈红色虚线内侧的样本点对模型更新后的准确率影响同样较小。因此，为了避免代理模型更新过程中对失效概率贡献较小的区域过多抽样或对失效概率贡献较大的区域过少抽样，图3 红色虚线区域样本点即为最佳样本点的目标区域(样本服从标准正态分布)。

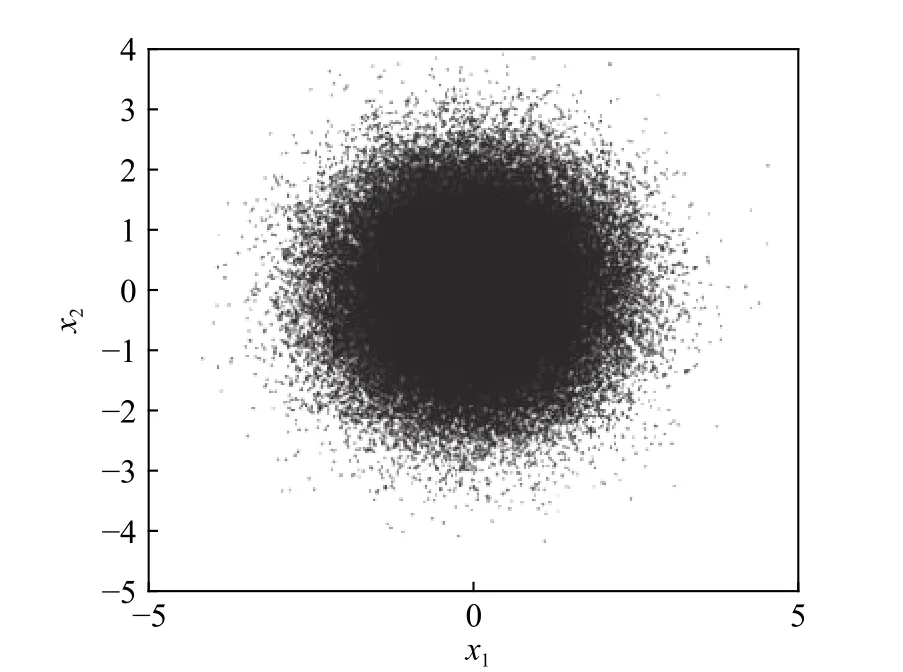
图2 蒙特卡洛产生的候选样本点

图3 所提方法抽样策略的抽样区域

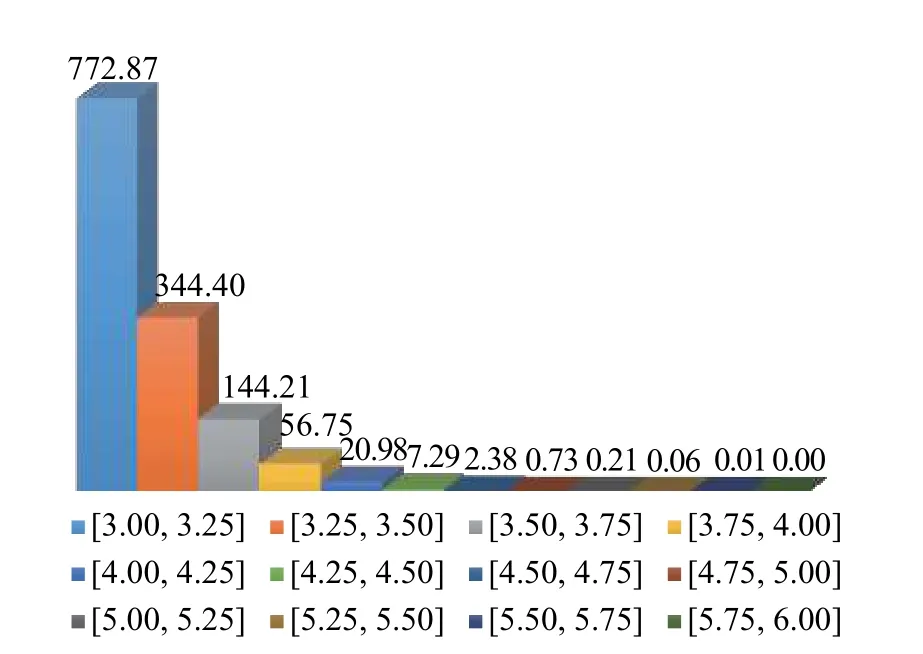
图4 标准正态分布各区间内样本点数量

通过以上优化方法在目标区域选取最佳样本点，代理模型不断迭代更新，直至满足收敛条件，见参考文献[19]。最终求得失效概率，完整的可靠性分析步骤如下。

1) 通过MCS 产生N个样本点，本文随机选择12 个样本点，作为设计空间(design of experiment,DoE)的初始样本点;

2) 更新DoE 中的样本点，通过DoE 中的样本点构建更新Kriging 模型，用此模型预测步骤1) 中N个样本点的均值和方差；

3) 通过欧氏距离确定环形抽样区域Z；

3 算例分析

表1 几种方法的精度与效率对比

为了说明建模过程中样本点的选取、收敛情况，选取了其中一次计算结果。图5、图6 分别为本文方法在构建代理模型过程中迭代抽样示意图，以及样本量与失效概率的关系变化情况。从图5 中可以看出，本文方法在更新代理模型的过程中避开了对失效概率贡献较小的区域抽样，从而实现抽样集中在对失效概率贡献大的区域。代理模型与极限状态方程能较好的拟合。

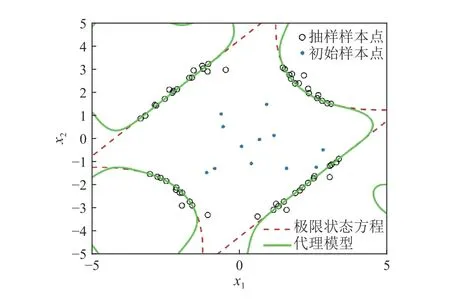
图5 本文方法抽样示意图

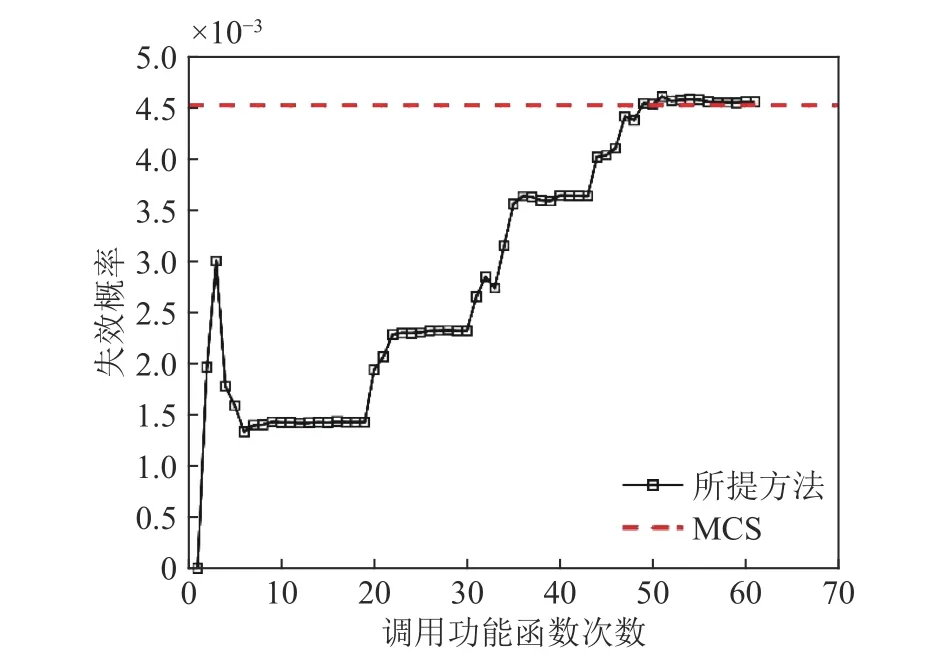
图6 本文方法样本量与对应的失效概率

图7、图8 分别给出了经典AK-MCS方法在构建代理模型过程中迭代抽样示意图，以及样本量与失效概率的关系变化情况。从图5、图7中不难发现，在选取相同初始点的情况下，图5 抽样的样本点数量明显少于图7，效率提升明显。另外，从图6、图8 可知，本文方法与AK-MCS 方法均能得到精度较高的结果，但调用性能函数的次数明显少于AK-MCS 方法。

图7 AK-MCS 抽样示意图

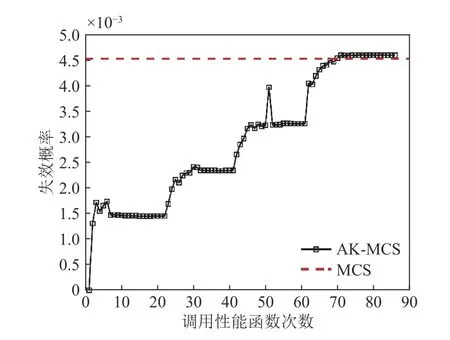
图8 AK-MCS 样本量与对应的失效概率

4 结 束 语

本文基于欧氏距离环形抽样，对基于Kriging 代理模型的结构可靠性分析方法进行了研究，并用数值算例验证了该方法的合理性，结果如下：

1) 工程中涉及到的性能函数往往是隐式的，需要通过FEA 计算响应值。然而，FEA 非常耗时，因此，基于代理模型的高效结构可靠性分析方法可提升可靠性分析的效率；

2) 本文方法中的环形抽样区域通过欧氏距离进行确定，使代理模型在更新过程中避免了对失效概率贡献小的区域进行重复抽样，提升了可靠性分析的效率；

3) 本文方法具有较高的精度和效率，可应用于结构可靠性及可靠性灵敏度分析。同时，可通过改变环形抽样区域的大小来提升方法的鲁棒性和计算效率。