A fitting formula for electron–ion energy partition fraction of 3.54-MeV fusion alpha particles in hot dense deuterium–tritium plasmas*

Yan-Ning Zhang(张艳宁), Zhi-Gang Wang(王志刚), Yong-Tao Zhao(赵永涛), and Bin He(何斌),†

1School of Science,Xi’an Jiaotong University,Xi’an 710049,China

2Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

Keywords: inertial confinement fusion,deuterium–tritium plasma,alpha heating,energy loss

1. Introduction

Heating of deuterium (D) and tritium (T) ions by 3.54-MeV alpha particles in plasmas is a basic problem in controlled fusion, which is called as alpha heating. The relevant investigation has been made over half a century.[1,2]An important parameter to describe the heating is the electron–ion energy partition fraction η, defined as the ratio of the energy obtained by both D and T ions to 3.54-MeV projectile energy.In order to simulate the pellet gain and the burn processes in inertial confinement fusion (ICF),[3]the values of the partition fraction should be known for wide ranges of the electron(Te) and ion (Ti) temperatures from tens of eV to 200.0 keV,and electron number density (ne) from ～1021cm-3to ～1026cm-3.[4,5]

As the energy partition fraction is important for the simulation of alpha heating in DT plasmas,some fitting formulas have been given at some plasma densities when Te=Ti. As far as we know, the earliest formula was presented by Fraley et al.,[6]by means of the binary collision (BC) theory.[7]They found η = Te/(Te+32) (Teis measured in unit keV)when ρ =0.213 g/cc, and η =0.5 when ρ =104g/cc and Te=24 keV.Later by the same BC model,Atzeni and Meyerter-Vehn(AM)[8]gave η =Te/(Te+25)(Teis in unit of keV)when ρ =10.0 g/cc–100.0 g/cc for typical ICF fuel density.However, they all ignored the important cases when Te／=Ti,which usually happen in the heating process. Thus it is necessary to carry out a fitting formula as a function of ρ, Te, and Tifor convenient application in related simulation. This is the main motivation of the present work.

So far there are several models to calculate η from different physical pictures, including the classical binary collision model,[7]the collective effect or plasma polarization model[9]by means of the classical dielectric function,[10]Li and Petrasso (LP) model[11]which combined the binary collision and collective effect, and the model[12]proposed by Brown,Preston, and Singleton Jr (BPS) on the basis of a simplified Fokker–Plank equation.[13]In recent time we suggested a model[14]that was able to bring reliable values of η in wide ranges of the plasma densities and temperatures.In the present work the fitting formula is given according to the data by our model.

Totally speaking,previous research about the energy fraction partition was obtained in the non-relativistic framework and the possible relativistic effect was not investigated but it might appear when Tebecomes very high such as 100 keV–200 keV. Therefore, it is necessary to check whether the relativistic motion of the electrons in the plasmas affects the energy partition fraction. This is the second purpose of the present work.For this goal,the relativistic model suggested by Prentice[15]is revised to gain more reasonable result of stopping power.

This paper is organized as follows. In Section 2, a brief description about our model is presented, followed by some typical features of the energy partition fraction. In Section 3, an investigation of relativistic motion of electrons for Te≥50.0 keV is made for the possible influence upon η. In the last section, a fitting formula is given together with the fitting error. Comparisons with other works are made in this section, and the difference is explained. Finally, some conclusions are drawn. In the following the word plasma means the dense ICF DT plasma. In the current work, the plasma mass density varies from 1.0 g/cc to 10.03g/cc, and temperature changes from 100 eV to 100 keV. The projectile is always alpha particle, and the maximum of kinetic energy E is 3.54 MeV.Deuteron and triton in the plasmas are called as DT ion for simplicity. The atomic units(e=me=ħ=1)are used in this work unless otherwise explicitly indicated.

2. Brief introduction of our model and some features of η

Although some models have been suggested to estimate the energy partition fraction, further revisions are still necessary to get more reliable data for relevant research. In the BC model the projectile slows down due to the Coulomb collision with the charged particles in the plasmas. Here the Coulomb logarithm logΛ related to Debye length λDis used,but it is invalid at high plasma density and low temperature. Moreover,the results from this model depend on the choice of Coulomb logarithm. In the picture of collective effect,the projectile polarizes the plasma and an electro-static field is excited. Therewith the projectile feels a retarding force that retards its motion. However,the projectile is usually assumed to move in a straight line so that the energy loss always happens even the projectile energy Epis far below the plasma temperature. Obviously it is unreasonable since the projectile must be thermalized at the ambient plasma temperature. In LP model the collective effect was represented by a logarithmic term,which is valid only when the projectile velocity Vpis much larger than the thermal velocity of the electrons or ions in the plasmas, as pointed in Ref. [10]. However, the collective effect at a lower Vpis also necessary for the accurate estimation of the energy transferred to the plasmas. In BPS model, the basic dimensionless parameter g (=1/(λDTe)) should be much smaller than 1. This is not satisfied in the case of high plasma density and low temperature. For example, g is higher than 0.34 when Teis around 0.1 keV while neis around 1026cm-3.

In order to better explore the slowing down of alpha particles in ICF dense DT plasmas, the mechanism of the plasma polarization described by the quantum dielectric function ε(k,ω) and the effect of the projectile recoil[16–18]were combined in our previous work.[12]Here the rate of projectile energy change due to plasma electron or ion is obtained as

Fig.1. Ionic component of stopping power SPi in DT plasmas as a function of Ep at different Ti when ρ =4.15 g/cc and Te =5.0 keV. The line with empty circles denotes SPe.

Figure 2 shows the SPiand SPein DT plasmas as a function of Epat different Tiwhen ρ=4.15 g/cc and Te=5.0 keV.Here SPeis almost independent of Tisince the mass of electron is much smaller than that of DT ions.This figure indicates that the SPiat different Tiis close to each other for Ep=10 keV/u.This is also valid when Epis higher. This is the asymptotic behavior of stopping power[19]since the corresponding Vpis much higher than the thermal velocity of the DT ions. Hence,for Epbetween 10 keV/u and 885 keV/u the corresponding τ(Ep)is irrelevant with Ti. Moreover, τ(Ep)in this Eprange contributes more than 90% of the energy partition fractions.These make η in this case weak dependence upon Ti. Therefore,the asymptotic behavior of SPiand weak dependence of SPeupon Tilead to the last feature of η.

3. The η in relativistic plasmas

As the plasma temperature may be quite high, such as Te=100 keV, the relativistic effect of electrons in the plasmas should be considered although the effect for ions is still very weak. The reason is that the ion is much heavier than the electron so that the ion thermal velocity is much smaller than the light speed c. More than 50 years ago,Prentice[15]derived some analytical expressions for stopping power of ions in very hot plasmas,where relativistic effect was completely included on the base of classical dielectric function. However, in that work the projectile was assumed to move in a straight line in the plasmas, which made it still lose energy even if its Epis much smaller than the plasma Te. This is not suitable according to the description in the last section. For this reason the projectile recoil is introduced in the same way as Eq. (5) in Ref.[20],and the energy loss rate comes to be

Fig. 2. SPe in DT plasmas as a function of Ep by different models at Ti =Te =100 keV and ne =1026/cc. The line with squares and circles denote the result considering the recoil of the projectile with non-relativistic and relativistic momentum distribution of the electrons, respectively. The line with up and down triangles denote the result without the recoil of the projectile when non-relativistic and relativistic momentum distribution of the electrons are considered,respectively.

The above figure indicates clearly that the results with the recoil of the projectile is quite different from that without the recoil. Meanwhile the result by relativistic momentum distribution is close to that by non-relativistic distribution when Ep＜1.0 MeV,which covers most range for SPito play its role to affect η. With Epincreasing,SPeby relativistic momentum distribution becomes a few higher than that by non-relativistic distribution. The reason may be related to the fact that the corresponding velocity distribution under the non-relativistic momentum distribution is a little flatter than that under the relativistic momentum distribution.[21]However, in the considered range of Epthe SPeunder non-relativistic distribution is at most 6.5%lower than that under relativistic distribution.Similar results are found for many other plasma cases when Teis high enough. This makes η close to each other in the two kinds of momentum distribution. In other words,our previous result of η in Ref. [14] is appropriate even if the nonrelativistic distribution was used for the electron when Teis very high.

4. Fitting formula of η and comparison with other works

According to Eq.(1),lots of calculations have been made to get η in the ranges of both Tiand Tefrom 0.1 keV to 100 keV, and ρ between 1. and 103g/cc. By fitting these data a formula of η is found as

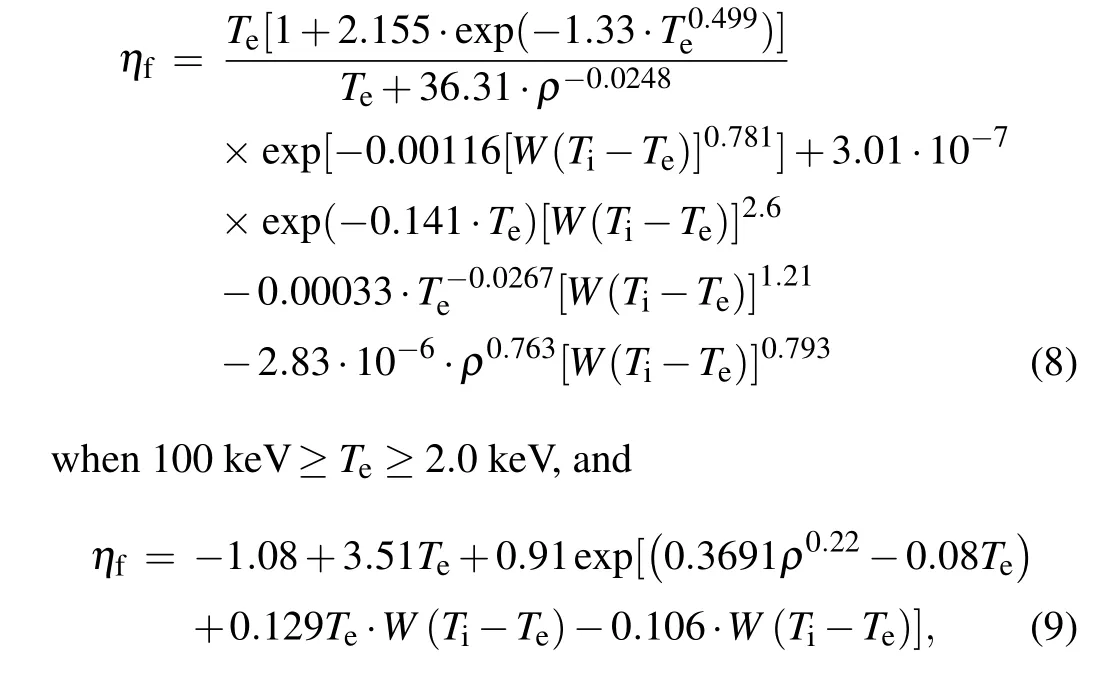
when Te＜2.0 keV. Here W(x)=0 if x ＜0, otherwise it is equal to x.

For the fitting results, there are some errors defined as 1-ηf/η, where ηfis the fitting value of η. Figure 3 plots the error as a function of Teand ρ when Ti=Te. Generally speaking, the error decreases with the increase of Tewhen ρ is fixed. The less absolute value of error when Te＞30 keV is not plotted in the figure. It is easy to see that in most cases the size of the error is less than 5%,and it may exceed 7%when Te＜5 keV and ρ ＞350 g/cc. Its maximum may be 15% at Te=2.0 keV and ρ ＞350 g/cc,where η(≈0.05)is small.

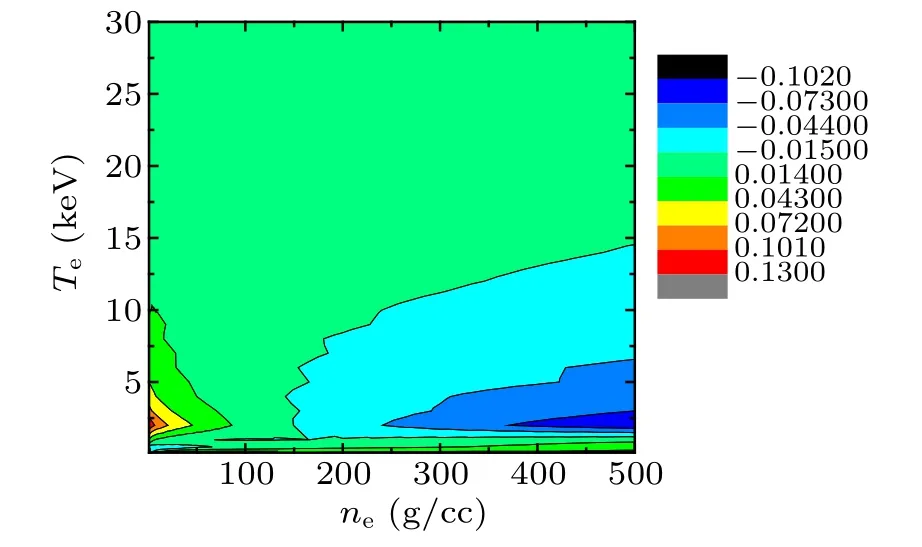
Fig.3. Error as a function of Te and ρ when Ti=Te.

Figure 4 shows the error as a function of Te, Ti, and ρ when Ti＞Te. This figure indicates that the size of the error is less than 3%in most cases. The error may become 10%,even 15% when Teis around 2.0 keV while both Tiand ρ are in a very narrow range of theirs. However, in this case η is small and less than 6.0%. Hence, totally speaking, the fitting formula is reliable in most cases where the size of the error is less than 5%, and the error may become 10%–15% only when Teis around 2.0 keV and both Tiand ρ are in very narrow ranges and η is less than 6.0%in this situation.

Fig.4. Error as a function of Te,Ti,and ρ when Ti ＞Te.

Fig.5. Electron–ion energy partition fraction comparison among our calculation,fitting and Fraley’s result when Te=Ti and ρ =0.213 g/cc.

It is necessary to compare the fitting formula with those obtained by others. In the case of Te=Tiand ρ =0.213 g/cc,figure 5 shows the energy partition fraction comparisons among our calculation, fitting and Fraley’s result.[6]Our calculation is according to Eq.(1)and the fitting is based on the fitting formulas(8)and(9). The fitting result is very close to the calculation when Teis small but the difference increases gradually with the increasing of Te. The fitting expression is close to Farley’s[6]η=Te/(Te+32)and their results are close to each other, especially at the low temperature range. Fraley’s expression gives η =0.238 at Te=Ti=10 keV while η =0.217 and ηf=0.210 are estimated by our calculation and fitting formula. When DT ions obtain half of the incident energy,namely η=0.5,Teis 37.7 keV according to our result,that is a few higher than 32 keV by Fraley’s work. The fitting formula gives ηf=Te/(Te+36.31·ρ-0.0248)at Te≥2.0 keV and Te=Ti. Thus ηf=Te/(Te+34.3) at ρ =10.0 g/cc and ηf=Te/(Te+32.4) at ρ =100.0 g/cc. Such tendency of ηfwith ρ and Teagrees with those in Fig. 1(b) in Ref. [6] and Fig. 11.14 in Ref. [8] but the formula is apparently different from Eq. (11.90) in Ref. [8], where η =Te/(Te+25) when ρ =10.0 g/cc～100.0 g/cc. Our results show η =0.231 and ηf=0.225 at Te=Ti=10.0 keV and ρ =10.0 g/cc. For the same Teand Tibut ρ=100.0 g/cc,η=0.245,and ηf=0.236.In both cases AM gave η =0.285.[8]So in general,our result is closer to Fraley’s than to AM’s.

The difference among ours,Fraley and AM is mainly due to the choice of the Coulomb logarithm logΛ in respective calculation. The choice is a little arbitrary in their calculations while no such arbitrariness exists in our model. In Fraley’s work[6]the following expression was used:

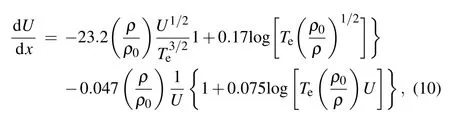
where U=E/E0,ρ0=0.213 g/cc,Teis measured in unit keV.In the above expression the first term and the second term of the right side represent the energy deposition in electron and DT ion,respectively. AM[8]used the following formula to get η:

where logΛ due to electron and DT ion are expressed as

According to Eq. (10) a similar expression with Eq. (11) can be obtained only with different Λeand ΛiTherefore, all the related Coulomb logarithms used in the two works are quite different. This leads to the difference of their results.

In summary, on the basis of our previous work, a fitting formula is obtained for electron–ion energy partition fraction for 3.54-MeV fusion alpha particles in DT plasmas as a function of plasma mass density ρ,electron temperature Te,and ion temperature Ti. In the formula,ρ varies between 1.0 g/cc and 10.03g/cc,and both Teand Tichange from 0.1 keV–100.0 keV.It covers a wide range of the plasma state. The formula is reliable in the above-mentioned range,and the error is less than 5%in most cases while the maximum error may reach 10%–15%only when Teis around 2.0 keV with ρ and Tivarying in a small range. Relativistic effect for electrons is investigated with the consideration of the projectile recoil in the plasmas at Te≥50.0 keV.Little influence of the effect is found upon the results of partition fraction. The fraction at Te＞Tiis close to that at Te=Ti. The comparisons with other fitting results are made at some plasma density at Te=Ti,and the difference is explained. Our formula is convenient for the simulation of alpha heating in inertial confined fusion hot dense DT plasmas.