Analysis of the Possible D(2317)and D∗2460)Molecules with QCD Sum Rules∗

Zun-Yan Di(狄尊燕),Zhi-Gang Wang(王志刚), and Guo-Liang Yu(于国梁)

1Department of Physics,North China Electric Power University,Baoding 071003,China

2School of Nuclear Science and Engineering,North China Electric Power University,Beijing 102206,China

AbstractIn this article,we assume that there exist the pseudoscalar D¯D∗s0(2317)and D∗¯D∗s1(2460)molecular states Z1,2and construct the color singlet-singlet molecule-type interpolating currents to study their masses with the QCD sum rules.In calculations,we consider the contributions of the vacuum condensates up to dimension-10 and use the formulato determine the energy scales of the QCD spectral densities.The numerical results,MZ1=4.61+−00..1018GeV and MZ2=4.60+−00..0076GeV,which lie above the D(2317)and D∗(2460)thresholds respectively,indicate that the D¯D∗s0(2317)and D∗¯D∗s1(2460)are difficult to form bound state molecular states,the Z1,2are probably resonance states.

Key words:molecular state,QCD sum rules

1 Introduction

In the recent years,many new charmonium-like and bottomonium-like exotic mesons[1](being bosons like the traditionalmesons),have been observed experimentally,and are labeled as the XY Z states.[2]These exotic states,with growing evidences,cannot be the pureorstates and are considered as good candidates for tetraquark states,which do not fit into the conventional quark model picture.[3]In order to decipher their underlying structure,a number of interpretations have been proposed,such as the molecules,[4−5]the tetraquark states,[6]the hybrid mesons,[7]the kinematical effects,[8]and so on.

In the molecular picture,a four-quark state is explained as a weakly bound state of two mesons.[9]Each constituent meson is bound internally by strong QCD color forces,while the mesons bind to each other by means of a much weaker color-neutral residual QCD force,analogous of the van der Waals attraction in chemistry.Among these observed XY Z states,some lie remarkably close to the meson-meson thresholds.Therefore,the molecular interpretation seems plausible for these states.The most impressive example is the original exotic state,the X(3872),[10]which has been investigated as the Dmolecular state by many theoretical groups,[4,11]owing to its mass with mX(3872)−mD∗0−mD0=+0.01±0.18 MeV.The Zc(3900),observed by the BESIII collaboration firstly in 2013,[12]is also close to the threshold of D¯D∗,and is taken as the isovector partner of the established isoscalar bound molecular state X(3872)with the same quantum number JP=1+in Refs.[13–14].Interestingly,the observed bottomonium-like states Zb(10610)and Zb(10650)by the Belle collaboration,[15]own the same near-threshold nature and are interpreted successfully as the B¯B∗and B∗molecular states.[16]The successes of the molecular interpretation for some observed exotic states stimulate the further theoretical studies on the analogous opencharmed meson pair system as a bound molecular state,which make several predictions of the possible molecules.

In theoretical techniques,the QCD sum rules method is a powerful tool in studying the hidden-charm(bottom)tetraquark or molecular states and hidden-charm pentaquark states.Here,we make the assumption that there exist the pseudoscalar D(2317)and D∗(2460)molecular states,and study their masses with the QCD sum rules to check the existence of the corresponding molecular states. The D and D∗mesons have negative parity,while the parity is positive for the(2317)and(2460)mesons.Based on the theoretical analysis in Ref.[17],there is a Coulomb-like force by exchanging a kaon in S-wave,that might be able to bind the D(2317)and D∗(2460)systems,respectively.In addition,the mass difference between the D(D∗)and)is close to the kaon mass,which means that the exchanged kaon will be near the mass shell and the range of the interaction will be unusually large.These are the reasons why we are interested in the D(2317)and D∗(2460)molecules.In calculations,we consider the contributions of the vacuum condensates up to dimension-10,and use the formulato determine the energy scales of the QCD spectral densities,[13]which can enhance the pole contributions remarkably and improve the convergent behaviors of the operator product expansion in the QCD sum rules for the exotic hadrons.[18]

The rest of this article is arranged as follows.In Sec.2,we consider the D(2317)and D∗(2460)systems as the pseudoscalar molecules,construct the corresponding color singlet-singlet molecule-type interpolating currents,and extract their masses and pole residues with the QCD sum rules.The numerical results and discussions are performed in Sec.3.The last section is reserved for our conclusion.

2 QCD Sum Rules for the Possible D(2317)andD∗(2460)Molecular States

Based on our assumption that there exist the pseu-doscalar D(2317)and D∗(2460)molecular states,the corresponding color singlet-singlet molecule-type interpolating currents are written as

respectively,where a,b are color indexes,and q denotes an up or down quark.

In QCD sum rules,we consider the two-point correlation functions

which can be obtained in two ways:on the phenomenological side and at the quark level.

On the phenomenological side,we insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators J1,2(x)into the correlation functions Π1,2(p)to obtain the hadronic representations.After isolating the ground state contributions from the pole terms,we get the following results

where the Z1,Z2denote the ground states,provisionally,considered as the D(2317),D∗(2460)molecules,respectively,and the pole residues λZ1,2are defined by⟨0|J1,2(0)|Z1,2(p)⟩= λZ1,2,which show the couplings of the currents J1,2to the states Z1,2.

At the quark level,we calculate the two-point correlation functions Π1,2(p)via the operator product expansion method in perturbative QCD.We contract the q,s and c quark fields with the Wick theorem and obtain the following results:

where the Qab(x),Sab(x),and Cab(x)are the full q,s and c quark propagators,respectively,

tn= λn/2,the λnis the Gell-Mann matrix,and Dα=∂α− igsGnαtn.[19]Then we compute the integrals in the coordinate space for the light quark propagator and in momentum space for the charm quark part.In the operator product expansion,we take into account the contributions of vacuum condensates up to dimension-10,assume vacuum saturation for the higher dimensional vacuum condensates,and keep terms which are linear in the strange quark mass ms.The vacuum condensates are the vacuum expectations of the operators On(αks).We take the truncations n≤10 and k≤1 for the operators in a consistent way,and discard the perturbative corrections.In Eqs.(6)–(7),we retain the termsandoriginate from the Fierz re-arrangement of theto absorb the gluons emitted from the heavy quark lines so as to extract the mixed condensates and four-quark condensatesand g2srespectively.One can consult Ref.[20]for some technical details about the operator product expansion.Once the analytical expressions of the correlation functions Π1,2(p)are obtained,the QCD spectral densities ρ1,2(s)are given by the imaginary parts of the correlation functions:ρ1,2(s)=ImΠ1,2(s)/π.According to the quark-hadron duality,we match the correlation functions Π1,2(p)obtained on the phenomenological side and at the quark level below the continuum thresholds s0,and perform Borel transform with respect to the variable P2=−p2to obtain the following QCD sum rules:

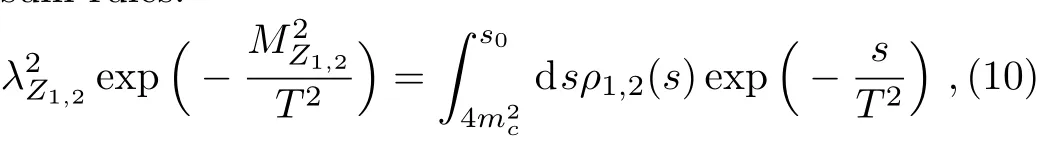
where

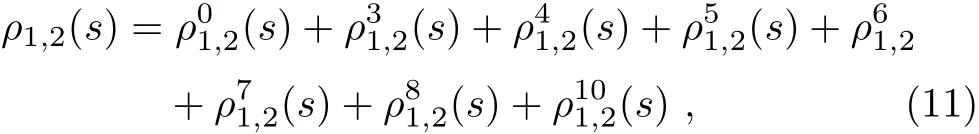
the superscripts 0,3,4,5,6,7,8,10 denote the dimensions of the vacuum condensates,and the T2denotes the Borel parameter.The explicit expressions of the spectral densities ρ1,2(s)are collected in the appendix.

To extract the masses of the states Z1,2,we take the derivative of Eq.(10)with respect to 1/T2and eliminate the pole residues λZ1,2:

3 Numerical Results and Discussions

In this section,we perform the numerical analysis.To extract the numerical values of MZ1,2,we take the standard values of the vacuum condensates(0.33GeV)4at the energy scale µ =1 GeV,[19,21−22]choose themasses mc(mc)=(1.28±0.03)GeV,ms(µ=2 GeV)=(0.096+0.008−0.004)GeV from the Particle Data Group,[2]and neglect the up and down quark masses,i.e.,mu=md=0.Moreover,we take into account the energy-scale dependence of the input parameters on the QCD side from the renormalization group equation,

where

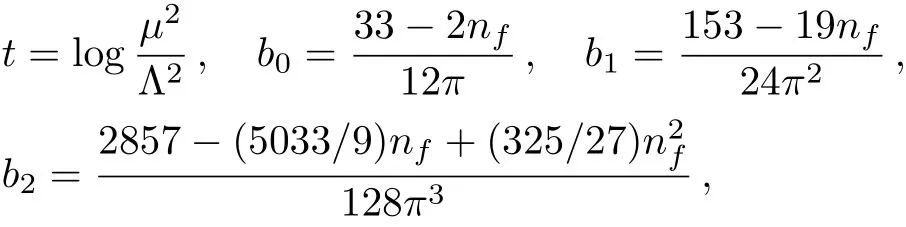
Λ=213 MeV,296 MeV,and 339 MeV for the fl avors nf=5,4,and 3,respectively.[2]For the hadron mass,it is independent of the energy scale because of its observability.However,in calculations,the perturbative corrections are neglected,the operators of the orders On(αks)with k>1 or the dimensions n>10 are discarded,and the higher dimensional vacuum condensates are factorized into lower dimensional ones therefore the energy-scale dependence of the higher dimensional vacuum condensates is modified.In addition,the variation of the heavy mass mcdepending on the energy scale leads to change of integral range 4m2c−s0of the variable ds.So we have to consider the energy-scale dependence of the QCD sum rules.

The hidden-charm four-quark systemcould be described by a double-well potential with two light quarkslying in the two wells respectively.In the heavy quark limit,the c quark can be taken as a static well potential,which binds the light quark q′to form a diquark in the color antitriplet channel or binds the light antiquarkto form a meson in the color singlet channel(or a meson-like state in the color octet channel).Then the hidden-charm four-quark states are characterized by the effective heavy quark mass Mcand the virtualityThe effective mass Mchas uncertainties,the optimal value in the diquark-antidiquark system is not necessary the ideal value in the meson-meson system.It is natural to take the energy scaleµ=V.In this article,we use the energy-scale formula:

with the updated value of the effective c-quark mass Mc=1.85 GeV in the meson-meson molecular system to determine the ideal energy scales of the QCD spectral densities.[23]For a better understanding of the energyscale dependence in Eq.(14),one can refer to Refs.[13,20,24],where the authors study the energy-scale dependence of the QCD sum rules for the hidden-charm tetraquark states and molecular states in detail,and suggest the above energy-scale formula for the first time.In our calculations,we observe that the values of the masses MZ1,2decrease slightly with increase of the energy scalesµfrom QCD sum rules in Eq.(12),while Eq.(14)indicates that the values of the masses MZ1,2increase when the energy scalesµincrease.Thus there exist optimal energy scales,which lead to reasonable masses MZ1,2.

In Eq.(12),there are two free parameters:the Borel Parameter T2and the continuum threshold value s0.The extracted hadron mass is a function of the Borel parameter T2and the continuum threshold value s0.To obtain a reliable mass sum rule analysis,we impose two criteria on the hidden-charm molecules to choose suitable working ranges for these two free parameters.The first criterion is the pole dominance on the phenomenological side,which require the pole contributions(PCs)to be about(40−60)%.The PC is defined as:

The second criterion is the convergence of the operator product expansion.To judge the convergence,we calculate the contributions of the vacuum condensates D(n)in the operator product expansion with the formula:

where the index n denotes the dimension of the vacuum condensates.

To search for the continuum threshold value s0more accurately,we take into account the mass gaps between the ground states and the first radial excited states,which are usually taken as(0.4−0.6)GeV in the four-quark sector.For examples,the Z(4430)is tentatively assigned to be the first radial excitation of the Zc(3900)according to the analogous decays,Zc(3900)±−→ J/ψπ±,Z(4430)±−→ ψ′π±and the mass differences MZ(4430)−MZc(3900)=576 MeV,Mψ′− MJ/ψ=589 MeV;[25]the X(3915)and X(4500)are assigned to be the ground state and the first radial excited state of the cs¯c¯s fourquark states,respectively,and their mass difference is MX(4500)−MX(3915)=588 MeV.[26]The relation

serves as a constraint on the masses of the hidden-charm four-quark states.

In Fig.1,we show the variations of the pole contributions with respect to the Borel parameters T2for different values of the continuum thresholds s0at the energy scalesµ=2.7 GeV and 2.7 GeV for the states Z1and Z2,respectively.From the fi gure,we can see that the values≤4.9 GeV are too small to satisfy the pole dominance condition and result in reasonable Borel windows for these two states Z1,2.To warrant the Borel platforms for the masses,we take the values T2=(3.7−4.1)GeV2for the state Z1and T2=(3.6−4.0)GeV2for the state Z2,respectively.In the above Borel windows,if we choose the values,the PCs are about(42−60)%and(42−61)%for the Z1,2,respectively.The pole dominance condition is well satisfied.

In Fig.2,we plot the absolute contributions of the vacuum condensates|D(n)|in the operator product expansion at central values of the above input parameters for the states Z1,2.From the fi gure,we can observe that the dominant contributions come from the perturbative terms D(0)for the Z1,2.The contributions of the other vacuum condensates are tiny.The convergent behavior in the operator product expansion is very good.

Thus,we obtain the Borel parameters,continuum thresholds and the pole contributions for the states Z1,2,which are shown explicitly in Table 1.Taking into account all uncertainties of the input parameters,we obtain the values of the masses and pole residues of the states Z1,2,which are shown in Table 1 and Figs.3–4.From Table 1,we can see that the energy-scale formulaµ=a nd the relationMX/Y/Z+(0.4−0.6)GeV are also well satisfied.

Fig.1 The pole contributions with variations of the Borel parameter T2and the continuum threshold value s0.

Table 1 The energy scales,Borel parameters,continuum threshold parameters,pole contributions,masses and pole residues for the molecular states.

Fig.2 The absolute contributions of the vacuum condensates with dimension n in the operator product expansion.

Fig.3 The masses with variations of the Borel parameters T2.

Fig.4 The pole residues with variations of the Borel parameters T2.

In the process of searching for the optimal Borel parameters and threshold parameters,we went through a series of attempts and corrections.Now we take a short digression to illustrate this procedure in more detail.Taking the state Z1as an example, firstly,we set MZ1=4.2 GeV tentatively and obtain the energy scaleµ=2.0 GeV according to the energy scale formula.√Then we take the continuum threshold parameter to be=(4.2+0.5)GeV as the energy gap between the ground state and the first radial excited state is about(0.4−0.6)GeV,and obtain the predicted masses MZ1,pole contributions and the contributions of the vacuum condensates up to dimension-10.

We observe that the predicted masses MZ1are much larger than 4.2 GeV and the pole contributions are much smaller than 50%in the region where the Borel platform appears,furthermore,the contributions of the vacuum condensates of dimension 10 are not small enough.Then we choose the mass MZ1>4.2 GeV,meaning MZ1=4.3 GeV,4.4 GeV,...and reiterate the same procedure until obtain the ideal Borel parameters and continuum threshold parameters.Finally,the predicted masses MZ1,2and pole residues λZ1,2obtained by us are quite reliable.

The central value MZ1=4.61 GeV is about 260 MeV above the threshold=1870+2480=4350 MeV,where the mass of the¯D∗s0(2317),=2480 MeV,is taken from the computed results of S.Godfrey and K.Moats about excited charm and charmstrange mesons in Ref.[27],while the central value MZ2=4.60 GeV is about 130 MeV above the thresholdThe numerical results indicate that the D¯D∗s0(2317)and D∗(2460)are difficult to form bound state molecular states.

In Refs.[28–29],the authors studied the analogous heavy meson systems.In Ref.[28],Liu,Luo and Zhu studied the S-wave Ds(2317)system through the heavy meson chiral perturbation theory,considering the η meson exchange between Dsand(2317),which generates a potential to bind them,and observe that there exists the DsD(2317)molecular state.In Ref.[29],similarly,using the heavy meson chiral perturbation theory,Sanchez et al.studied the S-wave DDs∗0(2317)and D∗Ds∗1(2460)systems exchanging a kaon to bind D(D∗)and Ds∗0(Ds∗1),and predicted the existence of DDs∗0(2317)and D∗Ds∗1(2460)bound states.differently,in this article,we construct the color singlet-singlet molecule-type interpolating currents J1,2(x)in Eqs.(1)–(2)to study the D(2317)and D∗(2460)systems with QCD sum rules,and give the prediction that the D(2317)and D∗(2460)are diffi cult to form bound state molecular states.

Furthermore,the Z1,2are probably the resonance states,since the constructed color singlet-singlet currents J1,2(x)may not necessarily correspond the D(2317)and D∗(2460)bound state molecular states,and could couple potentially to the D(2317)and D∗(2460)scattering states,respectively.At the phenomenological side,we can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators J1,2(x)into the correlation functions Π1,2(p)to obtain the hadronic representations.After isolating the D(2317)and D∗(2460)scattering states,we get the following results

the εµare the polarization vectors of the D∗and.

We rewrite the correlation functions Π1,2(p)into the following forms through dispersion relation,

In this article,we choose the value,the QCD sum rules can be written as

where we introduce a coefficient κi,if κi= 1,the QCD sum rules can be saturated by the scattering states(2317)and D∗(2460),respectively.The input parameters are taken as MD=1.87 GeV,MD∗=2.01 GeV,=2.46 GeV,[2]=2.48 GeV,[27]fD=0.208 GeV,fD∗=0.263 GeV,f=0.333 GeV,=0.245 GeV,[30]s0=5.12GeV2.In Fig.5,we plot the coefficient κiwith variation of the energy scaleµat T2=3.9 GeV2and 3.8 GeV2for the Z1,2,respectively.At the vicinities of the energy scaleµ=2.3 GeV and 1.1 GeV,κi≈ 1,however,from the fi gure,we can see that the coefficient κidecreases monotonously with increase of the energy scaleµ.The reliable QCD sum rules do not depend heavily on the energy scaleµ.So,the QCD sum rules can not be saturated by the scattering states D2317)and D∗(2460),respectively.

Fig.5 The coefficient κiwith variation of the energy scale µ.

In the following,we perform Fierz re-arrangement for the currents J1,2both in the color space and Dirac-spinor space to obtain the results,

We cannot distinguish those contributions to study them exclusively.Hence,we infer that the Z1,2are particular resonance states,which are the special superpositions of the scattering states,molecular states and moleculelike states,and embody the net effects.Moreover,for the meson-meson scattering states such as ηcK∗0,χc0K,J/ψK1,...lying below the Z1,the Z1can decay to them easily through fall-apart mechanism,and the de-cays contribute a finite width to the Z1.Now,we discuss an effect of the finite width on the predicted mass MZ1.We consider the contributions of the meson-loops to the correlation function Π1(p),as the current J1(x)has non-vanishing couplings with the scattering states ηcK∗0,χc0K,J/ψK1,etc.

The finite width effect is considered through the following simple change in the hadronic spectral density,

where

We take the central values of the input parameters,and ΓZ1=300 MeV(not small).Then the phenomenological side of the QCD sum rules in Eq.(10)changes as follows

where the BT2denotes the Borel transformation.The numerical factor 0.70 can be absorbed safely into the pole residue λZ1.Therefore,in this article,when we take the zero width approximation in Eq.(4),the predicted masses MZ1,2are reasonable.

4 Conclusion

In this article,we assume that there exist the pseudoscalar D¯D∗s0(2317)and D∗¯D∗s1(2460)molecular states Z1,2,and study their masses with the color singlet-singlet interpolating currents through the QCD sum rule approach.In calculations,we carry out the operator product expansion up to the vacuum condensates of dimension 10 and use the formuladetermine the energy scales of the QCD spectral densities.The numerical results show that the central value of the state Z1,MZ1=4.61 GeV,is about 260 MeV above the D(2317)threshold,while,in the case of the Z2,the central value MZ2=4.61 GeV is about 130 MeV above the D∗(2460)threshold,which indicate that the D(2317)and D∗(2460)are difficult to form bound state molecular states.The Z1,2are probably particular resonance states,which are the special superpositions of the scattering states,molecular states and molecule-like states,and embody the net effects.We expect that these results in our work could be helpful for investigating the Z1,2experimentally,and would be able to be testified in the future experiments,such as BESIII,LHCb,and Belle-II.

Appendix

The explicit expressions of the QCD spectral densities ρ1,2(s),

where