基于脑电信号特征提取的睡眠分期方法研究

刘 戈，刘洪运，石金龙，王国静，胡敏露，王卫东*

（1.解放军总医院海南医院，海南三亚 572013；2.解放军总医院医学创新研究部，北京 100853）

0 引言

睡眠是一项非常重要的生命过程，但至今人们对其了解甚少。关于睡眠的研究最早在20 世纪30年代，德国精神病学家Berger[1]发现人在睡眠和清醒期（wakefulness，W）的脑电（electroencephalogram，EEG）活动呈现不同的节律。1953 年，Aserinsky 等[2]发现了快速眼动（rapid eye movement，REM）睡眠与非快速眼动（non-rapid eye movement，NREM）睡眠。1968年，Rechtschaffen 和 Kales[3]提出 R&K 睡眠分期标准，将 NREM 期细分为 S1、S2、S3、S4 4 个阶段。S1、S2阶段为浅度睡眠期（light sleep，LS），S3、S4 阶段为慢波睡眠期（slow-wave sleep，SWS）。2007 年美国睡眠医学学会（American Academy of Sleep Medicine，AASM）将R&K 金标准中的 S1、S2 期相应更改为 N1（NREM 1）、N2（NREM 2）期，S3、S4 期合并为 N3（NREM 3）期。睡眠分期标准如图1 所示。

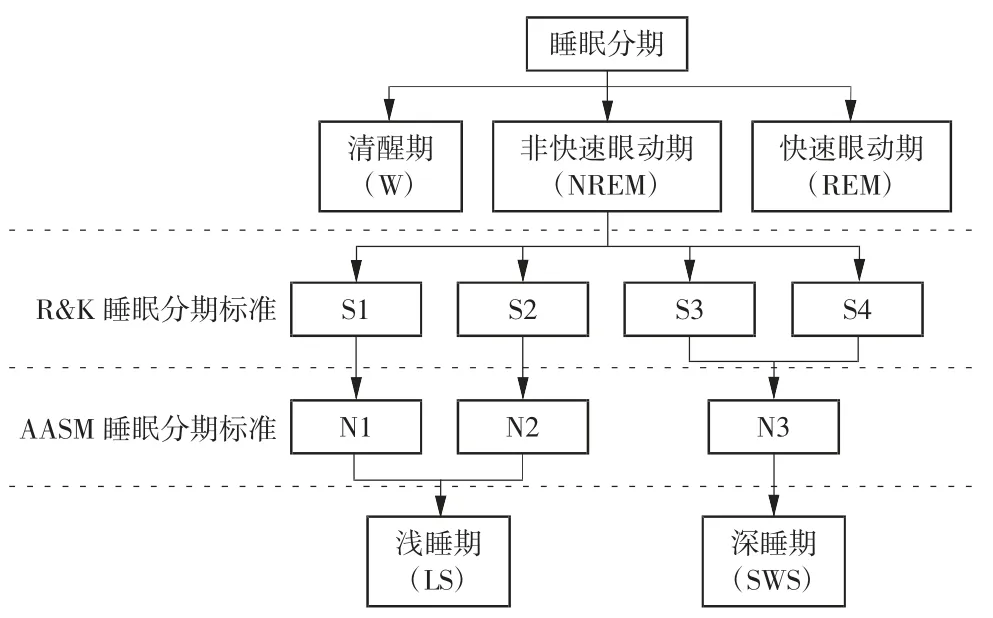
图1 睡眠分期标准

近年来，基于单通道EEG、多通道EEG、心电（electrocardiogram，ECG）、眼电（electro-oculogram，EOG）、肌电（electromyogram，EMG）和呼吸等生理信号提取特征并使用分类器进行睡眠分期研究的国内外学者越来越多。表1 列举了一些代表性研究，可以发现，对单一信号而言，基于EEG 的睡眠分期效果最好，ECG 次之，EOG 和 EMG 更差一些。因此，本文以分期准确率为重点，研究一种基于单通道EEG 特征提取的睡眠分期方法。

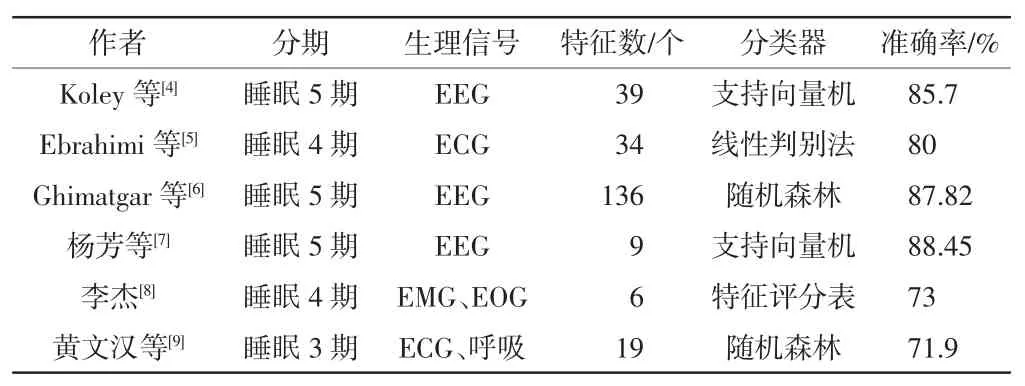
表1 睡眠分期国内外代表性研究

传统的睡眠EEG 特征提取方法主要有时域、频域、非线性分析方法。时域分析是出现最早且最直观的分析方法，频域分析仅能发掘信号的频域特征。这2 种分析方法对于EEG 这种非平稳、非线性信号而言存在一定的局限性。非线性分析方法，如样本熵、模糊熵、功率谱熵等适用于EEG 信号，但忽略了非高斯过程的某些有用信息，如相位信息。而高阶谱分析就可以发现睡眠EEG 的相位耦合信息。本文将在传统特征的基础上提取EEG 双谱特征、递归性特征和符号动力学特征，有针对性地补充传统特征未能表现的睡眠EEG 有用信息或改进传统特征的不足，组成一组信息表达较为全面的特征向量并使用分类器进行睡眠自动分期。

1 方法

本研究的技术路线如图2 所示，首先获取睡眠EEG 数据并进行预处理，然后使用各种特征提取方法获得EEG 样本的特征参量，使用支持向量机（support vector machine，SVM）作睡眠时相分类，最后经隐马尔可夫模型（hidden Markov model，HMM）学习睡眠阶段之间的过渡规则并对已分类得到的睡眠标签作修正，最终得到整夜睡眠分布及分期准确率。下面将对各部分进行具体介绍。

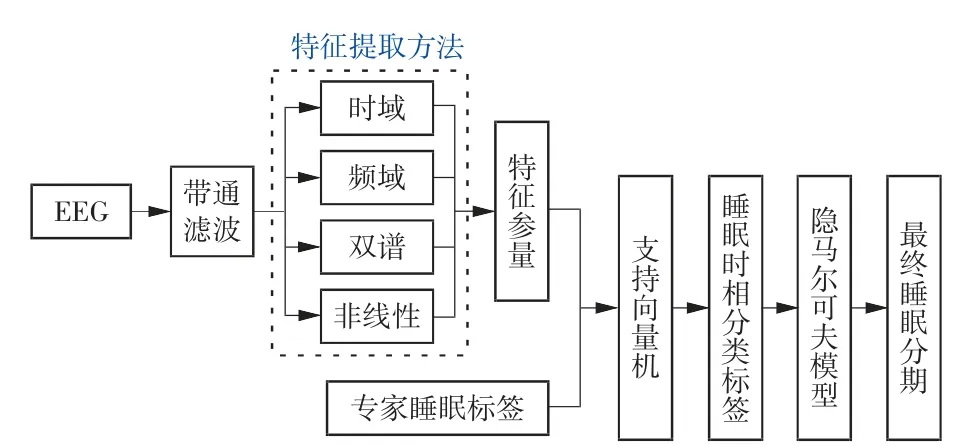
图2 基于单通道EEG 进行睡眠分期的技术路线图

1.1 数据获取和预处理

本文使用的睡眠EEG 数据来自于麻省理工学院（Massachusetts Institute of Technology，MIT）创建的睡眠生理信号开源数据库（网址为https://physionet.org/physiobank/database/sleep-edfx/）[10]。随机选取 10名受试者整夜睡眠实测数据，共10 组EEG 数据。其中6 组为健康志愿者的睡眠数据，另外4 组为有轻微失眠志愿者的睡眠数据。均使用Fpz-Cz 单导联EEG 信号，受试者包括3 名男性和7 名女性，年龄21～65 岁。测试过程中未使用任何药物进行干扰。采样频率均为100 Hz。睡眠分期结果由专家进行了人工标注（以R&K 睡眠分期标准标记），以专家标注结果作为标签来测试本文提出方法的分期准确性。定义30 s 的EEG 为一个样本，本文所选取的10 名受试者睡眠样本分布见表2。

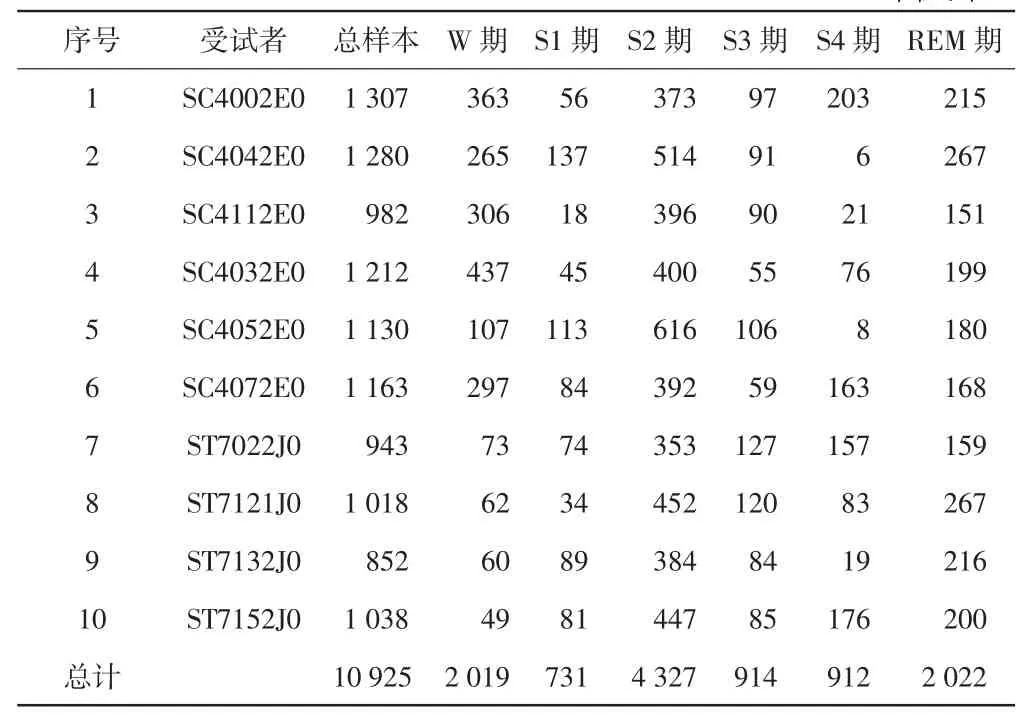
表2 受试者睡眠样本分布情况 单位：个

由于EEG 信号具有很强的变异性和随机性，且易受到其他生理信号和外界环境的干扰，所以需要对原始数据进行预处理以消除可能存在的噪声干扰。本研究选用0.5～47 Hz 的FIR（finite impulse response）带通滤波器对原始EEG 数据作去噪处理。

1.2 特征提取

本文提取了时域、频域、双谱、非线性特征共计48 个，详见表3。下面将着重介绍本研究中使用到的部分特征。

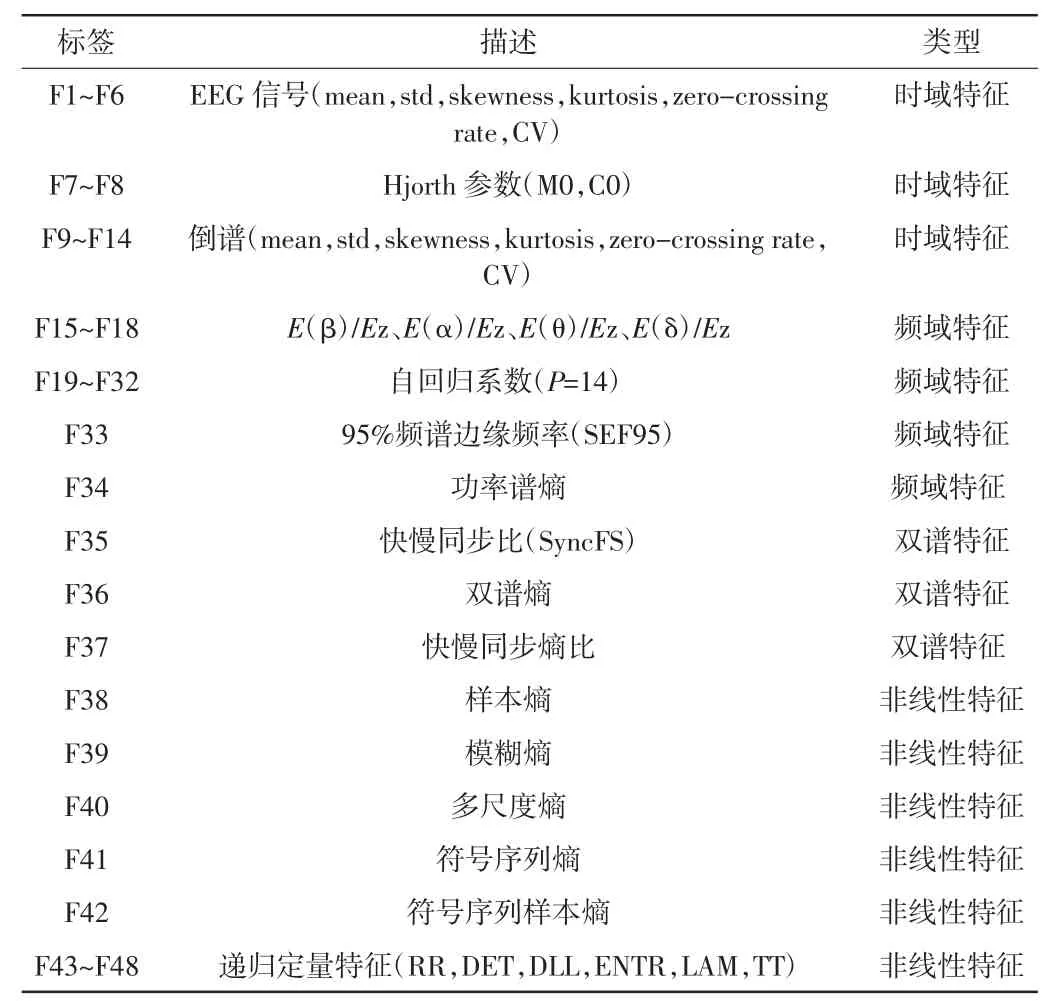
表3 特征列表

1.2.1 频域特征

使用自回归（auto-regression，AR）参数模型法求得EEG 的功率谱密度分布函数，分别求取0.5～4 Hz（δ 波）、4～8 Hz（θ 波）、8～13 Hz（α 波）和 13～30 Hz（β波）4 个频带的功率以及0.5～30 Hz 频率范围的总功率（Ez）。以4 种特征波占总功率的比值作为其频域的4 个特征。频域能量特征被证实是应用于睡眠分期的有效特征[7，11]。

将频域的功率谱密度与香农熵相结合，可得到功率谱熵。功率谱熵被发现对S2 期与SWS 期的区分有非常显著的意义[12]。功率谱熵的计算公式为

式中，Pi为频率值i 处的归一化功率谱密度。

95%频谱边缘频率（SEF95）是在功率谱密度分布函数的基础上，计算95%曲线下面积的频谱边界频率，指95%总功率谱处最高边界的频率。它将功率谱简化为单一的参数（即独立的观察指标），能够清楚地表示脑电图功率与频谱的移动。麻醉过程中的SEF95 值反映EEG 信号从清醒时候的高频波为主到麻醉后低频波占优势的过程。而与麻醉深入过程类似，在睡眠由浅入深的过程中，SEF95 值也会随着睡眠的加深而减小，REM 期又稍增大。图3 为SC4112E0 受试者的982 个睡眠样本6 个睡眠时相SEF95 值的平均值变化图，其规律性明显。说明SEF95 除可作为麻醉深度的指标外，还可作为睡眠深度判别的依据之一。

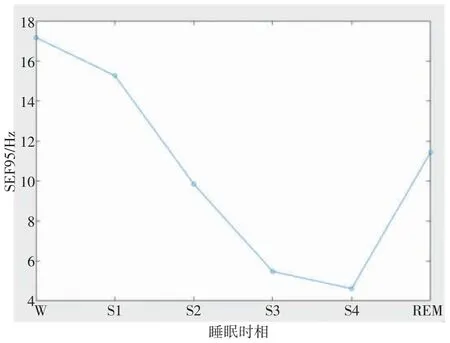
图3 SC4112E0 受试者睡眠6 期各期SEF95 平均值

1.2.2 双谱特征

为补充传统分析方法难以得到的EEG 信息或者改进传统特征的不足，本文引入了高阶统计量。高阶统计量是指阶数大于二阶的统计量，主要有高阶矩、高阶累积量和高阶谱等[13]。高阶统计量于传统特征而言，其优势在于：（1）高阶统计量可以展现EEG信号的相位耦合信息，而传统特征仅能展现EEG信号的幅值信息。（2）高斯过程三阶及以上累积量均为0，因此高阶统计量可以有效抑制信号的背景高斯噪声。

双谱（即三阶谱）是最常用、最简单的高阶谱。双谱是三阶累积量的二维傅里叶变换，其公式表示如下：

式中，f1、f2为归一化频率；τ1、τ2为三阶累积量 c3x的时延；ω1=2πf1，ω2=2πf2。双谱值 B 反映的是（ω1，ω2）处的幅值相位耦合能量。本文将在双谱值B 的基础上，进一步研究用于睡眠分期的定量特征。

（1）快慢同步比。

快慢同步比是应用于麻醉深度检测的EEG 双频指数（bispectral index，BIS）的子参数，能够定量反映不同频带信号相位耦合的程度[14]。在BIS 指数中，快慢同步比的定义为

式中，B0.5～47代表 EEG 整个频域 0.5～47 Hz 的双谱值之和；B40～47代表高频区域 40～47 Hz 的双谱值之和。两者之比取对数作为反映双谱分析中相位耦合信息的指标——快慢同步比。

基于前期的研究，定义用于睡眠分期的最优快慢同步比公式如下[15]：

式中，B0.5～40代表 EEG 频域 0.5～40 Hz 的双谱值之和，B10～40代表高频区域 10～40 Hz 的双谱值之和。

（2）双谱熵。

与功率谱熵类似，将香农熵应用到双谱域可得双谱熵[16]。双谱熵反映包含有相位耦合信息的双谱值的非线性特性，其计算步骤如下：

①计算求得EEG 信号的双谱值Bx（k1，k2）；

②计算各点双谱值占整个双谱域双谱值总和的概率：

③求出双谱熵：

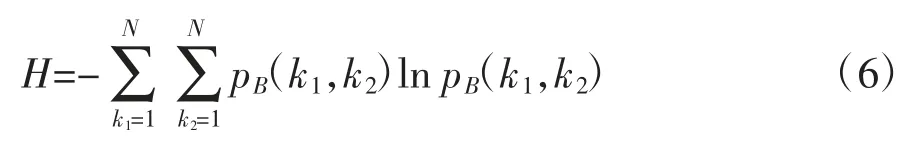
（3）快慢同步熵比。

基于双谱熵的计算方法，结合快慢同步比的定义，可定义快慢同步熵比，公式如下：

式中，H0.5～40表示在 0.5～40 Hz 频带内的双谱熵，H10～40表示在10～40 Hz 频带内的双谱熵。快慢同步熵比反映2 个双谱作用域的双谱熵的比值。

1.2.3 符号动力学与熵

研究表明，对比时域、频域和时频分析方法，采用非线性方法对非平稳EEG 信号作睡眠分期的效果最优[17]。而熵运算在非线性分析中占有重要地位。目前，以样本熵、模糊熵、多尺度熵为特征作睡眠时相划分是使用较普遍的一种方法。大量研究证明，这些熵对睡眠分期效果显著[18-20]。3 种特征具体的计算流程本文不再详述[7，20]。但传统熵存在其不足之处，主要包括：（1）传统熵值易受非平稳突变干扰的影响；（2）传统熵受序列概率分布的影响，从而导致其并非单纯反映序列的信息增长率。为了改进这些不足，本文使用了将符号动力学与熵运算相结合的生物电研究方法。具体步骤：首先，定义符号，对生物电信号进行符号粗粒化；其次，定义维数m 和时延τ，得到短符号序列[21]；最后，对短符号序列作不同的熵运算，可得符号化熵。符号化就是利用有限的符号实现数据的离散化。定义短符号序列的过程就是进行相空间重构，相空间重构后的字包含有相邻时间采样点的动态信息。因此，使用符号化熵作为睡眠分期的有效非线性特征以达到对生物电信号特征的有效提取和分析，本文中提取的符号化熵包括以下2 种：

（1）符号序列熵（F41）。

符号化序列求香农熵可得符号序列熵[22]。将原始时间序列符号化，得到符号序列Y，定义短符号字长（即维数m）为2、时延τ 为1 对符号序列进行相空间重构，得到符号嵌入矢量。对符号嵌入矢量中的所有短符号序列求熵即可得到符号序列熵。

（2）符号序列样本熵（F42）。

将原始时间序列符号化和相空间重构后得到的短符号序列求样本熵可得到符号序列样本熵。它与样本熵的计算相似，不同之处在于将样本熵中“嵌入矢量相似”的判断转化为“符号嵌入矢量相等”的判断[23]。

2 种符号化熵的计算流程图如图4 所示。

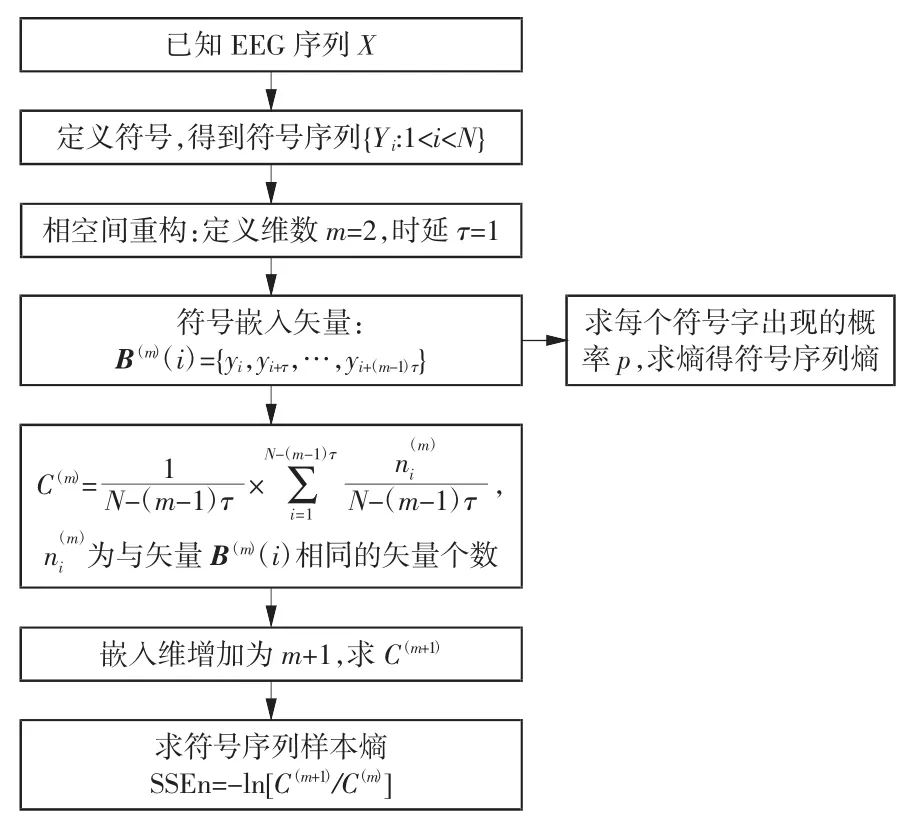
图4 2 种符号熵计算流程图

符号的定义可以有各种不同的方法，本文使用如下函数进行符号定义：

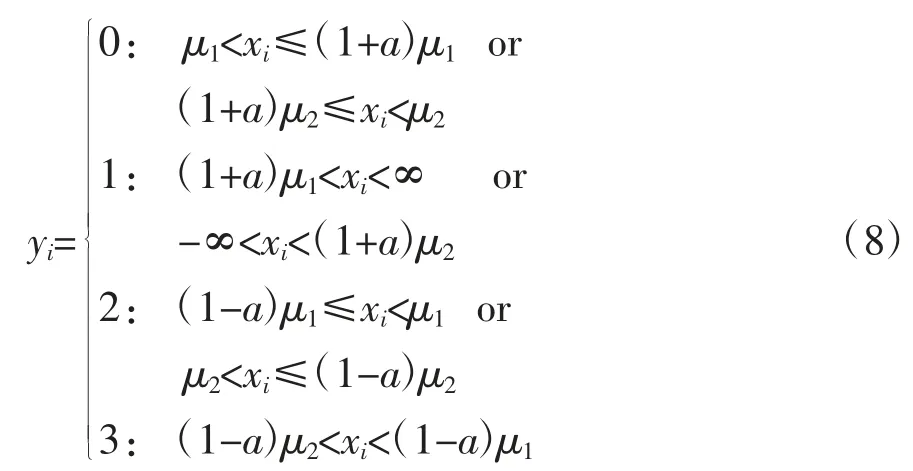
式中，xi为 EEG 序列 X 中的元素；yi为得到的符号序列Y 中的元素；μ1为原始序列X 中大于等于0 的取样信号的平均值；μ2为序列X 中小于0 的取样信号的平均值；a 是一个特殊的参数，其值过大会丢失原始数据的详细信息，过小会造成时间序列受噪声影响明显，通常情况下取a=0.05[24]。图5 为2 名受试者睡眠6 期符号序列样本熵均值图及组间统计学分析结果，可以发现，随着睡眠的加深，符号序列样本熵逐渐减小，S4 期达到最小，到REM 期又有大幅增加。对该特征做统计学分析，发现仅标注出的组间符号序列样本熵，无显著统计学差异（P＞0.05），其他各组间均有显著统计学差异。

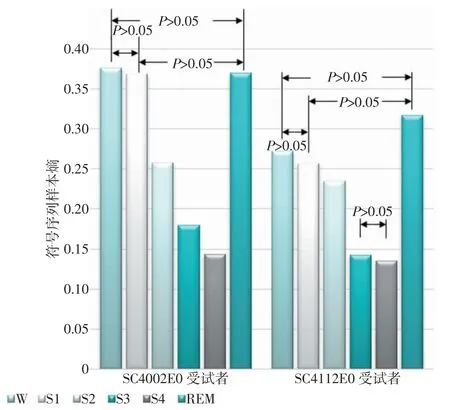
图5 2 名受试者睡眠6 期符号序列样本熵均值图

1.2.4 递归定量分析

递归性表述的是系统在特定时间状态具有相似性，是动态系统和非线性系统的基本特性之一。动力学系统可以用向量集表示，当动力学系统中的某2个特定时刻的向量之间的欧氏距离小于一定数值时，定义为递归。1987 年，Eckmann 等[25]第一次提出递归图（recurrence plot，RP）分析方法。若2 个时刻递归，定义为Ri，j=1，在递归图中表现为黑色；若2 个时刻非递归，定义为 Ri，j=0，在递归图上表示为白色。1994 年，Webber 等[26]首次提出用递归定量分析（recurrence quantification analysis，RQA）方法对递归图中的递归点和规则线段所占的比例进行定量分析。RQA 的主要量化参数有递归率（RR）、确定性测度（DET）、平均对角线长度（DLL）、递归熵（ENTR）、层状度（LAM）、捕获时间（TT）等。

在不同的睡眠时相，EEG 信号的递归特性不同，且呈现有规律的变化。图6 为随机选取的不同睡眠时相的30 s EEG 样本各12 个计算得到的6 个递归定量特征变化规律图。可以发现，由W 期到NREM 期，随着睡眠的不断加深，EEG 信号递归性增强，混沌性变弱，随机性减小，6 个定量特征值均逐渐增大，到S4期达到最大。在REM 期EEG 信号递归性减弱，6 个定量特征值又减小。本文使用RR、DET、DLL、ENTR、LAM、TT 这 6 种递归定量特征（F43～F48）作为睡眠自动分期的特征值。

1.3 SVM

本文选择台湾的林智仁教授在2001 年开发的一套成熟、使用非常普遍的SVM 库——Libsvm 工具包，采用径向基核函数进行非线性分类，同时使用网格搜索方法选取需要设置的2 个子参数c 和g，作多元分类。

使用Libsvm 工具包进行分类的步骤如下：

（1）按照Libsvm 工具包要求的格式准备数据集，要求格式为：＜label＞＜index1＞:＜value1＞＜index2＞:＜value2＞＜index3＞:＜value3＞……

（2）对数据做标准化处理。对数据集进行简单的缩放处理。缩放的主要目的为：①避免一些特征值范围过大而另一些特征值范围过小；②避免计算过程过于复杂。本文使用Z-score 标准化方法（又叫零-均值规范化、标准差标准化）处理数据，经过处理的数据的均值为0，标准差为1。Z-score 标准化的公式如下：

（3）应用径向基核函数（RBF 核函数）将输入样本映射到高维特征空间，解决在低维空间中线性不可分的问题。

（4）选择得到最优的c 和g。c 为惩罚因子，表示对类中离群样本的重视程度，c 值越大说明越重视离群样本；g 为核函数参数。c 和g 的选择对分类精度影响很大，在本研究中，使用SVMcgForClass 函数完成c 和g 的选择。

（5）用得到的最优c 和g 训练分类模型。使用Libsvm 工具包中的svmtrain 函数训练多分类模型。

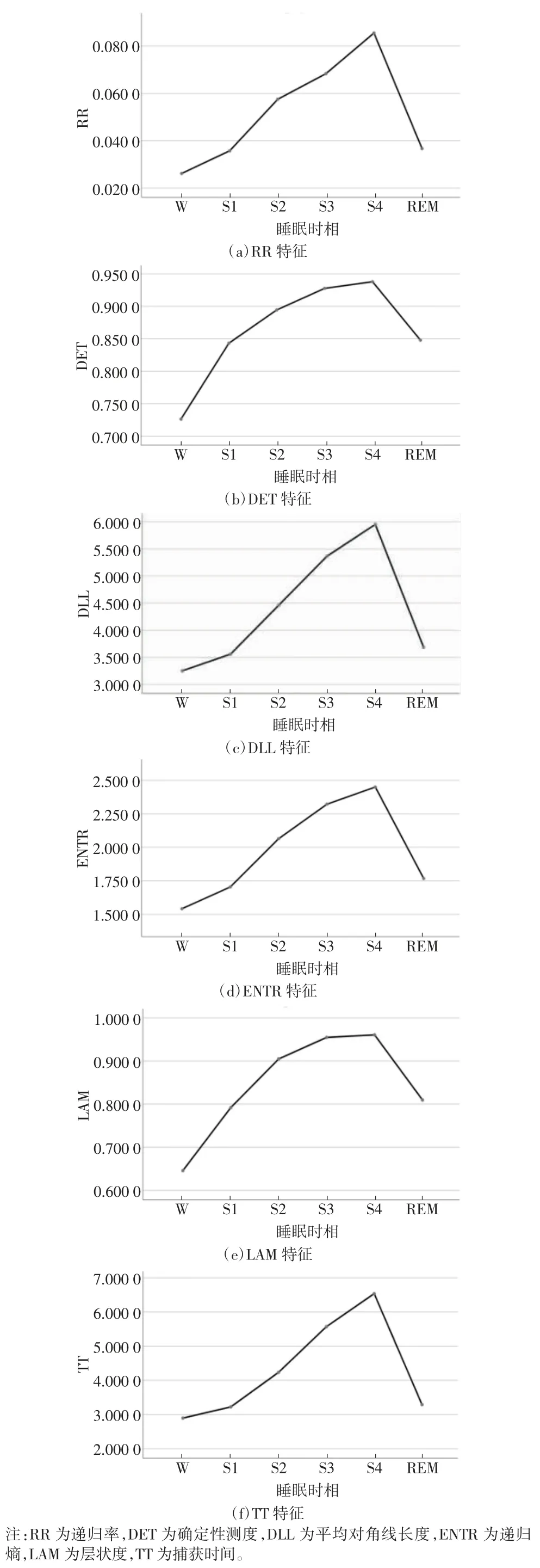
图6 睡眠6 期EEG 数据6 种递归定量特征均值变化图

（6）利用获得的模型进行测试。使用Libsvm 工具包中的svmpredict 函数测试分类的准确度。

1.4 隐马尔可夫模型

睡眠各阶段之间的过渡模式不是随机的和没有联系的，而是遵循一定的规则，如：从清醒状态不可能直接进入深度睡眠期。HMM 模型就是为了学习睡眠阶段的转换规则，减少分类产生的误差，提高睡眠分期的准确性。

本文中HMM 模型的具体表达如下：

（1）隐含状态C：受试者5、受试者10 的专家人工标注的R&K 标准睡眠分期标签，C={W，REM，S1，S2，S3，S4}。

（2）可观测状态 O：将表 2 中受试者 1～4、6～9 作为训练模型，分类得到的受试者5、受试者10 的睡眠 6 期分期标签，O={W，REM，S1，S2，S3，S4}。

（3）隐含状态概率转移矩阵A（Transmit_matix）：隐含状态的6 种睡眠时相间相互转变的概率矩阵。

（4）发射矩阵 B（Emission_matix）：即可观测状态转移矩阵，为可观测状态6 种睡眠时相间相互转变的概率矩阵。

基于HMM 模型作睡眠分期修正的流程如图7所示。

2 结果

将10 名受试者共计10 925 个睡眠样本整合在一起，总样本睡眠各期分布见表2。由于样本数据较多，使用90%的样本作为训练集进行SVM 分类模型的训练，另外10%作为测试集。睡眠6 期分类的测试准确率达85.06%。具体睡眠各期的分类结果见表4。

从表 4 中可以看出，W 期、S2 期、S4 期和 REM期分期准确率相对较高，分别为97.97%、91.68%、85.17%和82.50%。分期效果较差的是S1 期和S3 期，准确率仅为41.27%和60.42%，测试集总体的睡眠分期准确率达85.06%。在分期准确率较低的S1 期和S3 期中，S1 期有 25.40%的样本误分为 REM 期，有17.46%的样本误分为W 期；S3 期有27.08%的样本误分为S2 期，有7.29%的样本误分为S4 期。本文使用十折交叉验证提高结果的可靠性，十折交叉验证的平均准确率为83.68%。为使受试者睡眠分期结果更符合实际且改善个别睡眠时相分期结果较差的情况，本研究中增加了HMM 模型，构造了SVM-HMM睡眠自动分期模型提高睡眠分期的准确率。

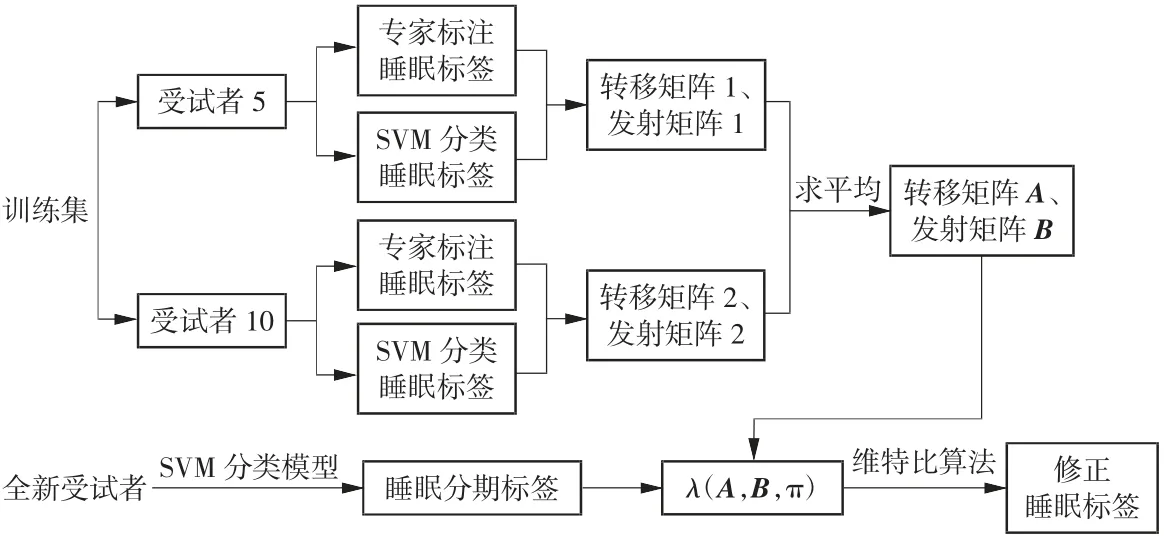
图7 睡眠分期修正HMM 模型流程图

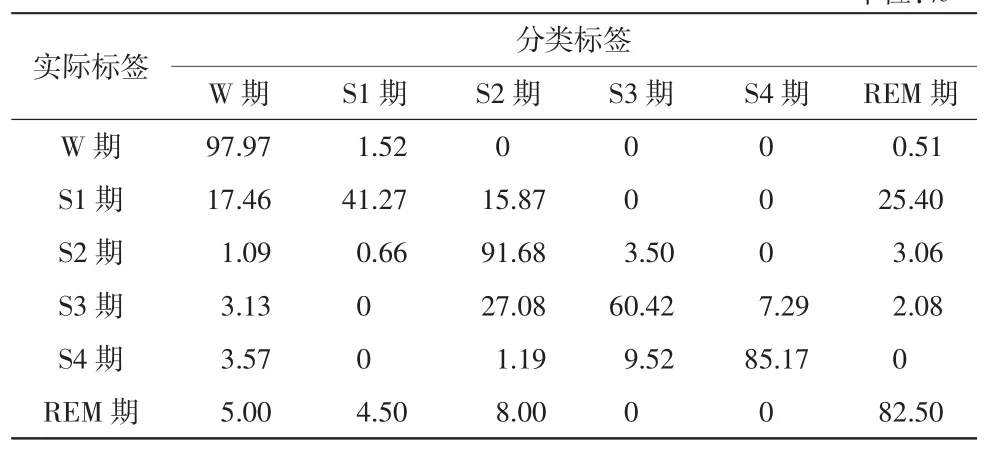
表4 10 925 个样本数据睡眠6 期测试结果（分类准确率）单位：%

将表2 中10 名受试者共计10 925 个睡眠样本作为训练集进行SVM 分类模型的训练，得出训练模型用于全新受试者ST7052J0 的整夜睡眠样本的睡眠时相分类，准确率为79.16%。再增加隐马尔可夫模型作睡眠分布修正后，得到睡眠6 期分期准确率为87.34%。睡眠分期结果如图8 所示。可以发现：（1）HMM 模型学习了睡眠阶段之间的转换规则，使分期结果较只使用SVM 分类器得到的分期结果更接近人的实际睡眠分布，能清晰地将睡眠时相的转换表达出来。（2）专家标注睡眠分布与经HMM 模型修正后的该受试者的睡眠分布一致性高。

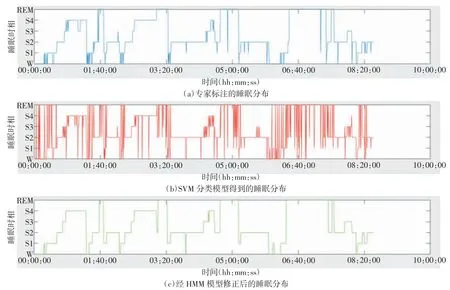
图8 ST7052J0 受试者睡眠实际分布与分类结果分布图

表5 给出了使用SVM-HMM 睡眠自动分期模型ST7052J0 受试者的睡眠分期结果。由表5 可以看出，该睡眠分期模型对于S2 期、S4期与REM 期的分期准确率分别为89.90%、99.21%和94.25%，准确率较高。对比表4 中睡眠分期的测试结果，S1 期和S3 期的分期准确率有了明显的提升，S1 期的分期准确率达到78.51%。说明HMM 模型的应用大大提高了睡眠分期的准确率，改进了部分睡眠时相分期结果较差的不足。在众多相关研究中，该模型对全新受试者睡眠6 期的分期准确率较高，说明该方法泛化能力较强，可以用于全新受试者的睡眠分期，具有潜在的临床价值。基于本文提出的SVM-HMM 睡眠自动分期方法得到的T7052J0 受试者的睡眠6 期分期准确率达87.34%。

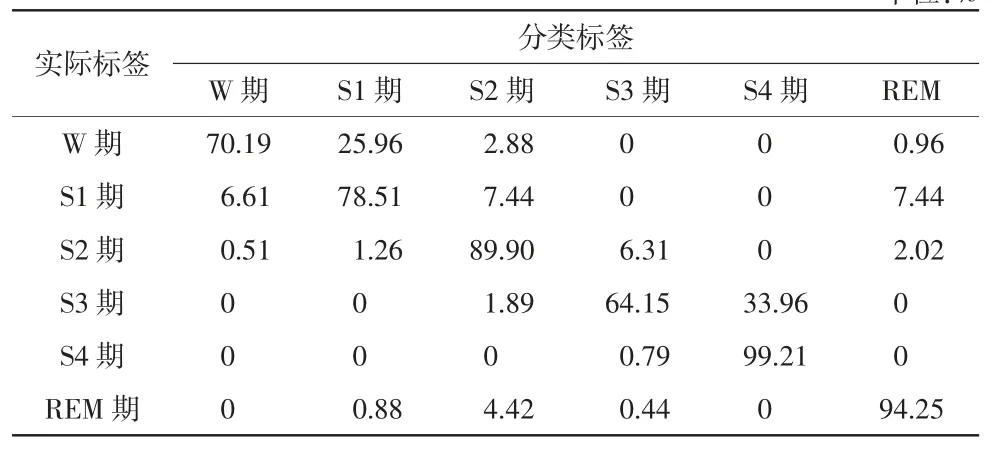
表5 ST7052J0 受试者睡眠6 期分类结果（预测准确率） 单位：%

3 结论与讨论

本文将研究的重点放在睡眠分期的特征提取及分期修正上，构造了一个基于EEG 信号特征提取的睡眠自动分期模型（SVM-HMM 模型）。在特征提取方面，创新性定义了应用于睡眠分期的双谱域快慢同步比、快慢同步熵比等双谱特征。将EEG 的95%边缘频率、递归定量分析特征、符号动力学与熵结合的特征（如符号序列样本熵、符号序列熵）用于睡眠分期。在传统特征的基础上，新增了EEG相位耦合特征、递归性特征和符号熵特征用于睡眠分期，并用样本数据证明了以上特征应用于睡眠分期的有效性。考虑睡眠分期的实际应用场景，将SVM-HMM 睡眠自动分期模型用于新的受试者ST7052J0 的整夜睡眠分期，睡眠分期结果与实际睡眠分布基本一致，睡眠6 期分期准确率为87.34%。实验结果证实了本文所提出的EEG 自动睡眠分期方法的可行性和有效性，且定义了几种可应用于睡眠分期的有效EEG 特征。

本研究避免了大量睡眠分期研究中数据样本量较小、不作交叉验证及局限于单一受试者样本进行训练并测试等问题。在样本量较大，使用十折交叉验证的情况下，所得模型可靠性较高。本文方法采用10名受试者的数据全部作为训练，1 名受试者数据全部做测试，测试结果与专家人工标注结果的一致性较高，说明该方法泛化能力较强，具有一定的临床价值，为自动睡眠分期应用于临床提供了更广的思路。