面向高铁站的热舒适度和能耗综合预测
蒋阳升,王胜男,涂家祺,李 莎,王红军
(1.西南交通大学交通运输与物流学院,成都 611756;2.中铁二院工程集团有限责任公司建筑工程设计研究院,成都 610031;3.西南交通大学经济管理学院,成都 610031;4.西南交通大学信息科学与技术学院,成都 611756)
0 引言
高铁站是大量客流聚集的公共场所,其室内环境舒适程度对乘客候车过程中的身心健康和出行状态具有直接影响。为方便旅客进出,高铁站进出站口通常处于半封闭半开放状态,室内外能量交换频繁,使得高铁站室内环境舒适度受到诸多因素的影响。为了提高室内环境舒适度,通常高铁站配置有多联机及热交换机等空调系统,但由于高铁站楼层高、空间跨度大、空气流动性强以及围护结构多为玻璃建筑等特点,由此又带来巨大的能耗。高铁站作为城市中重要的空间节点,如何借助传感器技术、数据挖掘技术、机器学习算法等有效感知高铁站室内环境舒适度特征,获取影响高铁站室内环境舒适度和能耗的关键因素,并准确预测其变化规律,实现舒适的高铁站室内环境同时又达到节能降耗的目标是城市计算的新课题[1-2]。
基于此,本文以四川省某高铁站为研究对象,基于城市计算框架,以表征室内环境舒适度的指标——PMV(Predicted Mean Vote)、空调能耗综合值为目标,使用6 种机器学习模型进行综合预测。预测结果能够用于制定高铁站智慧温控系统的控制策略。
本文的主要研究贡献如下:
1)考虑到高铁站属于半封闭公共建筑空间、室内外热交换频繁、旅客集聚密度高等特点,针对性地提出影响高铁站室内环境热舒适度和能耗的8 个因素——室外温度、客流密度、多联机开启台数、多联机设置温度、热交换机开启台数、室内温度、室内湿度、室内二氧化碳浓度。
2)为了全面刻画高铁站的室内舒适度、能耗的变化规律,本文提出采用传感器数据捕捉及Energy Plus仿真两种方式对高铁站室内外状态、多联机及热交换机等控制单元及热能传导环境进行建模,并设计424 种运行工况以充分获取数据资源。
3)为了描述热舒适度及能耗与各影响因素的非线性关系,本文提出回归预测模型选择框架,通过内嵌6 种机器学习方法,并采用两个预测性能评价指标以及Friedman 统计量及Iman-Davenport 统计量选择最佳的高铁站室内热舒适度和能耗预测模型。该模型所获得的预测数据能够有助于温控系统主动预判环境状态参数,为下一阶段的温度控制策略制定提供准确实时的决策场景,避免传统温控系统所产生延时的控制策略而影响温控效果。
1 相关工作
1.1 热舒适度
20世纪70年代,Fanger[3]通过大量气候室实验研究,首次提出了PMV 指标。该指标综合了空气温度、湿度、流速、平均辐射温度、服装热阻以及人体新陈代谢率6 个因素,是迄今为止应用最广、最全面的热舒适度评价指标[4]。近年来,有不少国内外学者已经对热舒适度预测展开研究。主要研究成果可以分为热舒适度影响因素分析、基于机器学习方法的热舒适度预测两类。
1)热舒适度影响因素分析。该类研究侧重于研究环境因素对热舒适度的影响。Chow等[5]在香港进行了一项以实验室为基础的热舒适性调查,发现人的热舒适感对空气温度和速度很敏感,但对湿度不敏感。刘永颉等[6]利用PMV 方程对典型温带地区的热舒适度影响因素进行分析,最终确定空气温度和平均辐射温度是主要因素。Chan等[7]则通过建立人工神经网络模型来预测香港室外城市公园的热舒适性,研究表明,热感觉是影响热舒适评价的最重要因素,其次是夏季和冬季的气温。为了研究人的热历史是否会影响热舒适度,Jowkar等[8]选取了1 225名在英国居住不到3年的学生以消除在英国适应气候变化的影响进行实验,研究表明,有较温暖热历史的人的热偏好和舒适温度值高于普通人,为后续研究热舒适度影响因素提供了更好的参考。
2)基于机器学习方法的热舒适度预测。该类研究主要采用机器学习相关算法对热舒适度进行预测。高立新[9]和Yuce等[10]分别利用人工神经网络来建立智能预测器以及预测室内游泳池的能耗和热舒适度水平。侯赞等[11]将集成学习运用到了列车的热舒适度评价上,研究证明,集成学习能提高热舒适度评价的准确性。Marvuglia 等[12]提出了一种基于神经模糊联合模型的室内温度控制器,通过自回归神经网络进行室内温度预测,驱动模糊控制器,从而实现对办公大楼室内的温度控制。潘伟强等[13]和杨福迈[14]均利用支持向量机对室内热舒适度进行评价,前者将结果与反向传播(Back Propagation,BP)神经网络和概率神经网络比较,证明该方法的可行性,后者则提出了针对寒冷地区的热舒适度评价方法及评价规则,为该地区热舒适度的评价提供了依据。张玲等[15]和郭彤颖等[16]分别利用改进的粒子群算法和鸟群算法去优化BP 神经网络,并在此基础上提出了热舒适度预测模型,结果证明,改进后的模型比传统模型预测精度更高、收敛更快。Salamone等[17]在PMV 的基础上,增加PPD(Predicted Percentage of Dissatisfied)和用户反馈,作为个人热舒适的评价指标,并使用机器学习中的分类回归树(Classification And Regression Tree,CART)方法来预测用户的个人资料和热舒适感知对室内环境的影响。Guenther 等[18]则另辟蹊径,提出了一种基于高斯过程回归方法的个性化舒适预测模型。Ji等[19]通过对哈尔滨地区居民楼的实地考察和调查问卷,得出了住户的舒适度区间,并利用逻辑回归分析进行验证,给出了我国严寒地区舒适和节能的具体设置温度,为寒冷地区的节能控制提供了新的参考。Wang等[20]通过分析美国供暖、制冷和空调工程师协会(American Society of Heating,Refrigerating and Air-Conditioning Engineers Ⅱ,ASHRAE Ⅱ)数据,确定了居住者热体验的指标,并利用逻辑回归和支持向量机方法进行热可接受性和热偏好的预测。Mui 等[21]为了提高热舒适模型预测的精确度,提出了两种贝叶斯更新方法(全局更新和个体更新)用于改进现有的热舒适模型。Luo 等[22]对比了机器学习中用于预测热舒适参数的9 种方法,得出随机森林具有最高的预测准确性。Ngarambe 等[23]将人工智能方法运用到热舒适度的预测中,力求在不牺牲居住者热舒适性的情况下优化能源性能。
1.2 空调能耗预测
空调能耗预测一直是暖通空调的热门研究方向。目前学者对空调能耗预测方法主要分为传统预测方法和机器学习方法。
1)传统预测方法。Kikegawa 等[24]和Li 等[25]均考虑了城市热岛效应对夏季建筑空调能耗的可能影响,并建立了建筑物能源使用与城市气象条件之间的相互作用的多尺度模型。研究指出,估计的空调能源消耗远大于以往文献报道的空调能源消耗。杨世忠等[26]对空调冷却水系统进行节能研究,为空调节能提供了新的研究途径。Jim[27]和Yuan 等[28]则从建筑的屋顶设计和保温特性出发,分别在香港和上海两地展开建筑特性对空调能耗的实地调查,为炎热夏季城市的绿色屋顶和相关建筑保温的政策和设计提供了参考。Ma 等[29]则利用组合权重法选择相似天数对建筑物空调系统能耗进行预测,并采用eQUEST 仿真验证,结果表明,利用相似天数预测能耗具有较高的准确性。Zhou 等[30]在前人的基础上,通过分析北京、台湾、香港和伯克利四个地点在气候、围护结构、居住者行为上的差异以及办公楼的空调能源使用情况,得出了居住者行为影响最大的结论。
2)机器学习方法。为了提高空调能耗预测的准确性,研究者将机器学习应用到了空调的能耗预测上。Atthajariyakul等[31-32]将PMV、二氧化碳浓度和冷热负荷分别作为热舒适、室内空气质量和能耗的参数指标,提出了一种基于神经网络的PMV 模型用于确定暖通空调系统最佳室内空气状态。实验结果表明,与传统方法相比,该方法可以有效地实现暖通空调系统室内空气状态的实时监测,同时降低能耗。Wei 等[33]提出了一种数据驱动的方法来优化典型办公设施中暖通空调(供暖、通风和空调)系统的总能耗,并建立了一种综合设施温度、相对湿度、二氧化碳浓度的总能量模型,利用改进的多目标粒子群算法对模型做进一步优化,在节能方面取得显著进展。Zheng 等[34]提出了一种改进的入侵杂草优化算法,以解决使功耗最小化的冷水机组负荷问题,与其他算法相比,该算法可以找到相等或更好的最优解。段冠囡等[35]提出了一种基于GM-RBF(Grey Model-Radical Basis Function)的神经网络方法对超高层建筑的空调能耗进行预测,并达到较高的预测精度。钱青等[36]则将总能耗分项,利用自回归和深度置信网络(Auto-Regression-Deep Belief Network,AR-DBN)建立能耗短期预测模型,与不分项模型相比,该模型预测精度较高。Tran等[37]利用最小二乘支持向量回归和径向基函数神经网络两种机器学习方法,构建了进化神经机器推理模型。该模型比其他人工智能技术具有更高的预测精度。魏峥等[38]讨论了使用机器学习的方法对冷水机组进行控制以降低能耗,优化运行的情况,得出支持向量机(较差)、神经网络、随机森林三种算法都有较好的适用性的结论。Zhou 等[39]利用长短期记忆模型预测广州某高校图书馆的空调系统。结果表明,长短期记忆模型能够产生更可靠的预测结果。综上,当前对热舒适性以及空调能耗的研究有比较丰富的研究成果,但还存在以下不足:
1)大多文献主要考虑封闭空间的热舒适度,而高铁站是一类典型的半封闭半开放的建筑空间,承担大量客流集散任务,同时室内室外热交换频繁,热舒适会受到室内室外诸多因素的影响,需要针对高铁站的特点,提炼其室内热舒适度的影响因素。
2)大多文献采用某种机器学习算法对热舒适度或者能耗进行预测。而对于高铁站而言,由于其半开放的建筑空间特点,各类因素的影响路径复杂,需要设计多个机器学习算法以确定最佳的预测性能。
3)大多文献没有将热舒适度和能耗结合起来共同预测。由于热舒适度和能耗存在背反关系,即追求高舒适度会导致高的能耗,如何同时预测两个目标并协调两者关系仍待解决。
基于此,本文以四川省某高铁站为研究对象,提炼了影响其室内舒适度及能耗的多个因素,并建立了热工环境模型,同时将双目标(PMV 和能耗)转化为单目标,并采用了6 种机器学习方法对两者进行综合预测。通过大量实验对比6 种机器学习方法在实验数据集上的测试效果,最终选出最优预测模型。
2 问题描述
通过大量的文献调研及实地走访,本文最终确定影响高铁站室内舒适度和能耗的因素分别为:多联机开启台数、多联机设置温度、热交换机开启台数、客流密度、室外温度、室内温度、室内湿度、室内二氧化碳浓度。高铁站室内热舒适度评价选用目前广泛应用的PMV 指标。为了获取各影响因素与PMV 和能耗之间的复杂非线性关系,本文首先基于现场安装传感器进行数据捕捉,然后基于Energy Plus 构建高铁站的热工环境模型,并使用传感器数据对模型进行校正与多轮调试,保证所构建的模型能够复现高铁站真实的热工环境。根据各影响因素的作用范围,设计不同工况以获取海量数据,并计算PMV 与能耗值。最后通过6种预测方法(线性回归、深度神经网络、岭回归、支持向量回归、贝叶斯岭回归、决策树回归)进行综合预测。
2.1 PMV定义
PMV 代表了大多数人在同一环境中的平均冷热感觉,它根据人体产热和散热之间的差值进行计算,该值一般与用户在房间中的运动和服装情况及环境情况有关。本文的PMV值采用计算值,具体计算公式如下式(1)[40]所示:

其中:M表示人体能量代谢率,单位为W/s;W表示人体所做的机械功,单位为W/s;Pa表示人体周围空气的水蒸气分压力,单位为Pa;ta表示人体周围的空气温度,单位为℃;ts表示房间的平均辐射温度,单位为℃;fcl表示人体着装后的实际表面积和人体裸身表面积之比,即服装的表面系数;tcl表示人体外表面温度,单位为℃;hc表示对流换热系数,单位为W/s·m2·℃;
本文中将根据所构建的热工环境中各时刻的状态参数,如人体周围的空气温度等,依据式(1)对该时刻的PMV 进行计算。
2.2 预测目标函数的建立
为了同时预测PMV 和能耗,并减少预测复杂度,本文将这两个目标通过线性加权的方式转化为单目标。根据文献[41],本文PMV权重取值为0.6,能耗项权重取值为0.4,以求得热舒适性和能耗的综合值为最优。
由于两个目标的取值与量纲存在较大的差异,为了减少误差,需要对其进行标准化处理。此外,考虑到PMV 的取值范围,对其进行绝对值处理。处理之后的预测目标如式(2)所示。
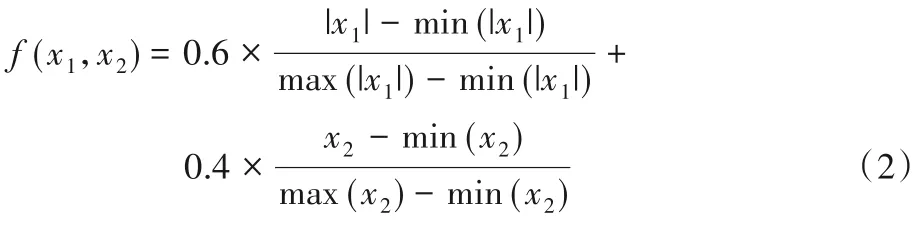
其中:f(x1,x2)为预测目标值;x1为PMV 值;x2为能耗值,为开启的多联机和热回收机的能耗总和;max(|x1|)、min(|x1|)为PMV 值中的最大、最小值;max(|x2|)、min(|x2|)为总能耗中的最大、最小值。
3 高铁车站热工环境建模
3.1 高铁车站调研概况
本次调研选取处于夏热冬冷地区的四川省某高铁站为研究对象,该车站为高架车站,站厅层高6 m,吊顶1 m,可大致分为办公区、候车区、离站区3 个区域,其中候车区的尺寸为74 m×28 m×5 m。该车站共配有5台多联机和8台热交换机。
本次调研时间为2019年12月31日—2020年1月3日,调研的内容包括高铁站室内外环境因素的现场实时测试(包含温度传感器、湿度传感器、二氧化碳传感器的安装与数据捕捉)、客流密度的实时统计以及站内候车乘客的问卷调查。问卷调查时间间隔为半小时。
3.2 建模数据收集
为了获得海量数据,本文基于Energy Plus 软件建立高铁车站的热工环境模型,模拟了高铁车站全年的热交换与空调能耗情况。该高铁车站位于四川(北纬30.61°,东经103.68°),建筑朝向为北偏东30°。根据高铁车站平面图在sketch up 中建立一个长81.8 m、宽74 m、高5 m 的三维模型;模型中围护结构构造、建筑结构等参数均严格按照该高铁站实际数据进行设置,各结构布置完成后match 最终模型,从而进行内外墙的识别,确认模型无误以后,生成IDF 文件,导入EP-Launch进行参数设置及能耗模拟。数据模拟从1月1日开始,12月31日结束,模拟的时间段为7:00—23:00。与此同时根据实地调研结果,对所建模型进行校正与调试。就控制系统开行状态,本文设计了5+8+40=53种工况,分别为单独开多联机、单独开热交换机以及多联机和热交换机的组合。与此同时,通过文献调研与实地访谈,设置了8 种多联机夏季温度与冬季温度组合,具体情况如表1。生成了53×8=424种工况,因此,共获取424×8 760=3 714 240个实例。

表1 多联机温度组合Tab.1 Temperature combination of multi-evaporator air conditioners
4 高铁站热舒适度和能耗综合值预测模型
4.1 回归预测模型的理论
高铁站热舒适度与能耗综合预测是一类回归问题,因此本文选取深度神经网络、支持向量回归、决策树回归、线性回归、岭回归、贝叶斯岭回归共6 种机器学习方法,建立以PMV和空调能耗综合值为目标的回归预测模型,根据回归预测模型选择框架最终确定最佳的模型。各模型简述如下。
1)深度神经网络(Deep Neural Network,DNN),也称为多层感知机。在2006 年,Hinton 等[42]利用预训练方法缓解了局部最优解问题,将隐藏层推动到了7 层,深度神经网络由此出现。近年来,很多学者也将其应用到回归问题上。神经网络中,设置激活函数是σ(z),隐藏层和输出层的输出值为a,第l-1 层共有m个神经元,则对于第l层的第j个神经元的输出得到式(3):
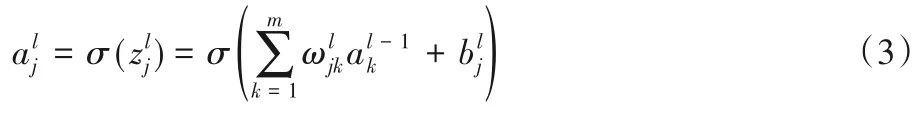
2)支持向量回归(Support Vector Regression,SVR)。1998年,Haykin[43]将支持向量(Support Vector,SV)学习正式纳入机器学习标准方法工具箱,在2002 年Smola[44]对支持向量回归有了更深入的概述。SVR 作为支持向量机的延伸,设容忍f(x)与y之间有ε的偏差,则SVR问题可以写为式(4):

其中:C为惩罚因子,ℓε为不敏感损失函数。
3)线性回归(Linear Regression,LR)[45]。设预测值为则LR问题可以写为式(5):

其中:ω=(ω1,ω2,…,ωp),xi=(xi1,xi2,…,xip)。
4)岭回归(Ridge Regression,RR)[46]。通过对系数的大小进行惩罚来解决普通最小二乘问题,其函数可以表示为式(6):

其中复杂性参数α≥0 控制收缩量:α的值越大,收缩量就越大,因此共线性系数也更大。
5)贝叶斯岭回归(Bayesian Ridge Regression,BRR)[47],具体模型表示为式(7):

其中:α1、α2、λ1和λ2分别是关于α和λ的γ分布的先验。
6)决策树回归(Decision Tree Regression,DTR)[48]是一种可以用于回归的决策树模型,通过非参数分类和回归方法进行有效的预测。假设X和Y分别为输入和输出变量,给定训练数据集为D={(x1,y1),(x2,y2),…,(xN,yN}) 其中xi=为输入实例(特征向量),n为特征个数,i=1,2,…,N,N为样本数量。
对特征空间的划分采用启发式方法,每次划分逐一考察当前集合中所有特征的所有取值,根据平方误差最小化准则选择其中最优的一个作为切分点。如对训练集中第j个特征变量x(j)和它的取值s,作为切分变量和切分点,并定义区域R1(j,s)={x|x(j) ≤s}和R2(j,s)={x|x(j) >s},为找出最优的j和s,求解式为式(8):

找出使要划分的两个区域平方误差和最小的j和s。其中,c1、c2为划分后两个区域内固定的输出值,方括号内的两个min 意为使用的是最优的c1和c2,也就是使各自区域内平方误差最小的c1和c2,易知这两个最优的输出值就是各自对应区域内y的均值,所以式(8)可写为式(9):
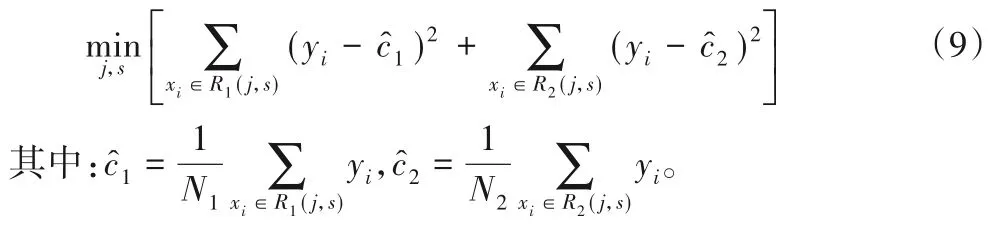
找到最优的切分点(j,s)后,依次将输入空间划分为两个区域,接着对每个区域重复上述划分过程,直到满足停止条件为止。这样就生成了一棵决策回归树。本研究通过对比6 种机器学习方法对仿真数据预测的准确性,最终选出适合于本研究的最优回归预测模型。
4.2 热舒适度和能耗综合预测模型选择框架
为了选择合适的模型对高铁站室内热舒适度和能耗进行准确预测,本文设计了回归预测模型选择框架,具体过程如图1所示。

图1 回归预测模型选择框架Fig.1 Selection framework of regression prediction model
5 实验与结果
5.1 数据预处理
将数据集输入模型进行训练前,需要对其进行预处理,具体步骤包括:
步骤1 数据划分。按月份将数据分为12组。
步骤2 缺失值与异常值的处理。删除数据集中缺失能耗的数据及异常值。
数据预处理后的数据集如表2所示。

表2 实验数据集的样本、特征、问题属性数量Tab.2 Numbers of instances,features and problem properties of experimental datasets
表2 中的问题属性即为本研究的目标函数,包括PMV 值和总能耗值两种属性。
5.2 评价指标
本文选取均方误差(Mean Squared Error,MSE)[49]和拟合优度(RSquared,R2)[50]两个指标来评价模型预测性能。
MSE标准计算如式(10)所示:

其中:n为测试样本的数量,yi表示PMV 和能耗综合值的实际值表示回归模型的预测值。MSE的值越小,代表预测的准确率越高。
R2标准计算如式(11)所示:

为了进一步测试算法准确性,本文使用十折交叉验证对6 种算法进行测试,即将数据集分成10 份,依次将其中9 份作为训练数据,1份作为测试数据,进行实验。将10次结果的正确率(或差错率)的平均值作为对算法精度的估计。
为了检验不同算法的差异,本文使用Friedman统计量,其定义如下:


5.3 实验参数设置
本研究的部分模型依赖超参数的选择,为了保证实验的严谨性,在测试模型的过程中,根据超参数不同设置对模型进行调参优化操作。因线性回归不需调参,本研究对其他5 个模型的超参数进行调试优化,具体过程如下。
针对岭回归中的超参数α,首先设置取值范围为[0,1 000],步长为100进行调参。实验表明当α取值为100,MSE的值达到最小0.005 6。随之将α取值范围调至[50,150],步长为10;取值范围为[80,100],步长为2以及取值范围为[85,95],步长为1 进行参数微调。最终确定当α=90 时MSE的值最小。
对于支持向量机回归,本实验主要调节惩罚系数C的设置。设置C的取值范围为[0.5,1.5],步长为0.1 进行实验。结果表明当C=1.1时,MSE的值达到最优,为0.012 7。
决策树回归主要通过min_samples_split参数来控制叶节点上的样本数量。设置min_samples_split的取值范围为[2,15],步长为1进行参数测试。结果表明,当min_samples_split=11时,MSE最优,为0.002 0。
贝叶斯岭回归主要调节超参数α1、α2,它们是α关于γ分布的先验,默认α1=α2=10-6。本研究测试了α1、α2分别取值10-7、10-6、10-5下的9 种组合,最终测试结果表明α1、α2的变化对MSE值不产生影响。
深度神经网络的效果主要依赖网络层数的选择,本研究测试了1)8→16→18→12→1;2)8→24→12→1;3)9→16→18→24→12→1 三种不同层数、不同神经元个数的网络结构,最终测试结果显示第1)种优于其后两者,MSE为0.011 3,故选择1)结构构建模型。
5.4 实验与结果
本文所选取的6 种机器学习算法,其MSE和R2结果以及测试时间如图2~4及表3~5所示。

图2 MSE标准的十折交叉验证结果对比Fig.2 comparison on MSE

图3 R2标准的十折交叉验证结果对比Fig.3 Ten-fold cross-validation result comparison on R2

图4 十折交叉验证结果的实验时间对比Fig.4 Ten-fold cross-validation result comparison on experimental time
由图2~4可知,不论是在MSE标准的十折交叉验证下,还是在R2标准的十折交叉验证下,6 种算法中,DTR 的预测性能最佳。由表3~5 可知,6 种回归模型中,DTR 的综合预测性能最佳。在MSE方面,12 个数据集中有11 个DTR 都取得了最小值。在所有的数据集中,DTR的平均MSE最低,为0.002 2。其余算法的平均MSE从小到大依次为0.005 6(LR),0.005 6(RR),0.005 6(BRR),0.016 1(SVR),0.025 2(DNN)。在R2方面,12个数据集中有10个数据集DTR都取得了最大值。在所有的数据集中,DTR 的平均R2最大,为0.793 8。在第5 个数据集达到了最大R2(0.937 2)。其余算法的平均R2从大到小依次为 0.431 6(RR),0.431 1(BRR),0.431 0(LR),-0.159 0(DNN),-0.789 8(SVR)。在运行时间方面,DTR 的平均运行时间0.175 0 s,也大大优于DNN(3.166 7 s)。

表3 6种机器学习算法的均方误差及秩次Tab.3 Mean square error and rank for six machine learning methods
为了检验6 种机器学习算法的总体性能,本文使用Friedman 统计量进行假设检验。6 种算法在各个数据集上MSE的平均秩次分别为5.750 0,5.250 0,2.916 7,2.916 7,2.916 7,1.250 0。MSE的Friedman统计量为:

6 种算法在各个数据集上R2的平均秩次分别为5.583 3,5.416 7,3.166 7,2.916 7,2.416 7,1.500 0。R2的Friedman 统计量为:

本次对比实验基于6个算法,12个数据集,FF服从于自由度为6-1=5 和(12-1)(6-1)=55 的F 分布。由F(5,55)分布计算FFMSE、FFR2所对应的p的值分别为9.486 26E-19、7.205 94E-17,所以在高显著性水平下拒绝原假设,综合图2~4结果可知DTR 算法在高铁站热舒适度和能耗预测的准确率均优于其他对比算法。

表4 6种机器学习算法的拟合优度及秩次Tab.4 R2 and rank for six machine learning methods

表5 均方误差及R2的实验时长比较 单位:sTab.5 Comparison of experimental time for MSE and R2 unit:s
6 结语
对于高铁站热舒适度和能耗的预测研究,对实现高铁站智能温控,改善人们的生活环境和节能减耗具有重要意义。
本文通过现场传感器数据捕捉及Energy Plus平台对四川省某高铁候车厅室内外状态、多联机及热交换机等控制单元及热能传导环境进行建模,获取影响高铁站室内热舒适度和能耗的8 个因素:室外温度、客流密度、多联机开启台数、多联机设置温度、热交换机开启台数、室内温度、室内湿度、室内二氧化碳浓度。通过传感器数据对所建热工模型进行校正与调试,并运行424种工况,生成3 714 240个实例。为了获取热舒适度及能耗的变化规律,本文基于回归预测模型选择框架,运用6 种机器学习方法(深度神经网络、支持向量回归、决策树回归、线性回归、岭回归、贝叶斯岭回归)对高铁站室内热舒适度及能耗进行综合预测。通过大量实验可知,6 种机器学习算法中,决策树回归模型预测能够在较短的时间内获得最佳的预测性能。相比其他算法,决策树回归模型在所有的数据集里,其平均R2最大,为0.793 8,平均MSE最低,为0.002 2。综上,决策树回归能够较好地反映高铁站室内热舒适度和能耗的变化规律,可以为室内环境的智慧温控系统的控制和节能减耗提供决策支持。

