带有自适应合并策略和导向算子的增强型烟花算法

李克文，马祥博*，候文艳

（1.中国石油大学（华东）计算机科学与技术学院，山东青岛 266580；2.中国石油大学（华东）海洋与空间信息学院，山东青岛 266580）

0 引言

在中国的传统文化中，每逢新年人们通常都会燃放大量的烟花来庆祝，众所周知，好的烟花爆炸时能产生数量较多，均匀分布和五彩斑斓的火花；相反差的烟花只能产生图形单一且数量较少的火花。烟花算法（FireWorks Algorithm，FWA）［1］是由北京大学谭营教授2010 年提出的，是一种模拟烟花爆炸并结合进化计算的随机搜索而提出的群智能算法。相较于其他群智能算法，烟花算法具有明显的自身特点如多样性、爆炸性等。自烟花算法被提出以来，已经吸引了许多学者的研究，相关改进算法不断被提出，从而使得烟花算法开始广泛应用于各个领域。但是到目前为止烟花算法仍有一些不足有待改进，例如寻优过程中粒子间缺少有效交互［2-5］以及爆炸半径对搜索范围的限制［6-9］等。

本文针对以上提到的两个问题进行深入研究，主要贡献如下：

1）本文提出了一种带有自适应合并策略和导向算子的增强型烟花算法（Enhanced FireWork Algorithm with adaptive Merging strategy and Guidance operator，EFWA-GM），相较于传统烟花算法能够提高算法的寻优精度和收敛速度；

2）在迭代过程中，利用切比雪夫距离度量烟花粒子爆炸范围之间的位置关系，对寻优空间中重叠的爆炸范围进行自适应合并，提高算法的寻优精度；

3）通过将火花粒子划分为4 个等级，充分利用优质粒子的位置信息，引入导向算子引导次优粒子进化，提高算法的收敛速度；

4）应用不同标准测试函数的实验结果表明本文提出的带有自适应合并策略和导向算子的增强型烟花算法相较于传统烟花算法，在寻优精度和寻优速度方面有更好的优化性能。

1 相关工作

自2010 年，Tan 等［1］基于烟花的爆炸结合进化计算的随机搜索提出了烟花算法，该算法由于具有较强的优化问题求解能力受到研究者的广泛关注。此后，许多改进算法相继被提出，该算法便广泛应用于各个领域。目前，对烟花算法的改进仍存在一些问题有待解决，如寻优过程中粒子间缺少有效交互以及爆炸半径对搜索范围的限制。

Liu 等［2］针对烟花算法进行了改进，提出了一种新颖的爆炸火花数量和爆炸幅度的计算方式，设计了一种传递函数将烟花的等级传递到火花数量和爆炸幅度的计算上，并采用一种新颖的随机变异算子来增加烟花算法的多样性。Pei 等［3］利用精英选择策略研究了近似算法对提高烟花算法收敛速度的影响，并通过实验验证了可以有效提高烟花算法的收敛能力。Zheng 等［4］详细地分析了不同自适应烟花算法的改进策略以及效果，并对自适应烟花算法的常见改进策略进行了分析。Yu 等［5］首先分析了不同改进烟花算法的性能，然后提出了动态搜索烟花算法，引入了指数递减的爆炸范围计算策略从而增强其局部搜索能力。Zheng 等［6］对烟花算法的算子进行了详细的分析，针对烟花算法的缺点进行了相应的改进，包括爆炸半径的大小、爆炸火花的产生方式、变异算子、映射规则和选择策略，提出了增强型烟花算法（Enhanced FireWorks Algorithm，EFWA）。Yu 等［7］提出了动态搜索烟花算法（dynamic FireWorks Algorithm，dynFWA），在dynFWA 中将烟花种群分为核心烟花（适应度值最优的粒子）和非核心烟花，核心烟花的爆炸半径根据动态搜索策略进行自适应调整，并且去掉了高斯变异算子使dynFWA 的时间消耗相对较小。Li等［8］提出了自适应烟花算法（Adaptive FireWorks Algorithm，AFWA），将爆炸火花中的最差个体与最优个体之间的距离作为下一次迭代的爆炸半径，在初始阶段能够根据局部区域的大小进行调整，在最后的微调阶段能够使爆炸半径逐渐减小从而找到极值点，因此AFWA 表现出了较好的寻优性能。Li等［9］在烟花算法中引入了一种导向算子（guided sparks），提出了有导烟花算法（Guided FireWorks Algorithm，GFWA）。

以上改进方法相对传统烟花算法性能有了较大的提升，但都没能很好地解决上述两个问题。本文提出一种带有自适应合并策略和导向算子的增强型烟花算法，利用自适应合并策略，降低爆炸过程中的半径限制，并通过导向算子利用优质粒子的位置信息引导次优粒子进化，提高优化能力。通过12个标准的测试函数检验了算法的有效性和鲁棒性。

2 增强型烟花算法

烟花算法模拟夜空中烟花爆炸的现象，通过初始化N个烟花粒子，经过爆炸和变异生成新的火花，并基于欧氏距离从烟花粒子、火花粒子和高斯变异粒子选择新一代的N个烟花粒子，开始迭代直到满足问题的精度或者达到最大函数评估次数。

增强型烟花算法（EFWA）由Zheng等［6］于2013年提出，针对FWA 的缺陷对各个算子进行了改进，从而提高了算法的寻优能力，本文提出的带有自适应合并策略和导向算子的增强型烟花算法（EFWA-GM）基于EFWA提出。

2.1 小爆炸半径检测

EFWA 中引入最小爆炸半径检测机制，如果烟花粒子的爆炸半径小于某一阈值，则将其设置为默认值，如式（1）：

对于如何确定Amin，k，EFWA 提出了非线性递减策略，如式（2）：

其中：Ainit和Afinal表示迭代过程中的最初和最终的爆炸半径阈值，t表示当前函数的评估次数，evaltimes表示最大函数评估次数。

2.2 爆炸火花产生方式

FWA 中烟花爆炸产生火花时在所有维度上的权重是相同的，但是不同维度上相同的权重会降低火花的多样性，因此EFWA 在每个维度上使用不同的权重值。此外，在FWA 中当一个爆炸或者高斯变异产生的火花在维度k上超出边界，会通过式（3）的映射规则将花火映射到边界内区域，即FWA 中烟花爆炸产生火花时在所有维度上的权重是相同的，但是不同维度上相同的权重会降低火花的多样性，因此EFWA 在每个维度上使用不同的权重值。此外，在FWA 中当一个爆炸或者高斯变异产生的火花在维度k上超出边界，会通过式（3）的映射规则将花火映射到边界内区域，即：

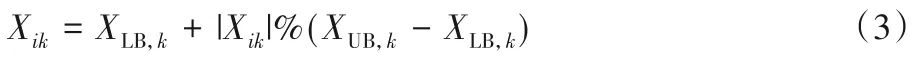
其中：XLB，k、XUB，k为解空间在维度k上的下边界和上边界。在这种情况下，在维度k上超出边界的火花会被映射到距离原点较近的位置。为了解决这一问题，EFWA 使用式（4）来处理超出边界的火花：

其中：XUB，k、XLB，k为可行域在维度k的上边界和下边界，U（0，1）表示在区间（0，1）的均匀分布。

2.3 高斯变异算子

为避免FWA 中高斯变异花火的缺陷，在EFWA 中使用一种新型高斯变异算子，计算公式为：

其中：XBk表示当前种群中适应度值最优的烟花粒子的第k个维度，g～N（0，1）。

3 带有自适应合并策略和导向算子的增强型烟花算法

当烟花粒子爆炸产生火花时，火花粒子的位置及适应度值包含了大量的寻优信息［10］，但是传统的烟花算法并没有充分利用这些信息来指导烟花粒子的寻优过程，同时烟花粒子的爆炸半径限制了火花粒子的搜索范围，导致收敛速度变慢、寻优精度降低。本文针对这两个问题提出了带有自适应合并策略和导向算子的增强型烟花算法。

3.1 自适应合并策略

传统烟花算法特殊的爆炸机制将火花粒子的搜索范围限制在烟花粒子的爆炸半径之内，若两个烟花粒子的距离较近，烟火粒子的爆炸范围很可能相交，如图1（a）所示。本文中认为，经过烟花粒子的多轮爆炸和重新选择，两个烟花粒子爆炸范围相交能够表明当前决策区域较大可能存在优质解［11-12］。那么，当前迭代轮次，区域A 作为相交区域的邻近区域，应当具有与区域B、C 相同的概率产生优质解，即区域A、B、C 获得搜索的地位是相同的，同时本文实验结果也证明对相交区域的邻近区域的搜索是高回报的，但是传统烟花算法中区域A、B、C 的获得搜索的地位是不相等，这导致优化精度和收敛速度的降低。针对此问题，本文提出了自适应合并策略，当烟花粒子的爆炸边界相交时，通过合并烟火粒子的爆炸范围来使区域A、B、C 获得相同的搜索地位，以提高算法的优化性能，如图1（b）所示。通过自适应合并策略，烟火粒子在新的爆炸范围以相同的概率产生火花粒子，如图1（c）所示。

图1 自适应合并策略示意图Fig.1 Schematic diagram of adaptive merging strategy

考虑烟花粒子间的距离，本文认为当烟花粒子的所有维度距离都较近时，才认为两个烟花粒子距离相近或相交，这样能够避免不必要的爆炸范围合并，提高算法的收敛速度，因此本文中选择切比雪夫距离［13］作为自适应合并策略的距离度量，计算公式如下：

其中：Di，j表示烟火粒子i和j的切比雪夫距离，Xi、Xj表示烟火粒子i、j的位置。

自适应合并策略通过重新计算烟花粒子的爆炸范围，在新的爆炸范围内产生火花粒子进行搜索，如式（7）～（8）所示：

其中：Ai、Aj分别表示烟花粒子i、j的爆炸范围，Amax表示最大爆炸范围表示新确定的爆炸范围。

自适应合并策略具体的实现方法如算法1所示。

算法1 自适应合并策略。

3.2 导向算子

在增强型烟花算法中，由于寻优过程中烟花粒子间缺少有效的信息交互，限制了普通粒子的搜索能力。本文提出一种利用导向算子来缓解这一问题，将适应度值最优的三个粒子分别定义为L1、L2和L3，通过L1、L2、L3指导其他次优粒子向着目标最优解搜索，其余的粒子被定义为L4，它们围绕着L1、L2或L3更新自己的位置。火花粒子的等级如图2所示。

图2 火花粒子的等级Fig.2 Levels of spark particles

在优化问题的决策空间中，对最优解的位置并不了解，因此适应度值较优的L1、L2 和L3 粒子更了解最优解的潜在位置［9］。本文通过引入一个导向算子，利用优质烟花粒子的位置来预测目标最优解的潜在位置，同时引导次优粒子更新其位置逐渐逼近目标最优解。导向算子引导烟花粒子更新位置的示意图如图3所示。

图3 导向算子引导烟花粒子更新位置的机制Fig.3 Mechanism of guidance operator guiding fireworks particles to update their positions

如图3中，L4等级的火花粒子基于与L1、L2、L3等级粒子之间的距离向量DL1、DL2、DL3，计算L4 等级粒子的位置更新方向和步长，L′4表示位置更新后的粒子，距离向量DL1、DL2和DL3的计算公式如式（9）所示：

其中，DL1、DL2和DL3分别表示L1、L2 和L3 烟花粒子与其他粒子间的距离，XL1、XL2、XL3分别表示L1、L2和L3烟花粒子的当前位置，X表示当前粒子的位置，C1、C2、C3是随机向量。

式（10）分别定义了烟花种群中L4 等级的个体向高等级的L1、L2和L3前进的步长和方向，式（11）定义了L4个体经导向算子调整后的最终位置，其中A和C是系数向量，A和C的计算公式如下：

其中：a是收敛因子，随着函数评估次数从2 线性递减到0，r1和r2取［0，1］区间的随机数。

3.3 随机变异算子

由于EFWA采用的高斯变异算子是在当前粒子位置和坐标原点之间产生变异火花，容易将火花变异到原点附近的位置，导致EFWA算法易于求解原点附近的最优值，而对于远离原点的最优值则表现出较差的优化性能，故将高斯变异算子改为随机变异，公式如下

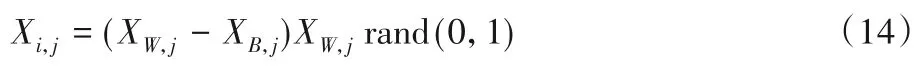
其中：XB，j、XW，j分别表示当前烟花种群中适应度值最低、最高的烟花在第j维度上的位置，Xi，j表示第i个粒子在第j维度上的位置，rand（0，1）表示在区间［0，1］区间均匀分布的随机数。

3.4 EFWA-GM流程

算法2 EFWA-GM。

步骤1 对N、FWmax、dim、a、b、Amax、maxEva等参数进行初始化，N为初始烟花个数，FWmax为种群中最大粒子数量，dim为测试函数的维度，a、b为给定的常数用来限制爆炸火花的数量和范围，Amax为最大爆炸范围的阈值、maxEva为最大函数评估次数；

步骤2 根据EFWA 中爆炸火花的范围和数量计算公式计算t=1时每个烟花的爆炸半径和火花数量；

步骤3 根据式（6）～（8）对烟花粒子的爆炸范围进行合并，并按照式（4）结合新的爆炸范围产生火花粒子；

步骤4 根据式（9）～（13）计算导向算子并引导L4等级粒子进行位置更新；

步骤5 根据式（14）产生变异火花，并由EFWA 的选择策略选择下一代烟花种群；

步骤6 循环步骤2～步骤5，直到达到最大函数评估次数或最小误差。

采用自适应合并策略，EFWA-GM 一定程度上能够缓解随机搜索受限于爆炸半径的问题，提高算法的收敛速度；引入导向算子，能够增强烟花粒子间的信息交互，提高种群的全局搜索能力；采用随机搜索算子能够提高最优值远离原点的测试函数的优化性能。

4 实验分析

4.1 小爆炸半径检测

为检验本文提出的EFWA-GM 在寻优精度、收敛速度方面的性能，选择12 个标准测试函数进行测试分析，比较EFWA-GM、标准粒子群优化（Standard Particle Swarm Optimization，SPSO）算法、增强型烟花算法以及较先进的自适应烟花算法、动态自适应烟花算法、导向烟花算法的优化性能，表1给出了标准测试函数表达式、最优值、搜索维度。

表1 标准测试函数Tab.1 Benchmark functions

本文实验平台是Python3.6.7（Centos7；Intel Core i5-8300H CPU 2.3 GHz；16 GB RAM）。对于每一个测试函数，EFWA 参数的设定参考文献［8］，具体如下：初始烟花数目N=5，高斯变异烟花数目p=5，最大种群数目FWmax=50，a=0.04，b=0.8，最大爆炸幅度Amax=40；EFWA-GM 和EFWA 参数设定相同；AFWA 参数的设定参考文献［10］，其中最大种群数目FWmax=100，最大爆炸幅度Amax=100，参数λ=1.3，其余参数设置与EFWA 相同；文献［14］和文献［15］出了SPSO 的实验结果。实验中EFWA、AFWA和EFWA-GM设置最大函数评估次数为300 000，PSO 设置最大迭代次数为2 000，每个测试函数独立运行30次。

4.2 实验结果

4.2.1 搜索精度分析

表2 列出了EFWA-GM、SPSO、EFWA、AFWA、dynFWA、GFWA 在12 个标准测试函数上的实验结果，并统计了6 种算法在12 个测试函数上的均值和方差，加粗数据为最优值。由表2 中数据可以得知：SPSO 的搜索精度最差且鲁棒性较低，AFWA 在Schwefel、Zakharov 两个测试函数上搜索精度取得最优，dynFWA 和GFWA 在Sphere 测试函数上取得最优，EFWAGM 在其余9个测试函数上取的最优值；并且不同维度的测试函数结果可见EFWA-GM 的表现也要优于其余算法。综合可得EFWA-GM 在极值函数的寻优精度方面要优于其他的5 种算法；而且，根据方差也可以发现，EFWA-GM 比其他3种算法表现更加稳定。

表2 实验结果对比Tab.2 Comparison of experimental results

4.2.2 收敛速度分析

为了比较EFWA-GM、EFWA和AFWA在收敛速度方面的表现，本文针对表1中的12个标准测试函数，以函数评估次数为横轴，以最优适应度值作为纵轴来描述算法的优化轨迹。如图4 所示，EFWA-GM 在Sphere、Rastrigrin、Griewank、Cigar、Ellipse、Ackley 测试函数上收敛速度明显优于EFWA 和AFWA，在其余6 个测试函数上收敛速度基本持平，由此可见EFWA-GM 的收敛速度要优于EFWA 和AFWA。这表明EFWA-GM 在收敛速度上比EFWA 和AFWA 有所加强，更加有利于解决复杂的优化问题。

图4 标准测试函数的进化曲线Fig.4 Evolution curves of benchmark functions

由此可见，EFWA-GM 无论在寻优精度还是在收敛速度方面均有较优的表现。这样的结果主要得益于两方面：一方面引入导向算子增加了烟花粒子间的有效交互，提高了粒子的搜索能力；另一方面采用自适应半径搜索策略，一定程度上降低了爆炸半径对搜索范围的限制，提高了算法的收敛速度，此外采用随机变异算子替代高斯变异解决了对最优值远离原点的测试函数表现较差的问题。

5 结语

本文针对增强型烟花算法粒子间缺少有效交互以及在搜索过程中受爆炸半径影响限制搜索范围的问题，提出一种带有自适应合并策略和导向算子的增强型烟花算法。该算法采用自适应合并策略，根据烟花粒子间距离对爆炸范围进行自适应合并，从而保证对相交区域邻近区域均等的搜索，提高算法的收敛速度；通过引入导向算子，将烟花种群划分为4 个等级，利用优质粒子的位置信息引导次优粒子向全局最优解靠近，提高算法的优化性能。实验表明本文提出的EFWA-GM在寻优精度和收敛速度方面均有较好的表现。