保证变形能力的钢筋混凝土低矮剪力墙抗剪承载力计算*

刘建 陈晓磊

(中冶建工集团有限公司 重庆400080)

引言

近年来低矮剪力墙(高宽比＜2.0)因其良好的经济性及较高的水平抗剪承载能力被广泛应用于层数较低的经济适用房、传统民用建筑以及与安全息息相关的核工业设施建筑结构当中。自20世纪五十年代, 许多研究者已对低矮剪力墙的剪切行为进行了研究并提出了多种抗剪承载力计算公式用于结构设计规范当中[1-10]。随后又进行了优化、改进。1990年Woods 等人对ACI 规范剪力墙抗剪承载力计算式进行评估, 并予以改进。Alcocer 等人[11]通过对各影响因素开展研究, 提出了新的抗剪承载力计算模型。Gulec 等人[12-14]应用367个低矮剪力墙试验结果对常用的5个抗剪承载力计算式进行评估, 表明Woods 的公式能较为准确地预测矩形截面低矮剪力墙抗剪承载力, 而工形及带端柱截面的剪力墙采用ASCE/SEI 43-05 规范公式计算更为有效。然而结构及其构件在大震作用下将进入塑性阶段, 不确定性因素将随之增加, 从而为构件承载力的准确预测带来极大的困难, 为确保剪力墙在地震作用下的安全性有必要从计算误差(考虑一定的安全性,即实际值高于计算值)及保证墙肢变形能力两方面对当前规范中低矮剪力墙抗剪承载力计算公式进行性能评估, 并依评估结果对公式进行改进。

本文对301个低矮剪力墙试验数据进行筛选并利用其试验结果对规范中应用较为广泛的五组抗剪承载力计算公式进行性能评估。试验数据中剪力墙的截面形式包括矩形截面、带端柱截面及翼缘截面三种截面形式。通过性能评估选出保证变形能力最好的方程。在此方程的基础上通过考虑一些相关参数的影响对该方程进行改进, 从而得出具有保证变形能力的抗剪承载力计算式。

1 试验数据信息

文中搜集了相关的钢筋混凝土低矮剪力墙试验数据共计301个[16-47]。依下列原则进行筛选: (1)水平荷载施加于墙肢平面内; (2)剪力墙最终失效模式为剪切失效; (3)试件为对称配筋; (4)试件无交叉筋。最终从301个试件中筛选出285个满足上述要求的试件。

图1 展示了250个墙肢基本信息的频数分布。由图可知试件的剪跨比变化范围0.3 ～2.1,轴压比变化范围0 ～0.31, 混凝土强度分布在13.66MPa ～66.33MPa 之间, 此外墙肢腹板厚度为45mm 至200mm, 纵向及水平分布筋配筋率由0 到2.7%, 250个试件中有6个试件仅包括水平分布筋, 4个试件仅包括竖向分布筋。

2 低矮剪力墙抗剪承载力计算公式

2.1 公式由来

文中应用试验数据对五组抗剪承载力计算公式进行性能评估。这五组公式分别选自中国《混凝土结构设计规范》(GB 50010—2010), 美国ACI 318-14 规范中11、18章的抗剪承载力计算公式, 欧盟EC08 规范及加拿大CSA A23.3-04 规范。五组公式抗剪承载力的计算均由混凝土项及钢筋项共同组成。由于篇幅, 公式具体形式见相应规范。

第Ⅰ组公式(公式Ⅰ)选自我国《混凝土结构设计规范》(GB 50010—2010)[8], 式中混凝土对抗剪承载力的贡献考虑了剪跨比λ 及轴压力N的影响。美国ACI 318-14[6]提出了两组半经验公式用于计算钢筋混凝土低矮剪力墙的抗剪承载力,本文公式Ⅱ为该规范第11章用于普通剪力墙的设计, 公式Ⅲ为该规范第18章中低矮剪力墙应用于抗震设计的抗剪承载力计算公式。公式Ⅳ为欧盟EC08 规范中[7]钢筋混凝土低矮剪力墙抗剪承载力计算公式, 有别于美国及中国规范, 欧盟规范对抗剪承载力的计算同时考虑竖向分布筋及水平分布筋的影响。公式组Ⅴ为加拿大CSA A23抗剪承载力计算公式[9]。

2.2 公式简化

由于本文将依据试验结果对上述五组抗剪承载力计算公式从保证变形能力的角度进行性能评估, 因此首先需对各国混凝土7 轴心抗压强度表达进行统一(fc为立方体混凝土轴心抗压强度,f′c为圆柱体混凝土轴心抗压强度), 依据文献[48]的分析结果, 二者之间可通过式(1)进行近似转换:

此外, 为便于性能评估需对上述五组公式进行归一化处理: 1)将抗剪承载力(V) 通过方程变换由剪压比表示; 2)钢筋贡献项中水平分布筋配筋率由水平分布筋配筋特征值表示(ρhfy/fc)。归一化后, 剪压比及水平分布筋配筋特征值的变化范围均在0 ～1 之间。五组方程归一化结果如表1所示。

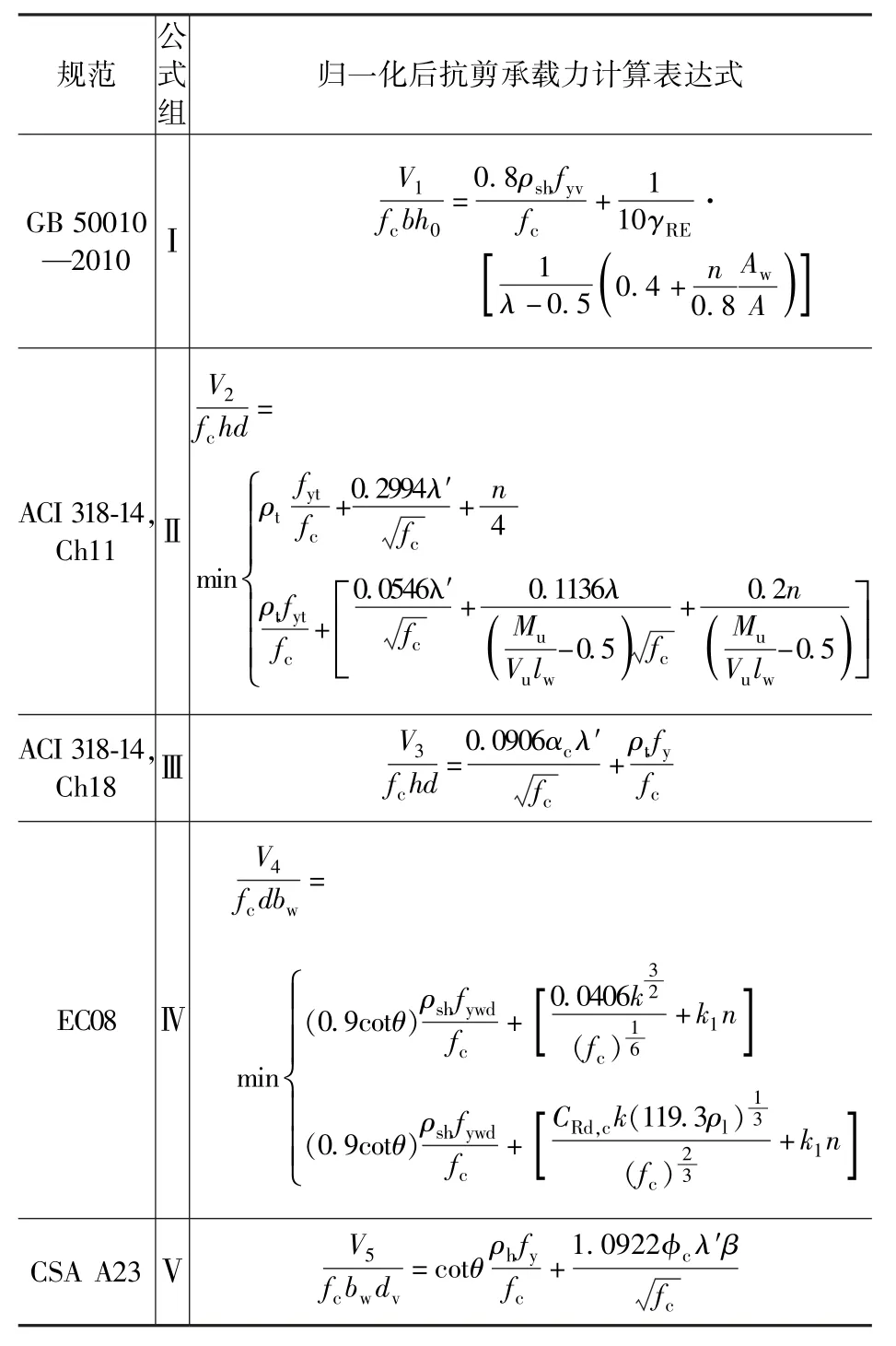
表1 剪力墙抗剪承载力归一化计算公式Tab.1 Normalized equation for calculating the shear strength of RC squat walls

3 抗剪承载力计算公式性能评估

从承载力计算误差及保证变形能力两方面对表1 公式进行性能评估。文中以考虑一定安全性的抗剪承载力计算误差作为承载力计算评估条件, 以试件的极限位移角是否达到1/120(基于GB50010—2010)作为变形能力控制条件。若极限位移角≥1/120, 则试件满足变形能力要求; 反之则不满足。为较准确地评估计算公式的性能, 将250个试件分别以轴压比及剪跨比为变量将试验数据分别分为3 组。以轴压比(n)为变量时,n= 0 时为第一组, 0＜n≤0.15 为第二组, 0.15 ＜n≤0.3 为第三组; 剪跨比(λ)为变量时, 0 ＜λ≤0.6 为一组, 0.6 ＜λ≤1为第二组, 1 ＜λ≤1.5 为第三组。由于当1.5 ＜λ时基本所有试验数据的极限位移角均大于1/120,为此将不在此范围内对抗剪承载力计算公式的性能进行讨论。

抗剪承载力应用“误差判别”计算式进行评估:

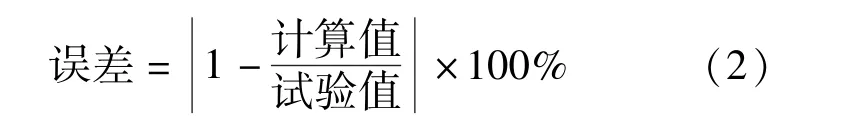
计算值与试验值之比以及承载力计算误差如表2 所示。由表中计算结果可知, 公式组Ⅰ及公式组Ⅴ所得计算结果与试验值的总体误差最小,且公式组Ⅰ及公式组Ⅴ的“计算值/试验值”总体小于其余计算式, 计算结果较为保守, 安全性较好, 对保证剪力墙在大震作用下的抗震性能较为有利。

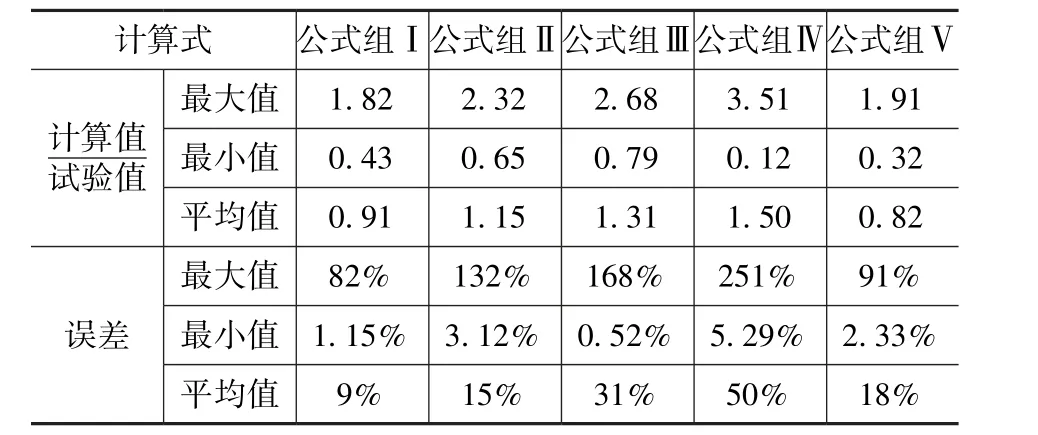
表2 承载力计算式与试验值对比Tab.2 Comparison of test results and prediction restults

此外, 应用“安全余度”的概念对计算式保证墙肢变形的能力进行评估:

“安全余度”即落在承载力计算公式上边界计算范围以上的实心点数与实心点总数的比值(见图2、图3), 比值越大保证墙肢变形能力越优。反之, 保证墙肢变形能力的性能越差。

图2、图3 中阴影部分上下边界由抗剪承载力计算公式所求上限值及下限值得出。

图3 试验与计算结果对比(剪跨比0 ～0.6)Fig.3 Comparison of measured results and five equation sets (aspect ratio=0 ～0.6)

依据公式(3)及图2、图3 试验数据情况,对公式组Ⅰ～Ⅴ的安全余度进行计算, 计算结果如表2 所示。由表可知公式组Ⅰ平均“安全余度”为84.11%, 相比其余公式“安全余度”较大, 保证墙肢变形能力较优。综合抗剪承载力计算及保证变形能力两方面, 公式组Ⅰ综合性能最优。然而所有公式“安全余度”均小于90%, 存在变形能力无法有效保证的潜在风险。为此有必要在公式组Ⅰ的基础上结合试验数据对其进行改进, 从而得到更能保证变形能力的抗剪承载力计算公式。

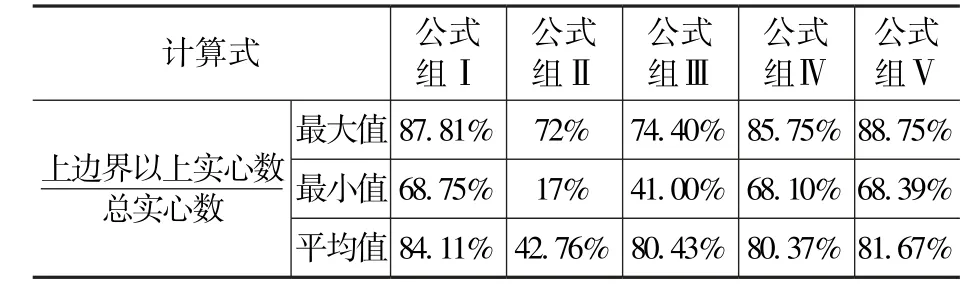
表3 “安全余度”评估结果Tab.3 Evaluation results of margin of safety

4 改进抗剪承载力计算公式

由第3 节分析得知公式组Ⅰ性能最优, 本节将对其进行改进以改善其保证变形的能力(即保证较少的实心点落入计算公式上边界以下的范围内)。

4.1 公式组Ⅰ的函数形式

由表1 归一化结果可知, 公式组Ⅰ实质是一个线性函数, 其简化表达式如式(4)所示:

式中:y为剪压比K为折减系数0.8;x为水平分布筋特征值ρshfyv/fc;B为与轴压比及剪跨比相关的抗剪承载力贡献项; 为安全考虑, 在此次研究中将Aw/A项的值取为1。

由公式(4)的函数形式可知, 为改进公式组Ⅰ的性能可选择两种方式: (1)调整折减系数K(即改变方程的斜率); (2)调整B对抗剪承载力的贡献(即上下平移线性方程)。然而通过对比得知公式组Ⅰ的斜率基本小于实心点的总体走势(蓝色线条)(以0 ＜λ≤0.6 为例, 见图4), 从性能评估的角度出发折减系数K取值相对偏于安全无需调整。为此选择平移线性方程对其进行改进。公式组Ⅰ中B的贡献与轴压比n及剪跨比λ有关, 因此可将B变化为B=BnBλ,Bn及Bλ分别为变量n和λ的函数且二者相互独立。下文将分别对函数Bn和Bλ进行改进。

4.2 函数Bn 的改进

由4.1 节可知, 改进Bn使计算公式组Ⅰ发生平移从而达到改进抗剪承载力计算公式性能的目的。以轴压比等于0 为例(图2a), 通过平移计算公式使实心点均高于计算公式的上边界。此时在不改变Bλ的情况下Bn取值0.033(图5)。利用相似方法分别得出轴压比为0.075、0.15、0.22 及0.3 时所对应的Bn改进值, 其计算结果如图6 中菱形标志所示。图中Bn随轴压比的变化近似为线性关系, 应用数理统计软件对其进行拟合得出Bn与轴压比之间的函数关系式:

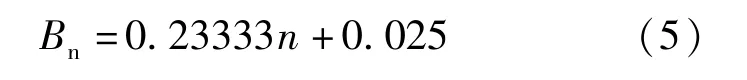
将式(5)带入式(4)可得:

图4 公式组Ⅰ与总体趋势对比结果(0 ＜λ≤0.6)Fig.4 Trends comparison of solid mark and equation setⅠ(0 ＜λ≤0.6)

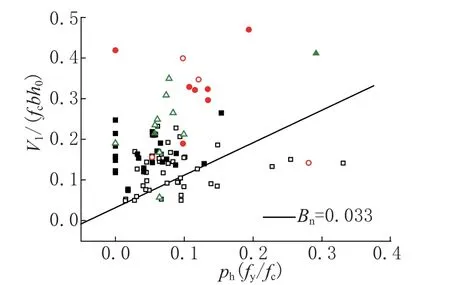
图5 Bn =0.033 的对比结果Fig.5 Comparison results ofBn =0.033

图6 Bn 拟合函数Fig.6 Fitting function ofBn

4.3 函数Bλ 的改进

图7 公式组Ⅰ不同剪跨比(λ)下的对比结果Fig.7 Comparison of equation setⅠand solid marks with different aspect ratio(λ)

当以剪跨比λ 为变量时,试验数据与公式组Ⅰ的计算结果如图7 所示。由图可知, 因其他区域实心标记均高于计算结果上边界, 只需对0.6 ＜λ≤1.0 及1.0 ＜λ≤1.5 两个区域进行Bλ的改进。其改进方法与Bn类似(将不同剪压比区域内计算公式上边界平移使实心标记高于此边界)。为得出图中Bλ与λ之间的函数关系式, 文中借鉴公式组Ⅰ中λ项的函数形式Bλ=a/λ+b进行拟合, 其拟合结果如式(7)及图8 所示:

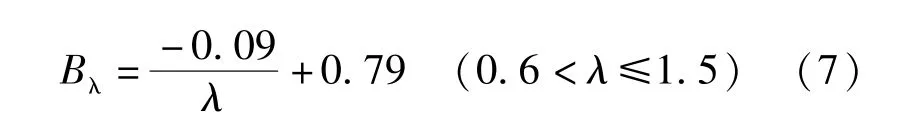
最终Bλ的表达式通过下列分段函数进行表示:

4.4 改进方程的性能评估

前文已在公式组Ⅰ的基础上对抗剪承载力计算公式进行改进, 其表达式如下:

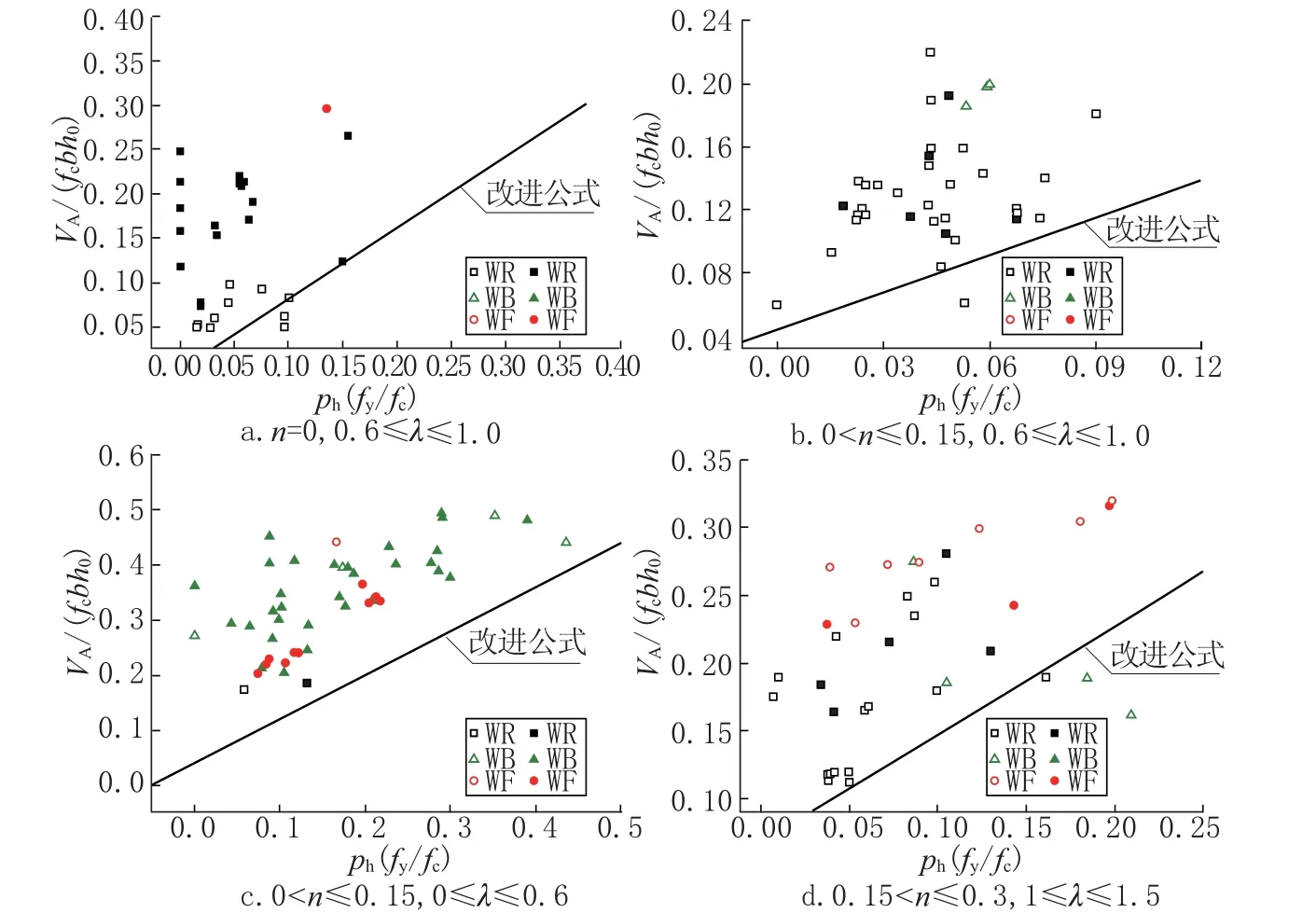
图9 改进公式的性能评估Fig.9 Performance evaluation of alternative expression

本文将对该公式从保证变形能力方面进行性能评估, 以验证其改进效果。图9 给出了几组典型的改进公式与试验结果对比。由图9 可知基本所有实心点均高于改进公式函数计算结果, 因此改进后的公式优于原公式组Ⅰ, 由此证明依据改进公式对钢筋混凝土低矮剪力墙进行抗剪承载力的设计能够更有利地保证剪力墙的变形能力。虽然此公式较优, 但其适用性仅局限于λ=0.3 ～2.1,n=0.03～0.3,fc=13.66MPa ～66.33MPa。此外该公式的抗剪承载力上限值及最低水平分布筋配筋率均依据GB50010—2010 确定。

5 结论

本文通过对当前应用较为广泛的抗剪承载力计算公式对比得知, 从保证构件变形能力的角度出发, 取自我国规范GB50010—2010 的公式组Ⅰ相比于其余四组公式更优。并在考虑轴压比及剪跨比两因素影响下, 对公式组Ⅰ进行了简单改进, 改进公式在保证变形能力方面得到了明显改善。