超声波作用下二维随机骨料混凝土模型损伤研究

陈启东 沈益晨 王力晓 刘鑫

(1.常熟理工学院机械工程学院 苏州215500; 2.苏州大学机电工程学院 215000)

引言

混凝土是目前城市道路与基础建设中应用最为广泛的工程材料[1], 其在年久失修与废弃的过程中给社会带来了大量的安全隐患和生态破坏。本文提出的超声波破碎混凝土技术, 具有适应性强、耗费低、能量大、方向性好等优势, 在废弃混凝土回收利用方面拥有较好前景。为了更好地分析混凝土在超声波作用下的损伤破坏机理, 有必要对其损伤力学性能做进一步研究[2]。

相关研究表明[3]超声波在固体中的形式传播一般是应力波, 并且在内部又会发生折射、衍射等现象。在近超声波加载端附近, 混凝土内部处于一种变形大、应变高的状态; 在远离加载端附近, 又处于复杂的应力环境。由此可见, 混凝土内部的瞬态行为极其复杂, 使得在超声波加载下其细观结构更易被破坏, 且很难被观测。Wittmann[4]最早将仿真模拟方法用于混凝土细观层次损伤分析中。随后, Bazant[5]等提出了随机粒子模型, 用于模拟固体颗粒材料的随机分布特性,并研究混凝土裂纹扩展过程。刘光廷、王宗敏等[6]借助蒙特卡罗方法生成随机骨料, 研究了混凝土试件单轴受拉条件下断裂过程。宋来忠等[7]基于骨料参数化理论, 运用级配理论分级投放骨料, 保证了骨料分布的合理性, 满足了高强度混凝土建模模拟的要求。Krajcinovic[8]将材料力学性能随机性的理论运用于混凝土损伤方面, 研究出连续损伤理论的统计特征。同济大学的李杰[9]在这个模型的基础上做出改进, 将单轴受力损伤模型和双标量弹塑性损伤模型结合应用, 并对混凝土非线性力学性能进行分析。目前针对超声波作用下混凝土损伤规律的的研究较少。

本文根据富勒级配曲线和瓦拉文平面转换公式, 运用ANSYS 经典界面中的程序语言编写了混凝土二维圆形随机骨料模型的程序, 并且将模型导入ABAQUS 有限元软件中。利用ABAQUS优良的非线性计算功能, 研究了混凝土在超声波作用下的破坏模式, 并对超声波幅值、加载区域大小、粗骨料粒径与体积分数对混凝土损伤力学性能的影响规律进行研究。

1 骨料随机生成与投放算法

目前最为理想的混凝土级配曲线是由Fuller等[10]提出的最大密实度级配曲线, 采用该密实度曲线能够使混凝土达到最优的密实度与强度。20 世纪初, Walraven[11]的研究工作将Fuller 提出的三维最大密实度级配曲线转换为二维骨料级配曲线, 并且计算得出试件截面内任意点具有骨料粒径D＜D0的概率为Pc(D＜D0)。

式中:D为骨料代表粒径;Dmax为骨料最大粒径;PK为占总骨料体积的百分比。

根据式(1), 在二维平面上, 能够计算出具有确定的骨料体积、不同筛孔直径D0下的混凝土具有粒径D＜D0的概率。

在确定骨料粒径分布概率之后, 还需要确定骨料二维随机生成与投放的参数: (1)根据骨料体积百分比PK、试件截面尺寸、骨料的粒径,计算所需骨料的数目; (2)确定每个骨料的圆心坐标xr=w·Rand(1)、yr=h·Rand(1),w、h为试件宽、高; (3)骨料相交判断[5,12]; (4)将上述坐标粒径存储于ANSYS 经典界面APDL 中, 并按照骨料相交判断原则, 在二维平面绘制骨料,并将模型在ANSYS 中生成的IGES 文件导入ABAQUS。

2 模型的建立

2.1 仿真模型

由于混凝土在超声波作用下的损伤分析, 是一个典型的非线性过程, 通常伴有明显的软化阶段, 常规的隐式分析方法解决此类复杂问题往往不够精确, 故采用显示动力学计算方法求解超声波作用下混凝土的损伤过程[2]。本文在Dynamic/Explicit 模块下模拟了二维圆形骨料随机分布的混凝土在超声波加载下的塑性损伤效应。采用三种不同截面尺寸, 分别为75mm ×75mm、100mm×100mm、150mm×150mm。图1 所示为截面尺寸100mm ×100mm 的仿真模型, 粗骨料体积分数占比为40%, 粒径为5mm ～10mm。网格划分尺寸为1mm, 划分方式为自由网格划分。

模型底部创建位移边界条件, 通过限制其在三个坐标方向上的位移与旋转达到固定底部的要求; 顶部加载应力载荷, 创建超声波频率的应力波以模拟超声波加载, 如图1 所示。为保证模型正常运算以及单元接触有效, 在模型接触模块中采用骨料与砂浆的绑定接触。

图1 仿真模型Fig.1 Simulation model

2.2 超声波载荷属性

混凝土模型顶部加载应力载荷, 同时创建超声波频率(＞20kHz)的应力波, 以模拟超声加载。在本文仿真过程中选择能量较集中的HANNING 窗调制的正弦信号且频率为20kHz,表达式为:式中: 时间t的单位是μs, 且为了不让信号发生重叠本文选取周期数n=5, 最终激励信号如图2所示。

图2 超声波激励信号Fig.2 Ultrasonic excitation signal

2.3 材料模型

1.混凝土塑性损伤本构模型

本文运用ABAQUS 的混凝土塑性损伤模型,该模型由Lubliner[13]提出, 这种塑性损伤模型在材料参数方面为混凝土结构的损伤研究提供了可靠的基础[14]。本文的仿真模拟参考刘海峰的模型参数与本构模型[2], 并把它转化运用于ABAQUS 材料属性中[15], 损伤时的有效应力为:

式中:d为损伤因子, 其值在0 到1 之间变化(无损到失效的变化)[15];σ- 为有效应力。

则单轴受力可表达为:

2.损伤因子的取值

当用ABAQUS 塑性损伤模型计算时, 用户需另外输入损伤因子—非弹性应变曲线参数。根据文献[16]中提供的混凝土应力应变曲线,综合能量等效原理可计算出损伤因子相关参数:

当x≤1 时:

3.本构模型参数选取及验证

参照文献[2]的数据, 水泥砂浆和粗骨料的模型基本参数见表1, 损伤因子及混凝土塑性损伤模型参数则由上述计算方法得出。由于骨料强度及断裂能相对较高, 采用线弹性模型来描述其应力应变关系; 而砂浆由于其易破坏的非线性特性, 使用混凝土塑性损伤模型来模拟[17]。

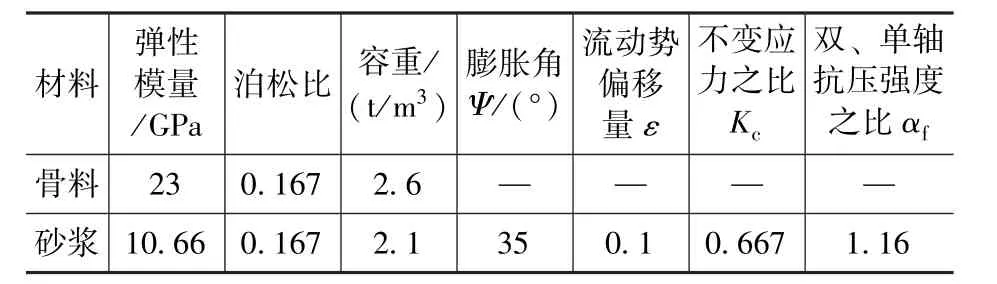
表1 模型参数Tab.1 Model parameters

图3 是以文献[18]的试验结果为参照与ABAQUS 仿真模型做对比。由图可知, 试验与仿真的应力-应变曲线在硬化阶段之前具有较高的吻合度。从软化阶段开始, 曲线开始分离, 这是由于仿真模拟采用侵蚀失效准则, 单元被删除后形成的空缺会一直存在[19], 所以抗压能力降低更快, 总体走势与试验相比较为契合。图4 为超声波加载条件下混凝土损伤破坏仿真与文献[18]试验的结果。超声波载荷加载于截面尺寸为100mm×100mm 的混凝土模型上, 在进行仿真模拟与试验时, 试件截面尺寸、粗骨料体积分数及粒径等参数保持一致。由结果可知, 试验的宏观破坏呈现顶部部分或完全破坏, 再由顶部向下延伸直至整体破坏, 该过程与本文所得仿真结果相符。经过与文献[18]试验的对比, 本研究所建立的仿真模型、设定的参数是可靠的, 可应用于超声波破碎混凝土激励研究。

图3 混凝土模型试验与仿真对比Fig.3 Concrete model experiment and simulation comparison

图4 混凝土破碎试验与仿真对比Fig.4 Concrete crushing experiment and simulation comparison

3 仿真模拟结果分析

3.1 混凝土的损伤破坏模式

进行了多组仿真对比, 发现混凝土的损伤破坏模式具有一定规律性, 以混凝土截面尺寸为100mm×100mm、粗骨料占比为40%、粗骨料粒径为5mm ～10mm、超声波幅值P为15MPa 为例。图5 显示出超声波频率为20kHz、加载时间为100μs 的损伤破坏云图。当t在20μs 至40μs时, 混凝土只在顶部产生轻微的损伤, 内部结构没有明显的变化, 并不会构成破坏。当t=60μs时, 混凝土内部结构开始受到影响, 骨料与砂浆交界处产生了明显的损伤, 损伤形状呈现细长条带状。当t=80μs 时, 损伤区域相互连接成片。此时, 超声波在到达底部之前虽然已经产生了能量, 但是这些损伤能量还不足以构成混凝土的破坏, 能量中的一部分经过反射回到试件顶部, 加强了顶部的应力应变场, 并促进新的损伤带产生、扩展。当t=100μs 时, 产生的能量已经大大提高, 足以破坏混凝土, 而且损伤形式已经从细长条带状变成大片的整体区块状, 损伤从超声波叠加的载入区开始, 并且向下蔓延。

图5 混凝土的损伤破坏过程Fig.5 Damage and destruction process of concrete

3.2 超声波幅值的影响

以三种不同截面尺寸混凝土仿真模型, 研究模拟超声波幅值对混凝土损伤力学性能的影响。超声波加载区域为30mm, 骨料占比为40%, 骨料粒径为5mm ～10mm。结果如图6 所示, 表明混凝土峰值应力与超声波幅值呈正相关, 混凝土峰值应力随着超声波幅值的增加呈现出逐渐增加的趋势。超声波幅值低时, 超声波产生的能量小,混凝土损伤较少, 超声波没有得到充分扩展, 扩展范围小, 因此, 混凝土模型的应力水平较低,峰值应力也较小。超声波幅值高时, 产生的能量较大, 瞬间产生损伤, 同时应力向四处扩展。所以, 混凝土表现出应力较大, 峰值应力相对较大。

图6 混凝土峰值应力与超声波幅值的关系Fig.6 The relationship between concrete amplitude stress and ultrasonic amplitude

3.3 超声波加载区域大小的影响

取混凝土模型骨料占比为40%, 骨料粒径为5mm ～10mm。对三种截面尺寸的混凝土模型在超声波幅值5MPa 下的损伤破坏进行模拟, 加载区域大小分别选取30mm、45mm、60mm。图7显示加载时间为100μs 时, 超声波加载区域大小对损伤破坏效果的影响。损伤其中表示单元初始损伤时的位移;表示完全失效时的位移;表示加载过程中最大的位移。

图7 表明, 同一时刻, 超声波加载区域越大, 混凝土损伤值越大。同时, 损伤程度随混凝土模型尺寸的减小而增大, 试件越小, 越容易受到损伤。这种现象的原因是: 当超声波加载在较大的区域中时, 超声波输入能量大, 且能量增长迅速, 产生过度的应力集中, 导致损伤值增加。反之, 在较小的加载区域中, 超声波能量扩展有限, 应力集中只存在于部分区域。再者, 混凝土强度随着模型尺寸的减小而降低, 而超声波在模型中传播的路径则越短, 也越容易造成损伤破坏。

图7 超声波加载区域对损伤影响的时间历程Fig.7 Time history of the impact of ultrasonic loading area on damage

3.4 体积分数的影响

取骨料粒径为5mm ～10mm, 加载区域为45mm, 以三种截面尺寸的混凝土模型为研究对象, 研究超声波幅值为10MPa 时, 混凝土粗骨料的体积分数对混凝土损伤的影响, 如图8 所示。从图中可以看出, 混凝土损伤随着时间的推移累积叠加, 呈现出先快速增长后缓慢累积的趋势。其中, 粗骨料体积分数为40%时混凝土的抗损伤能力最强, 损伤保持稳定增长。因为在该体积分数下混凝土配比最为合理, 且强度与内部应力最为稳定。而粗骨料体积分数为20%、30%时, 混凝土配比相对稀薄, 超声波在混凝土中的传播得到有效充分的扩散, 使其快速发生损伤和破坏。

3.5 粗骨料粒径的影响

以三种截面尺寸的混凝土模型为研究对象,超声波加载区域为30mm, 骨料占比为40%, 研究在超声波幅值为10MPa 时, 混凝土粗骨料粒径对混凝土损伤破坏的影响。

对骨料粒径做分段研究, 最小粒径保持不变, 最大粒径从10mm 至35mm 变化, 分析超声波加载下粗骨料粒径对混凝土损伤的影响, 如图9 所示。从图中可知, 随着时间的增加混凝土损伤先经历迅速变大的过程, 之后到达一定稳定值, 损伤趋于稳定。不同骨料粒径模型到达最大损伤所需要的时间各不相同。混凝土强度随着尺寸减小而越低, 对应的最大损伤值时间越短。因为在超声波能量较大的前提下, 混凝土模型尺寸越小, 超声波在其中快速损失破坏所需的时间越短。在所有混凝土尺寸模型中, 骨料粒径为5mm～10mm 时, 混凝土抗损伤能力最强, 达到最大损伤值时间最长。

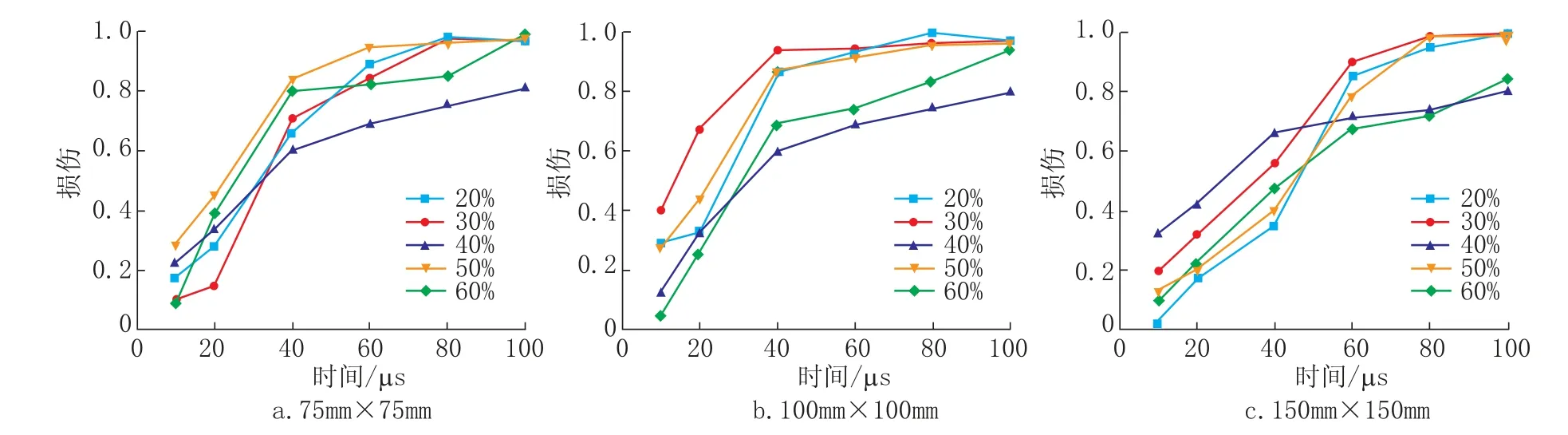
图8 混凝土粗骨料体积分数对损伤破坏的影响Fig.8 Influence of concrete coarse aggregate volume fraction on damage

图9 混凝土粗骨料粒径对损伤破坏的影响Fig.9 Influence of concrete coarse aggregate particle size on damage

4 结论

本文基于混凝土塑性损伤理论, 对超声波加载下混凝土内部的材料特性及损伤破坏的演化发展进行深入研究。运用APDL 语言编程, 建立混凝土骨料模型, 在模型上加载应力波形式的超声波, 分析混凝土的损伤破坏模式。本文研究了超声波幅值大小、加载区域、粗骨料体积分数与粒径对混凝土损伤破坏力学性能的影响, 得到如下结论:

1.超声波幅值增大, 混凝土内部应力也随之变大, 损伤逐渐增加, 形状由带状变为区块状,最终造成损伤破坏;

2.超声波加载区域增大, 混凝土试块随着输入混凝土内部的超声波能量的增加, 累积损伤更快, 损伤更容易形成;

3.混凝土粗骨料体积分数和粒径分别为40%和5mm ～10mm 是一个比较合理的数值。此时, 混凝土内部结构更趋于稳定, 抗损伤能力较强, 同等条件下, 超声波产生的破坏最低。