数据挖掘算法在河口羽状流数据分析中的应用*

李昭颖， 王厚杰

(中国海洋大学海洋地球科学学院，山东 青岛 266100)

作为河流携带的陆源物质向海洋输送的关键通道，河口羽状流(Plume)由自河口入海并浮于盐水上的低密度淡水形成，其在近场(Near-field)内的扩散状态作为河流动力学中的关键参数，决定着淡水、陆源沉积物、营养盐等在河口附近的分布状况和输运范围，对河口和近海物质输运与环境有重要影响[1-2]。特别是羽状流扩散角(Plume spreading angle)作为近场羽状流的关键特征将直接影响河流的回水过程，并决定了河口附近沉积物的堆积状态[3-4]。然而，囿于数据限制和技术手段，目前的研究多集中于理想条件下的定性分析[2]，数据来源以实验室数据和现场调查为主[1,5]，数据获取成本高、数量少，难以获得长期连续实际河口处羽状流扩散角的变化趋势，也无法就羽状流的动力因素进行显著性分析。鉴于此，卫星遥感数据以其大批量数据及长时间尺度的特征，为解译河口羽状流扩散趋势提供了新的方法。然而，针对遥感数据开展的传统人工处理方法存在效率低、误差大的缺陷，难以对海量数据开展批处理，亦无法提取数据背后隐含的规律性信息。因此，作为能够自动从数据中提取信息的方法，数据挖掘技术(Data mining)为解决这类传统难题提供了新思路，并已经在地球科学，特别是沉积学中获得了广泛的利用。以线性回归法为代表的数学算法在针对湖泊沉积物内有机碳的矿化程度以及周边环境因素的相关性开展分析[6]，针对沉积物的粒度、地球化学组分和物源分析中均取得了不错的效果[7-9]。概率算法主要包括最近兴起的机器学习技术，其中代表性的回归算法为随机森林(Random forest，RF)法[10]。作为统计学中新兴的、高度灵活的机器学习算法，随机森林在地球科学中的应用验证了其高效的分析能力，近年来在建立沉积物分布模型、推测河流流量等河口沉积动力学问题上初步展现了其强大的分析作用[11-14]。

然而，数据挖掘算法的加入在解决的问题同时也产生了新的问题。由于数据量和数据精度的约束，数据挖掘算法在解决地学问题时的表现效果尚待评估。同时，经典的数学算法和新兴的概率算法在不同数据集上的表现存在不一致性，我们需要根据数据集特点对数据挖掘算法的适用范围进行深入讨论。因此，在利用数据分析方法的基础上对其特点进行评估，对基于地学数据的数据挖掘算法的推广应用具有重要的意义。

本文以马格达莱纳河河口羽状流近场数据和周围环境因素为例，使用分属数学算法和概率算法的三种不同的数据挖掘方法，讨论方法结果之间的差异和产生原因并总结了其方法特征及应用范围，从而能够评估方法的表现效果、对模型输出结果作合理取舍。同时，基于对算法拟合效果及分析结果的探究，建立近场羽状流扩散角模型，探讨其长期变化趋势，分析扩散角的环境影响因素，从而进一步探讨现实河口下可能存在的沉积物分布与堆积趋势。

1 研究方法

针对河口羽状流主控因素这一回归问题，本文主要使用基于最小二乘法(Ordinary Least Squares，OLS)的多元线性回归(Multiple Linear Regression)，套索回归(Lasso Regression)以及基于决策树CART算法(Classification and Regression Trees，又称分类回归树)开展的随机森林算法对问题进行研究，前两种属数学模型，后一种为概率模型。

多元线性回归(简称MLR法)指对于因变量的预测中，具有两个以上的自变量对其存在影响。针对可以表示为式(1)的多元线性回归问题：

Y=BX+ε。

(1)

Lasso是一种采用了L1正则化(L1-regularization)的线性回归方法[15]，即满足最小二乘法的同时，通过L1范数t使得回归系数总体偏小，从而保证参数前的回归系数为较小值，而相关性较低因素的回归系数趋于甚至等于零。该方法能够有效的减小模型拟合结果的波动性，防止模型过拟合，并有效的对低相关性参数进行筛选。

基于CART算法的随机森林(简称RF算法)[10]是一种决策树的集成方法。令决策树为二叉树，依照决策节点划分为有限部分后在每部分上确定终端节点的概率分布，并采用系数[16]作为最优特征选择法。在决策树的基础上，RF算法使用Bagging算法(Bootstrap aggregating，引导聚集算法)进行重采样，并建立若干互相独立的分类器，最终以分类器的投票结果返回预测值，从而有效的改进了决策树所具有的问题。图1是RF算法的工作流程示意图。从数据集中有放回的随机抽取n个样本训练形成分类器，并利用其余数据对此时形成的树进行泛化性能测试。基于此，随机森林算法将反复执行此过程获取m个互相独立的分类器。针对第i个样本，分类器将分别从n类分类中给出预测结果。针对回归问题，该n个预测结果的平均值为最终预测结果。

图1 随机森林算法的主要结构示意图[10]Fig.1 The main structure of random forest algorithm

2 数据来源及预处理

针对河口羽状流近场扩散角的动力影响因素问题，本文将基于Landsat卫星图片数据和海洋模型数据，就马格达莱纳河及其河口周边的环境条件开展分析。

马格达莱纳河是哥伦比亚最大的河流系统，年际输沙量位于全球前十[17]。图2是马格达莱纳河附近的环境因素方向示意图。本文选择马格达莱纳河作为范例河流，主要是出于以下几点考虑。首先，马格达莱纳河位于南美洲北部，属于高含沙量河流，具有清晰的高含沙量羽状流，羽状流颜色与周边海域有明显区别，便于开展识别和探索；其次，该河流处云层遮盖较少，大部分Landsat卫星图像能观测到较为完整的河口羽状流形状，能够提供大量的连续的长期观测资料；最后，该河流为单一河道河流，河道经由人工介入后能够长期保持稳定，在研究时间内无出汊、改道现象，河道向海伸出，河口附近开阔，周围无岬湾遮挡，羽状流形状及扩散几乎不受周围地形影响。

(河道向外突出，为河流唯一的出海口，周围的海岸地形对羽状流无影响。图片来自于Landsat卫星2015年4月1日图像。 The channel protrudes outwards and is the only outlet of the river. The surrounding coastal geomorphology has no effect on plume. Image is from Landsat 8 satellite in April 1st, 2015.)

本文研究中，羽状流近场数据来自于1984—2018年间的Landsat卫星数据，主要针对羽状流在河口附近的扩散角进行提取。基于前人研究[18]，考虑到河口的实际情况，环境因素主要使用河流流量(Discharge)，风(Wind)，海流(Current)，波浪(主要指波高，Wave height)和潮汐(主要指潮高，Tide height)作为基本的边界条件进行分析，数据来源见表1附注。边界条件的时间跨度从1982—2018年，均基于马格达莱纳河所处位置进行提取，并对数据进行了日平均处理。为建立羽状流扩散角与环境因素的关系，选取可以使用数据挖掘方法进行分析的动力参数，图3是环境因素与羽状流扩散角之间的对比示意图。

在开展数据分析之前，为了满足回归模型的要求，需要对数据进行预处理。回归模型中，自变量数据要求与因变量之前存在弱相关以上的关系，且不具有多重共线性，无异常值。皮尔森相关系数(Pearson correlation coefficient, 简称PCC)是统计学中常用的参数，可以用于计算两个变量之间的线性相关性。羽状流与相关环境变量的具体信息见表1。由于多因素混杂的原因，相关性普遍处于较弱到中等相关的程度，但是这些环境因素与羽状流仍具有可见的相关性，可以用于下一步分析。值得指出的是，在两两比较的过程中，发现风速与波高之间的PCC达到了0.89，属于强相关，违反了不具多重共线性的原则。考虑到河口附近以风浪为主，风与浪一般属于共同作用，在下文的分析中，本文只选取风作为代表因素进行分析。除了风与浪之外的其他变量对之间相关性很弱，这表明他们对于羽流的控制和影响是相互独立的。为去除数据中的异常值，本文对所有的数据取Z-score值，并将Z-score大于3.5的值认为是异常值，并从数据集中删去[19]。同时，对数据取Z-score的做法，能够完成对数据的中心化和归一化，取消由于量纲不同、自身变异或者数值相差较大所引起的误差，并得到均值为0，标准差为1的服从标准正态分布的数据。

(从上至下分别为海流流速、波高、潮高、风速和河流流量。 From top to bottom are the current speed, wave height, tide height, wind speed and river discharge.)

同时，需要说明的是，在人工河道的限制和干预下[20]，除去河道口的东侧出现了沙坝堆积体，使得河口处逐渐发生转向之外，马格达莱纳河的河道在近40年内没有出现出汊、偏转的情况，始终指向北偏西的方向。考虑到该地形变化难以提取，且沙坝的堆积具有随时间不断增长的趋势，在进行数据分析的时候，酌情引入“年”(Year)作为参数之一。该参数与其他变量进行对比后发现，PCC最高的为河流流量，为，仍处于中等相关，不构成强相关关系，可以引入作为变量。同样的，在进行季节分析的时候，各因素的季节性变化并不一致。为了对羽状流进行季节性变化的控制作用，“月”(month)作为参数将被引入到下一步的分析之中。与其他参数对比之后发现，PCC最高的为风速，为，也处于处于中等相关，可以引入作为变量。

表1 羽状流及相关环境变量参数Table 1 The parameters of plumes and related environmental variables

最终，具有所有边界条件、能够参与下一步分析的数据组共计128组，且都进行了中心化，以确保参与模型训练时得到的参数结果能够代表该因素的贡献值。据被随机分为两个子集，分别是训练集(75%，包括 96 组数据)和测试集(25%，包括 32 组数据)，两个子集具有相似的自变量和因变量分布。

3 数据分析结果及适用性讨论

将进行预处理之后的训练组适用MLR线性回归法进行分析，针对羽状流扩散角得到了下述的方程(2)：

θ=-0.169 0×Uc-0.067 0×Q-0.227 6×Uw-
0.216 3×Ht+0.082 4×Month-0.405 0×Year。

(2)

之后，将训练组投入Lasso线性回归法进行分析。本文Lasso回归模型中参数t的取值为0.01，针对羽状流扩散角度得到了下述方程(3)：

θ=-0.138 3×Uc-0.060 6×Q-0.229 8×Uw-
0.182 5×Ht+0.056 3×Month-0.363 5×Year。

(3)

最后，将训练集用于RF概率回归法进行进一步分析。在本文的训练中，决策树数量为300。作为黑箱算法，RF只能根据算法内的决策树给出最终的拟合结果，而无法像线性模型一样得到具体的参数表达式。考虑到很多情况下仍然需要衡量各自变量与因变量之间的控制作用，Breiman于2001年提出了一种方法[7]，可以对进行过中心化和归一化之后的变量重要性进行排名，一般来说，在该分数中具有较大值的要素被认为对因变量具有更重要的控制因素。针对羽状流扩散角度的分数结果如下方程(4)所示：

RFmodel-θ:Year>Wind>Discharge≈
Current>Tide≈Month。

(4)

其中，重要性占比分别为，Year=0.25,Wind=0.23,Discharge=0.15,Current=0.15,Tide=0.09,Month=0.09。

根据以上三种模型，图4是三种方法所获的预测结果与测试集相比对得到的结果。可见，三种方法获得的结果类似，线性法与概率法的拟合结果虽然存在一定区别，但均能相对完整的拟合出测试集的变化趋势。然而，三种方法对于羽状流扩散角的分析结果及对动力因素的权重却存在很大区别，主要在于河流流量和潮汐的作用，即RF法结果中认为河流流量是紧随风速的第三重要的变量组成，而潮汐的重要性小于海流流速，与季节影响程度相当。考虑到评价效果的前提是结合问题背景，而近场环境的具体定义是河流初始动量大于外界动力影响的区域，因此在该区域内继承了河流动力学特征的羽状流会展现出明显的河流效应[18]。相比较而言，随机森林回归法认为无论是羽状流扩散角还是羽状流方向中流量都是排名第三的重要控制组分，其结果更具有说服力。同时，这也指示着流量对扩散角、方向的影响可能不是一元线性的，而是以多元线性或非线性关系相关。

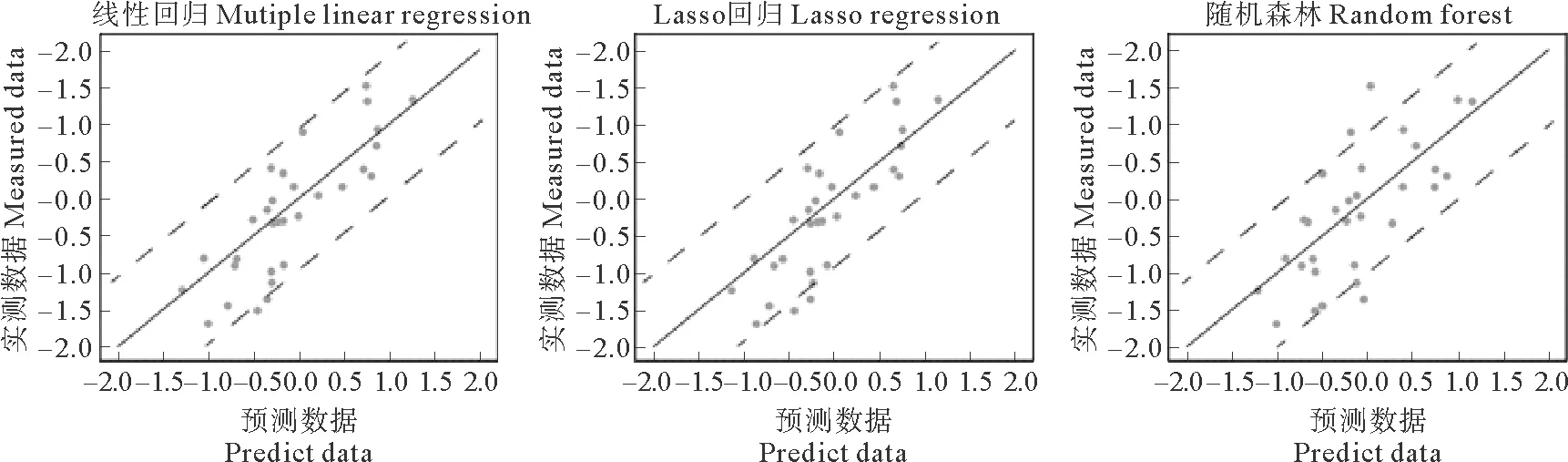
图4 利用MLR，Lasso和RF回归模型对羽状流扩散角进行拟合后与测试集的对比结果Fig.4 Comparison of fitting the plume spreading angle test set with MLR, Lasso and RF regression models results

出现上述情况的主要原因是线性法与概率法回归思路的区别。线性回归中，预测结果的主要思路是利用已有数据计算均方误差，并将均方误差最小值时的估计值作为结果，并给出此时各变量的回归系数。以随机森林为代表的概率法，则是针对各变量影响下的节点概率值作分析，最终得到的并非各变量的回归系数，而是其在森林中每棵树内的重要性。换言之，线性回归强调的是自变量和因变量之间的线性关系，最终能得到完整的数学结果，而随机森林侧重的是自变量对因变量的影响程度，单纯的只从形成结果概率上进行推算结果。

然而，仅从拟合结果上出发时，三种方法与测试集的拟合结果均具有可信性，甚至随机森林的结果略弱于线性回归：这体现了随机森林等新发展的机器学习技术的局限性，即数据量要求高。一般的线性模型仅需要十倍于变量的样本，而随机森林等新兴方法的数据集可能需要百倍于变量的数据集进行训练。本文的数据挖掘模型应用中，模型测试集的数量大概在100～115个左右，变量数目则在5～6个左右，这种较小的数据集对于线性模型而言更容易取得好的拟合结果，而随机森林方法虽然得到的结果更贴近前人已有研究，得到的模型拟合结果却弱于两个线性模型的拟合结果。

本文讨论的羽状流问题中，河口附近环境因素复杂，易受突发性因素影响产生变化。特别是针对某一时刻羽状流扩散情况的卫星数据，与囿于数据精度而多为日平均的环境因素相比，其控制作用受外界影响较大、精度较低。这也凸显了地学数据的特征：数据量小，数据精度低，噪音多。此时，基于概率的方法由于能够挖掘数据之间的控制趋势而效果更好，因此导致了随机森林算法具有拟合精度略低但拟合结果更符合实际的特点。从另一方面，同样作为机器学习方法，两种模型的适用条件存在区别。线性回归法更适合针对噪点少的小数据集开展应用，如实验室环境下产生的数据集，或者针对获取数据较不方便的环境下产生的少量数据，以分析自变量与因变量之间的数值关系，为进一步提取数值模拟模型作准备。而以随机森林为代表的概率算法系列，由于不需要考虑变量之间的线性关系，更适合针对较大量数据下的复杂环境开展分析，以获取自变量对因变量的总影响趋势，衡量变量的重要性。因此，当针对回归问题选择处理方法时，需要综合考虑数据质量和数据数量两方面的影响。对于以本文问题为代表的大部分地学数据而言，以随机森林为代表的概率法可能是更好的选择。同时，需要说明的是，无论哪种数据挖掘方法都无法避免由于数据精度和分辨率等问题带来的噪点，因此在进行讨论时必须注意到数据本身可能造成的误差。

综上所述，在近场地区羽状流扩散角的环境因素中，年际变化、风速、河流流量可能是最为主要的控制因素，随机森林模型的结果更适用于对以本问题为代表的地学数据进行讨论。

5 羽状流扩散角因素分析

基于上文得到的结果和方法对比情况，可以对羽状流扩散角的影响因素进行分析，并开展进一步模拟。对于马格达莱纳河羽状流的近场扩散角而言，年际变化、风速、河流流量为最主要控制因素，文中得到的结论与前人的研究结果能够互相对应。

羽状流扩散角主要指羽状流在河口附近向两侧扩散的范围，该扩散过程通常不改变羽状流底部的湍流混合过程，但会在表面显著增加羽状流与下层水体的混合面积，降低羽状流的平均密度，增加河水的净稀释度，从而加强近场内的混合过程[5]。需要说明的是，此处的年际变化，主要指马格达莱纳河口处逐渐出现的沙坝沉积，迫使河流的入射流量方向逐渐由北向西北偏移。河流流量及河流指向方向对羽状流的扩散角所具的负相关影响与文献[1]和[21]的研究结果类似，河流流量及其入射角会对羽状流扩散速率产生明显影响。如图5所示，在河流流量较低或者河口堆积体较少的情况下，羽状流具有更大的扩散角，此时河流的河道和近海羽流区域均趋向沉积；而在河流流量增大或河口堆积体增多的情况下，羽状流扩散角小，河道发生冲刷，在近海的羽流区域出现自通道化，并趋于形成堤岸。相比之下，以风速和海流为代表的海洋动力所产生的外应力在近场内对羽状流同样具有重要控制作用。Xia等[22]的研究中指出，在强烈的风应力下，河口流出的淡水进入沿岸流的量显著增加，而Kakoulaki等[23]认为风应力在近场内是排名第二的重要因素。同时，必须要注意到的是，马格达莱纳河处平均风速高达6 m/s，属于绝对的高风速地区。Xia等[22]的研究表明，在风速大于5 m/s时，随风力增加，羽状流的扩散面积必定减小，这也会造成羽状流扩散角的进一步降低。图5显示，在强烈的侧向应力作用下，羽状流更倾向于沿风速方向输运，大部分淡水会进入沿岸流，造成其东侧出现明显的空白，在马格达莱纳河口的环境下即为羽状流逐渐向左偏转从而造成其扩散角变小。本质上，河口羽状流的扩散状态是初始动量与外界环境因素竞争的结果，因此河流流量较大时，羽状流的初始动量高，在离开河口时具有更强的径向速度，因此倾向于维持本身的状态；而在河流转向后，其入射角方向会与风速、海流等趋同，反向增加了外力的作用。

(从上到下分别是河流流量/海流、风速、年份变化时对应的扩散角示意图以及相对应的羽状流卫星图片。 From up to down are discharge/current, wind, year and satellite images.)

根据计算发现，羽状流在近场扩散中，羽状流宽度与距离河口的径向距离成比例[24]。换言之，我们可以以等腰三角形作为羽状流的模拟，以高度抽象的方式展示羽状流扩散角的变化趋势，并讨论羽状流对于河口-海岸带的影响。图5同时展示了马格达莱纳河羽状流在21年内的羽状流扩散角变化所作的示意图，为保证稳定条件，环境因素取平均值，季节统一为春季。图中的模型结果显示，羽状流的扩散角随年份变化不断减小，这一趋势与卫星图片所展示的河口卫星图像是一致的，这也会影响河流的回水面积，从而影响河口的沉积过程。在羽状流扩散角不断减小的过程中，如果不存在人工疏浚等外界影响，马格达莱纳河河口将由大范围的水下三角洲沉积逐渐转变为河道沉积体，进一步形成向外延伸的鸟嘴状河道，渠道化更加明显。同时，河口西侧的羽状流扩散面积，即淡水和沉积物的主要影响范围，在研究时间内处于不断下降的趋势，但下降幅度不高；相比之下，河口东侧的羽状流扩散范围随时间变化产生了显著的降低。卫星图片显示，产生这一变化的主要原因在于，随时间变化河口右侧逐渐出现明显的沙坝堆积。考虑到马格达莱纳河附近的海洋动力，包括风、海流等均呈现自东-东北向西-西南方向的趋势，当高含沙量的淡水水体自河口排出后，会在河口右侧迅速混合、减速，并产生沉积，这可能是沙坝产生的原因之一。随着羽状流扩散角度的不断减小，河口右侧逐渐脱离羽状流的影响区域，沙坝的沉积速率可能会显著降低。

根据模型结果可以对马格达莱纳河河口的未来变化趋势作一定推测。当河口进一步向左偏向，羽状流的扩散范围进一步降低时，河口东侧的沙坝可能会逐渐停止沉积，使得河流流量保持相同的方向而没有明显的变化。此时，羽状流的年际变化会收到明显的影响。同时，在Wright[2]的研究中，曾对羽状流的最小扩散角进行过计算，即河口羽状流的扩散角不会小于24.5°，因此范例河流处的羽状流扩散角度模型应以24.5°作为另一个限制条件。

需要说明的是，模型中所使用的“年”作为变量，主要代表河口的方向变化。但马格达莱纳河及其附近环境受厄尔尼诺-南方涛动现象(ENSO)影响显著，因此不排除年际变化中可能包含全球气候变化的可能性[20]。而模型中显示的季节差异除环境因素本身所具有的季节性变化效应外，可能与海洋中的温盐变化等因素相关。

根据马格达莱纳河的结果可知，羽状流在真实河口处的扩散角明显受环境因素影响。因此，在综合建立马格达莱纳河口及海岸附近的沉积物分布模式、讨论河流的具体变化趋势时，可以依照本文所得到的环境参数，针对不同环境因素赋予不同权重，从而实现该研究区域内更精确的推断和模拟。同时，在针对其他具有明显羽状流的大型河流开展研究时，可以有针对性的根据河口位置获取数据，依照上文中的分析过程和具体步骤进行环境因素权重分析，并探讨其随时间和季节变化呈现的羽状流特征。

6 结论

针对真实河口下近场羽状流扩散角的影响因素和变化趋势，本文利用马格达莱纳河羽状流及周边环境因素数据使用数据挖掘方法进行分析，并根据两种线性回归法和随机森林法的具体表现提出了根据数据来源、数据量和数据特征选择不同挖掘模型的思路，最终对马格达莱纳河羽状流扩散角的动力因素进行权重分析，并建立了羽状流扩散角时间序列模式。主要得到了以下结论：

(1)数据挖掘算法在河口环境下能够就复杂因素开展高效而准确的分析。在使用时，需要保证变量间不具有多重共线性，数据无异常值，并对数据进行中心化和归一化的预处理。最终得到的结果能够为进一步探究河口羽状流控制因素、建立羽状流扩散模型提供参考。

(2)作为数据挖掘技术的不同分支，线性回归法和随机森林法在数据分析上各具优势，需要根据数据集的特点进行选择。线性回归模型更适合针对噪点少的小数据集开展应用，而以随机森林为代表的概率回归模型更适合针对较大量数据下的复杂环境开展分析。针对类似问题选择方法时，需要综合考虑数据质量和数据数量两方面的影响。

(3)对马格达莱纳河的羽状流扩散角而言，最重要的影响因素为河流指向方向，其次为风速，再次为河流流量大小和海流流速，在进行针对该河流的沉积物分析时需要注意按不同权重增加环境因素的影响。同时，羽状流的变化趋势表明，随时间增长羽状流的扩散角度减小，河口物质的影响范围逐渐减弱，该河流在研究时间段内存在由大范围的水下三角洲沉积向渠道化的河道沉积变化的趋势。