基于格雷码光栅法的形貌扫描研究

陈益松， 夏 明， 沈 丽， 冯莲娣， 张龙女， 冯蕊琪

(东华大学 a.服装与艺术设计学院； b.现代服装设计与技术教育部重点实验室，上海 200051)

物体形貌扫描多使用结构光主动三维测量技术[1-2]，不同于相移、傅里叶等需要光栅相位调制与解算的间接三角法，基于编码图案结构光[3]的直接三角法由测量系统的几何关系并通过光面方程和共线方程来解算交线条纹的点坐标，重构物面轮廓[4-5]。

以格雷码编码的矩形光栅法属于使用面结构光的直接三角法，其黑白矩形光栅条纹边沿构成的光面与物体相交形成多条变形条纹。然而在实际解算过程中存在交线光纹识别并与光面方程匹配的问题，条纹密度越高，解析度也越高，因匹配不正确而出现解算错误的几率也越高。

已有许多文献使用3D Max、 Matlab等软件仿真测量和解算过程[6-7]，这虽简化了研究过程，但也存在模拟条件与实际情况不符，以及无法展现实际解算过程中可能出现问题的情况。

本文综合考虑投射和摄像装置的特点，以平行光轴系统结合移轴和局部偏置拍摄技术搭建了人台测量的试验装置，结合共线方程和光面方程，对矩形光栅条纹格雷码编码及运用原则、移轴投射、偏置摄像、镜头参数测量、交线条纹图像处理以及实际解算过程进行探索研究，并取得了预期的结果。

1 矩形光栅的格雷码编码

文献[8-9]最早提出使用格雷码(Gray code)对时域投射光栅进行编码，由于格雷码独特的性质，其编码光栅的边缘不重叠，因此没有条纹边沿间的相互干扰，从而减少了排序过程中可能的逻辑错误。文献[10]给出了格雷码与二进制码之间的转换关系。

运用格雷码编码的光栅需要由宽到窄依次投射，如图1所示。

以迭代算法为基础，可得到所投射光栅边沿序号的公式[11]，如式(1)所示。

k=2n-i(2j-1)

(1)

式中：k∈(1， 2n-1)为边沿排列序号；n为图像幅数；i∈(1，n)为图像序数；j∈(1， 2i-1)为每幅图像的条纹序号。

将式(1)进一步变换得：

k=2n-i+(j-1)2n-i+1

(2)

将(j-1)由十进制转变为计算机可识别的二进制，如式(3)所示，则得到文献[12]所介绍的光栅投射时序可执行编码中条纹边沿排列序号求取算法。

k=2n-i+((G0G1G2…Gi-1)2)10×2n-i+1

(3)

式中：Gi表示k条纹边沿所对应第i幅图像所在位置二值化后的灰度值(黑色为0，白色为1)，其中定义第0幅图像的灰度值为G0，G0的取值可以为0或1。但在计算过程中：若G0=0，则可直接按照式(3)进行计算；若G0=1，则在进行格雷码转换成十进制数字的过程中需要进行一步反射。括号外的下标2和10分别表示将该格雷码转换成二进制代码和再转换成十进制直观数字。例如，投射4幅光栅图像，计算第4幅图像中的第5个边缘：(j-1)十进制为4，转换成二进制码为0100，再转换为格雷码G0G1G2G3为0110，由式(2)和(3)计算得k=9。

2 测量系统设计

2.1 试验装置架构

本试验系统是由摄像机、LCD投影仪、人台及遮挡黑布等器材组成。

在一般交叉光轴系统中，虽然有效测量区域大，但存在光栅投射非线性分布问题。在相位法中，需要复杂的非线性校正[13]；在面结构光直接三角测量法中，也存在投射的光栅分布不均、光面方程难以构建的问题。本文采用平行光轴系统，结合投影仪的移轴投射及摄像机的区域偏置拍摄(相当于镜头移轴)，不仅可以使系统的校正得到简化，也可以扩大有效测量区域[14-15]。同时，由于摄像机和投影仪的镜头的景深区域均垂直于光轴，可以使两者的景深区域重合并有效地将人台纳入其中。

试验系统的测量坐标系如图2所示，选取物空间坐标系与投影仪坐标系重合。在实际系统校准中，以垂直墙面为参考面调整投影仪，使其投影图像的对角线完全相等，摄像机光轴与投影仪光轴平行，且投影仪镜头光心与摄像机光心在同一垂线上。

2.2 镜头参数解算与系统校准

实际操作过程中，投影镜头和摄影镜头并不是具有明确的光心位置的薄镜头，而是具有前主点cf、后主点cr及光心距d的厚镜头，镜头前边沿与前主点存在的距离为x，镜头的摄距为对焦平面P到镜头前沿的工作距离W与x之和，如图3所示。因此，确定x值是准确构建测量系统几何关系的必要条件。由于前主点可视作为薄透镜的光心，后续成像可按理想透镜处理(此时d=0，x可简称光心距)。

设投影镜头的焦距为fp，镜头在聚焦平面P1的投影高度为H1，P1与镜头前边沿的工作距离为W1，后主点至像面的像距为S1，将镜头聚焦点沿轴线移动一个距离至聚焦平面P2，则参数分别为H2、W2和S2。由于像面尺寸固定，则根据高斯方程和三角相似关系得：

(4)

(5)

(6)

(7)

由式(4)～(7)联解可以得到光心距xp的计算公式如式(8)所示。

(8)

虽然投影仪通常并不提供镜头焦距参数，但只要能查证到其使用LCD芯片的尺寸，亦可通过上述方程组解得：

(9)

同理，摄像镜头的光心距xc及焦距fc可以通过拍摄不同工作距离下对焦平面的固定尺寸的标板，由式(10)、(11)分别计算得到。

(10)

(11)

式中：I1为在工作距离W1所拍固定高度H标板的像高；I2为在工作距离W2所拍固定高度H标板的像高。

根据设备已知参数，经过测量与计算，可以得到完整的系统参数。设备与系统的参数如表1。

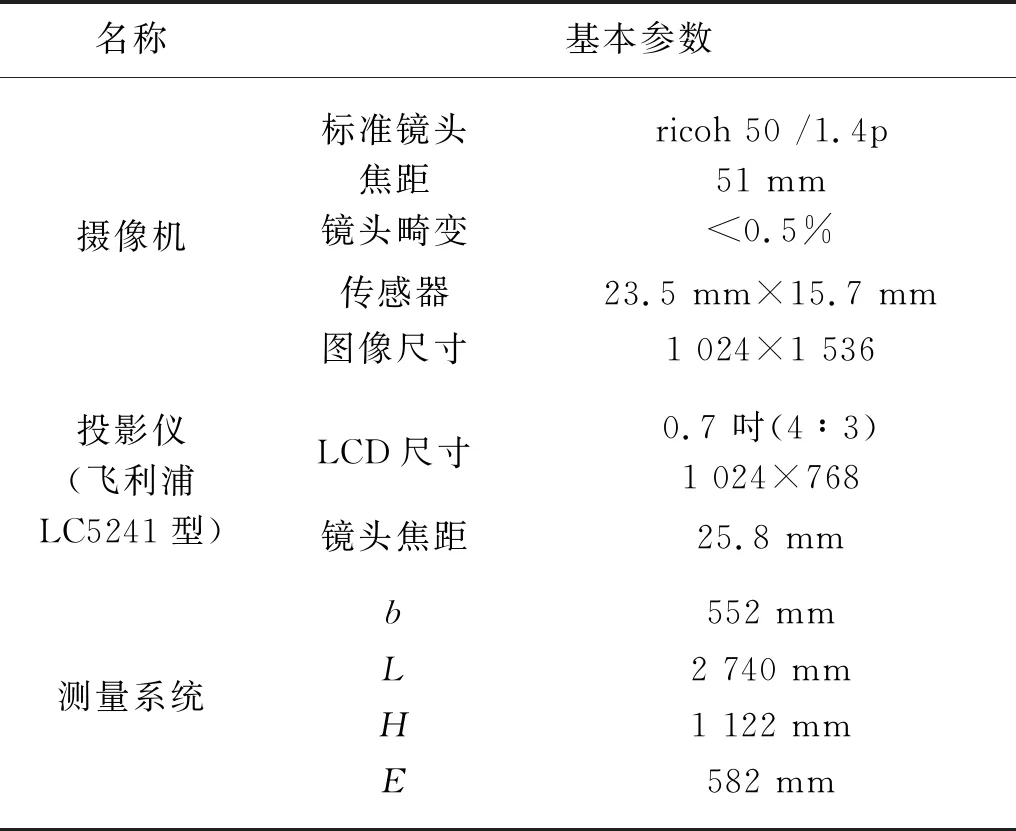
表1 设备及系统参数

2.3 共线方程

在摄影测量中，共线方程确立了摄像机图像坐标系和物空间坐标系的逻辑关系，如式(12)所示[16]。

(12)

式中：[xw，yw，zw]和[x0，y0，z0]分别为物点和摄像机光心在物空间坐标系中的坐标；[X，Y]为物点在图像坐标系中所对应的坐标；R-1为摄像机坐标系与物空间坐标系之间的旋转变换矩阵；zc为物点在摄像机坐标系z轴中的坐标；l为摄像机镜头像距。

根据图2的坐标系，摄像机坐标系和物空间坐标系x、y、z轴的方向完全一致，则旋转矩阵R-1为

(13)

摄像机光心[x0，y0，z0]在物空间坐标系的坐标为[0，b， 0 ]。

根据镜头成像的高斯公式得：

(14)

将式(13)和(14)代入式(12)并转换为代数形式，如式(15)和(16)所示。

Lfxw-(L-f)Xzw=0

(15)

Lf(yw+b)-(L-f)Yzw=0

(16)

由式(15)和(16)可知，一个摄像机所构成的两个代数方程(共线方程)无法解出物点的3个空间坐标值，但确认了物点、光心、像点共线。

2.4 光面方程

光面方程是投射的光栅黑白边沿构成的光面在物空间坐标系下的数学表示。

现有的许多模拟仿真研究都是选择中心投影的投影仪，然而在现实中基本采用固定移轴式投影仪，即投影镜头光轴(简称投射光轴)偏离图像中垂线一定距离。本试验采用常规的非对称式移轴式投影仪，并提出了非对称式投影中投射角的计算方法。

光栅移轴投射如图4所示。根据图4的几何关系，光栅某一条纹边沿的光面与水平面的的夹角α存在下面关系：

(17)

(18)

式中：α为第k条条纹边沿与投射光轴的夹角；β为投影仪的移轴偏置角，即图像中点和镜头光心连线与投射光轴(水平)的夹角；L为镜头对焦摄距；H为参考平面影像的高度；E为参考平面图像中心到投射光轴的距离。

投影仪坐标系与物空间坐标系重合，所投射的矩形光栅边沿光面方程，如式(19)所示。

yw=-zwtanα

(19)

将式(17)和(18)代入式(19)，可得到以条纹边沿序号k所表示的光面方程，如式(20)所示。

(20)

2.5 物体轮廓点坐标解

由共线方程式(15)、(16)和光面方程式(20)可知，在获得k光面与物体交线的像点坐标[X，Y]后，可通过上述方程的联解解算出所对应的物体表面的空间坐标[xw，yw，zw]。

3 图像处理与人台扫描点云

试验以黑布作为背景并在暗室进行，使人台仅接受结构光的照射。选择n=8， 即依次投射8幅图像，共计256条条纹。通过布尔运算得到各光面与物体相交的图像点所构成的变形条纹。

依据格雷码光栅依次投射的原理，可以得到第一条(k=2n-1)交线条纹的像素点，以此为基础分别向上和向下搜索第二幅图像2个k光面所生成的交线条纹的像素，然后再以已赋值条纹的区间为区域搜索下一幅光栅图所对应k光面的交线条纹的像素点，直到完成所有图像交线条纹的像素点搜索。由此解决像素点与对应的条纹边缘序号k值的匹配问题。

然而，由于阴影、暗点等因素，逻辑运算出的条纹通常存在多余点或缺失，即线条不是由连续单像素构成的理想条纹。当条纹密度较高时，还会出现匹配错误，因此要对条纹像素进行预处理[17-18]，必要时需要手工干预。最后运用Canny算法来提取条纹。

经过删除重复点和插补缺失点的修正后所提取的交线条纹如图5所示。由图5可知，如果从BC线条向下搜索，必然会在条纹EG中出现EF段的盲区，不能使被搜索的条纹完整再现。若条纹BC两端添加AB和CD两辅助线段，使搜索区域由BC段扩展到画幅两端，则可搜索整个画幅像素。因此，由第一条解算出的条纹开始添加辅助线段是后续条纹匹配解算的关键。

图6(a)是以黑背景全白光拍摄的图像(人台头上部较多的空白是区域偏置拍摄所致)；图6(b)是经过反二值化处理的图像；图6(c)为经过处理后得到有效解算区域(空白部分)，即后期图像条纹的处理和解算都限制在该区域。

图7(a)为投影的矩形光栅图像；图7(b)为通过布尔运算得到光面与人台的交线条纹，存在重复、断点等缺陷；图7(c)为经过处理后且添加了辅助线段的规整化条纹(参考图5)，该条纹上的图像坐标[X，Y]都是唯一确定的。

根据2.4节解算原理步骤，借助文献[19]给出的具体解算程序，即可解算出人台形貌的空间坐标点云数据，如图8所示。从不同的角度看，在人脸比较复杂的五官特征以及身体胸部肌肉形态上都有比较准确的形貌体现，证明本文的试验装置和解算方法是有效的。

4 结 语

本文针对格雷编码的矩形光栅的物形扫描方法做了进一步的理论分析，给出矩形光栅条纹边沿序号的一般表示法转化为时序可执行编码的推演过程。以平行光轴系统结合移轴和局部偏置拍摄技术构建了形貌扫描试验系统，提出了试验镜头参数的现场测量方法和基于移轴光栅投射的光面投影角的计算方法，使测量系统以及基于该系统的共线方程、光面方程可以在参数完全已知的条件下准确构建，减少测量误差。通过对交线条纹的提取、处理和识别，并利用共线方程与光面方程的联合解算，得到了试验人台三维数据点云，人台比较复杂的面部结构和躯体的肌肉形态均得到了较好的再现，证明了基本方法的可行性和系统的有效性。