低真空管道磁悬浮列车热效应仿真分析研究

张俊博，李红梅，王俊彪，宣言

（1.中国铁道科学研究院研究生部，北京100081；2.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心，北京100081）

0 引言

为主动顺应技术发展趋势，许多国家先后开展了磁悬浮列车的研发工作，并取得了一系列令全世界瞩目的成就［1-2］。然而，当列车处于开放空间大气环境下高速运行时，要面临与速度的平方成正比的空气阻力［3-4］和与速度六次方成正比的噪声［5］问题，当速度等级达到600 km/h以上时，在经济性和环保性上无法达到商业运营的需求。因此，构建低真空下的磁悬浮列车运行环境以减小阻力和噪声、获得更高的经济运行速度是实现更高速度轨道交通技术的重要发展方向。

在抽成低真空的管道中运行时，磁悬浮列车提速过程中面临的气动阻力及噪声问题将大大降低，然而车辆高速运行过程中的气动效应和车上发热设备产生的热量会积聚在密闭低气压管道内，无法自由扩散到大气中，温升过高会对磁悬浮列车的正常运行产生影响。因此，在对低真空管道磁悬浮列车的研究中必须考虑热效应影响，对热效应产生的危害进行及时预测与防护，以保证列车正常运行的安全性和可靠性。刘加利等［6］采用三维可压缩模型研究了真空管道高速列车气动热效应与列车速度、阻塞比和管道压力的关系。贾文广等［7］采用三维可压缩模型研究了真空管道高速列车气动热压耦合与列车速度、阻塞比和管道压力的关系。目前，还没有低真空管道磁悬浮列车综合热效应的三维数值模拟。采用三维可压缩模型对低真空管道磁悬浮列车的气动热效应及各种发热器件的热效应进行数值计算，主要研究列车运行速度、阻塞比和管道真空度对列车热效应的影响。

1 数值模型分析

1.1 基本假设

（1）进行仿真计算的磁悬浮列车速度区间为600～1 000 km/h，即管道内流体与列车的相对运动速度区间为600～1 000 km/h，经计算，流场雷诺数大于105，为湍流流动［8］，采用k-ε双方程湍流模型对流场进行模拟。

（2）管道内低压气体与列车的相对运动速度区间为600～1 000 km/h，流体流速大于0.3倍的马赫数，且流动状态比较复杂，其密度会发生明显变化，所以采用可压缩气体作为仿真介质。

（3）磁悬浮列车的外形对热效应计算结果的影响较小，忽略列车衔接处的缺陷及车上悬浮装置的模型细节，假设列车外表面为光滑平顺的几何型面。

（4）低真空环境初始温度300 K，管壁绝热，由于在常导制式下，地面直接给固定轨道供电，通过提高轨道上的供电电流频率提升列车速度，所以列车速度的提升导致轨道发热量增加，不考虑速度变化下的列车发热功率变化，车上悬浮导向电磁铁、夹层电器设备等发热设备的总热量约1 060 kW，并且热量充分扩散至管道内。

（5）由于网格数量较多，直接进行动网格计算的计算量较大，对计算机配置要求较高，为了降低计算量且不影响计算结果，假定列车不动，管道壁面与管内流体相对列车以列车运行速度运动的方式进行模拟。模拟了流体气动生热及流动换热的仿真条件，使其对热效应的仿真结果影响最小。

1.2 数值模型

采用适当简化的列车模型，头车-中间车-尾车3节编组形式，列车总长度为78.00 m，宽3.30 m，高3.50 m，横截面积11.55 m2，其中列车头部长27.00 m，头部流线型长度为15.00 m。整列车的列车表面均为光滑曲面，简化列车衔接及其他部位的几何缺陷，列车三维模型见图1。

图1 列车三维模型

考虑管道在低真空条件下的内部均匀受力问题，管道截面形状采用圆形，磁悬浮列车位于管道中心。为避免流体在管道中流动时入口区域（不稳定区域）的影响，车头距离管道入口222.00 m；考虑到流体流经列车后的稳定性问题对计算结果的影响，车尾距离管道出口900.00 m。管道全长为1 200.00 m，圆形管道横截面积随着阻塞比的变化而分别取不同数值。由于真空管道采用圆柱形管道，车体采用前后对称的流线型车体，因此网格划分采用结构化网格，管道与车体衔接处网格尺寸最小，管道区域采用层网格划分，这样的网格划分更加规则，生成网格质量较好，所有网格内部点都具有相同的毗邻单元，计算结果更容易收敛，适当减少网格数量对计算结果几乎不产生影响，大大降低了计算量，计算区域见图2。

图2 计算区域

1.3 数值计算设置

列车车体材料采用铝合金，根据假设管道壁面为绝热状态，管内气体采用理想气体，车上发热设备总热量为1 060 kW，管道入口和出口均设置为压力远场边界条件，速度大小为相应的列车运行速度，管道壁面设置为移动壁面，速度大小为列车运行速度，初始温度设置为300 K，列车表面设置为固定壁面。

列车表面散热可视为高速空气在管道内的强制对流换热，选用最普遍的关联式迪图斯-贝尔特（Dittus-Boelter）公式［8］:

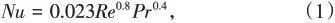
式中:Re为雷诺数；Pr为普朗特数。对流换热系数计算如下［8］:

式中:λ为导热系数，空气的物性参数；d为特征长度。

车体与管道整体截面形状为环形，采用当量直径作为特征长度，当量直径计算如下［8］:

式中:Ac为管道流动截面积，m2；P为湿润周长，即流体与管道壁及车体接触面的长度，m。

通过计算，得到不同工况下车体表面对流换热系数。阻塞比为0.2、运行速度为600 km/h、真空度为0.01atm的运行工况下，换热系数最小为4.11；阻塞比为0.4、运行速度为1 000 km/h、真空度为0.30atm的运行工况下，换热系数最大为109.68。模拟计算采用SIMPLE算法，迭代次数800，判断收敛的标准为能量方程，计算收敛时达到热平衡状态。

2 热效应数值计算及分析

2.1 计算工况

对同一磁悬浮列车模型在不同阻塞比（0.2～0.4）、真空度（0.01atm～0.30atm）下以不同速度（600～1 000 km/h）运行时进行数值计算，计算达到热平衡时列车表面最高温度及管道内部的温升情况。仿真工况条件见表1，共计算了33个工况。

2.2 数值计算结果

当阻塞比为0.3、真空度为0.01atm、运行速度为1 000 km/h时，列车周围温度分布及列车尾部管道温度分布见图3、图4。

磁悬浮列车以较高速度通过低真空管道的过程中，由于车上设备发热，列车作为热源向低真空管道环境传热，管壁绝热，管道内静止流体以相对于列车运行速度与列车表面进行对流换热，达到管道-列车系统温度的平衡。由图3、图4可知，在管道内流体与列车表面温度达到平衡时，列车前端管道内流体温度相对于初始状态有所升高，从车头至车尾管道温度降低，车尾后端区域管道内温度最低，在车尾足够远处管道温度恢复初态温度。这主要是由于在运行过程中，列车对管道内部列车前端气体产生压缩作用，气体温度升高，列车后端气体在短时间内压力降低，温度有所降低。

2.2.1 列车表面最高温度变化

当管道阻塞比为0.3时列车表面的最高温度见表2，真空度为0.01atm时列车表面的最高温度见图5。

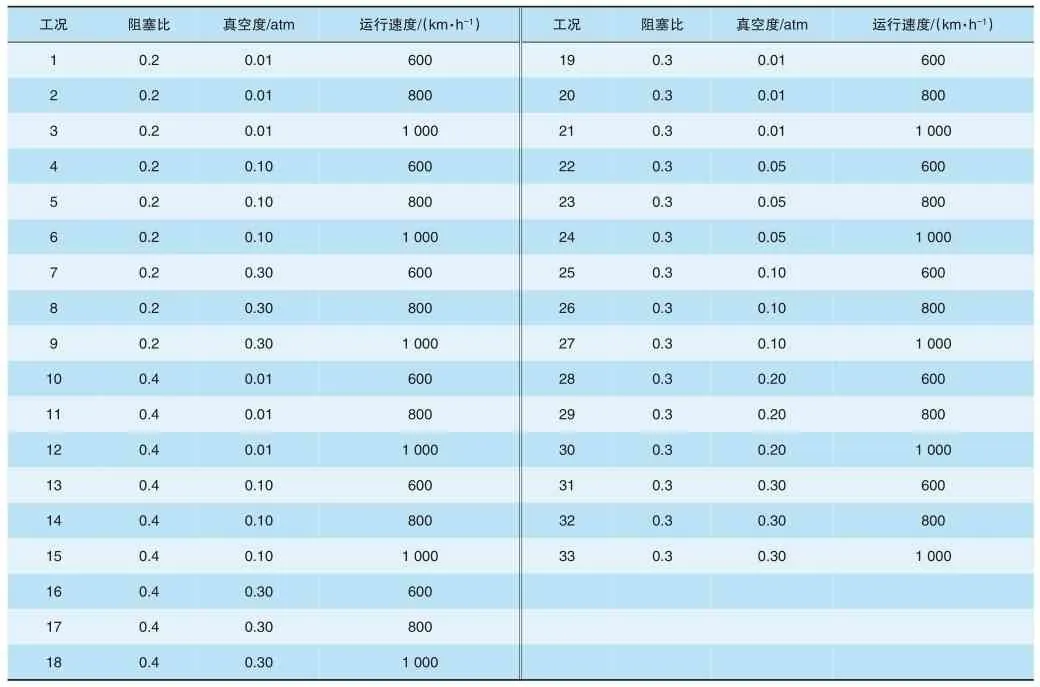
表1 仿真计算工况

图3 列车周围温度分布

由表2可知，当管道阻塞比为0.3时，列车运行速度由600 km/h提高到1 000 km/h过程中，系统达到热平衡，真空度为0.10atm、0.05atm、0.01atm的条件下列车表面最高温度分别降低约12、21、75 K。这主要是由于在不考虑管道散热和列车发热功率变化的情况下，在同一真空度及管道阻塞比条件下，列车运行速度越高，列车表面与空气的对流换热系数越大、散热性能越好，达到热平衡时列车表面的温度越低。当管道阻塞比为0.3时，真空度由0.10atm升高到0.01atm的过程中，系统达到热平衡，运行速度为600、800、1 000 km/h时列车表面最高温度分别升高约188、150、125 K。这主要是由于在不考虑管道散热和列车发热功率变化的情况下，在同一运行速度及管道阻塞比条件下，管道真空度越高，管道内空气密度越小，雷诺数越小，车体表面与空气的对流换热系数越小、散热性能越差，达到热平衡时车体表面的温度越高。

图4 列车尾部管道温度分布

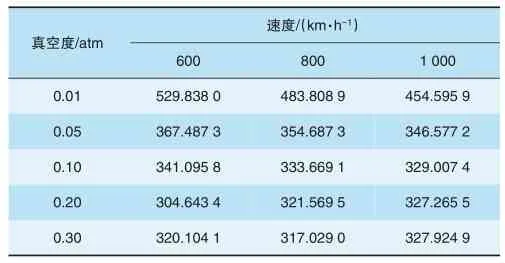
表2 管道阻塞比为0.3时列车表面的最高温度 K

图5 真空度0.01atm时列车表面最高温度

由图5可知，当真空度为0.01atm时，管道阻塞比由0.2提高到0.4的过程中，系统达到热平衡，运行速度为600、800、1 000 km/h时列车表面最高温度分别降低约35、28、23 K。这主要是由于在不考虑管道散热和列车发热功率变化的情况下，在同一运行速度及管道真空度下，阻塞比越高，管道截面积越小，强化了流体流经管道对流换热的效果，达到热平衡时车体表面的温度越低；同时，当真空度为0.01atm时，在各个运行条件下，列车表面温升均超过约140 K。

在计算的33个工况中，真空度小于0.10atm的各个工况均表现出与表2和图5相似的温度变化规律。在真空度大于0.10atm的条件下，列车表面最高温度随着运行速度和管道真空度、阻塞比的变化不明显。这主要是由于在不考虑列车发热功率变化的情况下，当列车运行速度为600～1 000 km/h、管道真空度大于0.10atm时，列车表面与空气的对流换热系数较大，散热性能较好，列车表面能够与管道内气体进行充分热交换，此时列车表面温度受运行速度、管道真空度与阻塞比的变化影响较小。

2.2.2 管道内流体温度变化

阻塞比为0.3、真空度为0.01atm、运行速度为1 000 km/h时，管道内流体温度值分布见图6；真空度为0.01atm时，管道温度与速度和阻塞比的关系见图7；阻塞比为0.3时，不同速度和真空度下的管道温度见表3。

图6 阻塞比0.3、真空度0.01atm、运行速度1 000 km/h时的管道内流体温度值分布

图7 真空度0.01atm时管道温度与速度和阻塞比的关系

由图7可知，随着阻塞比的增加，管道内列车前端高温区温度有所升高，列车后端低温区温度降低，这是由于阻塞比的增加加强了列车对管道内气体的压缩作用，列车前后端区域压强差增大，温差增大；结合图5和图7可知，当真空度为0.01atm、列车运行速度为1 000 km/h，随着阻塞比分别为0.2、0.3、0.4时，列车表面最高温度与管道内流体最高温度温差逐渐缩小，分别达到约142、126、111 K。

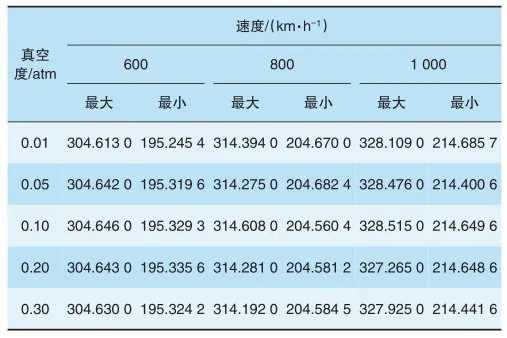
表3 阻塞比为0.3时不同速度和真空度下的管道温度K

由表3可知，管道内温度几乎不随真空度的变化而变化。当阻塞比为0.3时，列车运行速度由600 km/h升高到1 000 km/h的过程中，管道高温区温度升高约24 K，管道低温区温度升高约19 K，管道内列车前后端区域温度的升高是由于随着列车运行速度的升高，列车表面对流换热性能提高，达到热平衡时，列车表面与管道内温差缩小。

3 结论

在一定基本假设的基础上，针对部分运行工况对低真空管道磁悬浮列车的热效应进行仿真计算，得出以下结论，可为低真空管道磁悬浮列车热效应的仿真计算及理论研究提供参考。

（1）当阻塞比为0.3时，列车运行速度由600 km/h提高到1 000 km/h的过程中，管道真空度为0.10atm、0.05atm、0.01atm的运行条件对应列车表面最高温度分别降低约12、21、75 K。

（2）当阻塞比为0.3，列车运行速度为1 000 km/h时，管道真空度由0.01atm降低到0.10atm的过程中，达到热平衡时列车表面最高温度降低约125 K；当管道真空度在0.01atm～0.10atm变化时，列车表面最高温度的变化较明显。

（3）当真空度为0.01atm时，在各个运行工况下，列车表面温升均超过约140 K。

（4）当真空度为0.01atm时，阻塞比由0.2提高到0.4的过程中，运行速度为600、800、1 000 km/h对应列车表面最高温度分别降低约35、28、23 K。

（5）在列车前进方向上管道温度升高，车尾方向管道温度降低；当阻塞比为0.3时，列车运行速度由600 km/h提高到1 000 km/h的过程中，列车前后端管道温度分别升高约24 K和19 K，列车运行速度的升高使得管道温度升高。

（6）当真空度为0.01atm、列车运行速度为1 000 km/h，通过阻塞比分别为0.2、0.3、0.4的管道时，达到热平衡时的列车表面最高温度与管道内流体最高温度温差分别达到约142、126、111 K。