EXISTENCE OF UNBOUNDED SOLUTIONS FOR A n-TH ORDER BVPS WITH A p-LAPLACIAN∗†

Gaosheng Yan,Hairong Lian,Xinyu Fang,Yue Gao

(School of Science,China University of Geosciences,Beijing,100083,PR China)

Abstract

Keywords p-Laplacian;upper solutions;lower solutions;infinite interval;degree theory

1 Introduction

This paper discusses the n-th differential equation with a p-Laplacian operator on the infinite interval

with the Sturm-Liouville boundary conditions:

In recent years,the p-Laplacian boundary value problem attracted considerable attention due to their application in mechanics,astrophysics and frequent appearance in the classical electrical.The existence of the solutions,positive or multiple ones have been discussed by using the upper and lower solution method,the fixed point theory,the shooting method,the critical point theory.See[2,4,13-20]for high order boundary value problems.In[2],John R.Graef et al.considered the higher order ϕ-Laplacian BVP with the generalized Sturm-Liouville boundary condition

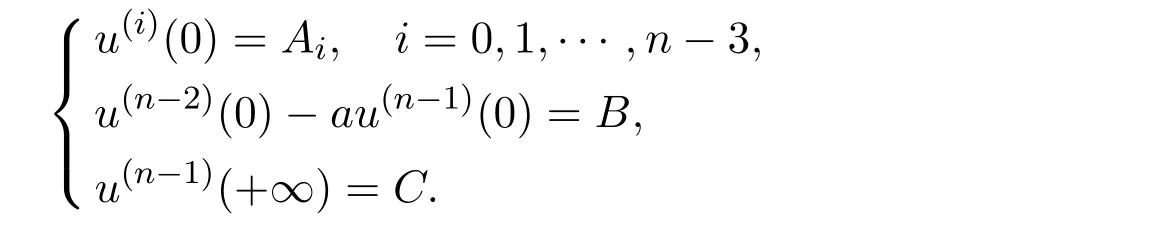
[16,17]considered even order differential equations,[14,18]studied multi-point BVPs.For differential equations with Laplace operator,some scholars have explored them on unbounded domains,but just for first or second order(see[3-8]).

Inspired by the above works,we intend to use the upper and lower solution method to solve the higher order differential equation with p-Laplacian operator on the infinite interval.Here,the compactness of the infinite interval is worth attention.We assume problem(1.1)with(1.2)exists a pair of upper and lower solutions and the nonlinear function f satisfies a Nagumo condition.Through using the truncation method and upper and lower solution method,we give a priori boundary of the truncation problem.Then the Sch¨ader fixed point theorems guarantee the existence of the solution of problem(1.1)with(1.2).On this basis,by assuming that there are two pairs of upper and lower solutions,the existence of multiple solutions is discussed.In the last part,two examples are included to illustrate the main results in this paper.This work is done to show how the method of upper and lower solution can be used to establish the existence of unbounded solutions of p-Laplacian model on an infinite interval.

2 Preliminaries

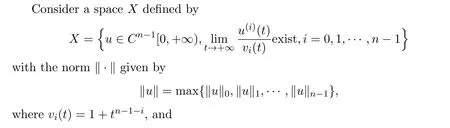
3 The Existence Results

Our existence theory is based on the theory of unbounded upper and lower solution.Here we list some assumptions for convenience.

Hence,T is continuous.

3.T:X→X is compact.

T is compact if it maps bounded subsets of X into relatively compact sets.LetΩ be any bounded subset of X,then there exist r2,M ＞0,such that,for any u∈Ω,‖u‖≤r2and|vu(t)|≤M(1+t),|v′u(t)|≤M,t∈[0,+∞).For any u∈Ω,we have

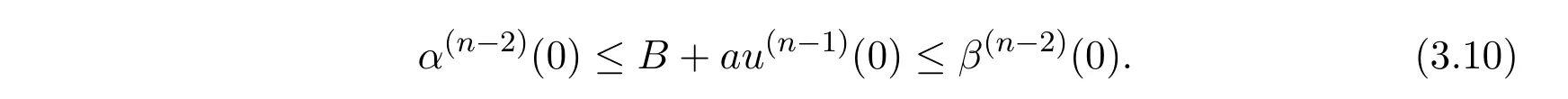
If not,we assume that

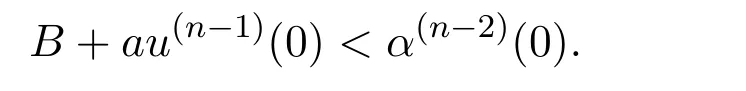
So,by(3.1),we have u(n−2)(0)= α(n−2)(0),and by(1.2),there is u(n−1)(t) ≥α(n−1)(t).Hence,

which contradicts(2.1).Thus,B+au(n−1)(0)≥ α(n−2)(0).By the same method,we can show that B+au(n−1)(0)≤ β(n−2)(0).The proof is complete.

4 The Multiplicity Results

Assuming two pairs of upper and lower solutions,we can obtain at least three solutions of such infinite interval problems.

Theorem 4.1 Suppose that the following conditions hold:

(H4)The BVP(1.1)with(1.2)has two pairs of upper and lower solutions βj,αj,j=1,2,in X,with α2,β1strict ones,and

for i=0,1,···,n−2,t∈ [0,+∞)and f ∈ C([0,+∞)×Rn,R)satisfies Nagumo condition with respect to α1and β2.

Suppose further that conditions(H2)and(H3)hold,with α and β being replaced by α1and β2.Then problem(1.1)with(1.2)has at least three solutions u1,u2and u3satisfying

Proof Define the truncated function F1the same as Fuin Theorem 3.1 with α and β being replaced by α1and β2respectively.Consider the following modified differential equation

with boundary condition(1.2).

Define a mapping T1:X→X the same as T in(3.4)except changing Futo F1.Similarly,T1is completely continuous.By using degree theorem,T1has at least three fixed points,which are the solutions of problem(4.1)with(1.2).

5 Examples