OSCILLATION OF THIRD-ORDER NONLINEAR DELAY DIFFERENTIAL EQUATIONS∗†

Jianli Yao,Xiaoping Zhang,Jiangbo Yu

(School of Science,Shandong Jianzhu University,Ji’nan 250101,Shandong,PR China)

Abstract

Keywords nonlinear differential equation;delay;third-order;oscillation

1 Introduction

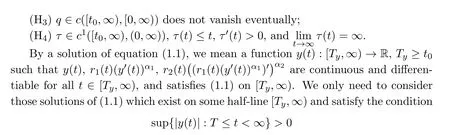
for any T≥Ty.In the sequel,we assume that(1.1)possesses such a solution.

As is customary,a solution y(t)of(1.1)is called oscillatory if it has arbitrary large zeros on[Ty,∞).Otherwise,it is called nonoscillatory.Equation(1.1)is said to be oscillatory if all its solutions oscillate.

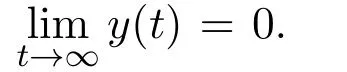
For the sake of brevity,we define the operators

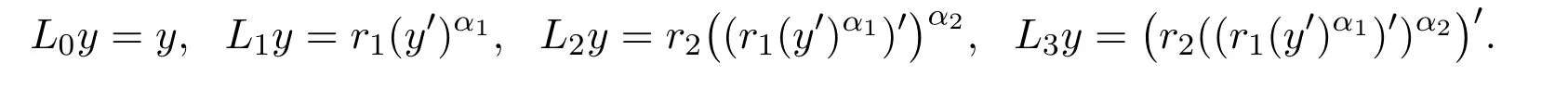
2 Main Results

As usual,all functional inequalities considered in this paper are supposed to hold eventually,that is,they are satisfied for all t large enough.

Without loss of generality,we need only to consider eventually positive solutions of(1.1).

The following lemma on the structure of possible nonoscillatory solutions of(1.1)plays a crucial role in the proofs of the main results.

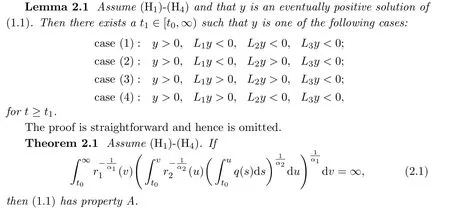
Remark 2.1 Let α1= α2=1,Theorem 2.1 is reduced to[1,Theorem 1].

Remark 2.2 It is obvious that any nonoscillatory solution in Theorem 2.1 satisfies either case(1)or case(2)in Lemma 2.1.

Next,we formulate some additional information about the monotonicity of solutions that satisfy case(2).

Lemma 2.2 Assume(H1)-(H4).Let y satisfy case(2)in Lemma 2.1 on[t1,∞)for some t1≥t0,and define a function

Setting u=τ(t)in(2.20),we get a contradiction with(2.16).

Finally,by noting that(2.1)is necessary for the validity of(2.15),it follows immediately from Remark 2.2 that cases(3)and(4)are impossible.The proof is complete.

Remark 2.4 Let α1= α2=1,Theorem 2.2 is reduced to[1,Theorem 2].

The following result is a simple consequence of Theorem 2.2 and Corollary 2.1.

Theorem 2.3 Assume(H1)-(H4).If α1α2=1,(2.10)and(2.15)hold,then all positive solutions of(1.1)satisfy(2.14)for any k＞0 and t large enough.

Next,we provide a result which can serve as alternatives to Theorem 2.2.

Taking limsup on both sides of the above inequality,we get a contradiction with(2.21).

We repeat the same steps as those of case(2).To show that cases(3)and(4)are impossible,it is sufficient to note that(2.2)is necessary for the validity of(2.21).The rest of proof proceeds in the same manner as that of Theorem 2.1.The proof is complete.

Remark 2.5 Let α1= α2=1,Theorem 2.4 is reduced to[1,Theorem 4].

Example 2.1 Consider the third-order delay differential equation

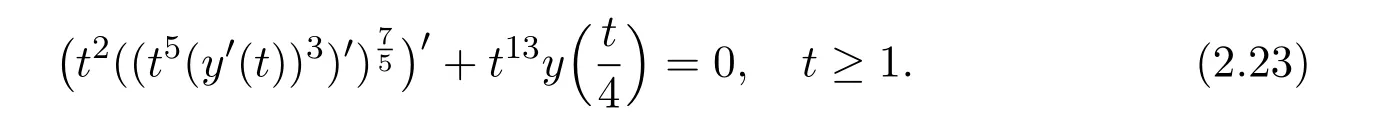
It is easy to verify that the condition(2.1)is satisfied.Using Theorem 2.1,we obtain that equation(2.23)has property A.

Example 2.2 Consider the third-order delay differential equation

respectively.Using Theorem 2.2,equation(2.24)is oscillatory if both(2.25)and(2.26)hold.

Acknowledgements The authors would like to express their highly appreciation to the reviewers for their valuable suggestions.