末端防空作战基于不同配置形式的兵力需求模型研究∗

（国防大学联合作战学院 石家庄 050051）

1 引言

高射炮兵兵力结构和规模是要地防空作战的客观物质条件，也是高射炮兵防空作战部署的主体。没有一定结构和规模的兵力，就不可能建立起与空袭斗争相适应的防空作战部署［1］。末端防空作战高射炮兵兵力需求研究涉及的因素多，许多因素具有不确定性，研究的难度大。对此，本文运用现代防空作战理论并结合可信性理论和不确定规划方法研究高射炮兵在不同配置形式下兵力需求问题，所得模型对指导防空作战具有重大现实意义。

2 高射炮兵战斗的配置形式

高射炮兵战斗的配置形式，必须有适应来袭方多方向攻击的全方位抗击能力。在兵力允许的条件下，应尽可能实施环形配置，使兵力在各方向的火力相互衔接，即使是在兵力较少无法形成环形配置时，也要合理部署，以提高防空火力纵深或火力密度［2～3］。高射炮兵战斗配置的形式通常分为四种:有重点的环形配置、扇形配置、集团配置、线形配置。

2.1 有重点的环形配置

高射炮兵有重点的环形配置，就是突出敌空袭兵器的主要来袭方向和重点目标，部队（分队）概略呈环形的配置在防空区的外围。

2.2 扇形配置

扇形配置是在主要方向上，将各阵地呈扇状进行构筑和配置。扇形配置通常是在阵地个数不够、受地形条件限制不能形成环形配置时采用。扇面角的大小，要根据要地指挥员规定的责任射界、兵力的数量、被掩护目标的分布和地形条件而定。

2.3 集团部署

集团部署是将阵地以较小的间隔距离集中配置于某一地域。部署时，相邻阵地的最小间隔，应保证各阵地电磁互不干扰及兵器发射时不危及友邻阵地的安全。集团部署的优点是防空效率高，缺点是在兵力使用上不够经济。

2.4 线形配置

线形配置是指将阵地沿保卫目标成一线构筑。线形配置很少采用，通常是在保卫特殊目标时采用。

3 分析与建模思路

防空作战高射炮兵兵力需求涉及到两个方面:一是兵力结构；一是兵力规模［4］。这两方面的研究，都是建立在高射炮兵兵力需求的基本原则、基本要求及基本依据的基础上的。对兵力结构的研究主要从定性角度进行了分析，指出在末端防御作战中应该怎样分析高射炮兵兵力结构。高射炮兵兵力规模集中在对数量的计算上，对于数量的计算大都通过定量进行研究，并建立相应的模型［5］。通过模型的解算可以得出比定性分析更加合理的结果。在具体分析中，可以把模型分为两类:一是基于环（扇）形部署的兵力规模需求计算模型；一是基于集团部署的兵力规模需求计算模型。建立模型中遵从这样的步骤:一是研究来袭目标攻击线路及来袭特点；二是根据实际对抗作战中一些参量（如空袭兵器的速度、高度，我方兵器距保卫目标的距离、兵器间配置间隔等）的特点，计算需要满足的相关制约条件；三是推导并建立末端防空作战高射炮兵兵力需求模型，并指出模型在实战中如何应用。

4 基于不同配置形式的兵力规模需求模型

4.1 基于环（扇）形配置的兵力需求模型

从战术原则讲，环形配置与扇形配置是有区别的，在兵力规模需求计算中环形配置能够达到最好的防空效果［6～7］。实际作战中由于受到兵力数量、地形等因素的制约，环形配置形式在部署时受到一定的限制，因此考虑扇形配置。高射炮兵在要地防空作战中负责末端防御层的防护任务，在上级规定的方向上进行部署，以扇形为要。如图1，实际建立模型中两种配置形式在于敌空袭区域张角α在大小上的区别，当α成一定角度时环形配置就可以看作扇形配置来研究。以扇形配置形式为例建立模型。

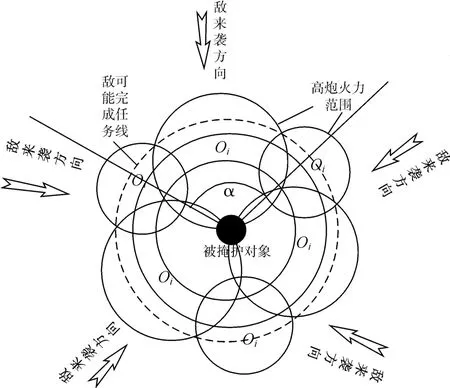
图1 单层环形配置

4.1.1 单层配置兵力规模需求的确定性模型

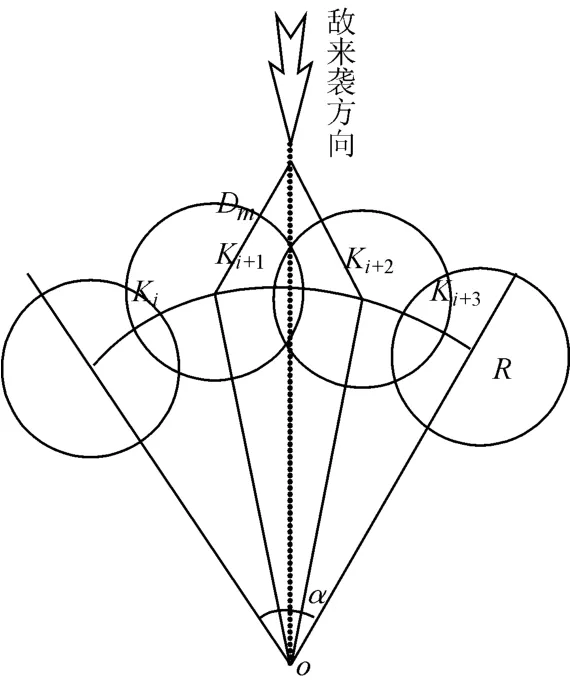
图2 单层扇形配置

如图2，空袭目标沿两火力单位之间的中线对保卫目标实施攻击。X个火力单位K1、K2、…、Kx单层呈扇形均匀配置，为保证四个火力单位都能对同一目标实施射击，需满足:

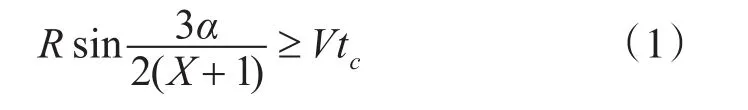
式中:X为火力单位数量；R距保卫目标距离；α空袭区域张角；V空袭目标飞行速度；tc最小射击周期。

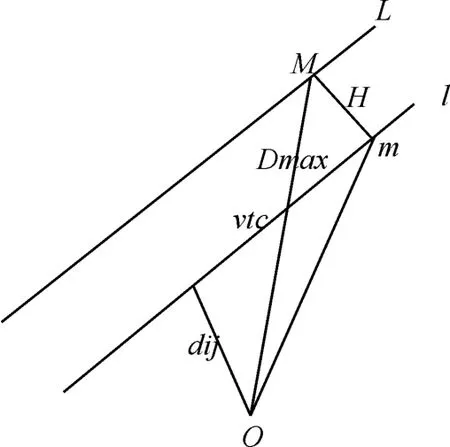
图3 兵力需求计算立体图

如图2、图3所示高炮的水平杀伤距离与“保证四个火力单位能对同一目标实施射击需满足的条件”之间的几何关系，可以得到:

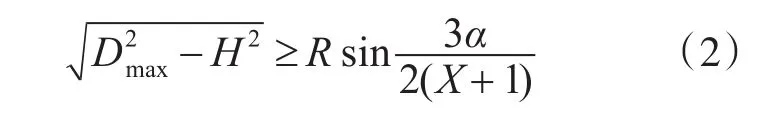
式中:Dmax为高炮的杀伤远界；H为空袭目标飞行高度。

由图2，图3可以得到含有火力单位数量X的目标航路捷径之间的关系式:

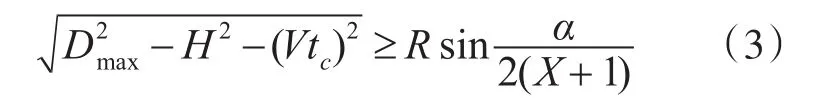
式子中的参数与上述参数相同。在图2中根据战术原则［8］，相邻的火力单元之间的距离需满足以下条件:

式中:r为火力单位之间的配置间隔。

在来袭方向上，空袭目标在通过Ki+1、Ki+2火力范围的路径长度为

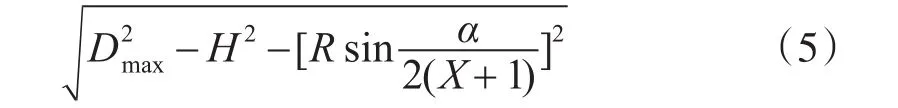
通过Ki、Ki+3火力范围的路径长度为

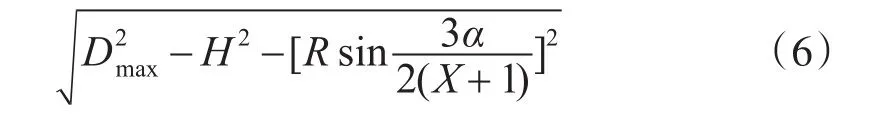
可以得到，Ki+1、Ki+2对空袭目标的射击次数为

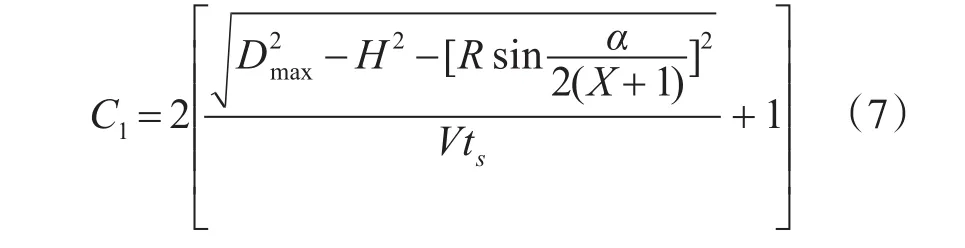
式中:ts为火力单位的射击周期。

Ki、Ki+3对空袭目标的射击次数为

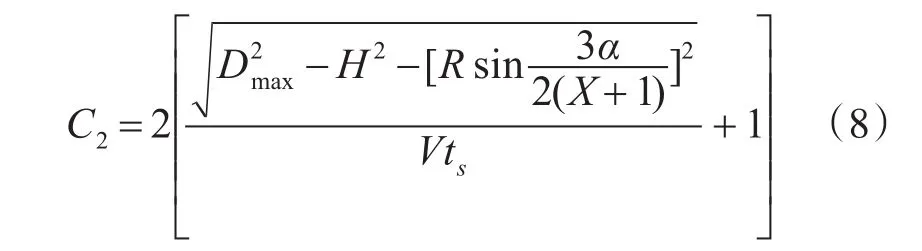
式子中参数与上述相同。

可以得到，Ki、Ki+1、Ki+2、Ki+3对空袭目标的射击总次数为

火力单位呈扇形均匀配置，1-(1-p)C（p为单个火力单元对空袭目标一次射击的毁伤概率）为空袭目标完成任务前被毁伤概率，其值当然越大越好，令:

根据以上各式可以求出X的关系式，结合攻防双方实际对抗情况，得出基于单层配置的兵力规模需求模型:

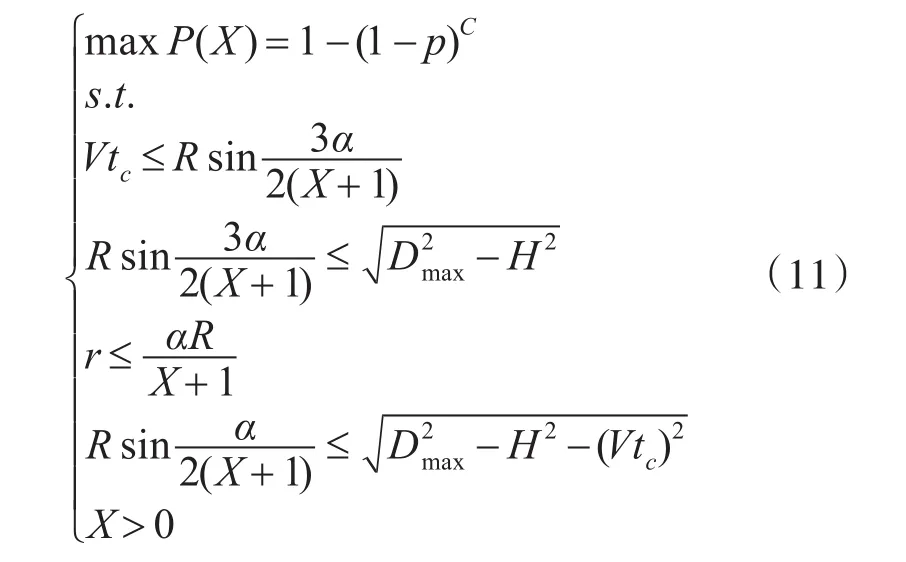
4.1.2 双层配置兵力规模需求模型

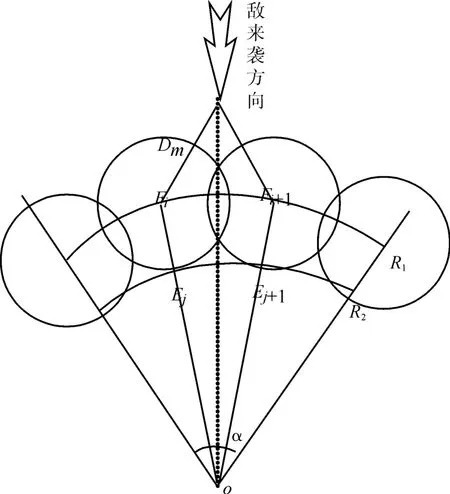
图4 双层扇形配置

双层配置时，外层数量为x1，配置在距保卫目标为R1的扇形R上，内层数量为x2，配置在距保卫目标为R2的扇形上，并希望每层各有两个火力单位可同时实施射击。空袭目标沿两火力单位之间的中线对保卫目标实施攻击［9］。

如图4，火力单位呈双层防线配置时，外层有F1、F2、…、Fx1，x1个火力单位。内层有E1、个火力单位，配置半径分别为R1和R2（R1＞R2）。同单层防线的配置分析，外层Fi、Fi+1对空袭目标的射击次数为

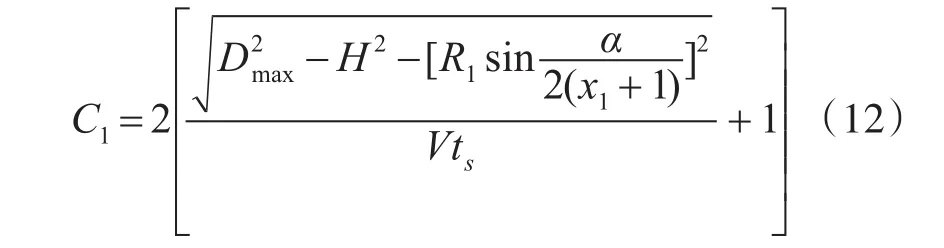
式中:x1为外层火力单位数量；R1为外层距保卫目标距离；x2为内层火力单位数量；R2为内层距保卫目标距离；R1＞R2。

内层Ej、Ej+1对空袭目标的射击次数为

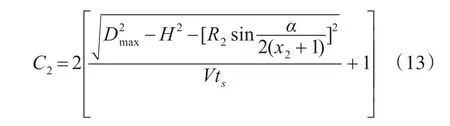
式子中参数与上述相同。

可以得到，Fi、Fi+1、Ej、Ej+1对空袭目标的射击总次数为C=C1+C2。

得到基于双层配置的兵力规模需求确定性模型:

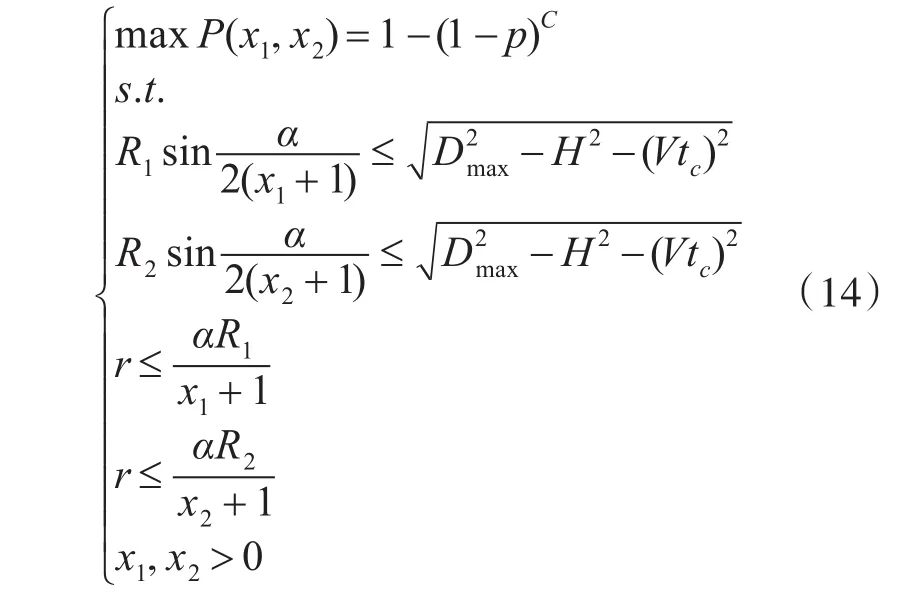
模型在实际应用过程中有一定的指导意义，当指挥员事先了解到我方对目标的毁伤概率p、配置层与保卫目标的距离R1、R2，火力单位的射击周期为ts、最小射击周期tc、高炮杀伤远界为Dmax、敌方空袭区域张角α及事先给定相应的置信水平值，在敌空袭兵器飞行高度H、速度V和我方兵器配置间隔r未知的情况下，就可以计算出作战所需双层部署的兵力规模。

4.2 基于集团配置的兵力需求模型

4.2.1 航路捷径计算

如图5所示，高炮部队对来袭目标的水平杀伤区远界半径为D，最大航路角为qmax，最大航路捷径为dj。

为有效抗击来袭目标，火力单位杀伤区必须有一定杀伤纵深［10］。水平杀伤纵深l1=|AB|的最小值可按下面方法计算。

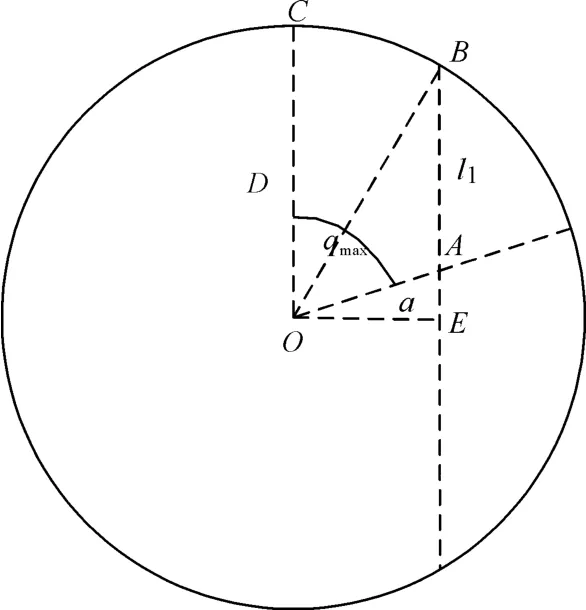
图5 有效航路捷径计算示意图

假设空战中，进行n次转火射击，转火时间Δt，则n次转火遭遇的时间间隔约为(n-1)Δt，设目标速度为V则:

4.2.2 集团配置兵力规模需求模型

要抗击具有较大来袭目标密度的目标流，或对重要目标进行集火射击，必须形成火力重叠［11］。

由图6、图7可以看出，要构成数量为X、正面宽度为L的有效射击区域，火力单位配置间隔DI满足:

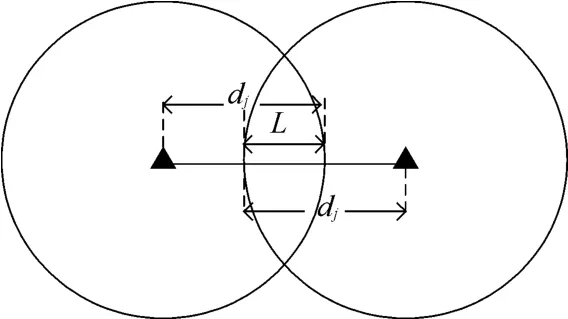
图6 火力重叠数为2时的集团配置示意图

当X=1时，DI≤2dj；

当X=2时，DI≤2dj-L，显然L≤2dj；

当X=3时，2DI≤2dj-L；

当X=n时，(n-1)DI≤2dj-L。

即构成X次重叠的最大配置间隔为

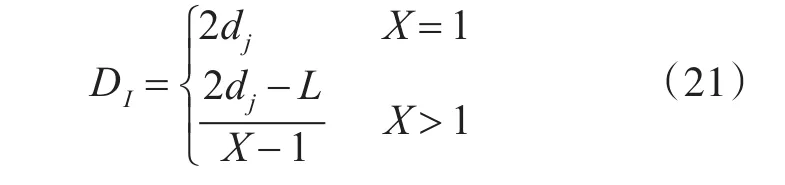
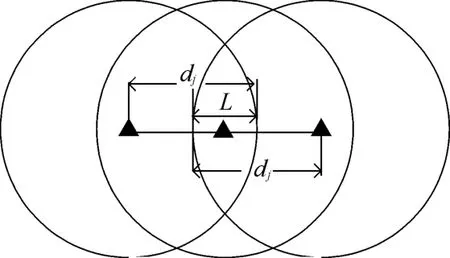
图7 火力重叠数为3时的集团配置示意图

设单个火力单位火力密度为μ，则X次火力重叠区的火力密度为Xμ。防空作战中，高炮的数量是有限的，战技性能有限，这使得防空只能对部分来袭目标进行抗击［12］。设来袭目标密度为λ，上级要求对目标的毁伤概率为P。要有效抗击空中之敌，需满足:

模型在实际应用过程中有一定的参考价值，当指挥员事先了解到高炮水平杀伤区远界半径为D，目标最大航路角为qmax，转火射击次数n，转火时间Δt，正面宽度为L及事先给定相应的置信水平值，在敌空袭兵器飞行速度V和我方兵器配置间隔r未知的情况下，就可以较合理地计算出基于集团配置形式作战所需的兵力规模。

5 结语

根据防空作战三层防御体系相关情况，高射炮兵要胜任末端防空任务，必须要有合理的兵力结构。从总体上来说，空中目标低空、超低空飞行，遇到的地空导弹射击的概率比较低，因而低空特别是超低空突防技术仍然受到空袭体系的重视。防空作战要求火力必须覆盖不同高度、不同方向，现役高炮可以有效地弥补导弹对付低空、超低空突袭的弱点。在低空、超低空火力重叠次数很少，甚至有很大的火力不能覆盖的空白区，配置不同的高炮尤为重要。本文通过构建不同配置形式下兵力需求模型，对指导末端防空作战具有一定应用价值和实践意义。